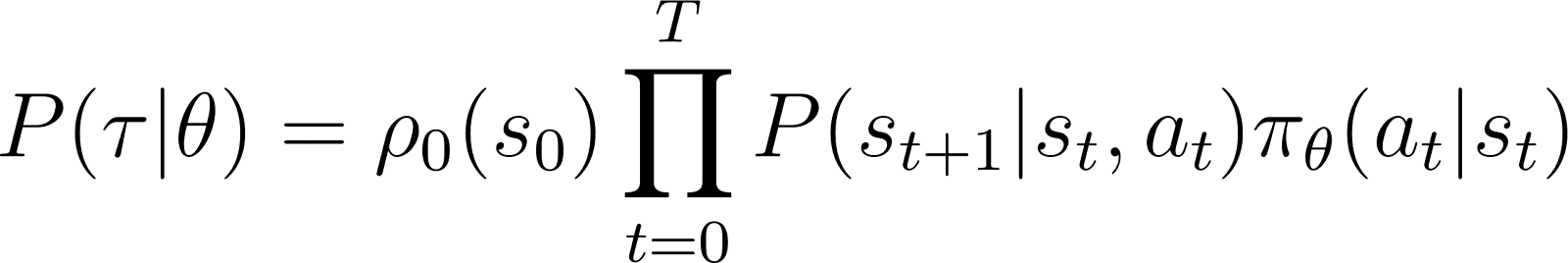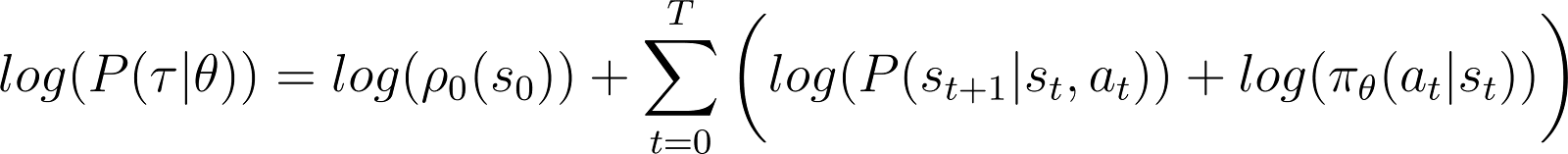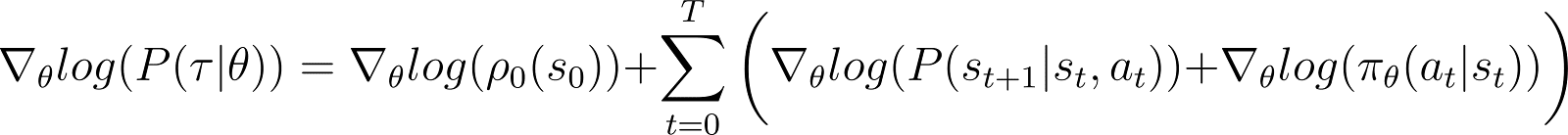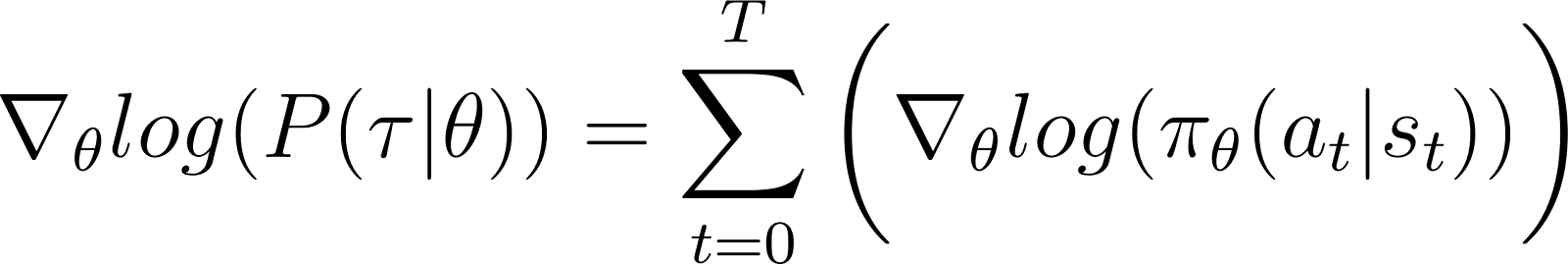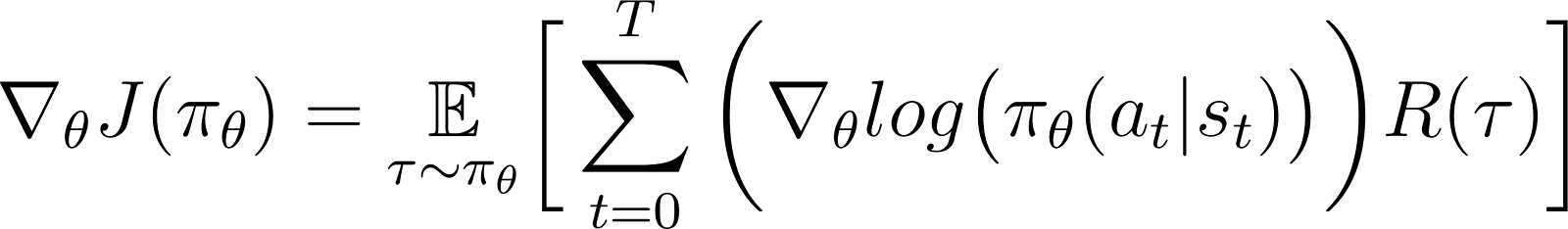政策梯度定理解析：實戰導論

為什麼使用政策梯度法？

政策梯度方法的一個關鍵優勢是它們能夠處理複雜的動作空間，傳統的基於價值的方法難以應對。

處理高維度的動作空間

基於價值的方法，如Q-learning，通過估計所有可能動作的價值函數來工作。當環境的動作空間是連續的或是離散但很大時，這變得困難。

策略梯度方法對策略進行參數化，並估計相對於該策略參數的累積獎勵的梯度。它們使用這個梯度直接優化策略，通過更新其參數。因此，它們可以有效處理高維度或連續的動作空間。策略梯度也是強化學習使用人類反饋（RLHF）方法的基礧。 使用人類反饋進行強化學習（RLHF）方法。

通過對策略進行參數化並根據梯度調整其參數，策略梯度可以有效處理連續和高維度動作。這種直接方法能夠更好地泛化和更靈活地探索，使其非常適合於機器人控制和其他複雜環境的任務。

學習隨機策略

給定一組觀察：

• 確定性策略指定了代理人採取的行動。
• 隨機策略提供一組行動以及代理人選擇每個行動的概率。

遵循隨機策略時，同一觀察結果可能導致在不同迭代中選擇不同的行動。這促進了對行動空間的探索，防止策略陷入局部最優解。因此，在探索尋找導致最大回報路徑至關重要的環境中，隨機策略非常有用。

在基於策略的方法中，將策略輸出轉換為概率分佈，每個可能的行動被分配一個概率。代理人通過對該分佈進行抽樣來選擇行動，從而實現了隨機策略。因此，策略梯度方法結合了探索和利用，在具有複雜獎勵結構的環境中非常有用。

政策梯度定理的推導

在深入推导之前，建立数学符号和证明过程中使用的关键概念非常重要。

数学符号和基础知识

正如前面的部分所述，策略梯度定理指出预期回报的导数是回报和策略对数的导数乘积的期望。

在推导策略梯度定理之前，我们引入以下符号：

• E[X]表示随机变量X的概率期望。
• 從數學上來說，政策被表達為一個概率矩陣，根據不同的觀察給出選擇不同行動的概率。政策通常被建模為一個帶有參數的函數，其中參數表示為θ。
• π_θ 指的是由θ参数化的政策。在实践中，这些参数是模拟政策的神经网络的权重。
• 軌跡τ指的是一系列狀態，通常從隨機初始狀態開始，直到當前時間步或終端狀態。
• ∇_θf 指的是對於參數 f 的梯度θ。
• J(πθ) 指的是代理根据策略 π_θ 所实现的预期回报。这也是梯度上升的目标函数。
• 環境在每個時間步驟根據代理的動作給予獎勵。回報是從初始狀態到當前時間步驟的累積獎勵。
• R(τ) 指的是在轨迹τ上生成的回报。

導出步驟

我們展示如何從第一原理開始推導並證明政策梯度定理，從擴展的目標函數出發，並使用對數導數技巧。

目標函數（方程式1）

政策梯度方法中的目標函數是回報

J根據政策π 的軌跡進行累積，並以參數θ表示。這個目標函數如下：

在上述方程中：

• 左侧（LHS）是按照政策π_θ实现的预期回报。
• 右手邊（RHS）是根據沿著政策τ 生成的軌跡期望的期望（在每個步驟上）π_θ的回報R(τ)是在軌跡τ上生成的。

目標函數的微分（方程2）

對上述方程的兩側進行微分（關於θ）得：

期望的梯度（方程3）

右側的期望可以表示為乘積的積分：

• 遵循軌跡 τ
• 在軌跡上生成的回報τ

因此，方程式2的右手邊被重新表述為：

積分的梯度等於梯度的積分。因此，在上述表達式中，我們可以將梯度∇_θ放在積分符號下。因此，右邊變為：

因此，方程式2可以被重寫為：

軌跡的機率（方程式4）

現在我們更仔細地觀察 P(τ|θ)，代理人按照軌跡 τ 給定策略參數 θ (因此策略 π_θ)。一個軌跡由一組步驟組成。因此：

• 獲得軌跡 τ 的機率是以下各項的乘積：
• 遵循所有個別步驟的機率。

• 在時間步驟 t，代理人從狀態 s 轉移到狀態 s_t+1，採取動作 a_t 的機率是以下乘積給出的：
• 該策略預測在狀態a_t中採取行動的機率
• 在给定动作a_t和状态s_t的情况下，最终处于状态s_t+1的概率

因此，從初始狀態s₀開始，代理根據策略τ的軌跡機率如下所示：

為了讓事情變得更簡單，我們希望將上面的 RHS 產品表示為一個和。因此，我們對上面的方程式兩邊取對數：

對數概率的導數（方程式 5）

現在我們對上述方程式中的對數概率進行導數（關於 θ）。

在上述方程式的 RHS：

• 第一个术语log ρ₀（s₀）对于θ是常数。因此其导数为0。
• 求和符號內的第一項P(s_t+1|s_t, a_t) 也與 θ 及其對於 θ 的導數也為0。

從方程式中刪除上述的零項，我們得到（方程式5）：

回想一下方程式2：

方程式5評估了方程式2右手邊第一部分的對數。我們需要將一個項的導數與其對數關聯起來。我們使用鏈式法則和對數導數技巧來完成這一步。

對數導數技巧

我們暫時採用微積分規則來推導出一個結果，我們將使用這個結果來簡化先前的方程式，使之適合於計算方法。

在微積分中，對數的導數可以表示為：

因此，重新排列以上方程式，x的導數可以用對數的導數表示：

這有時被稱為對數導數技巧。

链规则

根據鏈式法則，給定 z(y) 作為 y 的函數，其中 y 本身是 θ 的函數， y(θ)，對於 z 關於 θ 的導數如下所示：

在這種情況下，y(θ)代表P(θ)並且z(y)代表log(y)。因此，

應用鏈規則

我們從微積分知道，d(log(y)) / dy = 1/y。將此應用在上述右手邊的第一個表達式中。

將 y 移至左手邊並使用 標記：

y代表P(θ)。因此，上述方程等同於：

應用對數導數技巧

上述結果給出了方程2 RHS 的第一個表達式（如下所示）。

使用方程2 RHS 中的結果，我們得到：

我們將 RHS 積分下的項重新排列如下：

推導最終結果

觀察上述表達式中包含期望值的積分展開： ∫P(θ)∇logP(θ) = E[∇logP(θ)]

因此，上述的RHS可以被表达为期望值：

我们在期望回报的表达式中替换对数概率的导数：

在上述方程中，將∇的值代入從方程5中得到的logP(θ)，得到：

這是根據策略梯度定理的獎勵函數的梯度表達式。

策略梯度的直覺

策略梯度方法將策略的輸出轉換為概率分佈。代理從這個分佈中進行抽樣以選擇行動。策略梯度方法會調整策略參數。這導致在每次迭代中更新這個概率分佈。更新後的概率分佈在選擇導致更高獎勵的行動時具有更高的可能性。

策略梯度算法計算期望回報對策略參數的梯度。通過朝著這個梯度的方向移動策略參數，代理在訓練過程中增加選擇導致更高獎勵的行動的概率。

本質上，導致更好結果的行動在未來變得更有可能被選擇，逐步改善策略以最大化長期獎勵。

在Python中實現策略梯度

在討論了政策梯度的基本原則後，我們將展示如何使用 PyTorch 和 Gymnasium 來實現它們。

建立環境

作為第一步，我們需要安裝 gymnasium 以及一些支持庫，如 NumPy 和 PyTorch。

要在服務器或本地機器上安裝 gymnasium 及其依賴項，運行：

$ pip install gymnasium 

要在 Google Colab 或 DataLab 等 Notebook 中安裝，請使用：

!pip install gymnasium

您可以在 Python 環境中導入這些套件：

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

編寫簡單的政策梯度代理程式

使用.make()方法來創建環境的一個實例。

env = gym.make('CartPole-v1')

和其他機器學習方法一樣，我們使用神經網絡來實現策略梯度代理。

CartPole-v1是一個簡單的環境，所以我們設計了一個只有1個隱藏層且有64個神經元的簡單網絡。輸入層的維度等於觀察空間的維度。輸出層的維度等於環境動作空間的大小。因此，策略網絡將觀察到的狀態映射到動作。給定輸入的觀察，網絡根據策略輸出預測的動作。

下面的代碼實現了策略網絡：

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

訓練代理

環境在每個時間步根據代理的狀態和動作給予獎勵。策略梯度方法包括對累積獎勵（回報）運行梯度下降。目標是最大化總回報。

為了計算一個回合中的回報，您需要對該回合中的所有時間步驟的獎勵進行累計（使用折扣因子）。此外，對回報進行歸一化有助於確保平滑穩定的訓練。下面的代碼展示了如何實現這一點：

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

在每次前向传递的迭代中，我们执行以下步骤：

• 运行代理根据当前策略使用.step()函数。策略预测在每个时间步长中采取所选择行动的概率。
• 根据代理的行动从环境中接收奖励。
• 累积步骤奖励和行动的对数概率，直到代理达到终止状态。

以下代码实现了前向传递：

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

使用反向传播和梯度上升来更新策略

在传统机器学习中：

• 损失是指预测值和实际输出之间的差异。
• 我们使用梯度下降来最小化损失。

在RL：

• 損失是梯度下降（或上升）應用的數量代理。
• 我們使用梯度上升來最大化回報（累積獎勵）。
• 預期回報值被用作梯度下降的損失代理。預期回報值是以下兩者的乘積：
• 從每個步驟預期的回報與
• 在每個步驟中選擇抽樣動作的概率。
• 為了應用使用反向傳播的梯度上升，我們使用損失的負值。

下面的程式碼計算損失：

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

與標準機器學習算法類似，為了更新策略，您運行與損失函數相關的反向傳播。下面的update_policy()方法調用calculate_loss()方法。然後對此損失運行反向傳播以更新策略參數，即策略網絡的模型權重。

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

訓練迴圈

我們使用之前定義的函數來訓練策略。在開始訓練之前，我們需要：

• 作為 PolicyNetwork 類的隨機實例初始化的未訓練策略。
• 使用 Adam 算法的優化器。
• 折扣因子、學習率、輸出率、獎勵閾值和最大訓練時期的超參數。

我們通過訓練循環迭代，直到平均回報超過獎勵閾值。在每次迭代中，執行以下步驟：

• 對於每一個情節，運行一次正向傳遞。收集動作的對數概率、逐步回報和該情節的總回報。在一個數組中累積情節回報。
• 使用對數概率和逐步回報計算損失。對損失進行反向傳播。使用優化器更新策略參數。
• 檢查超過 N_TRIALS 的平均回報是否超過獎勵閾值。

下面的代碼實現了這些步驟：

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

通過調用 main() 函數運行訓練程序：

main()

此 DataLab 工作簿 包含了政策梯度算法的上述實現。您可以直接運行它，或將其用作修改算法的起點。

政策梯度方法的優勢和挑戰

政策梯度方法具有幾個優勢，例如：

• 處理連續動作空間：基於值的方法（如 Q-learning）在連續動作空間中效率低下，因為它們需要估計整個動作空間的值。策略梯度方法可以直接使用預期回報的梯度來優化策略。這種方法在連續動作分布中表現良好。因此，策略梯度方法適用於基於連續動作空間的任務，如機器人控制。
• 隨機策略：策略梯度方法可以學習隨機策略-它給出選擇每個可能動作的概率。這使代理可以嘗試各種動作，降低陷入局部最優解的風險。這有助於在複雜環境中，代理需要探索動作空間以找到最優策略。隨機性有助於平衡探索（嘗試新動作）和利用（選擇最佳已知動作），這對於存在不確定性或稀疏獎勵的環境至關重要。
• 直接策略優化：策略梯度直接優化策略，而不使用值函數。在連續或高維度動作空間中，為每個動作近似值可能變得計算昂貴。因此，在這樣的環境中，基於策略的方法表現良好。

儘管具有許多優點，策略梯度方法也存在一些固有挑戰：

• 梯度估計的高變異性：政策梯度方法通過對概率分佈進行抽樣來選擇動作。實際上，它們對軌跡進行抽樣以估計預期回報。由於抽樣過程本質上是隨機的，後續迭代中估計的回報可能具有很高的變異性。這可能會使代理很難有效學習，因為在迭代之間政策的更新可能會出現顯著波動。
• 訓練過程中的不穩定性：
• 政策梯度方法對超參數（如學習率）敏感。如果學習率太高，則對政策參數的更新可能會太大，導致訓練錯過最優參數。另一方面，如果學習率太小，則收斂速度會很慢。
• 策略梯度方法需要平衡探索和利用。如果代理不夠探索，可能無法達到最優策略的鄰近區域。相反，如果探索過多，將無法收斂到最優策略並在動作空間周圍震盪。
• 樣本效率: 策略梯度方法通過實施每個策略直至終止並累積每個步驟中的獎勵來估計回報。因此，它們需要與環境進行許多交互作用，以獲得大量的樣本軌跡。對於狀態或動作空間較大的環境而言，這是低效且昂貴的。

穩定性解決方案

由於不穩定性是策略梯度方法中比較常見的問題，開發者已經採用各種解決方案來穩定訓練過程。以下，我們介紹使用策略梯度來穩定訓練的常見解決方案：

使用基線函數

由於採樣效率低下，在訓練迭代過程中估計的回報梯度可能存在高變異性，使得訓練不穩定且緩慢。減少變異性的一種常見方法是使用基準函數，例如優勢行動者-評論者（A2C）方法。其概念是使用代理（優勢函數）來替代估計回報作為目標函數。

優勢是通過計算從抽樣軌跡獲得的實際回報與給定初始狀態的預期回報之間的差異來計算的。此方法涉及使用值函數作為狀態和狀態-行動對的預期值。通過將損失表示為實際回報與預期回報之間的差異而不是僅作為回報，A2C減少了損失函數中的變異性，從而減少了梯度的變化，使訓練更穩定。

使用熵正則化

在某些環境中，例如僅有極少狀態會給出獎勵的環境中，策略很快會採用一種確定性方法。它還會採取貪婪方法並利用已經探索過的路徑。這將阻止進一步的探索並通常導致收斂到局部最優解和次優策略。

解決方案是鼓勵探索，對於當政策變得過於確定時進行懲罰。這是通過向目標函數中添加基於熵的項來實現的。熵測量政策中的隨機性。熵越大，代理選擇的行動中的隨機性就越多。這個基於熵的項是熵係數與當前政策的熵的乘積。

將熵納入目標函數有助於在開發和探索之間達成平衡。

政策梯度擴展

在各種政策梯度方法的擴展中，最基本的之一是REINFORCE算法。它提供了政策梯度定理的直接實現，並且是更先進技術的基礎。

REINFORCE算法

REINFORCE算法，也被稱為蒙特卡羅Reinforce，是政策梯度定理的基本實現之一。它使用蒙特卡羅方法來估計回報和政策梯度。當遵循REINFORCE算法時，代理直接從環境中對所有動作（從初始到終端狀態）進行抽樣。這與其他方法（如TD-Learning和動態規劃）形成對比，後者根據值函數估計來啟動其動作。

以下，我們介紹REINFORCE算法的基本步驟：

• 使用隨機參數初始化策略
• 重複多個訓練周期。對於每個周期：
• 生成整個周期的每個步驟如下：
• 將狀態傳遞給策略函數。
• 政策函數為每個可能的動作生成概率。
• 從這個概率分佈中隨機抽樣一個動作。
• 對於每個情節中的狀態，估算直到步驟的回報（折扣累積獎勵）。
• 估算目標函數的梯度（根據政策梯度定理），表示為每個步驟的逐步回報和動作概率的乘積。
• 通過應用梯度來更新政策參數

對於每個策略，您可以採樣單個軌跡來估計梯度（如上所示），或者對在相同策略下採樣的多個軌跡的梯度進行平均。

演員-評論方法

演員-評論方法將策略梯度方法（如REINFORCE）與值函數相結合。

• 演員的工作方式與策略梯度方法類似。演員實施策略，在每個步驟基於該策略選擇行動。它通過遵循預期回報的梯度來更新策略。
• 評論實現值函數，該值函數用作基準（在上一節中討論）。這有助於使訓練更有效和穩定。

政策梯度方法如REINFORCE使用原始回報估計沿著每條軌跡的梯度。由於取樣過程繪製這些軌跡，可能導致回報和梯度的巨大變異。使用優勢函數代替原始回報可以解決這個問題。優勢函數是實際回報和預期回報（即價值函數）之間的差異。演員-評論者方法是一類算法。當評論者使用優勢函數實現時（最常見的方法），這也被稱為優勢演員-評論者（A2C）。

Proximal Policy Optimization（PPO）

在複雜環境中，像A2C這樣的演員-評論者方法本身不足以控制回報和梯度的變異。在這種情況下，人為地限制每次迭代中策略更改的幅度有助於解決問題。這迫使更新後的（梯度上升後的）策略保持在舊策略的附近。

像Proximal Policy Optimization這樣的方法對政策梯度進行了兩個修改：

• 使用優勢函數。通常，此優勢函數以值函數作為基準。在這方面，它們類似於A2C方法。
• 限制每次迭代中策略參數可變動的量。這是通過使用修剪的替代目標函數來實現的。該算法指定了新策略與舊策略之間比率必須位於的範圍。當比率（經過梯度更新後）超出這些預定值時，會被修剪為位於範圍內。

因此，PPO顯著改善了基本策略梯度方法，在複雜環境中提高了穩定性。修剪的目標函數防止了回報和梯度中的大變異對策略更新造成不穩定性。為了在探索和利用之間取得平衡，也可以修改PPO以使用熵正則化。方法是將一個熵項（一個乘以策略熵的縮放參數）添加到目標函數中。

最近的進展

政策梯度是用來解決RL問題的最早方法之一。在快速GPU問世後，各種新方法已被提出，應用現代ML技術到政策梯度中。

梯度提升強化學習

近年來，在RL算法中應用諸如梯度提升的方法取得了進展。梯度提升將多個弱模型的預測結合起來生成一個強模型。這被稱為梯度提升強化學習（GBRL）。GBRL是一個類似於XGBoost的Python軟件包，用於實現這些技術應用於RL算法。

轉移強化學習

轉移學習（TL）是一種技術，其中一個模型獲得的知識應用於改進另一個模型的性能。轉移學習有助於解決因從頭開始訓練ML模型而導致的昂貴問題。TL方法已與策略梯度一起使用來改進RL模型的性能。這種方法被稱為轉移強化學習（TRL）。

結論

政策梯度是解決強化學習問題的最基本方法之一。

在本文中，我們介紹了政策梯度的第一原則，展示了如何推導政策梯度定理。我們還演示了如何在Gymnasium環境中使用PyTorch實現一個簡單的基於梯度的算法。最後，我們討論了基本政策梯度算法的實際挑戰和常見擴展。

如果您想加深對強化學習和使用PyTorch進行深度學習的理解，請查看這些課程：

• 強化學習專題 – 學習從基於價值的方法到政策優化技術的強化學習基礎。
• PyTorch深度學習入門 – 通過PyTorch進行實踐，從頭開始構建深度學習模型。