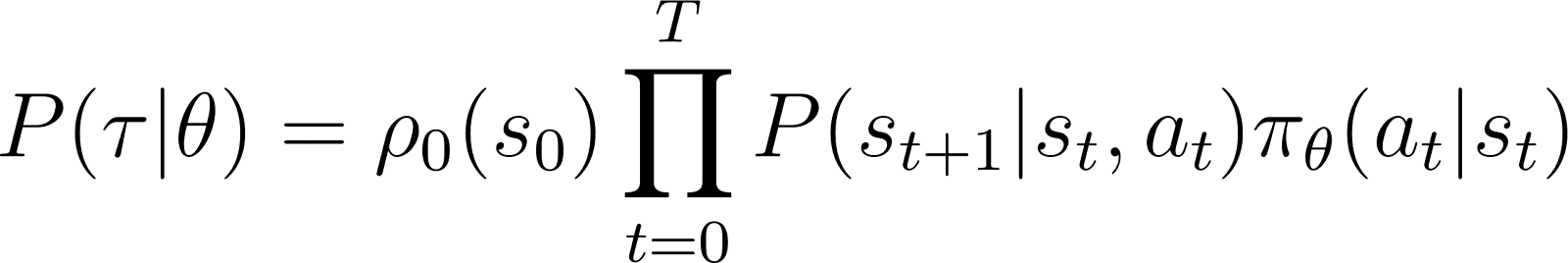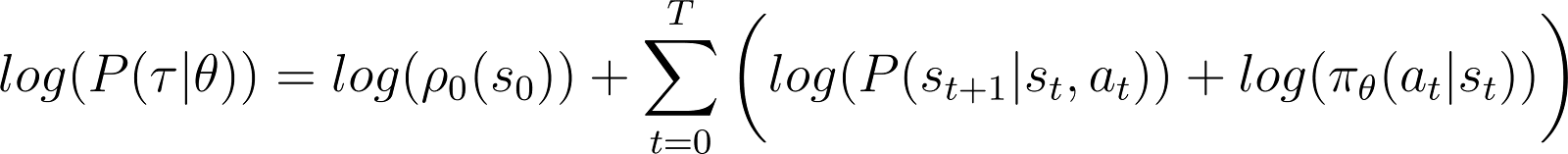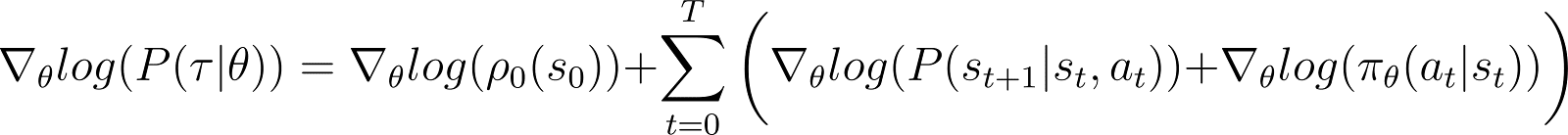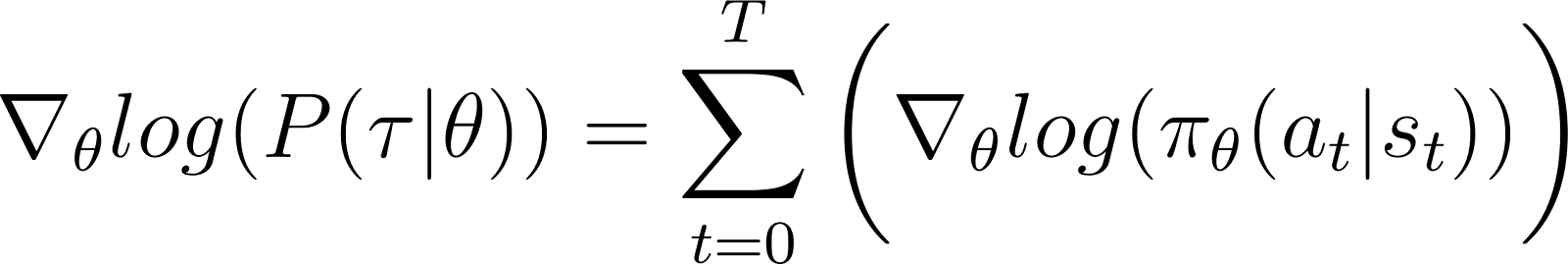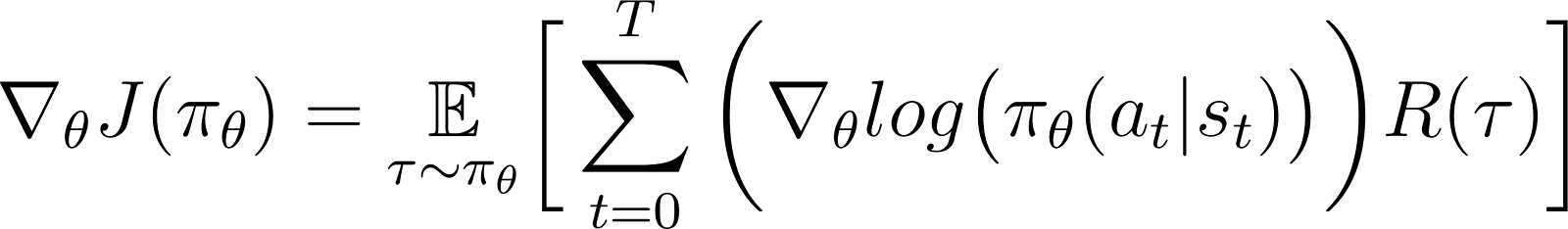Teorema del Gradiente de Política Explicado: Una Introducción Práctica

¿Por qué usar métodos de gradiente de política?

Una ventaja clave de los métodos de gradiente de política es su capacidad para manejar espacios de acción complejos, donde los enfoques tradicionales basados en valor tienen dificultades.

El manejo de espacios de acción de alta dimensión

Los métodos basados en el valor, como el Q-learning, funcionan estimando la función de valor para todas las acciones posibles. Esto se vuelve difícil cuando el espacio de acciones del entorno es continuo o discreto pero grande.

Los métodos de gradiente de política parametrizan la política y estiman el gradiente de las recompensas acumuladas con respecto a los parámetros de la política. Utilizan este gradiente para optimizar directamente la política actualizando sus parámetros. Por lo tanto, pueden manejar de manera eficiente espacios de acción de alta dimensión o continuos. Los gradientes de política también son la base de Aprendizaje por Refuerzo utilizando Retroalimentación Humana (RLHF) métodos.

Al parametrizar la política y ajustar sus parámetros en función de los gradientes, los gradientes de política pueden manejar de manera eficiente acciones continuas y de alta dimensión. Este enfoque directo permite una mejor generalización y una exploración más flexible, lo que lo hace adecuado para tareas como el control robótico y otros entornos complejos.

Aprendiendo políticas estocásticas

Dado un conjunto de observaciones:

• Una política determinista especifica qué acción toma el agente.
• Una política estocástica proporciona un conjunto de acciones y la probabilidad de que el agente elija cada acción.

Cuando se sigue una política estocástica, la misma observación puede llevar a elegir diferentes acciones en diferentes iteraciones. Esto promueve la exploración del espacio de acciones y evita que la política quede atrapada en óptimos locales. Debido a esto, las políticas estocásticas son útiles en entornos donde la exploración es esencial para descubrir el camino que conduce a los máximos rendimientos.

En los métodos basados en políticas, la salida de la política se convierte en una distribución de probabilidad, con cada posible acción asignada una probabilidad. El agente elige una acción muestreando esta distribución, lo que hace posible implementar una política estocástica. Por lo tanto, los métodos de gradiente de política combinan la exploración con la explotación, siendo útiles en entornos con estructuras de recompensa complejas.

Derivación del Teorema del Gradiente de Política

Antes de adentrarnos en la derivación, es importante establecer la notación matemática y los conceptos clave utilizados a lo largo de la demostración.

Notación matemática y preliminares

Como se mencionó en una sección anterior, el teorema del gradiente de la política establece que la derivada del retorno esperado es la esperanza del producto del retorno y la derivada del logaritmo de la política. 

Antes de derivar el teorema del gradiente de la política, introducimos la notación:

• E[X] se refiere a la esperanza probabilística de una variable aleatoria X. 
• Matemáticamente, la política se expresa como una matriz de probabilidad que proporciona la probabilidad de elegir diferentes acciones en función de diferentes observaciones. Una política suele modelarse como una función parametrizada, con los parámetros representados como θ.
• π_θ se refiere a una política parametrizada por θ. En la práctica, estos parámetros son los pesos de la red neuronal que modela la política.
• La trayectoria, τ, se refiere a una secuencia de estados, generalmente comenzando desde un estado inicial aleatorio hasta el paso de tiempo actual o el estado terminal.
• ∇_θf se refiere al gradiente de una función f con respecto al(los) parámetro(s) θ. 
• J(π_θ) se refiere al rendimiento esperado logrado por el agente siguiendo la política π_θ. Esta también es la función objetivo para el ascenso de gradiente.
• El entorno otorga una recompensa en cada paso de tiempo, dependiendo de la acción del agente. El retorno se refiere a las recompensas acumuladas desde el estado inicial hasta el paso de tiempo actual.
• R(τ) se refiere al rendimiento generado a lo largo de la trayectoria τ.

Pasos de derivación

Mostramos cómo derivar y demostrar el teorema del gradiente de política desde primeros principios, comenzando con la expansión de la función objetivo y utilizando el truco del logaritmo de la derivada.

La función objetivo (Ecuación 1)

La función objetivo en el método del gradiente de política es el retorno

J acumulado siguiendo la trayectoria basada en la política π expresada en términos de parámetros θ. Esta función objetivo se expresa como:

En la ecuación anterior:

• El lado izquierdo (LHS) es el rendimiento esperado logrado al seguir la política π_θ.
• El lado derecho (RHS) es la expectativa (sobre la trayectoria τ generada siguiendo la política π_θ en cada paso) de los retornos R(τ) generados sobre la trayectoria τ.

La diferencial de la función objetivo (Ecuación 2)

Al diferenciar (con respecto a θ) ambos lados de la ecuación anterior, se obtiene:

El gradiente de la expectativa (Ecuación 3)

La expectativa (en el RHS) se puede expresar como una integral sobre el producto de:

• La probabilidad de seguir una trayectoria τ
• Los rendimientos generados a lo largo de la trayectoria τ

Por lo tanto, el RHS de la Ecuación 2 se reformula como:

El gradiente de una integral es igual a la integral del gradiente. Por lo tanto, en la expresión anterior, podemos llevar el gradiente ∇_θ bajo el signo integral. Por lo tanto, el RHS se convierte en:

Por lo tanto, la Ecuación 2 se puede reescribir como:

La probabilidad de la trayectoria (Ecuación 4)

Ahora echamos un vistazo más de cerca a P(τ|θ), la probabilidad de que el agente siga la trayectoria τ dadas los parámetros de la política θ (y por lo tanto la política π_θ). Una trayectoria consta de un conjunto de pasos. Por lo tanto:

• La probabilidad de obtener la trayectoria τ es el producto de:
• La probabilidad de seguir todos los pasos individuales.

• En el paso de tiempo t, el agente pasa del estado s al estado s_t+1 siguiendo la acción a_t. La probabilidad de que esto ocurra se da por el producto de:
• La probabilidad de que la política prediga la acción a_t en el estado s_t
• La probabilidad de terminar en el estado s_t+1 dado la acción a_t y el estado s_t

Así, comenzando desde un estado inicial s₀, la probabilidad de que el agente siga la trayectoria τ basada en la política π_θ se da como: 

Para simplificar las cosas, queremos expresar el producto en el lado derecho de arriba como una suma. Entonces, tomamos el logaritmo en ambos lados de la ecuación anterior:

La derivada de la log-probabilidad (Ecuación 5) 

Ahora tomamos la derivada (con respecto a θ) de la probabilidad logarítmica en la ecuación anterior.

En el lado derecho de la ecuación anterior: 

• El primer término log ρ₀(s₀) es constante con respecto a θ. Por lo tanto, su derivada es 0.
• El primer término dentro de la sumatoria P(s_t+1|s_t, a_t) también es independiente de θ y su derivada con respecto a θ también es 0.

Eliminando los términos de cero anteriores de la ecuación, nos queda (Ecuación 5):

Recordemos que de la Ecuación 2:

La Ecuación 5 evalúa el logaritmo de la primera parte de la Ecuación 2. Necesitamos relacionar la derivada de un término con su logaritmo. Hacemos esto utilizando la regla de la cadena y el truco del logaritmo de la derivada.

El truco del logaritmo de la derivada

Nos tomamos un desvío y utilizamos las reglas del cálculo para derivar un resultado, que utilizaremos para simplificar la ecuación anterior y hacerla adecuada para métodos computacionales.

En cálculo, la derivada de un logaritmo se puede expresar como:

Por lo tanto, al reorganizar la ecuación anterior, la derivada de x puede expresarse en términos de la derivada del logaritmo de x:

Esto a veces se llama el truco de la derivada logarítmica.

La regla de la cadena

Según la regla de la cadena, dado z(y) como una función de y, donde y en sí es una función de θ, y(θ), la derivada de z con respecto a θ se expresa como:

En este caso, y(θ) representa P(θ) y z(y) representa log(y). Así, 

Aplicando la regla de la cadena

Sabemos de cálculo que d(log(y)) / dy = 1/y. Usa esto en la primera expresión de la RHS arriba.

Mueve y al LHS y usa la notación:

y significa P(θ). Por lo tanto, la ecuación anterior es equivalente a:

Aplicando el truco del logaritmo derivado

El resultado anterior proporciona la primera expresión del LHS de la Ecuación 2 (mostrada abajo).

Usando el resultado en el LHS de la Ecuación 2, obtenemos:

Reorganizamos los términos bajo la integral del LHS como se muestra a continuación:

Derivando el resultado final

Observa que la expresión anterior contiene la expansión integral de una expectativa: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

Así, el RHS anterior puede expresarse como la expectativa:

Sustituimos la derivada de la probabilidad logarítmica en la expresión de la recompensa esperada:

En la ecuación anterior, sustituye el valor de ∇logP(θ) de la Ecuación 5 para obtener: 

Esta es la expresión para el gradiente de la función de recompensa según el teorema del gradiente de la política.

La intuición detrás del gradiente de la política

Los métodos de gradiente de la política convierten la salida de la política en una distribución de probabilidad. El agente muestrea esta distribución para elegir una acción. Los métodos de gradiente de la política ajustan los parámetros de la política. Esto lleva a actualizar esta distribución de probabilidad en cada iteración. La distribución de probabilidad actualizada tiene una mayor probabilidad de elegir acciones que conduzcan a recompensas más altas.

El algoritmo de gradiente de la política calcula el gradiente del retorno esperado con respecto a los parámetros de la política. Al mover los parámetros de la política en la dirección de este gradiente, el agente aumenta la probabilidad de elegir acciones que resulten en recompensas más altas durante el entrenamiento.

Esencialmente, las acciones que condujeron a mejores resultados se vuelven más propensas a ser elegidas en el futuro, mejorando gradualmente la política para maximizar las recompensas a largo plazo.

Implementación de Gradientes de Política en Python

Después de discutir los principios fundamentales de los gradientes de política, mostramos cómo implementarlos usando PyTorch y Gymnasium.

Configuración del entorno

Como primer paso, necesitamos instalar gymnasium y algunas bibliotecas de soporte como NumPy y PyTorch.

Para instalar gymnasium y sus dependencias en un servidor o máquina local, ejecuta:

$ pip install gymnasium 

Para instalarlo en un Cuaderno como Google Colab o DataLab, usa:

!pip install gymnasium

Importas estos paquetes dentro del entorno de Python:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

Codificación de un agente de gradiente de política simple

Cree una instancia del entorno utilizando el método .make().

env = gym.make('CartPole-v1')

Al igual que con otros métodos de aprendizaje automático, utilizamos una red neuronal para implementar el agente de gradiente de política.

CartPole-v1 es un entorno simple, por lo que diseñamos una red sencilla con 1 capa oculta con 64 neuronas. La dimensión de la capa de entrada es igual a las dimensiones del espacio de observación. La dimensión de la capa de salida es igual al tamaño del espacio de acciones del entorno. Por lo tanto, la red de política mapea estados observados a acciones. Dada una observación como entrada, la red predice la acción según la política.

El código a continuación implementa la red de política:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

Entrenando al agente

El entorno otorga una recompensa en cada paso de tiempo dependiendo del estado y la acción del agente. El enfoque de gradiente de política consiste en ejecutar descenso de gradiente en las recompensas acumuladas (retorno). El objetivo es maximizar el retorno total.

Para calcular el retorno en un episodio, se acumulan (con un factor de descuento) las recompensas de todos los pasos de tiempo en ese episodio. Además, normalizar los retornos es útil para garantizar un entrenamiento suave y estable. El código a continuación muestra cómo hacer esto:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

En cada iteración del pase hacia adelante, realizamos los siguientes pasos:

• Ejecutar el agente basado en la política actual utilizando la función .step(). La política predice la probabilidad de tomar la acción elegida en cada paso de tiempo.
• Recibir la recompensa del entorno basada en la acción del agente.
• Acumular recompensas paso a paso y las probabilidades logarítmicas de las acciones hasta que el agente alcance un estado terminal.

El código a continuación implementa el pase hacia adelante:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

Usando retropropagación y ascenso de gradiente para actualizar la política

En el aprendizaje automático tradicional:

• La pérdida se refiere a la diferencia entre la salida predicha y la salida real.
• Minimizamos la pérdida usando descenso de gradiente.

En RL:

• La pérdida es un proxy para la cantidad sobre la que se debe aplicar descenso (o ascenso) de gradiente.
• Maximizamos el retorno (recompensas acumulativas) utilizando ascenso de gradiente.
• El valor esperado del retorno se utiliza como un proxy para la pérdida en el descenso de gradiente. El valor esperado del retorno es el producto de:
• Los retornos esperados de cada paso con
• La probabilidad de elegir la acción muestreada en cada paso.
• Para aplicar el ascenso de gradiente utilizando retropropagación, utilizamos el negativo de la pérdida.

El código a continuación calcula la pérdida:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

Similar a los algoritmos de aprendizaje automático estándar, para actualizar la política, se ejecuta la retropropagación con respecto a la función de pérdida. El método update_policy() a continuación invoca el método calculate_loss(). Luego ejecuta la retropropagación sobre esta pérdida para actualizar los parámetros de la política, es decir, los pesos del modelo de la red de políticas.

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

El bucle de entrenamiento

Utilizamos las funciones definidas anteriormente para entrenar la política. Antes de comenzar el entrenamiento, necesitamos:

• Una política no entrenada inicializada como una instancia aleatorizada de la clase PolicyNetwork.
• Un optimizador que utilice el algoritmo Adam.
• Hiperparámetros para el factor de descuento, tasa de aprendizaje, tasa de abandono, umbral de recompensa y el número máximo de épocas de entrenamiento.

Iteramos a través del bucle de entrenamiento hasta que el retorno promedio supere el umbral de recompensa. En cada iteración, ejecutamos los siguientes pasos:

• Para cada episodio, ejecutar el pase hacia adelante una vez. Recolectar la probabilidad de registro de acciones, los retornos paso a paso y el retorno total de ese episodio. Acumular los retornos episódicos en un arreglo.
• Calcular la pérdida utilizando las probabilidades de registro y los retornos paso a paso. Ejecutar la retropropagación sobre la pérdida. Utilizar el optimizador para actualizar los parámetros de la política.
• Verificar si el retorno promedio sobre N_TRIALS supera el umbral de recompensa.

El código a continuación implementa estos pasos:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

Ejecuta el programa de entrenamiento llamando a la función main().

main()

Este cuaderno de DataLab contiene la implementación anterior del algoritmo de gradiente de políticas. Puedes ejecutarlo directamente o usarlo como punto de partida para modificar el algoritmo.

Ventajas y desafíos de los métodos de gradiente de políticas

Los métodos de gradiente de políticas ofrecen varias ventajas, como:

• Manejo de espacios de acción continuos: Los métodos basados en valores (como el Q-learning) son ineficientes con espacios de acción continuos porque necesitan estimar valores en todo el espacio de acción. Los métodos de gradiente de política pueden optimizar directamente la política utilizando el gradiente de los retornos esperados. Este enfoque funciona bien con distribuciones de acción continua. Por lo tanto, los métodos de gradiente de política son adecuados para tareas como el control robótico que se basan en espacios de acción continuos.
• Políticas estocásticas: Los métodos de gradiente de política pueden aprender políticas estocásticas, que dan una probabilidad de seleccionar cada posible acción. Esto permite al agente probar una variedad de acciones y reduce el riesgo de quedarse atascado en óptimos locales. Ayuda en entornos complejos donde el agente necesita explorar el espacio de acción para encontrar la política óptima. La naturaleza estocástica ayuda a equilibrar la exploración (probar nuevas acciones) y la explotación (elegir las acciones mejor conocidas), lo cual es crucial para entornos con incertidumbre o recompensas escasas.
• Optimización directa de políticas: Los gradientes de políticas optimizan la política directamente en lugar de usar funciones de valor. En espacios de acción continuos o de alta dimensionalidad, aproximar valores para cada acción puede volverse computacionalmente costoso. Por lo tanto, los métodos basados en políticas funcionan bien en tales entornos. 

A pesar de sus muchas ventajas, los métodos de gradientes de políticas tienen algunos desafíos inherentes:

• Alta varianza en las estimaciones de gradiente: Los métodos de gradiente de políticas seleccionan acciones muestreando una distribución de probabilidad. En efecto, muestrean la trayectoria para estimar el retorno esperado. Debido a que el proceso de muestreo es inherentemente aleatorio, los retornos estimados en iteraciones posteriores pueden tener una alta varianza. Esto puede hacer que sea difícil para el agente aprender eficientemente porque las actualizaciones de la política pueden fluctuar significativamente entre iteraciones.
• Inestabilidad durante el entrenamiento:
• Los métodos de gradiente de políticas son sensibles a hiperparámetros como el. Si la tasa de aprendizaje es demasiado alta, las actualizaciones a los parámetros de la política pueden ser demasiado grandes, causando que el entrenamiento no alcance los parámetros óptimos. Por otro lado, si la tasa de aprendizaje es demasiado pequeña, la convergencia puede ser lenta.
• Los métodos de gradiente de política necesitan equilibrar la exploración y la explotación. Si el agente no explora lo suficiente, puede que no alcance el vecindario de la política óptima. Por otro lado, si explora demasiado, no convergerá en la política óptima y oscilará alrededor del espacio de acción.
• Ineficiencia de la muestra: Los métodos de gradiente de política estiman el retorno siguiendo cada política hasta la terminación y acumulando las recompensas de cada paso. Por lo tanto, necesitan muchas interacciones con el entorno para obtener un gran número de trayectorias de muestra. Esto es ineficiente y costoso para entornos con grandes espacios de estado o acción.

Soluciones para la estabilidad

Dado que la inestabilidad es un problema relativamente común en los métodos de gradiente de política, los desarrolladores han adoptado varias soluciones para estabilizar el proceso de entrenamiento. A continuación, presentamos soluciones comunes para estabilizar el entrenamiento utilizando gradientes de política: 

Uso de funciones de línea base

Debido a un muestreo ineficiente, los gradientes de los rendimientos estimados durante las iteraciones de entrenamiento pueden tener una alta varianza, lo que hace que el entrenamiento sea inestable y lento. Un enfoque común para reducir la varianza es utilizar funciones de línea base, como el método Advantage Actor-Critic (A2C). La idea es utilizar un proxy (la función de ventaja) en lugar del rendimiento estimado para la función objetivo. 

La ventaja se calcula como la diferencia entre el rendimiento real de la trayectoria muestreada y el rendimiento esperado dada el estado inicial. Este enfoque implica utilizar la función de valor como el valor esperado de los estados y pares de estados-acción. Al representar la pérdida como la diferencia entre el rendimiento real y el rendimiento esperado en lugar de solo los rendimientos, A2C reduce la varianza en la función de pérdida y, por lo tanto, en los gradientes, lo que hace que el entrenamiento sea más estable. 

Utilizando la regularización de entropía

En ciertos entornos, como aquellos con recompensas dispersas (solo muy pocos estados dan una recompensa), la política adopta rápidamente un enfoque determinista. También adopta un enfoque codicioso y explota los caminos que ya ha explorado. Esto evita una mayor exploración y a menudo conduce a la convergencia a óptimos locales y políticas subóptimas.

La solución es fomentar la exploración sobre penalizar la política cuando se vuelve demasiado determinista. Esto se logra agregando un término basado en entropía a la función objetivo. La entropía mide la cantidad de aleatoriedad en la política. Cuanta mayor sea la entropía, más aleatoriedad en las acciones elegidas por el agente. Este término basado en entropía es el producto del coeficiente de entropía y la entropía de la política actual.

Hacer que la entropía sea parte de la función objetivo ayuda a lograr un equilibrio entre la explotación y la exploración.

Extensiones del Gradiente de Política

Entre las diversas extensiones de los métodos de gradiente de política, una de las más fundamentales es el algoritmo REINFORCE. Proporciona una implementación sencilla del teorema del gradiente de política y es la base para técnicas más avanzadas.

Algoritmo REINFORCE

El algoritmo REINFORCE, también conocido como Monte Carlo Reinforce, es una de las implementaciones básicas del teorema del gradiente de política. Utiliza métodos de Monte Carlo para estimar retornos y gradientes de política. Al seguir el algoritmo REINFORCE, el agente toma muestras directamente de todas las acciones (desde el estado inicial hasta el estado terminal) del entorno. Esto contrasta con otros métodos como TD-Learning y Programación Dinámica, que basan sus acciones en estimaciones de la función de valor.

A continuación, presentamos los pasos básicos del algoritmo REINFORCE:

• Inicializa la política con parámetros aleatorios
• Repite múltiples episodios de entrenamiento. Para cada episodio:
• Genera cada paso del episodio completo de la siguiente manera:
• Pasa el estado a la función de política.
• La función de política genera probabilidades para cada acción posible.
• Muestrea aleatoriamente una acción de esta distribución de probabilidad.
• Para cada estado en el episodio, estima los retornos (recompensas acumuladas descontadas) hasta el paso.
• Estima el gradiente de la función objetivo (según el teorema del gradiente de política), expresado como el producto de los retornos por pasos y las probabilidades de acción para cada paso.
• Actualiza los parámetros de la política aplicando los gradientes.

Para cada política, puedes muestrear una única trayectoria para estimar el gradiente (como se muestra arriba) o promediar el gradiente en múltiples trayectorias muestreadas bajo la misma política.

Métodos de actor-crítico

Los métodos de actor-crítico combinan métodos de gradiente de política (como REINFORCE) con funciones de valor.

• El funcionamiento del actor es similar a los métodos de gradiente de política. El actor implementa la política, seleccionando acciones en cada paso basado en la política. Actualiza la política siguiendo el gradiente del retorno esperado.
• El crítico implementa la función de valor, que se utiliza como una línea base (discutida en la sección anterior). Esto ayuda a que el entrenamiento sea más eficiente y estable.

Los métodos de gradiente de política como REINFORCE estiman los gradientes a lo largo de cada trayectoria usando el retorno crudo. Debido a que un proceso de muestreo dibuja estas trayectorias, puede llevar a grandes variaciones en los retornos y gradientes. Utilizar una función de ventaja en lugar de los retornos crudos resuelve este problema. La función de ventaja es la diferencia entre los retornos reales y esperados (es decir, la función de valor). Los métodos de actor-crítico son una clase de algoritmos. Cuando el crítico se implementa utilizando la función de ventaja (el enfoque más común), también se le llama Actor-Crítico de Ventaja (A2C).

Optimización de Política Proximal (PPO)

En entornos complejos, los métodos de actor-crítico como A2C por sí solos no son suficientes para controlar la varianza en los retornos y gradientes. En tales casos, restringir artificialmente la cantidad por la cual la política puede cambiar en cada iteración ayuda. Esto obliga a que la política actualizada (después del ascenso de gradiente) se encuentre en el vecindario de la política antigua.

Métodos como Optimización de Política Proximal realizan dos modificaciones a los gradientes de política:

• Utilizar una función de ventaja. Normalmente, esta función de ventaja utiliza la función de valor como referencia. En esto, son similares a los métodos A2C.
• Restringir la cantidad por la cual los parámetros de la política pueden cambiar en cada iteración. Esto se hace utilizando una función objetivo de sustituto recortada. El algoritmo especifica un rango dentro del cual debe situarse la proporción de la nueva política con respecto a la antigua política. Cuando la proporción (después de la actualización del gradiente) excede estos valores predeterminados, se recorta para situarse dentro del rango.

Así, PPO mejora significativamente los métodos de gradiente de política convencionales, lo que aumenta la estabilidad en entornos complejos. La función objetivo recortada evita grandes varianzas en los rendimientos y gradientes que puedan desestabilizar las actualizaciones de la política. Para lograr un equilibrio entre exploración y explotación, también es posible modificar PPO para usar regularización de entropía. Esto se hace añadiendo un término de entropía (un parámetro de escala multiplicado por la entropía de la política) a la función objetivo.

Avances recientes

Los gradientes de política están entre los métodos más antiguos utilizados para resolver problemas de RL. Tras la llegada de GPUs rápidas, se han propuesto diversos enfoques nuevos para aplicar técnicas modernas de ML a los gradientes de política.

Aprendizaje reforzado impulsado por gradientes.

En los últimos años, se ha avanzado en la aplicación de métodos como gradient boosting a algoritmos de RL. El gradient boosting combina las predicciones de múltiples modelos débiles para generar un único modelo fuerte. Esto se conoce como Refuerzo con Aumento de Gradiente (GBRL). GBRL es un paquete de Python similar a XGBoost que implementa estas técnicas para algoritmos de RL.

Transfer Reinforcement Learning

Transfer learning (TL) es una técnica en la que el conocimiento adquirido por un modelo se aplica para mejorar el rendimiento de otro modelo. Transfer learning es útil porque entrenar modelos de ML desde cero es costoso. Los enfoques de TL se han utilizado con gradientes de políticas para mejorar el rendimiento de los modelos de RL. Este enfoque se llama Transfer Reinforcement Learning (TRL).

Conclusión

Los gradientes de política están entre los enfoques más fundamentales para resolver problemas de RL.

En este artículo, presentamos los primeros principios de los gradientes de política y mostramos cómo derivar el teorema del gradiente de política. También demostramos cómo implementar un algoritmo simple basado en gradientes usando PyTorch en un entorno de Gimnasio. Por último, discutimos los desafíos prácticos y las extensiones comunes al algoritmo básico de gradiente de política.

Si deseas profundizar tu comprensión del aprendizaje por refuerzo y del aprendizaje profundo con PyTorch, echa un vistazo a estos cursos:

• Track de Aprendizaje por Refuerzo – Aprende los fundamentos de RL, desde métodos basados en valor hasta técnicas de optimización de políticas.
• Introducción al Aprendizaje Profundo con PyTorch – Obtén experiencia práctica con PyTorch y construye modelos de aprendizaje profundo desde cero.