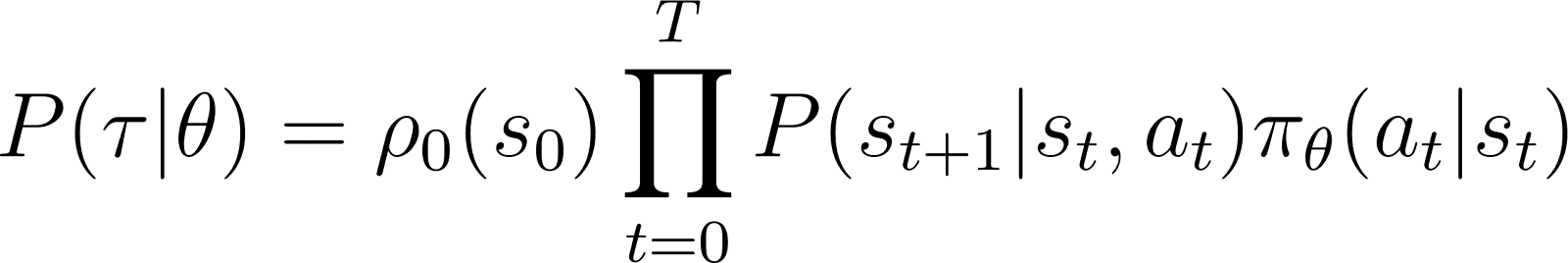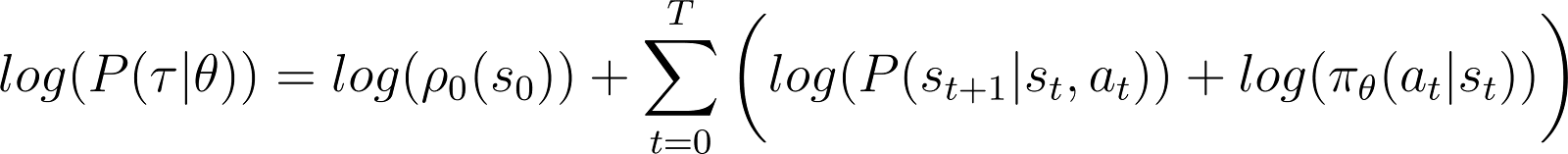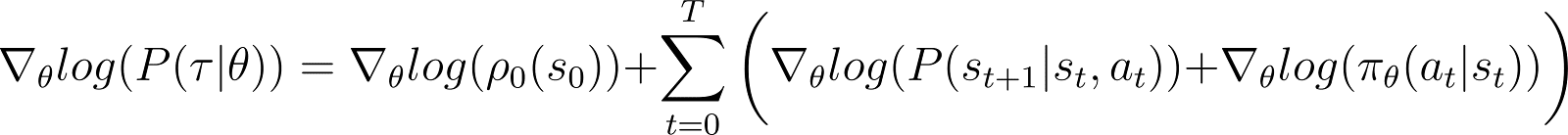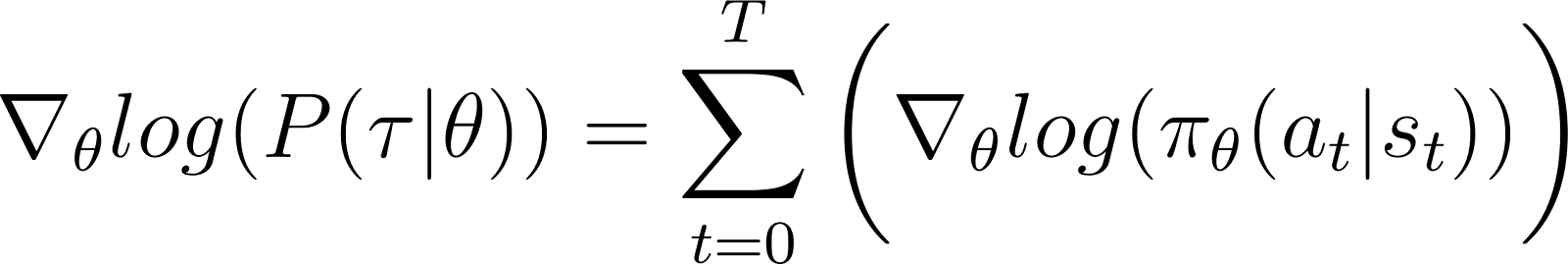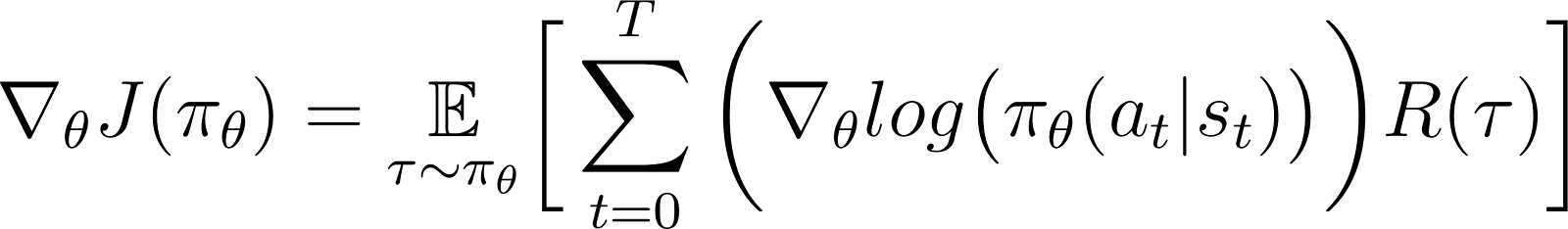정책 그래디언트 정리 설명: 실습 소개

정책 그레디언트 방법을 사용하는 이유?

정책 그레디언트 방법의 중요한 장점 중 하나는 전통적인 가치 기반 접근법이 어려워하는 복잡한 행동 공간을 다룰 수 있는 능력입니다.

고차원 행동 공간 다루기

가치 기반 방법인 Q-러닝(Q-learning)은 모든 가능한 행동에 대한 가치 함수를 추정함으로써 작동합니다. 환경의 행동 공간이 연속적이거나 이산적이지만 큰 경우에는 이 작업이 어려워집니다.

정책 그래디언트 방법은 정책을 매개변수화하고 누적 보상에 대한 그래디언트를 정책 매개변수에 대해 추정합니다. 이 그래디언트를 사용하여 정책을 직접 최적화하여 매개변수를 업데이트합니다. 따라서 고차원 또는 연속적인 행동 공간을 효율적으로 처리할 수 있습니다. 정책 그래디언트는 또한 인간 피드백을 활용한 강화 학습(RLHF) 방법의 기초입니다.

정책을 매개변수화하고 해당 매개변수를 그래디언트에 기반하여 조정함으로써 정책 그래디언트는 연속적이고 고차원인 행동을 효율적으로 처리할 수 있습니다. 이 직접적인 접근은 더 나은 일반화와 더 유연한 탐사를 가능하게 하며, 로봇 제어 및 기타 복잡한 환경과 같은 작업에 적합합니다.

확률적 정책 학습

주어진 관찰 세트:

• 결정론적 정책은 에이전트가 취하는 행동을 지정합니다.
• 확률적 정책은 에이전트가 각 행동을 선택할 확률과 함께 행동 집합을 제공합니다.

확률적 정책을 따를 때, 동일한 관찰이 서로 다른 반복에서 다른 행동 선택으로 이어질 수 있습니다. 이는 행동 공간을 탐색하고 정책이 국소 최적해에 갇히는 것을 방지합니다. 따라서 확률적 정책은 최대 수익을 찾는 경로를 발견하는 데 필수적인 환경에서 유용합니다.

정책 기반 방법에서 정책 출력은 각 가능한 행동에 확률이 할당된 확률 분포로 변환됩니다. 에이전트는 이 분포를 샘플링하여 행동을 선택하므로 확률적 정책을 구현할 수 있습니다. 따라서 정책 그래디언트 방법은 탐색을 개발과 결합하여 복잡한 보상 구조를 갖는 환경에 유용합니다.

정책 그래디언트 정리 유도

유도에 들어가기 전에, 증명 전반에 걸쳐 사용되는 수학적 표기법과 주요 개념을 확립하는 것이 중요합니다.

수학적 표기법 및 전제 조건

앞서 언급된 바와 같이, 정책 그래디언트 정리는 기대 수익의 도함수가 수익과 정책의 로그 도함수의 곱의 기대값이라는 것을 나타냅니다.

정책 그래디언트 정리를 유도하기 전에, 다음과 같은 표기법을 소개합니다:

• E[X]는 확률 변수 X의 확률적 기대값을 나타냅니다.
• 수학적으로 정책은 다른 관측에 따라 다른 행동을 선택할 확률을 제공하는 확률 행렬로 표현됩니다. 정책은 일반적으로 매개변수화된 함수로 모델링되는데, 매개변수는 θ로 표현됩니다.
• π_θ 는 θ에 의해 매개변수화된 정책을 가리킵니다. 실제로 이러한 매개변수는 정책을 모델링하는 신경망의 가중치입니다.
• 궤적, τ, 일반적으로 무작위 초기 상태부터 현재 타임스텝 또는 종단 상태까지의 상태 시퀀스를 가리킵니다.
• ∇_θf 함수의 그래디언트를 나타냅니다. f 매개변수 θ에 대한 함수
• J(J(πθ)) 에이전트가 따르는 정책 πθ에 따라 달성하는 예상 수익을 나타냅니다. 이는 기울기 상승을 위한 목적 함수이기도 합니다.
• 환경은 에이전트의 행동에 따라 각 타임스텝마다 보상을 제공합니다. 반환은 초기 상태부터 현재 타임스텝까지의 누적 보상을 가리킵니다.
• R(τ)은 τ 궤적 상에서 발생한 수익을 나타냅니다. 

도출 단계

우리는 목적 함수의 확장을 통해 정책 경사 정리를 유도하고 증명하는 방법을 보여줍니다. 로그 미분 트릭을 사용하여 처음 원칙부터 시작합니다.

목적 함수(Equation 1)

정책 경사 방법에서의 목적 함수는 반환값입니다.

J 정책 π 에 따라 궤적을 따라 축적된 매개변수로 표현된 목적 함수는 다음과 같습니다:

위의 방정식에서:

• 좌변(LHS)은 정책π_θ을 따를 때 얻는 기대수익입니다.
• 오른쪽 측면 (RHS)은 각 단계에서 생성된 정책 π_θ을 따라 생성된 궤적 τ의 기대값입니다. R(τ) 을 통해 생성된 반환값τ에 대한 궤적 의 기대값입니다.

목적 함수의 미분(식 2)

위의 식의 양쪽을 θ에 대해 미분하면:

기대값의 그래디언트(식 3)

기대값(우변)은 다음의 곱에 대한 적분으로 표현될 수 있습니다:

• 경로 τ를 따를 확률
• 트라젝토리에서 생성된 반환

따라서, 방정식 2의 RHS는 다음과 같이 다시 기술됩니다:

적분의 기울기는 기울기의 적분과 같습니다. 따라서 위 식에서 우리는 기울기 ∇_θ을 적분 기호 아래로 가져올 수 있습니다. 따라서 RHS는 다음과 같습니다:

따라서, 방정식 2는 다음과 같이 다시 쓸 수 있습니다:

경로의 확률 (방정식 4)

우리는 이제 P(τ|θ), 에이전트가 정책 매개변수 θ 주어진 정책 π_θ (그리고 정책)을 따르는 확률을 살펴보겠습니다. 이동경로는 일련의 단계로 구성됩니다. 따라서:

• 경로를 얻을 확률은 다음의 곱입니다:
• 모든 개별 단계를 따르는 확률.

• 시간 단계 t에, 에이전트는 상태 s에서 상태 s_t+1로 이동합니다. a_t의 행동을 따르며 발생할 확률은 다음의 곱으로 주어집니다:
• 정책이 행동 a_t를 상태 s_t에서 예측할 확률
• 상태 s_t+1에 도달할 확률은 a_t 및 상태 s_t

따라서 초기 상태 s₀에서, 에이전트가 정책 π_θτ를 기반으로 경로를 따를 확률은 다음과 같습니다:

간단하게 만들기 위해, 우리는 위의 RHS에서 제품을 합으로 표현하고자 합니다. 그래서 위의 방정식 양쪽에 로그를 취합니다:

로그 확률의 도함수 (방정식 5)

이제 우리는 위의 방정식에서 로그 확률에 대해 θ의 도함수를 취합니다.

위의 방정식의 RHS에서:

• 첫 번째 항 로그 ρ₀(s₀)은 θ에 대해 상수입니다. 따라서 그 도함수는 0입니다.
• 합계 안의 첫 번째 용어P(s_t+1|s_t, a_t)도 θ 및 θ에 대한 도함수도 0입니다. 

위의 제로항을 방정식에서 제거하면 (방정식 5)이 남습니다:

방정식 2에서 다음을 상기하십시오:

방정식 5는 방정식 2의 RHS의 첫 번째 부분의 로그를 계산합니다. 우리는 항의 미분과 그 로그를 관련시켜야 합니다. 이를 체인 룰과 로그-미분 트릭을 사용하여 수행합니다.

로그-미분 트릭

우리는 우회로를 취하고 미적분학의 규칙을 사용하여 결과를 유도하고, 이를 사용하여 이전 방정식을 단순화하고 계산 방법에 적합하도록 만듭니다.

미적분학에서 로그의 미분은 다음과 같이 표현될 수 있습니다:

이와 같이 방정식을 재배열하여, x의 도함수를 x의 로그의 도함수로 표현할 수 있습니다:

이를 로그 도함수 트릭이라고도 합니다.

연쇄 법칙

체인 룰에 따르면, z(y)는 함수로y에 대해 주어지며, y은 그 자체가 θ의 함수이다. y(θ)의 도함수는 다음과 같이 주어진다:

이 경우에는 y(θ)은 P(θ)을 나타내며 z(y)은 log(y)를 나타냅니다. 따라서,

연쇄 법칙 적용

미적분학에서 우리는 d(log(y)) / dy = 1/y라는 것을 알고 있습니다. 이를 위의 RHS 첫 번째 식에 사용하세요.

y를 LHS로 이동시키고 표기법을 사용하세요:

y는 P(θ)를 나타냅니다. 따라서 위의 방정식은 다음과 같습니다:

로그-미분 트릭 적용

위의 결과는 아래에 표시된 방정식 2의 우변의 첫 번째 표현을 제공합니다.

방정식 2의 우변에서 결과를 사용하면 다음과 같습니다:

우변의 적분 아래의 항들을 다음과 같이 재배치합니다:

최종 결과 도출하기

위의 표현이 기대값의 적분 확장을 포함하고 있음을 관찰하십시오: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

따라서 위의 RHS는 기대값으로 표현될 수 있습니다:

우리는 기대 보상의 표현에서 로그 확률의 도함수를 대체합니다:

위의 방정식에서 ∇logP(θ)를 방정식 5에서 대입하여 얻습니다: 

정책 경량 정리에 따른 보상 함수의 기울기 표현입니다.

정책 경량의 직관

정책 경량 방법은 정책의 출력을 확률 분포로 변환합니다. 에이전트는 이 분포에서 샘플링하여 행동을 선택합니다. 정책 경량 방법은 정책 매개변수를 조정합니다. 이로 인해 각 반복에서 이 확률 분포가 업데이트됩니다. 업데이트된 확률 분포는 더 높은 보상으로 이어지는 행동을 선택할 가능성이 높아집니다. 

정책 경량 알고리즘은 정책 매개변수에 대한 기대 수익의 기울기를 계산합니다. 이 기울기의 방향으로 정책 매개변수를 이동시킴으로써 에이전트는 훈련 동안 더 높은 보상으로 이어지는 행동을 선택할 확률을 증가시킵니다.

본질적으로, 더 나은 결과로 이어진 행동은 미래에 선택될 가능성이 높아지며, 점진적으로 정책을 개선하여 장기 보상을 극대화합니다.

파이썬에서 정책 경량 구현하기

정책 그라디언트의 기본 원리에 대해 논의한 후, PyTorch와 Gymnasium을 사용하여 이를 구현하는 방법을 보여줍니다.

환경 설정

첫 번째 단계로 gymnasium과 NumPy 및 PyTorch와 같은 몇 가지 지원 라이브러리를 설치해야 합니다.

서버 또는 로컬 머신에 gymnasium 및 해당 종속성을 설치하려면 다음을 실행하십시오:

$ pip install gymnasium 

Google Colab 또는 DataLab과 같은 노트북을 사용하여 설치하려면 다음을 사용하십시오:

!pip install gymnasium

이러한 패키지들을 Python 환경 내에서 가져옵니다:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

간단한 정책 그라디언트 에이전트 코딩

.make() 메서드를 사용하여 환경의 인스턴스를 생성합니다.

env = gym.make('CartPole-v1')

다른 기계 학습 방법들과 마찬가지로, 정책 그래디언트 에이전트를 구현하기 위해 신경망을 사용합니다.

CartPole-v1은 간단한 환경이므로, 64개의 뉴런을 가진 1개의 은닉층으로 구성된 간단한 네트워크를 설계합니다. 입력층의 차원은 관찰 공간의 차원과 동일합니다. 출력층의 차원은 환경의 행동 공간의 크기와 동일합니다. 따라서 정책 네트워크는 관찰된 상태를 행동으로 매핑합니다. 관찰을 입력으로 주면, 네트워크는 정책에 따라 예측된 행동을 출력합니다.

아래 코드는 정책 네트워크를 구현합니다:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

에이전트 훈련

환경은 에이전트의 상태와 행동에 따라 각 타임스텝에서 보상을 제공합니다. 정책 그래디언트 접근법은 누적 보상(수익)에 대해 경량 하강법을 실행하는 것으로 구성됩니다. 목표는 총 수익을 최대화하는 것입니다.

에피소드에서 수익을 계산하려면, 해당 에피소드의 모든 타임스텝에서 보상을 누적(할인 요인과 함께)합니다. 또한, 수익을 정규화하는 것은 원활하고 안정적인 훈련을 보장하는 데 유용합니다. 아래 코드는 이를 수행하는 방법을 보여줍니다:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

각 반복에서 순방향 패스를 수행할 때, 우리는 다음 단계를 수행합니다:

• 현재 정책을 기반으로 에이전트를 실행합니다 .step() 함수와 함께. 정책은 각 시간 단계에서 선택한 행동을 취할 확률을 예측합니다.
• 에이전트의 행동에 따라 환경으로부터 보상을 받습니다.
• 에이전트가 터미널 상태에 도달할 때까지 단계별 보상과 행동의 로그 확률을 누적합니다.

아래 코드는 순방향 패스를 구현합니다:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

정책을 업데이트하기 위해 역전파와 경량 상승 사용

전통적인 기계 학습:

• 손실은 예측된 출력과 실제 출력 간의 차이를 의미합니다.
• 우리는 경량 하강법을 사용하여 손실을 최소화합니다.

RL에서는:

• 손실은 경사 하강(또는 상승)이 적용될 양을 대리합니다.
• 우리는 경사 상승을 사용하여 수익(누적 보상)을 최대화합니다.
• 예상 수익 값은 경사 하강을 위한 손실을 대리로 사용합니다. 예상 수익 값은 다음의 곱으로 이루어집니다:
• 각 단계에서 예상되는 수익과
• 각 단계에서 샘플링된 작업을 선택할 확률.
• 역전파를 사용하여 경사 상승을 적용하기 위해, 우리는 손실의 음수를 사용합니다.

아래 코드는 손실을 계산합니다:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

표준 머신 러닝 알고리즘과 유사하게, 정책을 업데이트하기 위해 손실 함수에 대해 역전파를 실행합니다. update_policy() 메서드는 calculate_loss() 메서드를 호출합니다. 그런 다음 이 손실에 대해 역전파를 실행하여 정책 매개변수, 즉 정책 네트워크의 모델 가중치를 업데이트합니다.

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

훈련 루프

우리는 앞서 정의한 기능을 사용하여 정책을 훈련합니다. 훈련을 시작하기 전에 필요한 것들은:

• 정책 네트워크 클래스의 무작위 인스턴스로 초기화된 훈련되지 않은 정책.
• Adam 알고리즘을 사용하는 옵티마이저.
• 할인율, 학습률, 드롭아웃 비율, 보상 임계값 및 최대 훈련 에폭 수에 대한 하이퍼파라미터.

우리는 평균 수익이 보상 임계값을 초과할 때까지 훈련 루프를 반복합니다. 각 반복에서 다음 단계를 실행합니다:

• 각 에피소드에 대해 한 번 전방 패스를 실행합니다. 행동의 로그 확률, 단계별 수익 및 해당 에피소드의 총 수익을 수집합니다. 에피소드 수익을 배열에 축적합니다.
• 로그 확률과 단계별 수익을 사용하여 손실을 계산합니다. 손실에 대해 역전파를 실행합니다. 옵티마이저를 사용하여 정책 매개변수를 업데이트합니다.
• N_TRIALS의 평균 수익이 보상 임계값을 초과하는지 확인합니다.

아래 코드는 이러한 단계를 구현합니다:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

main() 함수를 호출하여 훈련 프로그램을 실행하세요:

main()

이 DataLab 워크북은 정책 기울기 알고리즘의 위 구현을 포함하고 있습니다. 이를 직접 실행하거나 알고리즘 수정의 출발점으로 사용할 수 있습니다.

정책 기울기 방법의 장점과 도전 과제

정책 기울기 방법은 다음과 같은 여러 가지 장점을 제공합니다:

• 연속적인 액션 공간 다루기: 값 기반 방법(예: Q-러닝)은 전체 액션 공간에 대한 값을 추정해야 하기 때문에 연속적인 액션 공간에서 효율적이지 않습니다. 정책 그라디언트 방법은 기대 수익의 그라디언트를 사용하여 정책을 직접 최적화할 수 있습니다. 이 접근 방식은 연속적인 액션 분포에서 잘 작동합니다. 따라서 정책 그라디언트 방법은 연속적인 액션 공간에 기반을 둔 로봇 제어와 같은 작업에 적합합니다.
• 확률적 정책: 정책 그라디언트 방법은 확률적 정책을 학습할 수 있습니다 – 각 가능한 액션을 선택할 확률을 제공합니다. 이를 통해 에이전트는 다양한 액션을 시도할 수 있고 지역 최적해에 갇히는 위험을 줄일 수 있습니다. 이는 에이전트가 최적 정책을 찾기 위해 액션 공간을 탐색해야 하는 복잡한 환경에서 도움이 됩니다. 확률적 성격은 탐험(새로운 액션 시도)과 개척(가장 잘 알려진 액션 선택)을 균형있게 유지해주어 불확실성이나 희소 보상이 있는 환경에서 중요합니다.
• 정책 최적화: 정책 그래디언트는 가치 함수를 사용하는 대신 정책을 직접 최적화합니다. 연속 또는 고차원 행동 공간에서는 모든 행동에 대한 가치를 근사하는 것이 계산적으로 비용이 많이 듭니다. 따라서 정책 기반 방법은 이러한 환경에서 잘 작동합니다. 

그들의 많은 장점에도 불구하고, 정책 그래디언트 방법에는 몇 가지 본질적인 도전 과제가 있습니다:

• 그래디언트 추정의 높은 분산: 정책 그래디언트 방법은 확률 분포를 샘플링하여 행동을 선택합니다. 이는 기대 수익을 추정하기 위해 경로를 샘플링하는 효과를 가집니다. 샘플링 과정이 본질적으로 무작위적이기 때문에 후속 반복에서 추정된 수익은 높은 분산을 가질 수 있습니다. 이로 인해 에이전트가 효율적으로 학습하기 어려울 수 있으며, 정책 업데이트가 반복 간에 크게 변동할 수 있습니다.
• 훈련 중 불안정성:
• 정책 그래디언트 방법은 하이퍼파라미터에 민감합니다. 학습률이 너무 높으면 정책 매개변수에 대한 업데이트가 너무 커져 최적의 매개변수를 놓칠 수 있습니다. 반대로, 학습률이 너무 낮으면 수렴 속도가 느릴 수 있습니다.
• 정책 그래디언트 방법은 탐험과 활용을 균형 있게 유지해야 합니다. 에이전트가 충분히 탐험하지 않으면 최적 정책의 근처에 도달하지 못할 수 있습니다. 반대로, 너무 많이 탐험하면 최적 정책에 수렴하지 못하고 행동 공간 주변을 오실레이션할 수 있습니다.
• 샘플 비효율성: 정책 그래디언트 방법은 각 정책을 종료까지 따라가며 각 단계에서의 보상을 누적하여 반환을 추정합니다. 따라서, 환경과 많은 상호작용이 필요하여 많은 샘플 경로를 얻어야 합니다. 이는 상태나 행동 공간이 큰 환경에서 비효율적이고 비용이 많이 들 수 있습니다.

안정성을 위한 솔루션

정책 그래디언트 방법에서 불안정성이 비교적 흔한 문제이기 때문에, 개발자들은 훈련 과정을 안정화하기 위해 다양한 솔루션을 채택해 왔습니다. 아래에서 정책 그래디언트를 사용한 훈련을 안정화하는 일반적인 솔루션을 소개합니다: 

베이스라인 함수 사용

비효율적인 샘플링으로 인해 교육 반복 중에 추정된 수익의 기울기는 높은 분산을 가질 수 있어 교육이 불안정하고 느려질 수 있습니다. 분산을 줄이는 일반적인 접근 방식은 Advantage Actor-Critic (A2C) 방법과 같은 베이스라인 함수를 사용하는 것입니다. 이 아이디어는 목적 함수를 위해 추정된 수익 대신 대리자(이득 함수)를 사용하는 것입니다.

이득은 샘플된 경로에서의 실제 수익과 초기 상태가 주어졌을 때 예상되는 수익 간의 차이로 계산됩니다. 이 접근 방식은 상태와 상태-행동 쌍의 예상 값으로 값 함수를 사용함을 포함합니다. 반환만으로가 아닌 실제 수익과 예상 수익 간의 차이로 손실을 표현함으로써, A2C는 손실 함수와 그래디언트의 분산을 줄이고 교육을 더 안정적으로 만듭니다.

엔트로피 정규화를 사용하는

일부 환경에서는 희소 보상(매우 적은 상태만 보상을 제공)이 있는 환경에서는 정책이 빠르게 결정론적 접근을 채택합니다. 또한 탐욕적인 접근을 채택하고 이미 탐색한 경로를 이용합니다. 이는 추가적인 탐험을 방해하고 종종 국소 최적점 및 최적 정책으로 수렴하도록 합니다.

해결책은 정책이 너무 결정론적일 때 처벌하는 탐색을 장려하는 것입니다. 이는 목적 함수에 엔트로피 기반 항을 추가함으로써 이루어집니다. 엔트로피는 정책의 무작위성을 측정합니다. 엔트로피가 클수록 에이전트가 선택하는 행동의 무작위성이 커집니다. 이 엔트로피 기반 항은 엔트로피 계수와 현재 정책의 엔트로피의 곱입니다.

엔트로피를 목적 함수의 일부로 만드는 것은 착취와 탐색 간의 균형을 이루는 데 도움이 됩니다.

정책 그래디언트 확장

정책 그래디언트 방법의 다양한 확장 중에서 가장 기본적인 것 중 하나는 REINFORCE 알고리즘입니다. 이 알고리즘은 정책 그래디언트 정리를 간단하게 구현하며, 더 발전된 기술의 기초가 됩니다.

REINFORCE 알고리즘

REINFORCE 알고리즘은 몬테카를로 REINFORCE로도 알려져 있으며 정책 그래디언트 이론의 기본 구현 중 하나입니다. 이는 몬테카를로 방법을 사용하여 반환값과 정책 그래디언트를 추정합니다. REINFORCE 알고리즘을 따를 때 에이전트는 환경으로부터 모든 행동 (초기 상태부터 종단 상태까지)을 직접 샘플링합니다. 이는 TD-Learning 및 동적 프로그래밍과 같은 다른 방법과 대조됩니다. 이러한 방법들은 가치 함수 추정에 기반하여 행동을 부트스트랩합니다.

아래에서 REINFORCE 알고리즘의 기본 단계를 제시합니다:

• 정책을 무작위 매개변수로 초기화합니다.
• 여러 번의 훈련 에피소드를 반복합니다. 각 에피소드마다:
• 전체 에피소드의 각 단계를 다음과 같이 생성합니다:
• 상태를 정책 함수에 전달합니다.
• 정책 함수는 각 가능한 행동에 대한 확률을 생성합니다.
• 이 확률 분포에서 행동을 무작위로 샘플링합니다.
• 에피소드의 각 상태에 대해, 스텝까지의 수익(할인 누적 보상)을 추정합니다.
• 목표 함수의 기울기를 추정합니다(정책 기울기 정리에 따라), 이는 스텝별 수익과 각 스텝의 행동 확률의 곱으로 표현됩니다.
• 기울기를 적용하여 정책 매개변수를 업데이트합니다.

각 정책에 대해 단일 궤적을 샘플링하여 그래디언트를 추정하거나(위와 같이) 동일한 정책 하에 샘플링된 여러 궤적의 그래디언트를 평균낼 수 있습니다.

액터-비평가 방법

액터-비평가 방법은 정책 그래디언트 방법(예: REINFORCE)과 가치 함수를 결합합니다.

• 액터의 작동 방식은 정책 그래디언트 방법과 유사합니다. 액터는 정책을 구현하여 각 단계에서 정책에 따라 행동을 선택합니다. 기대 수익의 그래디언트를 따라 정책을 업데이트합니다.
• 비평가는 가치 함수를 구현하며, 이는 기준선으로 사용됩니다(이전 섹션에서 논의됨). 이는 훈련을 보다 효율적이고 안정적으로 만드는 데 도움이 됩니다.

정책 그래디언트 방법인 REINFORCE는 원시 수익을 사용하여 각 경로를 따라 그래디언트를 추정합니다. 샘플링 프로세스가 이러한 경로를 생성하기 때문에 수익과 그래디언트에서 큰 분산이 발생할 수 있습니다. 원시 수익 대신 이점 함수를 사용하면 이 문제를 해결할 수 있습니다. 이점 함수는 실제 수익과 예상 수익(즉, 가치 함수) 간의 차이입니다. 액터-비평가 방법은 알고리즘의 한 종류입니다. 비평가가 이점 함수를 사용하여 구현될 때(가장 일반적인 접근 방식), 이를 Advantage actor-critic(A2C)이라고도 합니다.

근접 정책 최적화 (PPO)

복잡한 환경에서 A2C와 같은 액터-비평가 방법만으로는 수익과 그래디언트의 분산을 제어하기에 충분하지 않습니다. 이러한 경우, 각 반복에서 정책이 변경될 수 있는 양을 인위적으로 제한하는 것이 도움이 됩니다. 이는 업데이트된(그래디언트 상승 후) 정책이 이전 정책의 이웃에 위치하도록 강제합니다.

근접 정책 최적화와 같은 방법은 정책 그래디언트에 두 가지 수정을 합니다:

• 장점 함수를 사용하세요. 일반적으로 이 장점 함수는 기준으로 가치 함수를 사용합니다. 이 점에서 A2C 방법과 유사합니다.
• 정책 매개변수가 각 반복에서 변경될 수 있는 양을 제한하세요. 이는 자른 대체 목표 함수를 사용하여 수행됩니다. 알고리즘은 새로운 정책과 이전 정책의 비율이 있어야 하는 범위를 지정합니다. 비율(그래디언트 업데이트 후)이 이러한 미리 정해진 값을 초과하면 범위 내에 있도록 잘립니다.

따라서 PPO는 기본 정책 경량화 방법을 크게 개선하여 복잡한 환경에서의 안정성을 향상시킵니다. 클리핑된 목표 함수는 수익과 기울기의 큰 분산이 정책 업데이트를 불안정하게 만드는 것을 방지합니다. 탐색과 활용의 균형을 이루기 위해 PPO를 수정하여 엔트로피 정규화를 사용할 수도 있습니다. 이는 목표 함수에 엔트로피 항(정책의 엔트로피에 곱해지는 스케일링 매개변수)을 추가함으로써 이루어집니다.

최근 발전

정책 경량화는 RL 문제를 해결하는 데 사용된 초기 방법 중 하나입니다. 빠른 GPU의 출현 이후, 정책 경량화에 현대 ML 기술을 적용하기 위한 다양한 새로운 접근 방식이 제안되었습니다.

그래디언트 부스팅 강화 학습

최근 몇 년 동안, 그라디언트 부스팅과 같은 방법들이 RL 알고리즘에 적용되어 발전되었습니다. 그라디언트 부스팅은 여러 약한 모델의 예측을 결합하여 하나의 강력한 모델을 생성합니다. 이것은 그라디언트 부스트 강화 학습 (GBRL)로 알려져 있습니다. GBRL은 XGBoost와 유사한 파이썬 패키지로, RL 알고리즘에 이러한 기술을 구현합니다.

전이 강화 학습

전이 학습 (TL)은 한 모델이 습득한 지식을 다른 모델의 성능을 향상시키기 위해 적용하는 기술입니다. 전이 학습은 ML 모델을 처음부터 훈련하는 것이 비용이 많이 들기 때문에 유용합니다. TL 접근법은 정책 그라디언트와 함께 사용되어 RL 모델의 성능을 향상시킵니다. 이 접근법은 전이 강화 학습 (TRL)이라고 불립니다.

결론

정책 그라디언트는 RL 문제를 해결하는 데 가장 기본적인 방법 중 하나입니다.

 이 기사에서는 정책 그라디언트의 첫 원리를 소개하고 정책 그라디언트 정리를 어떻게 유도하는지 보여주었습니다. 또한 PyTorch를 사용하여 체육관 환경에서 간단한 그라디언트 기반 알고리즘을 구현하는 방법을 시연했습니다. 마지막으로, 기본 정책 그라디언트 알고리즘의 실제적인 도전과 일반적인 확장에 대해 논의했습니다.

강화 학습과 PyTorch를 활용한 심층 학습을 더 깊게 이해하고 싶다면 다음 강좌를 확인해보세요:

• 강화 학습 트랙 – 가치 기반 방법부터 정책 최적화 기법까지 RL의 기초를 배웁니다.
• PyTorch로 시작하는 딥 러닝 소개 – PyTorch를 활용하여 직접 심층 학습 모델을 구축하는 실무 경험을 쌓을 수 있습니다.