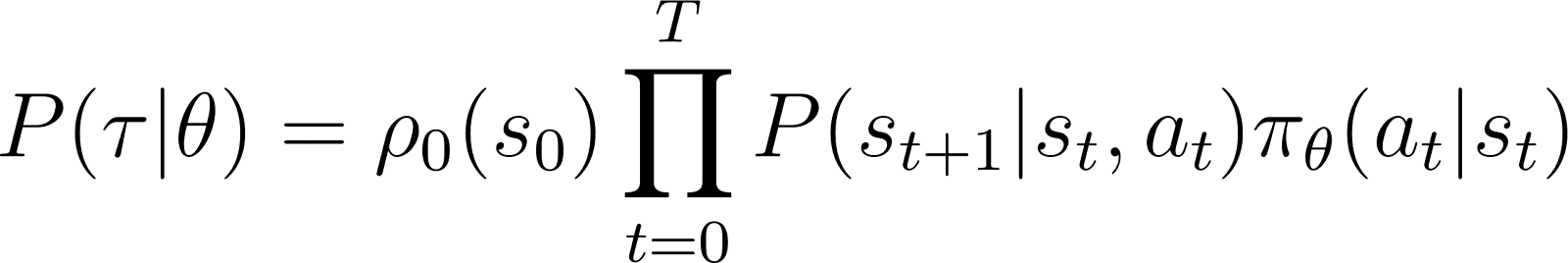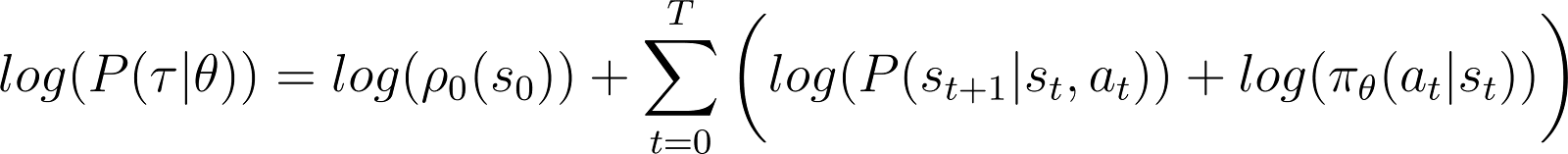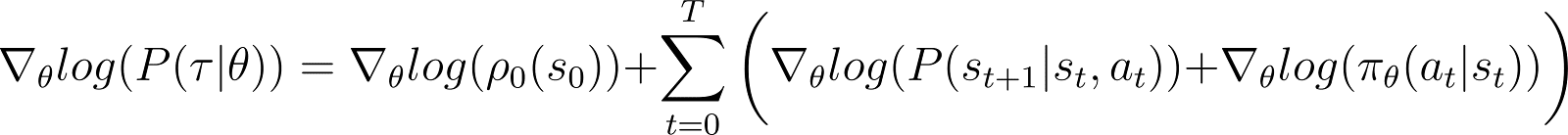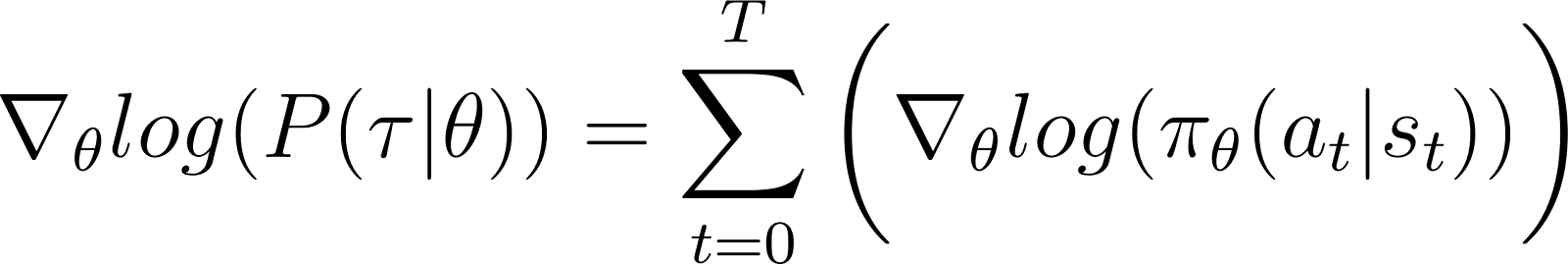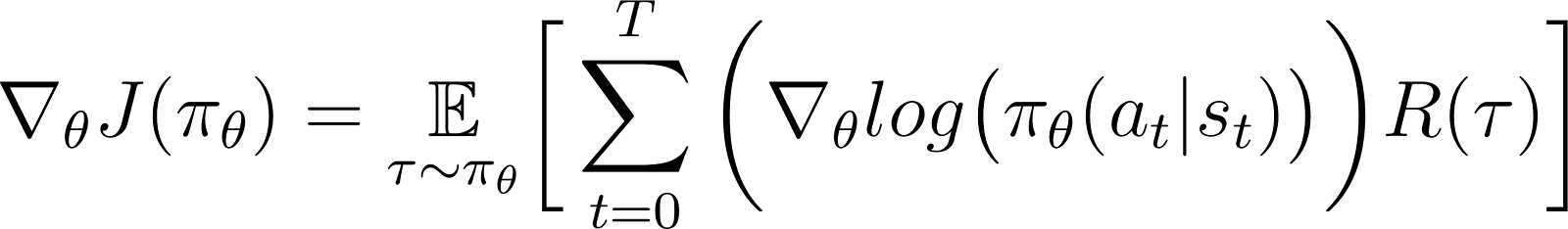強化学習(RL)における方策勾配は、エージェントの方策を直接最適化するアルゴリズムの一種であり、期待される報酬の勾配を方策パラメータに関して推定することである。
このチュートリアルでは、方策勾配定理とその導出を説明し、PyTorchを使用して方策勾配アルゴリズムを実装する方法を示す。
方策勾配定理とは何ですか?
強化学習において、エージェントの方策とは、環境の観測に基づいて行動を決定するために使用するアルゴリズムを指す。RL問題において目標となるのは、エージェントが環境とやり取りすることで獲得する報酬を最大化することである。最大の報酬をもたらす方策が最適方策である。
収益を最大化するために使用されるアルゴリズムの2つの大きなクラスは、方策ベースの方法と価値ベースの方法である。
- ポリシーベースの手法、例えばポリシー勾配アルゴリズムは、期待報酬に対して勾配上昇を適用することによって最適なポリシーを直接学習します。これらは価値関数に依存しません。ポリシーはパラメータ化された形式で表現されます。ポリシーがニューラルネットワークを使用して実装されると、ポリシーのパラメータはネットワークの重みを指します。ネットワークはポリシーパラメータに対する勾配上昇を使用して最適なポリシーを学習します。
- 価値ベースの手法、例えばQ学習は、状態または状態-行動ペアの価値を推定します。 それらは最も高い価値を持つ行動を選択することによってポリシーを間接的に導き出します。最適な価値関数に導くポリシーが最適なポリシーとして選択されます。ベルマン方程式は、最適な状態価値関数と状態-行動価値関数を記述します。
ポリシーグラディエント定理によると、期待リターンの導関数は、リターンとポリシーの対数の導関数(通常、確率分布として表される)の積の期待値です。
ポリシーは通常、パラメータ化された関数としてモデル化されます。ポリシーがニューラルネットワークとしてモデル化される場合、ポリシーパラメータはネットワークの重みを指します。したがって、期待リターン(累積報酬)のポリシーパラメータに関する勾配を計算することは、ポリシーを改善するためにポリシーを更新することにつながります。この勾配は、期待リターンを増加させる方向にポリシーパラメータを反復的に更新するために使用できます。トレーニングは、期待リターンを最大化する最適なポリシーに収束するはずです。
後のセクションでは、この定理を詳しく説明し、どのように導出するかを示します。
ポリシーグラディエントメソッドの利点
ポリシーグラディエントメソッドの主な利点の1つは、伝統的な価値ベースのアプローチが苦戦する複雑なアクションスペースを扱える能力です。
高次元のアクションスペースの取り扱い
価値ベースの手法、例えばQ学習は、すべての可能な行動に対する価値関数を推定することによって機能します。環境の行動空間が連続的または離散的であっても大きい場合、これは困難になります。
ポリシー勾配法はポリシーをパラメータ化し、ポリシーのパラメータに対する累積報酬の勾配を推定します。この勾配を使用して、パラメータを更新することによってポリシーを直接最適化します。したがって、彼らは高次元または連続的な行動空間を効率的に扱うことができます。ポリシー勾配は、人間のフィードバックを利用した強化学習(RLHF)手法の基礎でもあります。
ポリシーをパラメータ化し、勾配に基づいてそのパラメータを調整することによって、ポリシー勾配は連続的かつ高次元の行動を効率的に扱うことができます。この直接的なアプローチは、より良い一般化と柔軟な探索を可能にし、ロボット制御やその他の複雑な環境のようなタスクに適しています。
確率的ポリシーの学習
観察のセットが与えられた場合:
- 確定的ポリシーは、エージェントが取る行動を指定します。
- 確率的ポリシーは、エージェントが各行動を選択する確率を示す一連の行動を与えます。
確率的ポリシーに従うと、同じ観測でも異なる反復で異なる行動を選択することができます。これにより、行動空間の探索が促進され、ポリシーが局所最適解に固執するのを防ぎます。そのため、探索が最大のリターンへと導く経路を発見するのに不可欠な環境では、確率的ポリシーが有用です。
ポリシーベースの手法では、ポリシーの出力が確率分布に変換され、各可能な行動に確率が割り当てられます。エージェントはこの分布をサンプリングして行動を選択し、確率的ポリシーを実装することが可能です。したがって、ポリシーグラディエント法は探索と活用を組み合わせ、複雑な報酬構造を持つ環境で有用です。
ポリシーグラディエント定理の導出
導出に入る前に、証明全体で使用される数学的表記と主要な概念を確立することが重要です。
数学的表記と準備
以前のセクションで述べたように、ポリシーグラディエント定理は、期待収益の導関数が収益とポリシーの対数の導関数の積の期待値であると述べています。
ポリシーグラディエント定理を導出する前に、以下の表記を導入します:
- E[X]は確率変数Xの確率期待値を表します。
- 数学的には、方針は異なる観測に基づいて異なる行動を選択する確率を与える確率行列として表されます。方針は通常、パラメータ化された関数としてモデル化され、パラメータはθで表されます。
- π θ は、θでパラメータ化されたポリシーを指します。実際には、これらのパラメータはポリシーをモデル化するニューラルネットワークの重みです。
- 軌道、τは、通常、ランダムな初期状態から始まり、現在の時間ステップまたは終端状態までの状態のシーケンスを指します。
- ∇θfは、fのパラメータに関する関数の勾配を示します。
- J(πθ)は、エージェントが方針πθに従って達成する期待リターンを指します。これは、勾配上昇の目的関数でもあります。
- 環境は、エージェントの行動に応じて各タイムステップで報酬を与えます。リターンは、初期状態から現在のタイムステップまでの累積報酬を指します。
- R(τ)は、τ軌道上で生成されたリターンを指します。
導出ステップ
私たちは、目的関数の展開から始め、対数微分トリックを使用して、ポリシー勾配定理をどのように導出し証明するかを示します。
目的関数(式1)
ポリシー勾配法における目的関数はリターンです。
Jは、π に基づいた軌跡をたどることで蓄積されます。このポリシーはパラメータθで表現されます。この目的関数は次のように与えられます:
上記の式で:
- 左辺(LHS)はポリシーπθに従って達成される期待リターンです。
- 右辺(RHS)は、ポリシー πθに従って生成される軌跡 τ の期待値です。各ステップで生成される収益の期待値は、軌跡 τ にわたって生成される収益 R(τ)です。
目的関数の微分(式2)
上記の式の両側を(θに関して)微分すると、次のようになります:
期待値の勾配(式3)
期待値(右辺)は、以下の積分として表現できます:
- 軌道をたどる確率τ
- 軌道上で生成されたリターン
したがって、式2の右辺は次のように再記述されます:
積分の勾配は勾配の積分に等しい。したがって、上記の式では、勾配 ∇θを積分記号の下に持ってくることができる。したがって、右辺は次のようになる:
したがって、式2は次のように書き直すことができます:
軌跡の確率(式4)
今、P(τ|θ)、エージェントが軌跡 τ に従う確率を調べます。ポリシーパラメータθを考慮した場合の確率です(したがってポリシーπθ)。軌跡は一連のステップで構成されます。したがって:
- 軌道を取得する確率は、以下の積です:
- すべての個々のステップに従う確率。
- 時間ステップtにおいて、エージェントは状態sから状態st+1に行動atを取る確率は以下の積で与えられます:
- そのポリシーが状態 st で行動 at を予測する確率
- 行動st+1を取った場合の、状態atと状態st
したがって、初期状態s0から始めて、エージェントがポリシーτに基づいて軌跡をたどる確率は、ポリシーπθによって与えられます:
物事を単純化するために、上記のRHSの積を和で表現したいと思います。したがって、上記の方程式の両側に対数を取ります:
対数確率の導関数(方程式5)
今、上記の方程式の対数確率の導関数(θに関して)を取ります。
上記の方程式のRHSでは:
- 最初の項 log ρ0(s0) は θに関して定数です。したがって、その導関数は0です。
- Σ内の最初の項P(st+1|st, at) は、θ およびθ についても独立であり、その導関数も0である。
上記のゼロ項を方程式から取り除くと、以下のようになります(方程式5):
方程式2から思い出してください:
方程式5は、方程式2のRHSの最初の部分の対数を評価します。項の導関数とその対数との関係を示す必要があります。これは連鎖律と対数導関数のトリックを使用して行います。
対数導関数のトリック
私たちは一旦外れ道にそれて微積分のルールを使用して結果を導出し、前の方程式を単純化し、計算方法に適した形に変えます。
微積分では、対数の導関数は次のように表現されます:
したがって、上記の方程式を再配置することにより、xの導関数は、xの対数の導関数を用いて表現できます:
これは時々対数導関数トリックと呼ばれます。
連鎖律
チェーンルールによると、z(y) を関数として、y として、y がそれ自体が関数 θ の関数である場合、y(θ) の導関数は、z を θ に関して以下のように与えられます:
この場合、y(θ)はP(θ)を表し、z(y)はlog(y)を表します。したがって、
連鎖律の適用
微積分からわかることは、d(log(y)) / dy = 1/yです。これを上記の右辺の最初の式に使用します。
yを左辺に移動し、記法を使用します:
y は P(θ) です。したがって、上記の方程式は次のように等価です:
対数微分トリックを適用する
上記の結果は、以下に示す方程式2のRHSの最初の式を与えます。
方程式2のRHSの結果を使用すると、次のようになります:
以下のように、RHS積分の項を再配置します:
最終結果を導出
上記の式には期待値の積分展開が含まれていることに注意してください: ∫P(θ)∇logP(θ) = E[∇logP(θ)]
したがって、上記のRHSは期待値として表現できます。
期待報酬の式に確率の対数の導関数を代入します。
上記の式において、∇logP(θ)の値を式5から代入してください:
これはポリシー勾配定理に基づく報酬関数の勾配の表現です。
ポリシー勾配の直感
ポリシー勾配法は、ポリシーの出力を確率分布に変換します。エージェントはこの分布からサンプリングしてアクションを選択します。ポリシー勾配法はポリシーのパラメータを調整します。これにより、各イテレーションでこの確率分布が更新されます。更新された確率分布は、高い報酬につながるアクションを選ぶ可能性が高くなります。
ポリシー勾配アルゴリズムは、ポリシーのパラメータに関する期待リターンの勾配を計算します。この勾配の方向にポリシーのパラメータを移動させることにより、エージェントはトレーニング中に高い報酬をもたらすアクションを選択する確率を高めます。
基本的に、より良い結果をもたらしたアクションは将来選択される可能性が高くなり、ポリシーを徐々に改善して長期的な報酬を最大化します。
Pythonでのポリシー勾配の実装
ポリシー勾配の基本原則について議論した後、PyTorchとGymnasiumを使用してそれを実装する方法を示します。
環境の設定
最初のステップとして、gymnasiumおよびNumPyやPyTorchなどのいくつかのサポートライブラリをインストールする必要があります。
gymnasiumおよびその依存関係をサーバーまたはローカルマシンにインストールするには、次のコマンドを実行します:
$ pip install gymnasium
Google ColabやDataLabなどのノートブックを使用してインストールするには、次のようにします:
!pip install gymnasium
Python環境内でこれらのパッケージをインポートします:
import torch import torch.nn as nn import torch.optim as optim import torch.nn.functional as F import torch.distributions as distributions import numpy as np import gymnasium as gym
簡単なポリシー勾配エージェントのコーディング
.make()メソッドを使用して環境のインスタンスを作成します。
env = gym.make('CartPole-v1')
他の機械学習手法と同様に、ポリシー勾配エージェントを実装するためにニューラルネットワークを使用します。機械学習。
CartPole-v1は単純な環境なので、64ニューロンを持つ1つの隠れ層を持つ単純なネットワークを設計します。入力層の次元は観測空間の次元と同じです。出力層の次元は環境の行動空間のサイズと同じです。したがって、ポリシーネットワークは観測された状態を行動にマッピングします。入力として観測を受け取ると、ネットワークはポリシーに従って予測された行動を出力します。
以下のコードはポリシーネットワークを実装しています。
class PolicyNetwork(nn.Module): def __init__(self, input_dim, hidden_dim, output_dim, dropout): super().__init__() self.layer1 = nn.Linear(input_dim, hidden_dim) self.layer2 = nn.Linear(hidden_dim, output_dim) self.dropout = nn.Dropout(dropout) def forward(self, x): x = self.layer1(x) x = self.dropout(x) x = F.relu(x) x = self.layer2(x) return x
エージェントのトレーニング
環境は、エージェントの状態と行動に応じて各タイムステップで報酬を与えます。ポリシー勾配アプローチは、累積報酬(リターン)に対して勾配降下を実行することで構成されます。目標は、合計リターンを最大化することです。
エピソード中のリターンを計算するために、そのエピソードのすべてのタイムステップから報酬を蒸留します(割引率を適用)。さらに、リターンを正規化することは、スムーズで安定したトレーニングを確保するのに役立ちます。以下のコードは、これを行う方法を示しています。
def calculate_stepwise_returns(rewards, discount_factor): returns = [] R = 0 for r in reversed(rewards): R = r + R * discount_factor returns.insert(0, R) returns = torch.tensor(returns) normalized_returns = (returns - returns.mean()) / returns.std() return normalized_returns
各反復で、次の手順を実行します:
- 現在のポリシーを使用してエージェントを実行し、
.step()関数を使用します。ポリシーは、各タイムステップで選択したアクションを取る確率を予測します。 - エージェントのアクションに基づいて環境から報酬を受け取ります。
- エージェントが終端状態に到達するまで、段階的な報酬とアクションの対数確率を蓄積します。
以下のコードは、前方パスを実装します:
def forward_pass(env, policy, discount_factor): log_prob_actions = [] rewards = [] done = False episode_return = 0 policy.train() observation, info = env.reset() while not done: observation = torch.FloatTensor(observation).unsqueeze(0) action_pred = policy(observation) action_prob = F.softmax(action_pred, dim = -1) dist = distributions.Categorical(action_prob) action = dist.sample() log_prob_action = dist.log_prob(action) observation, reward, terminated, truncated, info = env.step(action.item()) done = terminated or truncated log_prob_actions.append(log_prob_action) rewards.append(reward) episode_return += reward log_prob_actions = torch.cat(log_prob_actions) stepwise_returns = calculate_stepwise_returns(rewards, discount_factor) return episode_return, stepwise_returns, log_prob_actions
バックプロパゲーションと勾配上昇を使用してポリシーを更新します。
従来の機械学習では:
- 損失は予測と実際の出力との差を指します。
- 勾配降下法を使用して損失を最小限に抑えます。
RL:
- 損失は、勾配降下(または勾配上昇)が適用される数量の代理となります。
- 我々は勾配上昇を用いてリターン(累積報酬)を最大化します。
- 期待されるリターン値は、勾配降下の損失の代理として使用されます。期待されるリターン値は、以下の積で表されます:
- 各ステップで期待されるリターンと
- 各ステップでサンプリングされたアクションを選択する確率。
- バックプロパゲーションを使用して勾配上昇を適用するには、損失の負の値を使用します。
以下のコードは損失を計算します:
def calculate_loss(stepwise_returns, log_prob_actions): loss = -(stepwise_returns * log_prob_actions).sum() return loss
標準の機械学習アルゴリズムと同様に、ポリシーを更新するには、損失関数に関してバックプロパゲーションを実行します。 update_policy()メソッドはcalculate_loss()メソッドを呼び出します。次に、この損失に対してバックプロパゲーションを実行してポリシーパラメータ、つまりポリシーネットワークのモデルウェイトを更新します。
def update_policy(stepwise_returns, log_prob_actions, optimizer): stepwise_returns = stepwise_returns.detach() loss = calculate_loss(stepwise_returns, log_prob_actions) optimizer.zero_grad() loss.backward() optimizer.step() return loss.item()
トレーニングループ
以前に定義された関数を使用してポリシーをトレーニングします。トレーニングを開始する前に、次のものが必要です:
- PolicyNetworkクラスのランダム化されたインスタンスとして初期化されていないポリシー。
- Adamアルゴリズムを使用するオプティマイザ。
- 割引率、学習率、ドロップアウト率、報酬閾値、および最大トレーニングエポック数のハイパーパラメータ。
平均リターンが報酬閾値を超えるまでトレーニングループを繰り返します。各イテレーションでは、次の手順を実行します:
- 各エピソードについて、フォワードパスを1回実行します。アクションの対数確率、段階的なリターン、およびそのエピソードからの総リターンを収集します。エピソードのリターンを配列に蓄積します。
- 対数確率と段階的なリターンを使用して損失を計算します。損失に対してバックプロパゲーションを実行します。オプティマイザを使用してポリシーパラメータを更新します。
N_TRIALSの平均リターンが報酬閾値を超えるかどうかを確認します。
以下のコードはこれらの手順を実装しています:
def main(): MAX_EPOCHS = 500 DISCOUNT_FACTOR = 0.99 N_TRIALS = 25 REWARD_THRESHOLD = 475 PRINT_INTERVAL = 10 INPUT_DIM = env.observation_space.shape[0] HIDDEN_DIM = 128 OUTPUT_DIM = env.action_space.n DROPOUT = 0.5 episode_returns = [] policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT) LEARNING_RATE = 0.01 optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE) for episode in range(1, MAX_EPOCHS+1): episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR) _ = update_policy(stepwise_returns, log_prob_actions, optimizer) episode_returns.append(episode_return) mean_episode_return = np.mean(episode_returns[-N_TRIALS:]) if episode % PRINT_INTERVAL == 0: print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |') if mean_episode_return >= REWARD_THRESHOLD: print(f'Reached reward threshold in {episode} episodes') break
main()関数を呼び出すことでトレーニングプログラムを実行します。このDataLabワークブック
main()
には、方策勾配アルゴリズムの実装が含まれています。直接実行するか、アルゴリズムを修正する出発点として使用できます。
方策勾配法の利点と課題
方策勾配法には、次のようないくつかの利点があります。
- 連続アクション空間の処理:Q学習などの価値ベースの手法は、連続アクション空間では効率が悪いため、全体のアクション空間にわたって値を推定する必要があります。ポリシーグラディエント手法は、期待リターンの勾配を使用してポリシーを直接最適化できます。このアプローチは、連続アクション分布に適しており、ロボット制御などの連続アクション空間に基づくタスクに適しています。
- 確率ポリシー:ポリシーグラディエント手法は、各可能なアクションを選択する確率を提供する確率ポリシーを学習できます。これにより、エージェントはさまざまなアクションを試すことができ、局所最適解に陥るリスクを軽減します。エージェントが最適なポリシーを見つけるためにアクション空間を探索する必要がある複雑な環境で役立ちます。確率的性質は、探索(新しいアクションを試すこと)と活用(最も良く知られているアクションを選択すること)をバランス良く行うのに役立ち、不確実性や希薄な報酬がある環境にとって重要です。
- 直接方策最適化: ポリシーグラデーションは、値関数を使用せずに方策を直接最適化します。連続または高次元の行動空間では、すべての行動に対して値を近似することが計算上高価になる可能性があります。したがって、このような環境では方策ベースの手法がうまく機能します。
多くの利点があるにもかかわらず、ポリシーグラデーション手法にはいくつかの固有の課題があります:
- 勾配推定値の分散が大きい:ポリシー勾配法は行動を確率分布からサンプリングして選択します。実際には、期待収益を推定するために軌跡をサンプリングします。サンプリングプロセスが本質的にランダムであるため、後続の反復で推定される収益は高い分散を持つことがあります。これにより、ポリシーへの更新が反復間で大幅に変動する可能性があり、エージェントが効率的に学習するのを難しくすることがあります。
- トレーニング中の不安定性:
- ポリシー勾配法は学習率などのハイパーパラメータに敏感です。学習率が高すぎると、ポリシーパラメータへの更新が大きすぎて、トレーニングが最適なパラメータを見逃す可能性があります。一方、学習率が小さすぎると収束が遅くなる可能性があります。
- ポリシー勾配法は、探索と利用のバランスを取る必要があります。エージェントが十分に探索しなければ、最適なポリシーの近傍に到達できない可能性があります。逆に、過剰に探索すると、最適なポリシーに収束せず、アクション空間の周りで振動することになります。
- サンプルの非効率性: ポリシー勾配法は、各ポリシーに従って終了まで進行し、各ステップからの報酬を蓄積することでリターンを推定します。したがって、多くのサンプル軌道を引き出すためには、環境との多くの相互作用が必要です。これは、状態やアクション空間が大きい環境では非効率的で高コストです。
安定性のための解決策
不安定性はポリシー勾配法で比較的一般的な問題であるため、開発者はトレーニングプロセスを安定させるためのさまざまな解決策を採用しています。以下に、ポリシー勾配を使用してトレーニングを安定化させるための一般的な解決策を紹介します:
ベースライン関数の使用
非効率的なサンプリングにより、トレーニングの反復中に推定されるリターンの勾配は高い分散を持つ可能性があり、トレーニングが不安定で遅くなることがあります。分散を減少させる一般的なアプローチは、Advantage Actor-Critic (A2C) メソッドのようなベースライン関数を使用することです。このアイデアは、目的関数のために推定されたリターンの代わりに代理(アドバンテージ関数)を使用することです。
アドバンテージは、サンプリングされた軌道からの実際のリターンと初期状態に与えられた期待リターンの差として計算されます。このアプローチでは、状態と状態-アクションペアの期待値として価値関数を使用します。損失を実際のリターンと期待リターンの差として表現することで、A2Cは損失関数の分散、したがって勾配の分散を減少させ、トレーニングをより安定させます。
エントロピー正則化の使用
稀な報酬(非常に少数の状態のみが報酬を与える)を持つ環境では、ポリシーはすぐに決定論的なアプローチを採用します。また、貪欲なアプローチを採用し、すでに探索した経路を利用します。これにより、さらなる探索が妨げられ、しばしば局所最適や非最適ポリシーへの収束につながります。
解決策は、ポリシーがあまりにも決定論的になったときに罰則を課す探索を促進することです。これは、目的関数にエントロピーに基づく項を追加することで行われます。エントロピーは、ポリシーの中のランダム性の量を測定します。エントロピーが大きいほど、エージェントが選択するアクションにランダム性が増します。このエントロピーに基づく項は、エントロピー係数と現在のポリシーのエントロピーとの積です。
エントロピーを目的関数の一部にすることは、搾取と探索のバランスを実現するのに役立ちます。
ポリシーグラディエントの拡張
ポリシーグラディエント法のさまざまな拡張の中で、最も基本的なものの1つがREINFORCEアルゴリズムです。これはポリシーグラディエント定理の直感的な実装を提供し、より高度な技術の基盤となっています。
REINFORCEアルゴリズム
REINFORCEアルゴリズム(モンテカルロリインフォースとも呼ばれます)は、ポリシーグラデント定理の基本的な実装の一つです。これは、モンテカルロ法を使用してリターンとポリシーグラデントを推定します。REINFORCEアルゴリズムに従うと、エージェントは環境からすべてのアクション(初期状態から終端状態まで)を直接サンプルします。これは、TD学習や動的プログラミングのような他の手法とは対照的で、これらの手法は価値関数の推定に基づいてアクションをブートストラップします。
以下にREINFORCEアルゴリズムの基本的なステップを示します:
- ポリシーをランダムなパラメータで初期化する
- 複数のトレーニングエピソードを繰り返す。各エピソードについて:
- 全エピソードの各ステップを以下のように生成する:
- 状態をポリシー関数に渡す。
- ポリシー関数は、各可能なアクションに対する確率を生成します。
- この確率分布からアクションをランダムにサンプリングします。
- エピソード内の各状態について、ステップまでのリターン(割引された累積報酬)を推定します。
- 目的関数の勾配を推定します(ポリシーグラディエント定理に従って)、ステップごとのリターンと各ステップのアクション確率の積として表現されます。
- 勾配を適用してポリシーパラメータを更新します
各ポリシーに対して、単一の軌跡をサンプリングして勾配を推定することができます(上記参照)または、同じポリシーの下でサンプリングされた複数の軌跡に対して勾配を平均化することができます。
アクター-クリティック法
アクター-クリティック法は、ポリシー勾配法(REINFORCEのような)と価値関数を組み合わせています。
- アクターの動作はポリシー勾配法に似ています。アクターはポリシーを実装し、各ステップでポリシーに基づいてアクションを選択します。期待リターンの勾配に従ってポリシーを更新します。
- クリティックは価値関数を実装し、これは基準として使用されます(前のセクションで説明)。これによりトレーニングがより効率的で安定します。
REINFORCEなどのポリシー勾配法は、生のリターンを使用して各軌跡に沿った勾配を推定します。サンプリングプロセスがこれらの軌跡を引くため、リターンと勾配に大きな分散が生じる可能性があります。生のリターンの代わりにアドバンテージ関数を使用することで、この問題を解決できます。アドバンテージ関数は実際のリターンと期待されるリターン(つまり、価値関数)の差です。アクター・クリティック法はアルゴリズムのクラスです。クリティックがアドバンテージ関数を使用して実装される場合(最も一般的なアプローチ)、それはアドバンテージアクター・クリティック(A2C)とも呼ばれます。
Proximal Policy Optimization(PPO)
複雑な環境では、A2Cのようなアクター・クリティック法だけでは、リターンと勾配の分散を制御するのに十分ではありません。そのような場合、各反復でポリシーが変更できる量を人為的に制限することが役立ちます。これにより、更新された(勾配上昇後の)ポリシーが古いポリシーの近くにあるように強制されます。
Proximal Policy Optimizationなどの手法は、ポリシー勾配に2つの修正を加えます。
- アドバンテージ関数を使用します。通常、このアドバンテージ関数は基準として値関数を使用します。これにより、A2Cメソッドに類似しています。
- 各反復でポリシーパラメーターが変更できる量を制限します。これはクリップされた代理目的関数を使用して行われます。アルゴリズムは、新しいポリシーと古いポリシーの比率が存在しなければならない範囲を指定します。勾配更新後の比率がこれらの事前に決定された値を超えると、その比率は範囲内にクリップされます。
したがって、PPOはバニラポリシーグラディエント法を大幅に改善し、複雑な環境における安定性を向上させます。クリップされた目的関数は、リターンとグラディエントの大きな分散がポリシー更新を不安定にするのを防ぎます。探索と活用のバランスを達成するために、エントロピー正則化を使用するようにPPOを修正することも可能です。これは、目的関数にエントロピー項(ポリシーのエントロピーに掛けられたスケーリングパラメータ)を追加することで行います。
最近の進展
ポリシーグラディエントは、RL問題を解決するために使用される最初の手法の一つです。高速GPUの登場以降、ポリシーグラディエントに現代の機械学習技術を適用するためのさまざまな新しいアプローチが提案されています。
勾配ブースト強化学習
近年、勾配ブースティングなどの手法がRLアルゴリズムに適用されるようになってきました。勾配ブースティングは、複数の弱いモデルの予測を組み合わせて単一の強力なモデルを生成します。これは勾配ブースティング強化学習(GBRL)と呼ばれます。GBRLは、これらの手法をRLアルゴリズムに実装したXGBoostに似たPythonパッケージです。
転移強化学習
転移学習(TL)は、1つのモデルで獲得した知識を別のモデルの性能向上に応用する技術です。転移学習は、モデルをゼロからトレーニングするのが高コストであるため役立ちます。TLアプローチはポリシーグラディエントと組み合わせられ、RLモデルの性能を向上させるために使用されています。このアプローチは転移強化学習(TRL)と呼ばれます。
結論
ポリシー勾配は、強化学習問題を解決するための最も基本的なアプローチの一つです。
この記事では、ポリシー勾配の基本原則を紹介し、ポリシー勾配定理の導出方法を示しました。また、Gymnasium環境でPyTorchを使用してシンプルな勾配ベースのアルゴリズムを実装する方法も実演しました。最後に、基本的なポリシー勾配アルゴリズムに対する実際の課題と一般的な拡張について議論しました。
強化学習とPyTorchを用いた深層学習の理解を深めたい方は、これらのコースをチェックしてください:
- 強化学習トラック – 値に基づく手法からポリシー最適化技術まで、RLの基礎を学びます。
- PyTorchによる深層学習入門 – PyTorchを使って実践的な経験を積み、ゼロから深層学習モデルを構築します。
Source:
https://www.datacamp.com/tutorial/policy-gradient-theorem