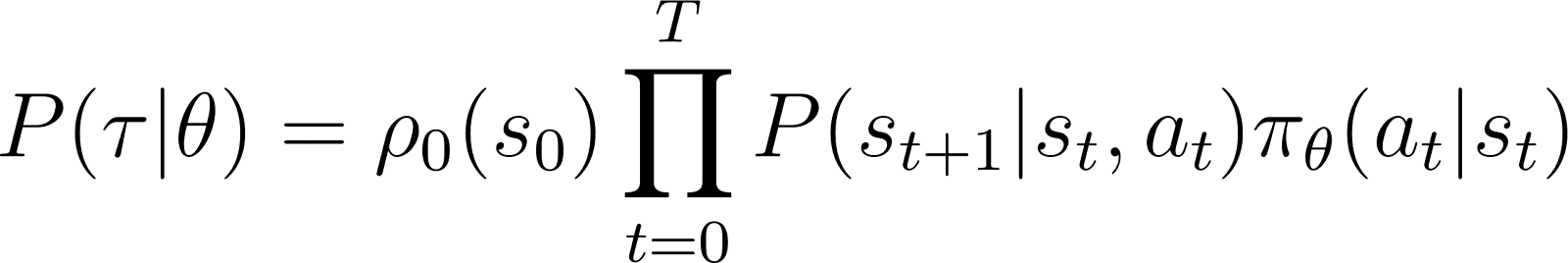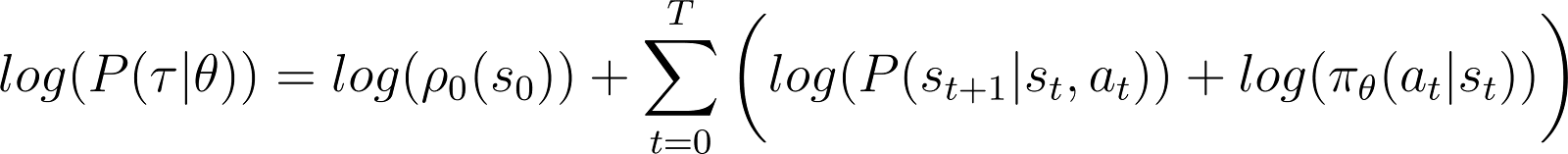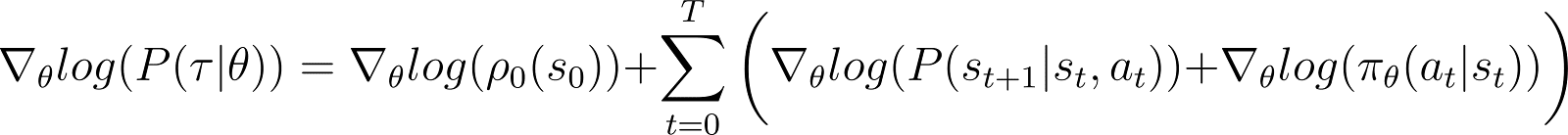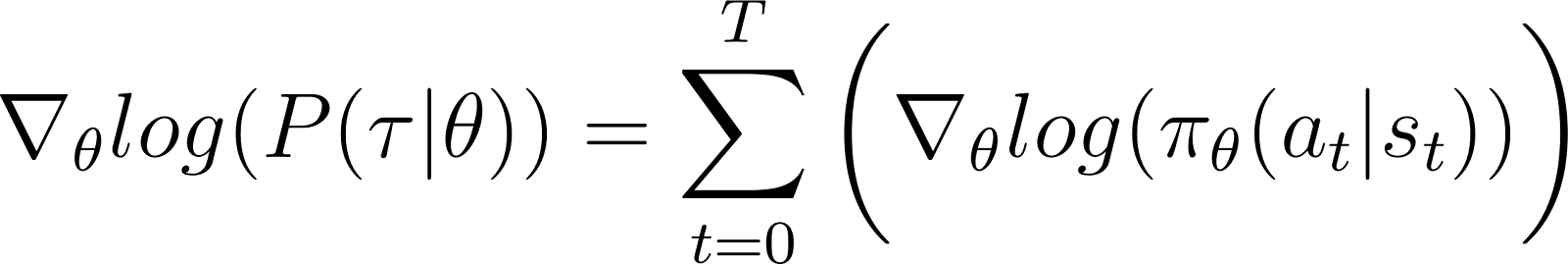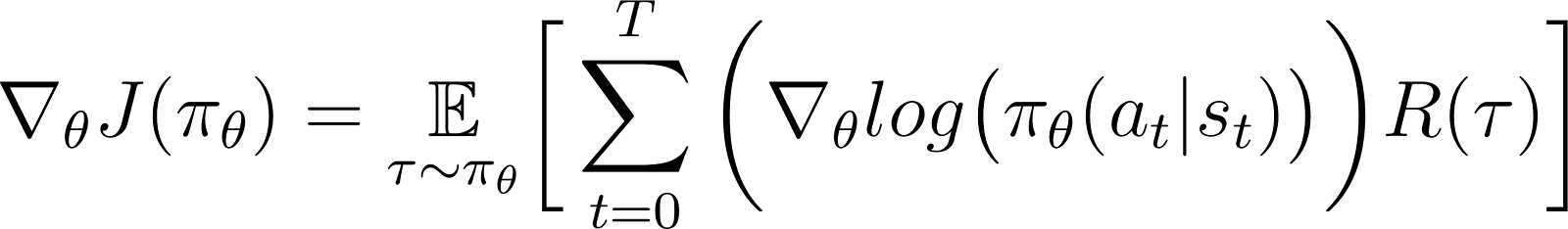تم شرح مبرهنة التدرج السياسي: مقدمة تطبيقية

لماذا استخدام أساليب ميل السياسة؟

إحدى المزايا الرئيسية لأساليب ميل السياسة هي قدرتها على التعامل مع مساحات أفعال معقدة، حيث تواجه النهج التقليدي المعتمد على القيم صعوبات.

التعامل مع مساحات أفعال عالية الأبعاد

تعمل الطرق القائمة على القيم، مثل تعلم الفهم (Q-learning)، من خلال تقدير وظيفة القيمة لجميع الإجراءات الممكنة. يصبح ذلك صعبًا عندما يكون مساحة الإجراءات في البيئة إما مستمرة أو متقطعة ولكن كبيرة.

تقوم طرق تدرج السياسة بتعميم السياسة وتقدير تدرج المكافآت التراكمية بالنسبة للمعلمات السياسية. يستخدمون هذا التدرج لتحسين السياسة مباشرة من خلال تحديث معلماتها. وبالتالي، يمكنهم التعامل بكفاءة مع مساحات الإجراءات عالية الأبعاد أو المستمرة. تعتبر تدرجات السياسة أساسًا أيضًا لطرق تعلم التعزيز باستخدام تغذية راجعة من البشر (RLHF).

من خلال تعميم السياسة وضبط معلماتها بناءً على التدرجات، يمكن لتدرجات السياسة التعامل بكفاءة مع الإجراءات المستمرة وذات الأبعاد العالية. يتيح هذا النهج المباشر التعميم الأفضل والاستكشاف المرن أكثر، مما يجعله مناسبًا تمامًا للمهام مثل التحكم في الروبوتات وبيئات أخرى معقدة.

تعلم السياسات العشوائية

بناءً على مجموعة من الملاحظات:

• تحدد السياسة التحديدية الإجراء الذي يتخذه الوكيل.
• تعطي السياسة الاحتمالية مجموعة من الإجراءات واحتمالية اختيار الوكيل لكل إجراء.

عند اتباع سياسة احتمالية، يمكن أن تؤدي نفس الملاحظة إلى اختيار إجراءات مختلفة في تكرارات مختلفة. يعزز ذلك استكشاف مساحة الإجراءات ويمنع السياسة من العلق في النقاط المحلية الأمثل. وبسبب ذلك، تكون السياسات الاحتمالية مفيدة في البيئات حيث يكون الاستكشاف ضروريًا لاكتشاف المسار الذي يؤدي إلى أقصى عوائد.

في الطرق القائمة على السياسة، يتم تحويل إخراج السياسة إلى توزيع احتمالي، مع تخصيص احتمالية لكل إجراء ممكن. يختار الوكيل إجراءً عن طريق أخذ عينة من هذا التوزيع، مما يجعل من الممكن تنفيذ سياسة احتمالية. وبالتالي، تجمع طرق التدرج في السياسة بين الاستكشاف والاستغلال، مما يكون مفيدًا في البيئات ذات الهياكل المعقدة للمكافآت.

اشتقاق نظرية تدرج السياسة

قبل الانغماس في الاشتقاق، من المهم تحديد العلامات الرياضية والمفاهيم الرئيسية المستخدمة طوال البرهان.

العلامات الرياضية والمقدمات

كما ذُكر في القسم السابق، تقول نظرية تدرج السياسة أن مشتقة العائد المتوقع هي توقع حاصل ضرب العائد ومشتقة اللوغاريتم للسياسة.

قبل استنباط نظرية تدرج السياسة، نقدم العلامات التالية:

• E[X] تشير إلى التوقع الاحتمالي لمتغير عشوائي X.
• رياضيًا، تُعبّر السياسة عن مصفوفة احتمالات تُعطي احتمال اختيار أفعال مختلفة استنادًا إلى ملاحظات مختلفة. تُنمذج السياسة عادةً كدالة معلمة، حيث تُمثل المعلمات بشكل θ.
• π_θ يشير إلى سياسة معلمة بواسطة θ. في الممارسة، هذه المعلمات هي أوزان الشبكة العصبية التي تقوم بنمذجة السياسة. 
• المسار، τ، يشير إلى تسلسل من الحالات، عادة ما يبدأ من حالة أولية عشوائية حتى الخطوة الزمنية الحالية أو الحالة النهائية.
• ∇_θf يشير إلى التدرج لوظيفة f بالنسبة للمعلمة(المعلمات) θ.
• J(π_θ)يشير إلى العائد المتوقع الذي يحققه الوكيل باتباع السياسة π_θ. وهذه أيضًا الدالة الهدف لصعود التدرج.
• تقدم البيئة مكافأة في كل فترة زمنية، اعتمادًا على إجراء العميل. يشير العائد إلى المكافآت التراكمية من الحالة الابتدائية إلى الفترة الزمنية الحالية.
• R(τ) يشير إلى العائد الذي تم تحقيقه على مدار τ.

خطوات الاشتقاق

نوضح كيفية استقرار وإثبات نظرية تدرج السياسات من المبادئ الأولية، بدءًا من توسيع الدالة الهدف واستخدام خدعة الاشتقاق اللوغاريتمي.

الدالة الهدف (المعادلة 1)

الدالة الهدف في طريقة تدرج السياسة هي العائد

لقد تم تراكم من خلال اتباع المسار بناءً على السياسة π المعبرة بمصطلحات المعلمات θ. تُعطى هذه الوظيفة الهدف على النحو التالي: 

في المعادلة أعلاه:

• الجانب الأيسر (LHS) هو العائد المتوقع الذي يتم تحقيقه باتباع السياسة π_θ.
• الجانب الأيمن (RHS) هو التوقع (على مدار τ المُولد باتباع السياسة π_θ في كل خطوة) للعوائد R(τ) المولدة على مدار τ.   

التفاضل لدالة الهدف (المعادلة 2)

تفضيلا (بالنسبة إلى θ) كلتي الجانبين للمعادلة أعلاه يعطي:

الميل للتوقع (المعادلة 3)

يمكن تعبير التوقع (على الجانب الأيمن) عن طريق التكامل على حاصل ضرب:

• احتمال اتباع مسار τ
• تمت إعادة توليد العوائد التي تم تحقيقها على مدار τ

بالتالي، يتم إعادة صياغة الجزء الأيمن من المعادلة 2 على النحو التالي:

ميل التكامل يساوي التكامل من الميل. لذلك، في التعبير أعلاه، يمكننا جلب الميل ∇_θ تحت علامة التكامل. لذلك، تصبح الجهة اليمنى: 

وبالتالي، يمكن إعادة صياغة المعادلة 2 على النحو التالي:

احتمالية المسار (المعادلة 4)

نلقي الآن نظرة أقرب على P(τ|θ)، احتمالية أن يتبع العامل المسار τ معلمات السياسة θ (وبالتالي السياسة π_θ). يتكون المسار من مجموعة من الخطوات. وبالتالي:

• احتمال الحصول على مسار τ هو ناتج ضرب:
• احتمال اتباع جميع الخطوات الفردية.

• في الخطوة الزمنية t, ينتقل الوكيل من الحالة s إلى الحالة s_t+1 عن طريق اتباع الإجراء a_t. إحتمال حدوث هذا الأمر يعطى حاصل ضرب:
• احتمالية أن يتنبأ السياسة بالإجراء أ_ل في الحالة س_ت
• إحتمال الوصول إلى الحالة s_t+1 بعد اتخاذ الإجراء a_t وفي الحالة s_t

وبالتالي، ابتداءً من الحالة الابتدائية s₀، يتم تحديد احتمالية تبع الوكيل لمسار τ بناءً على السياسة π_θ على النحو التالي:

لتبسيط الأمور، نود تعبير المنتج في الجانب الأيمن من الفرقة السابقة على شكل مجموعة. لذلك، نأخذ اللوغاريتم على كلا الجانبين من المعادلة أعلاه:

المشتقة للإحتمالية باللوغاريتم (المعادلة 5) 

نأخذ الآن المشتقة (بالنسبة إلى θ) للإحتمالية باللوغاريتم في المعادلة أعلاه. 

على الجانب الأيمن من المعادلة أعلاه: 

• المصطلح الأول log ρ₀(s₀) هو ثابت بالنسبة إلى θ. لذا مشتقته هي 0.
• المصطلح الأول داخل الجمع P(s_t+1|s_t, a_t) مستقل أيضًا من θ ومشتقته بالنسبة لـ θ هي أيضًا 0. 

بعد إزالة المصطلحات الصفرية أعلاه من المعادلة، نبقى مع (المعادلة 5):

تذكر من المعادلة 2 أن:

المعادلة 5 تقوم بحساب اللوغاريتم للجزء الأول من RHS للمعادلة 2. نحتاج إلى ربط مشتقة المصطلح بلوغاريتمه. نقوم بذلك باستخدام قاعدة السلسلة وخدعة اللوغاريتم للمشتقة.

خدعة اللوغاريتم للمشتقة

نأخذ مسارًا آخر ونستخدم قواعد الحساب لاستنتاج نتيجة، سنستخدمها لتبسيط المعادلة السابقة وجعلها مناسبة للأساليب الحسابية.

في الحساب، يمكن التعبير عن مشتقة اللوغاريتم على النحو التالي:

وبالتالي، من خلال إعادة ترتيب المعادلة أعلاه، يمكن تعبير المشتقةx بالنسبة لمشتق اللوغاريتم من x:

ويُطلق عليها أحيانًا خدعة المشتق المتعامد.

قاعدة السلسلة

وفقًا لقاعدة السلسلة، مع توفير z(y) كدالة لـ y، حيث y هو دالة لـ θ، y(θ)، يتم توفير مشتق z بالنسبة إلى θ على النحو التالي:

في هذه الحالة، y(θ) تعني P(θ) و z(y) تعني log(y). وبالتالي، 

تطبيق قاعدة السلسلة

نحن نعرف من الحساب التفاضلي أن d(log(y)) / dy = 1/y. استخدم هذا في التعبير الأول للجانب الأيمن أعلاه. 

انقل y إلى الجانب الأيسر واستخدم علامة الـ :

y تمثل P(θ). لذلك، المعادلة أعلاه مكافئة ل:

تطبيق خدعة المشتقة اللوغاريتمية

النتيجة أعلاه تعطي التعبير الأول لجانب الحقل من المعادلة 2 (الموضحة أدناه).

باستخدام النتيجة في الجانب الأيمن من المعادلة 2، نحصل على:

نعيد ترتيب الحدود تحت التكامل في الجانب الأيمن كما هو موضح أدناه:

استنتاج النتيجة النهائية

لاحظ أن التعبير أعلاه يحتوي على توسيع متكامل للتوقع: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

وبالتالي، يمكن تعبير RHS أعلاه على أنه التوقع:

نقوم بتبديل المشتقة من سجل الاحتمال في تعبير المكافأة المتوقعة:

في المعادلة أعلاه، قم بتعويض قيمة ∇logP(θ) من المعادلة 5 للحصول على:

هذا هو التعبير عن التدرج لدالة الأجر وفقا لنظرية تدرج السياسة.

الحدس وراء تدرج السياسة

تحويل طرق تدرج السياسة إلى توزيع احتمالي. يقوم العامل بعينات من هذا التوزيع لاختيار إجراء. تقوم طرق تدرج السياسة بضبط معلمات السياسة. يؤدي ذلك إلى تحديث هذا التوزيع الاحتمالي في كل تكرار. يزيد التوزيع الاحتمالي المحدث من احتمالية اختيار الإجراءات التي تؤدي إلى مكافآت أعلى. 

يحسب خوارزمية تدرج السياسة تدرج العائد المتوقع بالنسبة لمعلمات السياسة. من خلال نقل معلمات السياسة في اتجاه هذا التدرج، يزيد العامل من احتمالية اختيار إجراءات تؤدي إلى مكافآت أعلى خلال التدريب. 

بشكل أساسي، تصبح الإجراءات التي أدت إلى نتائج أفضل أكثر احتمالية لتكون مختارة في المستقبل، مما يحسن تدريجيًا السياسة لتعظيم المكافآت على المدى الطويل.

تنفيذ تدرجات السياسة في بايثون

بعد مناقشة المبادئ الأساسية للتدريبات السياسية، سنقدم كيفية تنفيذها باستخدام PyTorch و Gymnasium.

إعداد البيئة

كخطوة أولى، نحتاج إلى تثبيت gymnasium وبعض المكتبات الداعمة مثل NumPy و PyTorch.

لتثبيت gymnasium وتبعياته على خادم أو جهاز محلي، قم بتشغيل:

$ pip install gymnasium 

للتثبيت باستخدام دفتر ملاحظات مثل Google Colab أو DataLab، استخدم:

!pip install gymnasium

يمكنك استيراد هذه الحزم داخل بيئة Python:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

تشفير وكود وكيل تدريبات السياسة البسيط

إنشاء مثيل للبيئة باستخدام الطريقة .make().التحليل.

env = gym.make('CartPole-v1')

كما هو الحال مع طرق تعلم الآلة الأخرى، نستخدم شبكة عصبونية لتنفيذ عامل تعزيز السياسة.

CartPole-v1 هي بيئة بسيطة، لذا نقوم بتصميم شبكة بسيطة تحتوي على طبقة مخفية تحتوي على 64 خلية عصبية. يكون حجم الطبقة الداخلية يساوي أبعاد مساحة الملاحظة. حجم الطبقة الناتجة يساوي حجم مساحة الإجراءات في البيئة. بالتالي، تقوم الشبكة السياسية بتعيين الحالات المرصودة إلى إجراءات. باستخدام الملاحظة كإدخال، تخرج الشبكة بالإجراء المتوقع وفقًا للسياسة.

الكود أدناه ينفذ الشبكة السياسية:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

تدريب العامل

تعطي البيئة مكافأة في كل الخطوات بناءً على حالة العامل والإجراء. يتكون نهج التدرج في السياسة من تشغيل التدرج على المكافآت التراكمية (العائد). الهدف هو تعظيم العائد الإجمالي.

لحساب العائد في حلقة، يتم تجميع المكافآت (مع عامل الخصم) من جميع الخطوات في تلك الحلقة. بالإضافة إلى ذلك، يعد تقليل حجم العائد مفيدًا لضمان تدريب سلس ومستقر. الكود أدناه يوضح كيفية القيام بذلك:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

في كل تكرار من عملية التمرير الأمامي، نقوم بالخطوات التالية:

• تشغيل الوكيل بناءً على السياسة الحالية باستخدام دالة .step()، حيث تتنبأ السياسة باحتمالية اتخاذ الإجراء المختار في كل خطوة زمنية.
• تلقي المكافأة من البيئة بناءً على إجراء الوكيل.
• تجميع المكافآت خطوة بخطوة واحتمالات سجلات الإجراءات حتى يصل الوكيل إلى حالة نهائية.

الكود أدناه ينفذ عملية التمرير الأمامي:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

استخدام الانتشار العكسي وصعود التدرج لتحديث السياسة

في التعلم الآلي التقليدي:تعلم الآلة:

• تشير الخسارة إلى الفرق بين الناتج المتوقع والناتج الفعلي.
• نقوم بتقليل الخسارة باستخدام الانحدار التدرجي.

في التعلم المعزز:

• الخسارة هي بروكسي للكمية التي يجب تطبيق انحدار التدرج (أو الصعود) عليها.
• نحن نقوم بتحقيق أقصى عائد (المكافآت التراكمية) باستخدام ارتفاع التدرج.
• قيمة العائد المتوقع تُستخدم كبديل للخسارة في انحدار التدرج. قيمة العائد المتوقع هي ناتج:
• العوائد المتوقعة من كل خطوة مع
• احتمالية اختيار الإجراء المُحدد في كل خطوة.
• لتطبيق ارتفاع التدرج باستخدام الانحدار للخلف، نستخدم السالب من الخسارة.

الشيفرة أدناه تحسب الخسارة:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

مماثل لخوارزميات التعلم الآلي القياسية، لتحديث السياسة، يتم تشغيل الانحدار للخلف بالنسبة لوظيفة الخسارة. الطريقة update_policy() أدناه تستدعي الطريقة calculate_loss(). ثم تقوم بتشغيل الانحدار للخلف على هذه الخسارة لتحديث معلمات السياسة، أي وزن النموذج لشبكة السياسة.

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

حلقة التدريب

نستخدم الوظائف المعرفة سابقًا لتدريب السياسة. قبل بدء التدريب، نحتاج:

• سياسة غير مدربة مبدئيًا كنسخة معتمدة عشوائية من فئة PolicyNetwork.
• محسن يستخدم خوارزمية Adam.
• معلمات فوقية لعامل الخصم، معدل التعلم، معدل الانسحاب، حد المكافأة، وأقصى عدد من حلقات التدريب.

نكرر الحلقة التدريبية حتى يتجاوز المتوسط العائد حد المكافأة. في كل تكرار، ننفذ الخطوات التالية:

• لكل حلقة، قم بتشغيل المرور الأمامي مرة واحدة. اجمع الاحتمالية المسجلة للإجراءات، والعوائد التدريجية، والعائد الإجمالي من تلك الحلقة. اجمع العوائد الحلقية في مصفوفة.
• احسب الخسارة باستخدام الاحتماليات المسجلة والعوائد التدريجية. قم بتشغيل التداول على الخسارة. استخدم المحسن لتحديث معلمات السياسة.
• تحقق مما إذا كان متوسط العائد على N_TRIALS يتجاوز حد المكافأة.

الشيفرة أدناه تنفذ هذه الخطوات:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

قم بتشغيل برنامج التدريب عن طريق استدعاء main() الدالة: وظيفة:

main()

يحتوي هذا الدليل الإلكتروني على تنفيذ خوارزمية الميل السياسي المذكورة أعلاه. يمكنك تشغيله مباشرة أو استخدامه كنقطة انطلاق لتعديل الخوارزمية.

مزايا وتحديات طرق الميل السياسي

تقدم طرق الميل السياسي العديد من المزايا، مثل:

• معالجة فضاءات العمل المستمرة: الأساليب القائمة على القيم (مثل تعلم Q) غير كفءة مع فضاءات العمل المستمرة لأنها تحتاج إلى تقدير القيم على مدى الفضاء الكلي للأفعال. يمكن لأساليب تدريج السياسات تحسين السياسة مباشرة باستخدام التدرج في العوائد المتوقعة. هذا النهج يعمل بشكل جيد مع توزيعات الأفعال المستمرة. وبالتالي، تعد أساليب تدريج السياسات مناسبة للمهام مثل التحكم الروبوتي المعتمدة على فضاءات الأفعال المستمرة.
• السياسات العشوائية: يمكن لأساليب تدريج السياسات تعلم السياسات العشوائية – التي تعطي احتمالية اختيار كل إجراء ممكن. يتيح ذلك للوكيل تجربة مجموعة متنوعة من الإجراءات ويقلل من خطر الوقوع في النقاط المحلية المثلى. يساعد في البيئات المعقدة حيث يحتاج الوكيل إلى استكشاف فضاء الأفعال للعثور على السياسة الأمثل. الطبيعة العشوائية تساعد في تحقيق توازن بين الاستكشاف (تجربة إجراءات جديدة) والاستغلال (اختيار أفضل الإجراءات المعروفة)، وهو أمر حاسم للبيئات ذات الحالات المتغيرة أو العوائد النادرة.
• التحسين المباشر للسياسات: تحسين تدفقات السياسة يحسن السياسة مباشرة بدلاً من استخدام وظائف القيمة. في الفضاءات العمل المستمرة أو عالية الأبعاد ، يمكن أن يصبح تقريب القيم لكل إجراء مكلفًا حسابيًا. وبالتالي ، تؤدي الطرق القائمة على السياسة بشكل جيد في مثل هذه البيئات. 

على الرغم من مزاياها العديدة ، فإن طرق تدفق السياسة تواجه بعض التحديات الجوهرية:

• تباين عالٍ في تقديرات الميل الحاد: تقوم طرق ميل السياسة باختيار الإجراءات عن طريق أخذ عينات من توزيع احتمالية. في الواقع، تأخذ عينة من المسار لتقدير العائد المتوقع. نظرًا لأن عملية الأخذ عينات تكون عشوائية بشكل جوهري، يمكن أن تكون التقديرات للعوائد في التكرارات التالية ذات تباين عالٍ. يمكن أن يجعل ذلك من الصعب على العامل التعلم بكفاءة لأن التحديثات على السياسة قد تتقلب بشكل كبير بين التكرارات. 
• عدم الاستقرار أثناء التدريب: 
• طرق ميل السياسة حساسة للمعلمات الفرعية مثل. إذا كان معدل التعلم مرتفعًا جدًا، فإن التحديثات على معلمات السياسة يمكن أن تكون كبيرة جدًا، مما يتسبب في فشل التدريب في الوصول إلى المعلمات الأمثل. من ناحية أخرى، إذا كان معدل التعلم صغيرًا جدًا، فإن التقارب قد يكون بطيئًا. 
• طرق تدريب السياسات تحتاج إلى تحقيق توازن بين استكشاف البيئة واستغلالها. إذا لم يقم الوكيل بالاستكشاف بما فيه الكفاية، قد لا يصل إلى جوار السياسة الأمثل. وعلى الجانب الآخر، إذا قام بالاستكشاف بشكل زائد، فلن يتقرب من السياسة الأمثل وسيتذبذب حول مجال الإجراءات.
• نقص الفعالية في العينة: تقوم طرق تدريب السياسات بتقدير العائد عن طريق متابعة كل سياسة حتى الانتهاء وتجميع المكافآت من كل خطوة. وبالتالي، فإنها تحتاج إلى العديد من التفاعلات مع البيئة لرسم عدد كبير من المسارات العينية. وهذا غير فعال ومكلف للبيئات ذات المساحات الكبيرة للحالة أو الإجراء.

حلول للثبات

نظرًا لكون عدم الاستقرار مشكلة شائعة نسبيًا في طرق تدريب السياسات، اعتمد المطورون حلولًا مختلفة لتثبيت عملية التدريب. فيما يلي، نقدم الحلول الشائعة لتثبيت التدريب باستخدام السياسات التي تعتمد على السياسات:

استخدام وظائف القاعدة.

نظرًا للعينات غير الفعالة، يمكن أن تكون الميلات للعوائد المقدرة خلال التكرارات التدريبية لها تباينًا عاليًا، مما يجعل التدريب غير مستقر وبطيء. يُعد استخدام الوظائف الأساسية، مثل طريقة الفاعل-القاضي (A2C)، نهجًا شائعًا لتقليل التباين. الفكرة تتمثل في استخدام بروكسي (وظيفة الميزة) بدلاً من العائد المقدر لوظيفة الهدف.

يتم حساب الميزة كفارق بين العائد الفعلي من المسار المعاين والعائد المتوقع نظرًا للحالة الابتدائية. يشمل هذا النهج استخدام وظيفة القيم كالقيمة المتوقعة للحالات وأزواج الحالة-الفعل. من خلال تمثيل الخسارة كفارق بين العائد الفعلي والعائد المتوقع بدلاً من العوائد بمفردها، يقلل A2C من التباين في وظيفة الخسارة وبالتالي في الميلات، مما يجعل التدريب أكثر استقرارًا.

استخدام تنظيم الانحراف

في بعض البيئات، مثل تلك التي تحتوي على مكافآت نادرة (حيث تعطي عدد قليل جدًا من الحالات مكافأة)، تعتمد السياسة بسرعة على نهج محدد. كما تعتمد على نهج جشع وتستغل المسارات التي استكشفتها بالفعل. يمنع هذا الأمر المزيد من الاستكشاف وغالبًا ما يؤدي إلى التقارب على النقاط المحلية الأمثل والسياسات غير الأمثل.

الحل هو تشجيع استكشاف تأثير تعقيم السياسة عندما يصبح محددًا للغاية. يتم ذلك عن طريق إضافة مصطلح يعتمد على التشويش إلى وظيفة الهدف. يقيس التشويش كمية العشوائية في السياسة. كلما زاد التشويش، زادت العشوائية في الإجراءات التي يختارها الوكيل. يكون هذا المصطلح الذي يعتمد على التشويش هو ناتج ضرب معامل التشويش وتشويش السياسة الحالي.

جعل التشويش جزءًا من وظيفة الهدف يساعد على تحقيق توازن بين استغلال البيئة واستكشافها.

تمديدات مبدأ المنحى السياسي

من بين التمديدات المختلفة لطرق مبدأ المنحى السياسي، أحد أكثرها أساسية هو خوارزمية REINFORCE. إنها توفر تنفيذًا مباشرًا لنظرية مبدأ المنحى السياسي وهي الأساس لتقنيات أكثر تقدمًا.

خوارزمية REINFORCE

خوارزمية REINFORCE، المعروفة أيضًا باسم مونتي كارلو رينفورس، هي واحدة من التنفيذات الأساسية لنظرية تدرج السياسة. إنها تستخدم طرق مونتي كارلو لتقدير العوائد وتدرجات السياسة. عند اتباع خوارزمية REINFORCE، يقوم الوكيل بسحب عينات مباشرة لجميع الإجراءات (من الحالة الابتدائية إلى الحالة النهائية) من البيئة. يتناقض هذا مع طرق أخرى مثل TD-Learning والبرمجة الديناميكية، التي تعتمد إجراءاتها على تقديرات وظيفة القيمة.

أدناه، نقدم الخطوات الأساسية لخوارزمية REINFORCE:

• بادر بتهيئة السياسة بمعلمات عشوائية
• كرر حلقات التدريب المتعددة. لكل حلقة:
• أنشئ كل خطوة من الحلقة بأكملها على النحو التالي:
• قم بتمرير الحالة إلى وظيفة السياسة.
• تقوم وظيفة السياسة بتوليد احتمالات لكل إجراء ممكن.
• اختيار إجراء عشوائي من هذا التوزيع الاحتمالي.
• لكل حالة في الحلقة، قم بتقدير العوائد (المكافآت التراكمية المخفضة) حتى الخطوة.
• قم بتقدير ميل الدالة الهدف (وفقًا لنظرية ميل السياسة)، المعبّر عن حاصل ضرب العوائد الخطوية واحتماليات الإجراء لكل خطوة.
• قم بتحديث معلمات السياسة عن طريق تطبيق التدرجات

لكل سياسة، يمكنك أخذ مسار واحد لتقدير التدرج (كما هو موضح أعلاه) أو متوسط التدرج عبر عدة مسارات تم توليدها بنفس السياسة.

أساليب الممثل-النقاد

تجمع أساليب الممثل-النقاد بين أساليب تدرج السياسة (مثل REINFORCE) مع وظائف القيمة.

• عمل الممثل مشابه لأساليب تدرج السياسة. ينفذ الممثل السياسة، باختيار إجراءات في كل خطوة بناءً على السياسة. يُحدث السياسة عن طريق اتباع التدرج في العائد المتوقع.
• النقاد ينفذ وظيفة القيمة، التي تُستخدم كقاعدة مرجعية (تم مناقشتها في القسم السابق). هذا يساعد في جعل التدريب أكثر كفاءة واستقرارًا.

أساليب تدرج السياسة مثل REINFORCE تقدر التدرجات على طول كل مسار باستخدام العائد الخام. نظرًا لأن عملية السحب تستخرج هذه المسارات، يمكن أن تؤدي إلى تباينات كبيرة في العوائد والتدرجات. استخدام دالة الميزة بدلاً من العوائد الخام يحل هذه المشكلة. دالة الميزة هي الفرق بين العائدات الفعلية والمتوقعة (أي، دالة القيمة). أساليب الممثل-الناقد هي فئة من الخوارزميات. عندما يتم تنفيذ الناقد باستخدام دالة الميزة (النهج الأكثر شيوعًا)، يُطلق عليه أيضًا اسم ممثل-ناقد الميزة (A2C). 

تحسين السياسة القريب (PPO)

في البيئات المعقدة، فإن أساليب الممثل-الناقد مثل A2C وحدها ليست كافية للتحكم في التباين في العوائد والتدرجات. في مثل هذه الحالات، يساعد تقييد الكمية التي يمكن أن تتغير بها السياسة في كل تكرار بشكل مصطنع. هذا يجبر السياسة المحدثة (بعد صعود التدرجات) على أن تكون في جوار السياسة القديمة. 

تقوم أساليب مثل تحسين السياسة القريب بإجراء تعديلين على تدرجات السياسة:

• استخدم وظيفة ميزة. عادةً، تستخدم هذه الوظيفة ميزة وظيفة القيم كقيمة أساسية. في هذا الصدد، فهي مشابهة لطرق A2C.
• قيد مقدار السماح لتغيير معلمات السياسة في كل تكرار. يتم ذلك باستخدام وظيفة هدف بديلة مقصوصة. يحدد الخوارزمية نطاقًا يجب أن يكون معدل السياسة الجديد إلى السياسة القديمة ضمنه. عندما يتجاوز المعدل (بعد تحديث التدرج) هذه القيم المحددة مسبقًا، يتم قصه ليكون ضمن النطاق. 

لذلك، تعمل PPO على تحسين طرق تدرجات السياسة التقليدية بشكل كبير، مما يعزز الاستقرار في البيئات المعقدة. تمنع وظيفة الهدف المقصوصة التباينات الكبيرة في العوائد والتدرجات من زعزعة تحديثات السياسة. لتحقيق التوازن بين الاستكشاف والاستغلال، من الممكن أيضًا تعديل PPO لاستخدام تنظيم الانتروبيا. يتم ذلك من خلال إضافة مصطلح انتروبيا (معامل مقياس مضروب في انتروبيا السياسة) إلى وظيفة الهدف.

التطورات الأخيرة

تعتبر تدرجات السياسة من بين أقدم الطرق المستخدمة لحل مشكلات التعلم المعزز. بعد ظهور وحدات معالجة الرسوميات السريعة، تم اقتراح مجموعة متنوعة من الأساليب الجديدة لتطبيق تقنيات التعلم الآلي الحديثة على تدرجات السياسة.

التعلم المعزز المدعوم بالتدرجات

في السنوات الأخيرة، تم تحقيق تقدم في تطبيق طرق مثل تعزيز التدرج على خوارزميات RL. تجمع تقنية تعزيز التدرج بين التنبؤات من عدة نماذج ضعيفة لإنشاء نموذج قوي واحد. يُشار إلى ذلك بـ تعزيز التدرج للتعلم التقويمي (GBRL). GBRL هو حزمة برمجية بلغة Python تشبه XGBoost وتنفذ هذه التقنيات لخوارزميات RL.

تعلم التحويل للتعلم التقويمي 

تعلم التحويل (TL) هو تقنية يتم فيها تطبيق المعرفة المكتسبة من نموذج واحد لتحسين أداء نموذج آخر. يكون تعلم التحويل مفيدًا لأن تدريب نماذج ML من البداية مكلف. وقد تم استخدام أساليب TL مع مرتبات السياسات لتحسين أداء نماذج RL. يُطلق على هذا النهج اسم تعلم التحويل للتعلم التقويمي (TRL).

الخاتمة

تعتبر تدرجات السياسة من بين أكثر الأساليب الأساسية لحل مشاكل التعلم التعزيزي.

 في هذه المقالة، قدمنا المبادئ الأساسية لتدرجات السياسة وأظهرنا كيفية اشتقاق نظرية تدرج السياسة. كما عرضنا كيفية تنفيذ خوارزمية بسيطة تعتمد على التدرج باستخدام PyTorch في بيئة Gymnasium. أخيرًا، ناقشنا التحديات العملية والإضافات الشائعة لخوارزمية تدرج السياسة الأساسية.

إذا كنت ترغب في تعميق فهمك للتعلم التعزيزي والتعلم العميق باستخدام PyTorch، تحقق من هذه الدورات:

• مسار التعلم التعزيزي – تعلم أساسيات التعلم التعزيزي، من الأساليب المعتمدة على القيمة إلى تقنيات تحسين السياسة.
• مقدمة في التعلم العميق باستخدام PyTorch – احصل على تجربة عملية مع PyTorch وابدأ في بناء نماذج التعلم العميق من الصفر.