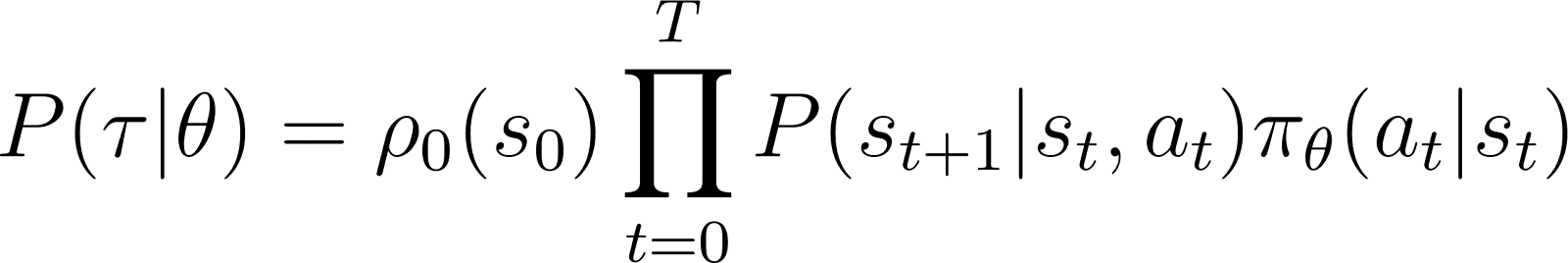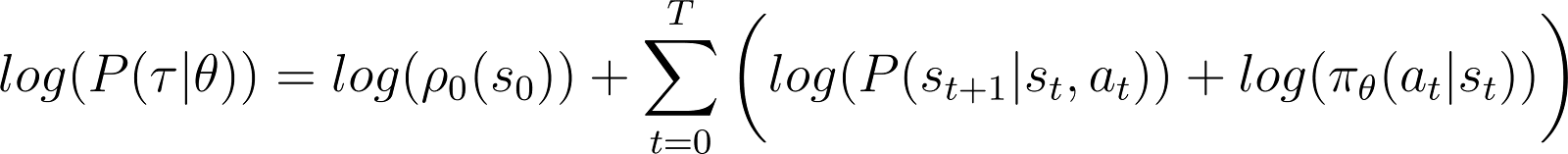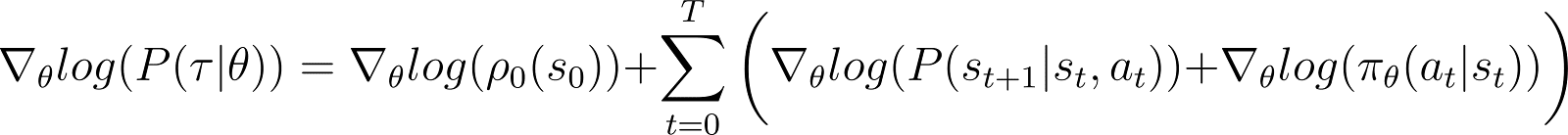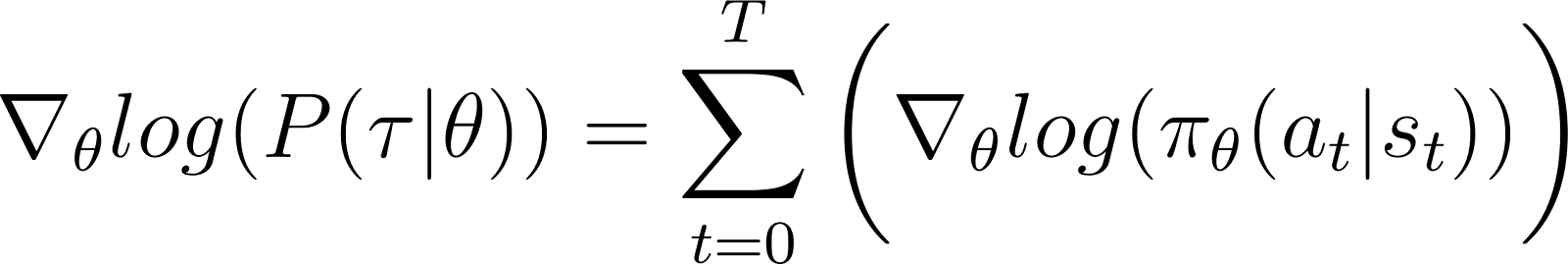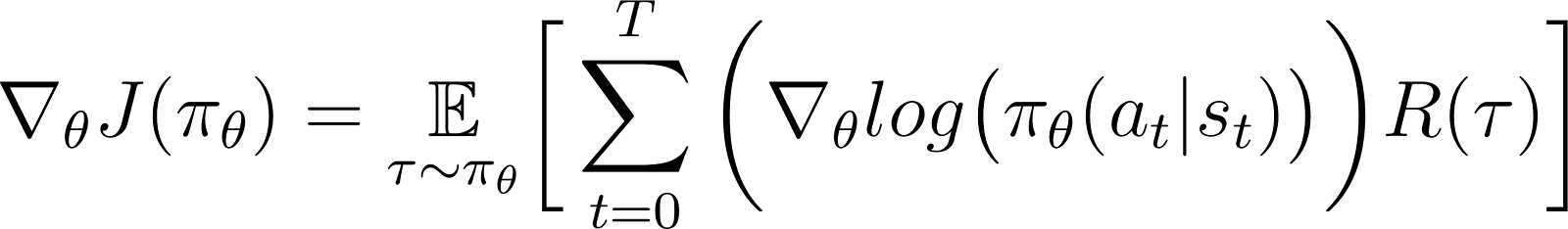Beleidshellingstelling Uitgelegd: Een Praktische Inleiding

Waarom beleidsgradentools gebruiken?

Een belangrijk voordeel van beleidsgradentools is hun vermogen om met complexe actieruimtes om te gaan, waar traditionele op waarde gebaseerde benaderingen moeite mee hebben.

Omgaan met hoog-dimensionale actieruimtes

Waarde-gebaseerde methoden, zoals Q-learning, werken door de waarde functie voor alle mogelijke acties te schatten. Dit wordt moeilijk wanneer de actie ruimte van de omgeving continu of discreet maar groot is.

Beleidsgraad methoden parametriseren het beleid en schatten de gradient van de cumulatieve beloningen ten opzichte van de beleidsparameters. Ze gebruiken deze gradient om het beleid rechtstreeks te optimaliseren door de parameters bij te werken. Daarom kunnen ze efficiënt omgaan met hoge-dimensionale of continue actie ruimtes. Beleidsgradiënten zijn ook de basis van Versterkend Leren met Menselijke Feedback (RLHF) methoden.

Door het beleid te parameteriseren en de parameters aan te passen op basis van gradiënten, kunnen beleidsgradiënten efficiënt omgaan met continue en hoge-dimensionale acties. Deze directe aanpak maakt betere generalisatie en flexibelere verkenning mogelijk, waardoor het goed geschikt is voor taken zoals robotcontrole en andere complexe omgevingen.

Leven van stochastische beleids

Gegeven een set observaties:

• Een deterministisch beleid specificeert welke actie de agent onderneemt.
• Een stochastisch beleid geeft een set acties en de waarschijnlijkheid dat de agent elke actie kiest.

Bij het volgen van een stochastisch beleid kan dezelfde observatie leiden tot het kiezen van verschillende acties in verschillende iteraties. Dit bevordert de verkenning van de actieruimte en voorkomt dat het beleid vastloopt in lokale optima. Om deze reden zijn stochastische beleidsvormen nuttig in omgevingen waar verkenning essentieel is om het pad te ontdekken dat leidt tot de maximale opbrengsten.

In beleid-gebaseerde methoden wordt de beleidsoutput omgezet in een waarschijnlijkheidsverdeling, waarbij elke mogelijke actie een waarschijnlijkheid toegewezen krijgt. De agent kiest een actie door deze verdeling te bemonsteren, waardoor het mogelijk wordt om een stochastisch beleid te implementeren. Zo combineren beleidgradiëntmethoden verkenning met exploitatie, wat nuttig is in omgevingen met complexe beloningsstructuren.

Afleiding van de Beleidsgradiëntstelling

Voordat we in de afleiding duiken, is het belangrijk om de wiskundige notatie en de belangrijkste concepten die in het bewijs worden gebruikt, vast te stellen.

Wiskundige notatie en preliminaires

Zoals vermeld in een vorige sectie, stelt de beleidsgraadstelling dat de afgeleide van de verwachte opbrengst de verwachting is van het product van de opbrengst en de afgeleide van de logaritme van het beleid.

Voordat we de beleidsgraadstelling afleiden, introduceren we de notatie:

• E[X] verwijst naar de probabilistische verwachting van een random variabele X.
• Wiskundig wordt het beleid uitgedrukt als een waarschijnlijkheidsmatrix die de kans geeft om verschillende acties te kiezen op basis van verschillende waarnemingen. Een beleid wordt meestal gemodelleerd als een geparametriseerde functie, waarbij de parameters worden weergegeven als θ.
• π_θ verwijst naar een beleid dat is geparametriseerd door θ. In de praktijk zijn deze parameters de gewichten van het neurale netwerk dat het beleid modelleert.
• De trajectorie, τ, verwijst naar een reeks van staten, meestal beginnend vanuit een willekeurige initiële staat tot aan ofwel de huidige tijdstap of de terminale staat.
• ∇_θf verwijst naar de gradient van een functie f ten opzichte van parameter(s) θ. 
• J(π_θ) verwijst naar het verwachte rendement dat door de agent wordt behaald volgens het beleid π_θ. Dit is ook de doelstelling voor gradient ascent.
• De omgeving geeft een beloning bij elke tijdstap, afhankelijk van de actie van de agent. De return verwijst naar de cumulatieve beloningen van de oorspronkelijke staat tot de huidige tijdstap.
• R(τ) verwijst naar het rendement gegenereerd over de trajectorie τ.

Ableidingstappen

We laten zien hoe we de beleidsgradiëntstelling kunnen afleiden en bewijzen vanuit eerste beginselen, beginnend met de uitbreiding van de doelfunctie en gebruikmakend van de log-afgeleide truc. 

De doelfunctie (Vergelijking 1)

De doelfunctie in de beleidsgradiëntmethode is de return.

Ik ben samengesteld door de trajecten te volgen op basis van het beleid π uitgedrukt in termen van parameters θ. Deze objectieve functie is als volgt:

In de bovenstaande vergelijking:

• De linkerkant (LHS) is het verwachte rendement dat wordt behaald door het volgen van het beleid π_θ.
• De rechterkant (RHS) is de verwachting (over de traject τ gegenereerd door het volgen van het beleid π_θ in elke stap) van de opbrengsten R(τ) gegenereerd over het traject τ.  

De differentiaal van de doelfunctie (Vergelijking 2)

Differentieren (met betrekking tot θ) beide zijden van de bovenstaande vergelijking geeft:

De gradient van de verwachting (Vergelijking 3)

De verwachting (aan de RHS) kan worden uitgedrukt als een integraal over het product van:

• De kans om een traject τ te volgen
• De rendementen gegenereerd over de trajectorie τ

Dus, de RHS van Vergelijking 2 wordt als volgt herhaald:

De gradiënt van een integraal is gelijk aan de integraal van de gradiënt. Dus, in de bovenstaande uitdrukking, kunnen we de gradiënt ∇_θ onder het integraalteken brengen. Dus, de RHS wordt:

Dus kan Vergelijking 2 worden herschreven als:

De kans op de trajectorie (Vergelijking 4)

We bekijken nu P(τ|θ), de kans dat de agent de traject volgt τ gegeven beleidsparameters θ (en dus beleid π_θ). Een traject bestaat uit een set stappen. Dus: 

• De kans om traject τ is het product van:
• De kans om alle individuele stappen te volgen.

• In de tijdstap t, gaat de agent van de staat s naar de staat s_t+1 door de actie a_t te volgen. De waarschijnlijkheid van dit gebeuren is het product van:
• De kans dat het beleid actie a_t in toestand s_t
• De waarschijnlijkheid om in staat te eindigen te zijns_t+1gegeven actiea_t en staats_t

Dus, uitgaande van een initiële toestand s₀, wordt de waarschijnlijkheid dat de agent traject τ volgt op basis van beleid π_θ als volgt gegeven: 

Om dingen eenvoudiger te maken, willen we het product aan de rechterkant hierboven uitdrukken als een som. Dus nemen we de logaritme aan beide zijden van de bovenstaande vergelijking:

De afgeleide van de log-kans (Vergelijking 5)

We nemen nu de afgeleide (ten opzichte van θ) van de log-kans in de bovenstaande vergelijking.

Aan de rechterkant van de bovenstaande vergelijking:

• De eerste term log ρ₀(s₀) is constant ten opzichte van θ. Dus is de afgeleide 0.
• De eerste term binnen de som P(s_t+1|s_t, a_t) is ook onafhankelijk van θ en de afgeleide ervan ten opzichte van θ is ook 0.

Door de bovengenoemde nultermen uit de vergelijking te verwijderen, blijven we over met (Vergelijking 5):

Vergeet niet uit Vergelijking 2 dat:

Vergelijking 5 evalueert de log van het eerste deel van de RHS van Vergelijking 2. We moeten de afgeleide van een term relateren aan zijn logaritme. Dit doen we met behulp van de kettingregel en de log-afgeleide truc.

De log-afgeleide truc

We nemen een omweg en gebruiken de regels van de calculus om een resultaat af te leiden, dat we zullen gebruiken om de vorige vergelijking te vereenvoudigen en geschikt te maken voor computermethoden.

In de calculus kan de afgeleide van een logaritme worden uitgedrukt als:

Door dus de bovenstaande vergelijking te herschikken, kan de afgeleide van x worden uitgedrukt in termen van de afgeleide van de logaritme van x:

Dit wordt soms de log-afgeleide truc genoemd.

De kettingregel

Volgens de kettingregel, gegeven z(y) als een functie van y, waar y zelf een functie is van θ, y(θ), de afgeleide van z met betrekking tot θ is gegeven als:

In dit geval, y(θ) staat voor P(θ) en z(y) staat voor log(y). Zo, 

Toepassen van de kettingregel

We weten uit de calculus dat d(log(y)) / dy = 1/y. Gebruik dit in de eerste uitdrukking van de RHS hierboven. 

Verplaats y naar de LHS en gebruik de notatie:

y staat voor P(θ). Dus de bovenstaande vergelijking is equivalent aan:

Toepassen van de logafgeleide truc

Het bovenstaande resultaat geeft de eerste uitdrukking van de RHS van Vergelijking 2 (hieronder weergegeven).

Door het resultaat in de RHS van Vergelijking 2 te gebruiken, krijgen we:

We herschikken de termen onder de RHS integraal als hieronder:

Afleiden van het eindresultaat

Merk op dat de bovenstaande uitdrukking de integrale uitbreiding van een verwachting bevat: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

Dus kan de RHS hierboven worden uitgedrukt als de verwachting:

We vervangen de afgeleide van de logwaarschijnlijkheid in de uitdrukking van de verwachte beloning:

In de bovenstaande vergelijking, vervang de waarde van ∇logP(θ) uit Vergelijking 5 om te krijgen:

Dit is de uitdrukking voor de gradiënt van de beloningsfunctie volgens de beleidsgradiëntstelling.

De intuïtie achter de beleidsgradiënt

Beleidsgradiëntmethoden zetten de uitvoer van het beleid om in een waarschijnlijkheidsverdeling. De agent monster deze verdeling om een actie te kiezen. Beleidsgradiëntmethoden passen de beleidsparameters aan. Dit leidt tot het bijwerken van deze waarschijnlijkheidsverdeling in elke iteratie. De bijgewerkte waarschijnlijkheidsverdeling heeft een grotere kans om acties te kiezen die leiden tot hogere beloningen.

Het beleidsgradiëntalgoritme berekent de gradiënt van het verwachte rendement ten opzichte van de beleidsparameters. Door de beleidsparameters in de richting van deze gradiënt te verplaatsen, vergroot de agent de kans om acties te kiezen die tijdens de training tot hogere beloningen leiden.

Wezenlijk worden acties die tot betere resultaten hebben geleid, geleidelijk waarschijnlijker gekozen in de toekomst, waarbij het beleid geleidelijk wordt verbeterd om langetermijnbeloningen te maximaliseren.

Het implementeren van Beleidsgradiënten in Python

Na de fundamentele principes van beleidsgradiënten te hebben besproken, laten we zien hoe we ze kunnen implementeren met behulp van PyTorch en Gymnasium.

Het opzetten van de omgeving

Als eerste stap moeten we gymnasium installeren en een paar ondersteunende bibliotheken zoals NumPy en PyTorch.

Om gymnasium en de bijbehorende afhankelijkheden op een server of lokale machine te installeren, voer je het volgende commando uit:

$ pip install gymnasium 

Om te installeren met behulp van een Notebook zoals Google Colab of DataLab, gebruik je:

!pip install gymnasium

Je importeert deze pakketten binnen de Python-omgeving:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

Het coderen van een eenvoudige beleidsgradiëntagent

Maak een instantie van de omgeving met behulp van de .make() methode.

env = gym.make('CartPole-v1')

Net als bij andere machine learning methoden, gebruiken we een neuraal netwerk om de policy gradient agent te implementeren.

CartPole-v1 is een eenvoudige omgeving, dus we ontwerpen een eenvoudig netwerk met 1 verborgen laag met 64 neuronen. De dimensie van de inputlaag is gelijk aan de dimensies van de observatieruimte. De dimensie van de outputlaag is gelijk aan de grootte van de actie ruimte van de omgeving. Zo mappt het policy netwerk waargenomen toestanden naar acties. Gegeven een observatie als input, geeft het netwerk de voorspelde actie terug volgens de policy.

De onderstaande code implementeert het policy netwerk:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

De agent trainen

De omgeving geeft een beloning in elke tijdstap afhankelijk van de staat en actie van de agent. De policy gradient benadering bestaat uit het uitvoeren van gradient descent op de cumulatieve beloningen (return). Het doel is om de totale return te maximaliseren.

Om de return in een episode te berekenen, accumuleer je (met een discontovoet) beloningen van alle tijdstappen in die episode. Bovendien is het normaliseren van de returns nuttig om een vloeiende en stabiele training te waarborgen. De onderstaande code laat zien hoe je dit doet:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

In elke iteratie van de forward pass doen we de volgende stappen:

• Voer de agent uit op basis van het huidige beleid met behulp van de .step() functie. Het beleid voorspelt de kans om de gekozen actie in elke tijdstap uit te voeren.
• Ontvang de beloning van de omgeving op basis van de actie van de agent.
• Accumuleer stapgewijze beloningen en de logkansen van de acties totdat de agent een terminale staat bereikt.

De onderstaande code implementeert de forward pass:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

Gebruik van backpropagation en gradient ascent om het beleid bij te werken

In traditionele machine learning:

• Verlies verwijst naar het verschil tussen de voorspelde en de werkelijke output.
• We minimaliseren het verlies met behulp van gradient descent.

In RL:

• Het verlies is een proxy voor de grootheid waarop gradiëntafstamming (of -stijging) moet worden toegepast. 
• We maximaliseren het rendement (cumulatieve beloningen) met behulp van gradiëntstijging.
• De verwachte waarde van het rendement wordt gebruikt als proxy voor het verlies voor gradiëntafstamming. De verwachte waarde van het rendement is het product van:
• De verwachte beloningen van elke stap met 
• De waarschijnlijkheid van het kiezen van de gesamplede actie in elke stap. 
• Om gradiëntstijging toe te passen met behulp van backpropagatie, gebruiken we het negatief van het verlies. 

De onderstaande code berekent het verlies:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

Vergelijkbaar met standaard machine learning algoritmen, om het beleid bij te werken, voer je backpropagatie uit ten opzichte van de verliesfunctie. De update_beleid() methode roept de bereken_verlies() methode aan. Vervolgens wordt backpropagatie uitgevoerd op dit verlies om de beleidsparameters bij te werken, d.w.z. modelgewichten van het beleidsnetwerk. 

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

De trainingslus

We gebruiken de eerder gedefinieerde functies om het beleid te trainen. Voordat we met de training beginnen, hebben we nodig: 

• Een ongeoefend beleid dat is geïnitialiseerd als een gerandomiseerde instantie van de PolicyNetwork-klasse. 
• Een optimizer die het Adam-algoritme gebruikt. 
• Hyperparameters voor de kortingen, leersnelheid, dropoutpercentage, beloningsdrempel en het maximale aantal trainingsepochen. 

We doorlopen de trainingslus totdat de gemiddelde terugkeer de beloningsdrempel overschrijdt. In elke iteratie voeren we de volgende stappen uit: 

• Voor elke aflevering, voer eenmaal de forward pass uit. Verzamel de logkans van acties, de stapgewijze rendementen en de totale terugkeer van die aflevering. Accumuleer de episodische rendementen in een array. 
• Bereken het verlies met behulp van de logkansen en de stapgewijze rendementen. Voer de backpropagation uit op het verlies. Gebruik de optimizer om de beleidsparameters bij te werken. 
• Controleer of de gemiddelde terugkeer over N_TRIALS de beloningsdrempel overschrijdt. 

De onderstaande code implementeert deze stappen:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

Voer het trainingsprogramma uit door de main() functie aan te roepen:

main()

Dit DataLab werkboek bevat de bovenstaande implementatie van het beleidsgraad algoritme. Je kunt het direct uitvoeren of het gebruiken als startpunt voor het aanpassen van het algoritme.

Voordelen en Uitdagingen van Beleidsgraadmethoden

Beleidsgraadmethoden bieden verschillende voordelen, zoals:

• Omgaan met continue actieruimten: Waarde-gebaseerde methoden (zoals Q-learning) zijn inefficiënt met continue actieruimten omdat ze waarden over de gehele actieruimte moeten schatten. Beleidsgraadmethoden kunnen het beleid direct optimaliseren met behulp van de gradient van de verwachte opbrengsten. Deze aanpak werkt goed met continue actieverdelingen. Daarom zijn beleidsgraadmethoden geschikt voor taken zoals robotbesturing die gebaseerd zijn op continue actieruimten.
• Stochastische beleids: Beleidsgraadmethoden kunnen stochastische beleids leren – die een kans geven om elke mogelijke actie te selecteren. Dit stelt de agent in staat om een verscheidenheid aan acties te proberen en vermindert het risico om vast te komen zitten in lokale optima. Het helpt in complexe omgevingen waar de agent de actieruimte moet verkennen om het optimale beleid te vinden. De stochastische aard helpt bij het balanceren van exploratie (nieuwe acties proberen) en exploitatie (de beste bekende acties kiezen), wat cruciaal is voor omgevingen met onzekerheid of schaarse beloningen.
• Directe beleidsoptimalisatie: Beleidsgradiënten optimaliseren het beleid direct in plaats van gebruik te maken van waarde-functies. In continue of hoog-dimensionale actie ruimtes kan het benaderen van waarden voor elke actie computationeel kostbaar worden. Daarom presteren op beleid gebaseerde methoden goed in dergelijke omgevingen.

Ondanks hun vele voordelen hebben beleidsgradiëntmethoden enkele inherente uitdagingen:

• Hoge variatie in gradient schattingen: Beleidsgraadmethoden selecteren acties door een kansverdeling te bemonsteren. In feite bemonsteren ze de trajecten om de verwachte opbrengst te schatten. Omdat het bemonsteringsproces inherent willekeurig is, kunnen de geschatte opbrengsten in latere iteraties een hoge variatie hebben. Dit kan het moeilijk maken voor de agent om efficiënt te leren, omdat de updates voor het beleid aanzienlijk kunnen fluctueren tussen iteraties. 
• Instabiliteit tijdens training: 
• Beleidsgraadmethoden zijn gevoelig voor hyperparameters zoals de. Als de leersnelheid te hoog is, kunnen de updates voor de beleidsparameters te groot zijn, waardoor de training de optimale parameters mist. Aan de andere kant, als de leersnelheid te laag is, kan de convergentie traag zijn. 
• Beleidsgraadmethoden moeten een balans vinden tussen verkenning en exploitatie. Als de agent niet genoeg verkent, kan hij de buurt van het optimale beleid niet bereiken. Omgekeerd, als hij te veel verkent, zal hij niet convergeren naar het optimale beleid en rond de actieruimte oscilleren.
• Monsterinefficiëntie: Beleidsgraadmethoden schatten de opbrengst door met elk beleid door te gaan tot beëindiging en de beloningen van elke stap te accumuleren. Daarom hebben ze veel interacties met de omgeving nodig om een groot aantal monstertrajecten te trekken. Dit is inefficiënt en kostbaar voor omgevingen met grote staat- of actieruimtes.

Oplossingen voor stabiliteit

Omdat instabiliteit een relatief veelvoorkomend probleem is bij beleidsgraadmethoden, hebben ontwikkelaars verschillende oplossingen aangenomen om het trainingsproces te stabiliseren. Hieronder introduceren we veelvoorkomende oplossingen voor het stabiliseren van de training met behulp van beleidsgraadmethoden:

Gebruik van basislijnfuncties

Door inefficiënte sampling kunnen de gradiënten van de rendementen die tijdens de trainingsiteraties zijn geschat, een hoge variantie hebben, waardoor de training instabiel en traag wordt. Een veelgebruikte aanpak om de variantie te verminderen, is het gebruik van baseline-functies, zoals de Advantage Actor-Critic (A2C) methode. Het idee is om een proxy (de voordeel-functie) te gebruiken in plaats van het geschatte rendement voor de doel functie.

Het voordeel wordt berekend als het verschil tussen het werkelijke rendement van de gesamplede traject en het verwachte rendement gezien de initiële staat. Deze aanpak houdt in dat de waarde functie wordt gebruikt als de verwachte waarde van staten en staat-actiepaar. Door het verlies weer te geven als het verschil tussen het werkelijke rendement en het verwachte rendement in plaats van alleen als de rendementen, vermindert A2C de variantie in de verliesfunctie en dus in de gradiënten, wat de training stabieler maakt.

Gebruik van entropie-regularisatie

In bepaalde omgevingen, zoals die met schaarse beloningen (slechts een paar staten geven een beloning), past het beleid snel een deterministische aanpak toe. Het neemt ook een hebzuchtige aanpak aan en benut de paden die al zijn verkend. Dit voorkomt verdere verkenning en leidt vaak tot convergentie naar lokale optima en suboptimale beleidslijnen.

De oplossing is om verkenning aan te moedigen door de beleidsmaatregel te straffen wanneer deze te deterministisch wordt. Dit wordt gedaan door een entropie-gebaseerde term toe te voegen aan de doelstelling. De entropie meet de hoeveelheid willekeurigheid in het beleid. Hoe groter de entropie, hoe meer willekeurigheid in de acties die door de agent worden gekozen. Deze entropie-gebaseerde term is het product van de entropiecoëfficiënt en de entropie van het huidige beleid.

Het opnemen van de entropie als onderdeel van de doelstelling helpt om een balans te bereiken tussen exploitatie en verkenning.

Beleidsgradientuitbreidingen

Onder de verschillende uitbreidingen van beleidsgradientmethoden is een van de meest fundamentele het REINFORCE-algoritme. Het biedt een rechttoe rechtaan implementatie van de beleidsgradientstelling en is de basis voor meer geavanceerde technieken.

REINFORCE-algoritme

Het REINFORCE-algoritme, ook wel bekend als Monte Carlo Reinforce, is een van de basisimplementaties van de policy gradient-theorema. Het maakt gebruik van Monte Carlo-methoden om opbrengsten en beleidsgradiënten te schatten. Bij het volgen van het REINFORCE-algoritme neemt de agent rechtstreeks alle acties (van de initiële tot de terminale staat) uit de omgeving. Dit staat in contrast met andere methoden zoals TD-Learning en Dynamische Programmatie, die hun acties baseren op schattingen van de waarde functie.

Hieronder presenteren we de basisstappen van het REINFORCE-algoritme:

• Initialiseer het beleid met willekeurige parameters
• Herhaal meerdere trainingsepisodes. Voor elke episode:
• Genereer elke stap van de gehele episode als volgt:
• Geef de staat door aan de beleidsfunctie.
• Het beleidsfunctie genereert waarschijnlijkheden voor elke mogelijke actie.
• Monster willekeurig een actie uit deze kansverdeling.
• Voor elke staat in de aflevering, schat de opbrengsten (verdisconteerde cumulatieve beloningen) tot stap.
• Schat de gradiënt van de doelfunctie (volgens de beleidsgradiënt stelling), uitgedrukt als het product van de stapsgewijze opbrengsten en de actiewaarschijnlijkheden voor elke stap.
• Werk de beleidsparameters bij door de gradiënten toe te passen

Voor elke beleid kun je een enkele traject monsteren om de gradiënt te schatten (zoals hierboven getoond) of de gradiënt gemiddeld over meerdere trajecten samplen onder hetzelfde beleid.

Actor-critic methoden

Actor-critic methoden combineren beleidsgradiëntmethoden (zoals REINFORCE) met waardefuncties.

• De werking van de actor is vergelijkbaar met beleidsgradiëntmethoden. De actor implementeert het beleid, selecteert acties in elke stap op basis van het beleid. Het update het beleid door de gradiënt van de verwachte return te volgen.
• De criticus implementeert de waardefunctie, die wordt gebruikt als een basislijn (besproken in de vorige sectie). Dit helpt om de training efficiënter en stabieler te maken.

Beleidsgradiëntmethoden zoals REINFORCE schatten de gradiënten langs elke trajectorie met behulp van de ruwe return. Omdat een bemonsteringsproces deze trajectorieën genereert, kan dit leiden tot grote variaties in de returns en gradiënten. Het gebruik van een voordeelfunctie in plaats van de ruwe returns lost dit probleem op. De voordeelfunctie is het verschil tussen de daadwerkelijke en verwachte returns (d.w.z. de waardefunctie). Acteur-criticusmethoden zijn een klasse van algoritmen. Wanneer de criticus wordt geïmplementeerd met behulp van de voordeelfunctie (de meest voorkomende benadering), wordt het ook wel Advantage actor-critic (A2C) genoemd.

Proximal Policy Optimization (PPO)

In complexe omgevingen zijn acteur-criticusmethoden zoals A2C alleen niet voldoende om de variatie in de returns en gradiënten onder controle te houden. In dergelijke gevallen kan het kunstmatig beperken van de mate waarin het beleid in elke iteratie kan veranderen helpen. Dit dwingt het bijgewerkte beleid (na gradiëntstijging) om in de buurt van het oude beleid te blijven.

Methoden zoals Proximal Policy Optimization maken twee aanpassingen aan beleidsgradiënten:

• Gebruik een voordeel functie. Typisch gebruikt deze voordeel functie de waarde functie als basislijn. In dit opzicht zijn ze vergelijkbaar met A2C-methoden. 
• Beperk de hoeveelheid waarmee de beleidsparameters in elke iteratie kunnen veranderen. Dit wordt gedaan met een geknipte surrogaatdoelfunctie. Het algoritme specificeert een bereik waarbinnen de verhouding van het nieuwe beleid tot het oude beleid moet liggen. Wanneer de verhouding (na de gradientupdate) deze vooraf bepaalde waarden overschrijdt, wordt deze geknipt zodat deze binnen het bereik blijft. 

Daarom verbetert PPO aanzienlijk de vanilla policy gradient methoden, wat de stabiliteit in complexe omgevingen bevordert. De geknipte doelfunctie voorkomt dat grote variaties in de rendementen en gradienten de beleidsupdates destabiliseren. Om een balans te bereiken tussen exploratie en exploitatie, is het ook mogelijk om PPO aan te passen om entropieregularisatie te gebruiken. Dit wordt gedaan door een entropieterm (een schaalparameter vermenigvuldigd met de entropie van het beleid) toe te voegen aan de doelfunctie.

Recente vooruitgangen

Policy gradients behoren tot de vroegste methoden die zijn gebruikt om RL-problemen op te lossen. Na de opkomst van snelle GPU’s zijn verschillende nieuwe benaderingen voorgesteld om moderne ML-technieken toe te passen op policy gradients.

Gradient-Boosterde Versterking Leerling

In de afgelopen jaren is er vooruitgang geboekt bij het toepassen van methoden zoals gradient boosting op RL-algoritmen. Gradient boosting combineert de voorspellingen van meerdere zwakke modellen om een enkel sterk model te genereren. Dit staat bekend als Gradient-Boosted Reinforcement Learning (GBRL). GBRL is een Python-pakket vergelijkbaar met XGBoost dat deze technieken implementeert voor RL-algoritmen.

Transfer Reinforcement Learning

Transfer learning (TL) is een techniek waarbij de kennis die is verkregen door één model wordt toegepast om de prestaties van een ander model te verbeteren. Transfer learning is nuttig omdat het trainen van ML-modellen vanaf nul duur is. TL-benaderingen zijn gebruikt in combinatie met beleidsgradiënten om de prestaties van RL-modellen te verbeteren. Deze benadering wordt ‘smeerd op Reinforcement Learning (TRL)’ genoemd.

Conclusie

Beleidsgradiënten behoren tot de meest fundamentele benaderingen om RL-problemen op te lossen.

 In dit artikel presenteerden we de eerste principes van beleidsgradiënten en toonden we hoe de beleidsgradiëntenstelling afgeleid kan worden. We lieten ook zien hoe je een eenvoudig op gradiënten gebaseerd algoritme kunt implementeren met behulp van PyTorch in een Gymnasium-omgeving. Ten slotte bespraken we praktische uitdagingen en veelvoorkomende uitbreidingen van het basisbeleidsgradiëntenalgoritme.

Als je je begrip van reinforcement learning en deep learning met PyTorch wilt verdiepen, bekijk dan deze cursussen:

• Reinforcement Learning Track – Leer de fundamenten van RL, van methoden gebaseerd op waarde tot beleidsoptimalisatietechnieken.
• Inleiding tot Deep Learning met PyTorch – Doe hands-on ervaring op met PyTorch en bouw deep learning modellen vanaf nul.