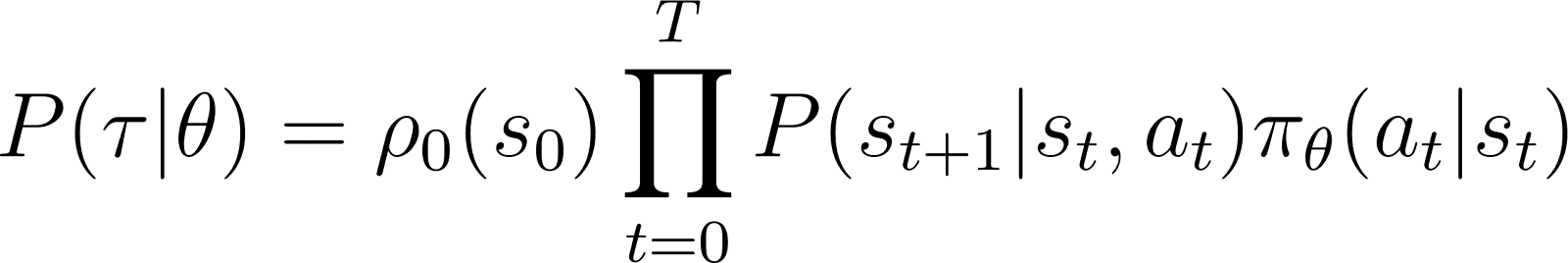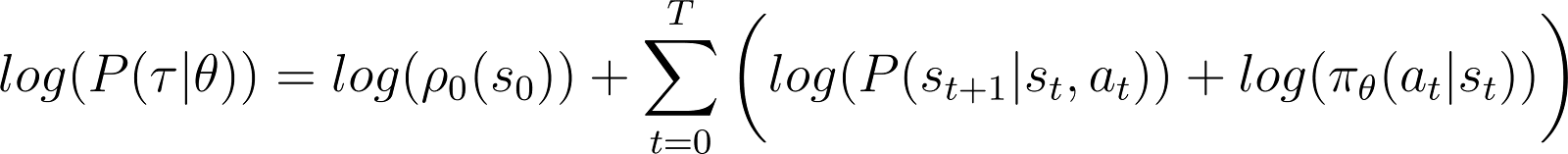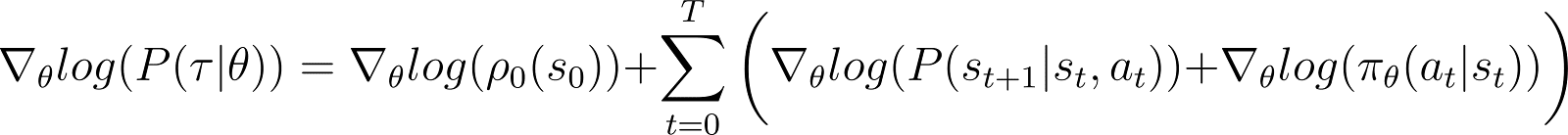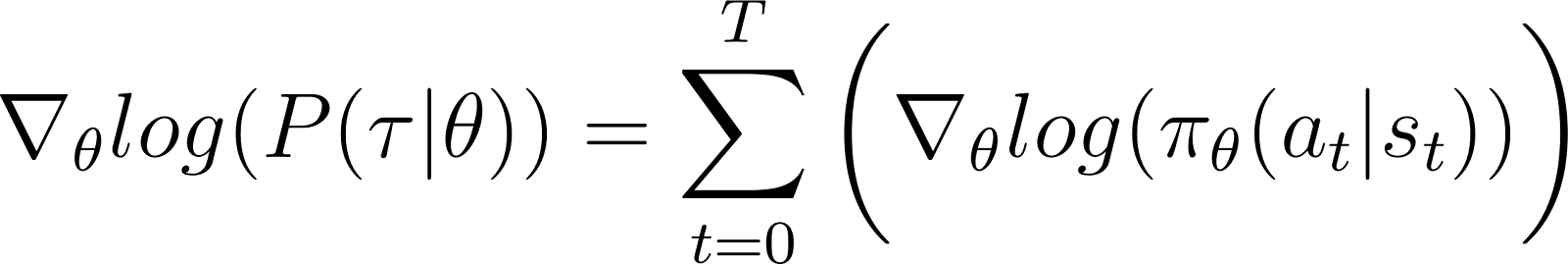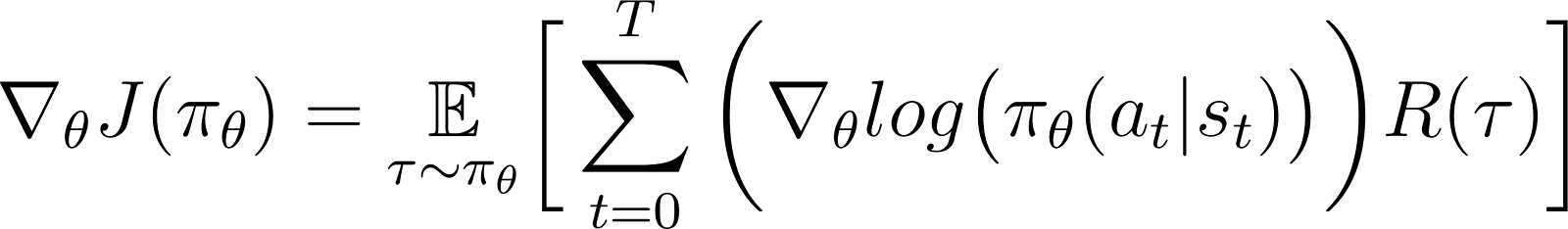Объяснение теоремы градиента политики: практическое введение

Почему использовать методы градиента политики?

Одно из ключевых преимуществ методов градиента политики заключается в их способности обрабатывать сложные пространства действий, где традиционные подходы на основе ценностей испытывают трудности.

Обработка пространств действий с высоким размером

Методы на основе оценки ценности, такие как Q-обучение, работают путем оценки функции ценности для всех возможных действий. Это становится сложным, когда пространство действий среды является непрерывным или дискретным, но большим.

Методы градиента политики параметризуют политику и оценивают градиент кумулятивных наград по отношению к параметрам политики. Они используют этот градиент для прямой оптимизации политики путем обновления ее параметров. Поэтому они могут эффективно обрабатывать пространства действий высокой размерности или непрерывные. Градиенты политики также являются основой методов Обучения с подкреплением с использованием обратной связи человека (RLHF).

Путем параметризации политики и корректировки ее параметров на основе градиентов градиенты политики могут эффективно обрабатывать непрерывные и высокоразмерные действия. Этот прямой подход обеспечивает лучшую обобщенность и более гибкое исследование, что делает его подходящим для задач, таких как управление роботами и другие сложные среды.

Обучение стохастических политик

Учитывая набор наблюдений:

• Детерминированная стратегия определяет, какое действие совершает агент.
• Стохастическая стратегия предоставляет набор действий и вероятность того, что агент выберет каждое действие.

При использовании стохастической стратегии одно и то же наблюдение может привести к выбору разных действий в разных итерациях. Это способствует исследованию пространства действий и предотвращает застревание стратегии в локальных оптимумах. Именно поэтому стохастические стратегии полезны в средах, где исследование является ключевым для обнаружения пути, ведущего к максимальным вознаграждениям.

В методах на основе стратегий вывод стратегии преобразуется в вероятностное распределение, при этом каждому возможному действию присваивается вероятность. Агент выбирает действие, выбирая образец из этого распределения, что позволяет реализовать стохастическую стратегию. Таким образом, методы градиента стратегии объединяют исследование с эксплуатацией, что полезно в средах с комплексными структурами вознаграждения.

Выведение Теоремы о Градиенте Стратегии

Перед тем как приступить к выводу, важно установить математическую нотацию и ключевые концепции, используемые во время доказательства.

Математическая нотация и предварительные сведения

Как упоминалось в предыдущем разделе, теорема о градиенте политики утверждает, что производная ожидаемого возврата является ожиданием произведения возврата и производной логарифма политики. 

Прежде чем получить теорему о градиенте политики, мы вводим нотацию:

• E[X] обозначает вероятностное ожидание случайной величины X. 
• С математической точки зрения, политика выражается в виде матрицы вероятностей, которая показывает вероятность выбора различных действий на основе различных наблюдений. Политика обычно моделируется как параметризованная функция, параметры которой представлены как θ.
• π_θ относится к политике, параметризованной θ. На практике эти параметры представляют собой веса нейронной сети, моделирующей политику. 
• Траектория, τ, обозначает последовательность состояний, обычно начиная с случайного начального состояния до текущего временного шага или конечного состояния.
• ∇_θf относится к градиенту функции f относительно параметра(ов) θ. 
• J(π_θ) относится к ожидаемому доходу, достигаемому агентом, следуя политике π_θ. Это также целевая функция для градиентного восхождения.
• Среда дает вознаграждение на каждом временном шаге в зависимости от действия агента. Возврат относится к накопленным вознаграждениям от начального состояния до текущего временного шага.
• R(τ) относится к доходности, генерируемой по траектории τ.

Шаги вывода

Мы покажем, как получить и доказать теорему о градиенте политики с первых принципов, начиная с разложения целевой функции и используя трюк с логарифмической производной.

Целевая функция (Уравнение 1)

Целевая функция в методе градиента политики – это возврат.

J накопленный в результате следования траектории, основанной на политике π , выраженной через параметры θ. Эта целевая функция задается как:

В приведенном уравнении: 

• Левая сторона (LHS) представляет собой ожидаемую доходность, достигнутую при следовании политике π_θ.
• Правая сторона (RHS) является ожиданием (по траектории τ , генерируемой следованием политики π_θ на каждом шаге) возвратов R(τ), генерируемых по траектории τ.   

Дифференциал целевой функции (Уравнение 2)

Дифференцируя (по отношению к θ) обе стороны указанного уравнения, получаем:

Градиент ожидания (Уравнение 3)

Ожидание (на ППП) можно выразить как интеграл от произведения:

• Вероятность следования траектории τ
• Возвраты, генерируемые на траектории τ

Таким образом, правая часть уравнения 2 переформулирована как:

Градиент интеграла равен интегралу градиента. Таким образом, в выражении выше мы можем перенести градиент ∇_θ под знаком интеграла. Таким образом, ППП становится: 

Таким образом, уравнение 2 можно переписать как:

Вероятность траектории (уравнение 4)

Мы теперь внимательно рассмотрим P(τ|θ), вероятность агента следовать траектории τ при заданных параметрах политики θ (и, следовательно, политика π_θ). Траектория состоит из набора шагов. Таким образом:

• Вероятность получения траектории τ является произведением:
• Вероятность выполнения всех отдельных шагов.

• На временном шаге t, агент переходит из состояния s в состояние s_t+1 , следуя действию a_t. Вероятность этого события равна произведению:
• Вероятность того, что политика предсказывает действие a_t в состоянии s_t
• Вероятность оказаться в состоянии s_t+1 при выполнении действия a_t и состоянии s_t

Таким образом, начиная с начального состояния s₀, вероятность того, что агент будет следовать траектории τ на основе политики π_θ задается как:

Чтобы упростить задачу, мы хотим выразить произведение в правой части уравнения выше в виде суммы. Поэтому мы берем логарифм с обеих сторон вышеуказанного уравнения:

Производная логарифмической вероятности (Уравнение 5)

Теперь мы берем производную (по θ) логарифмической вероятности в вышеприведенном уравнении.

С правой стороны вышеуказанного уравнения:

• Первый член log ρ₀(s₀) является постоянной по отношению к θ. Поэтому его производная равна 0.
• Первый термин внутри суммы P(s_t+1|s_t, a_t) также не зависит от θ и его производной по отношению к θ также равна 0. 

Удаление нулевых членов из уравнения приводит к (Уравнение 5):

Помним из Уравнения 2, что:

Уравнение 5 оценивает логарифм первой части правой части Уравнения 2. Нам нужно связать производную члена с его логарифмом. Мы делаем это, используя правило цепочки и трюк с логарифмической производной.

Трюк с логарифмической производной

Мы делаем обход и используем правила исчисления для вывода результата, который мы будем использовать для упрощения предыдущего уравнения и приведения его в удобную для вычислений форму.

В исчислении производная логарифма может быть выражена как:

Таким образом, переставив вышеуказанное уравнение, производная x может быть выражена через производную логарифма x:

Это иногда называется логарифмическим трюком производной.

Правило цепочки

Согласно правилу цепочки, учитывая z(y) как функцию y, где y сам по себе является функцией θ, y(θ), производная z по отношению к θ задаётся следующим образом:

В этом случае, y(θ) обозначает P(θ) и z(y) обозначает log(y). Таким образом,

Применение правила цепочки

Мы знаем из математического анализа, что d(log(y)) / dy = 1/y. Используйте это в первом выражении в RHS выше.

Перенесите y в LHS и используйте обозначение:

y обозначает P(θ). Таким образом, вышеуказанное уравнение эквивалентно:

Применение трюка с логарифмической производной

Вышеприведенный результат дает первое выражение в правой части уравнения 2 (показанное ниже).

Используя результат в правой части уравнения 2, мы получаем:

Мы перегруппируем члены под интегралом в правой части уравнения:

Получение окончательного результата

Обратите внимание, что вышеупомянутое выражение содержит интегральное разложение ожидания: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

Таким образом, правая часть выше может быть выражена как ожидание:

Мы подставляем производную логарифмической вероятности в выражение ожидаемой награды:

В указанном уравнении подставьте значение ∇logP(θ) из Уравнения 5, чтобы получить:

Это выражение для градиента функции вознаграждения в соответствии с теоремой градиента политики.

Интуиция за градиентом политики

Методы градиента политики преобразуют выходные данные политики в распределение вероятностей. Агент выбирает действие, основываясь на этой выборке. Методы градиента политики настраивают параметры политики. Это приводит к обновлению этого распределения вероятностей на каждой итерации. Обновленное распределение вероятностей имеет более высокую вероятность выбора действий, которые приводят к более высоким вознаграждениям. 

Алгоритм градиента политики вычисляет градиент ожидаемого дохода относительно параметров политики. Перемещая параметры политики в направлении этого градиента, агент увеличивает вероятность выбора действий, которые приводят к более высоким вознаграждениям в процессе обучения.

По сути, действия, которые привели к лучшим результатам, становятся более вероятными для выбора в будущем, постепенно улучшая политику для максимизации долгосрочных вознаграждений.

Реализация градиентов политики на Python

Обсудив основные принципы градиентов политики, мы покажем, как их реализовать с использованием PyTorch и Gymnasium.

Настройка окружения

В качестве первого шага нам нужно установить gymnasium и несколько поддерживающих библиотек, таких как NumPy и PyTorch.

Чтобы установить gymnasium и его зависимости на сервере или локальной машине, выполните:

$ pip install gymnasium 

Чтобы установить с использованием Ноутбука, такого как Google Colab или DataLab, используйте:

!pip install gymnasium

Вы импортируете эти пакеты в среде Python:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

Кодирование простого агента градиента политики

Создайте экземпляр окружения, используя метод .make().

env = gym.make('CartPole-v1')

Как и в других методах машинного обучения, мы используем нейронную сеть для реализации агента градиента политики.

CartPole-v1 — это простое окружение, поэтому мы проектируем простую сеть с одним скрытым слоем из 64 нейронов. Размер входного слоя равен размерам пространства наблюдений. Размер выходного слоя равен размеру пространства действий окружения. Таким образом, политика сети сопоставляет наблюдаемые состояния с действиями. Учитывая наблюдение в качестве входных данных, сеть выдает предсказанное действие в соответствии с политикой.

Код ниже реализует политику сети:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

Обучение агента

Окружение выдает награду на каждом временном шаге в зависимости от состояния и действия агента. Подход градиента политики состоит в том, чтобы выполнять градиентный спуск по накопленным наградам (возврату). Цель состоит в том, чтобы максимизировать общий возврат.

Чтобы рассчитать возврат в эпизоде, вы накапливаете (с учетом коэффициента дисконтирования) награды за все временные шаги в этом эпизоде. Кроме того, нормализация возвратов полезна для обеспечения плавного и стабильного обучения. Код ниже показывает, как это сделать:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

В каждой итерации прямого прохода мы выполняем следующие шаги:

• Запускаем агента на основе текущей политики, используя функцию .step(). Политика предсказывает вероятность выбора определенного действия на каждом временном шаге.
• Получаем вознаграждение от среды на основе действий агента.
• Накапливаем пошаговые вознаграждения и логарифмы вероятностей действий до тех пор, пока агент не достигнет терминального состояния.

Приведенный ниже код реализует прямой проход:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

Используем обратное распространение и градиентный подъем для обновления политики

В традиционном машинном обучении:

• Потеря относится к разнице между предсказанным и фактическим результатом.
• Мы минимизируем потери с помощью градиентного спуска.

В RL:

• Потеря является прокси-переменной, на которую должен быть применен градиентный спуск (или подъем). 
• Мы максимизируем возврат (накопленные награды), используя градиентный подъем.
• Ожидаемое значение возврата используется в качестве прокси-переменной для потерь при градиентном спуске. Ожидаемое значение возврата является произведением:
• Возвратов, ожидаемых на каждом шаге с 
• Вероятностью выбора выбранного действия на каждом шаге. 
• Для применения градиентного подъема с использованием обратного распространения, мы используем отрицание потерь. 

Приведенный ниже код рассчитывает потери:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

Аналогично стандартным алгоритмам машинного обучения, для обновления политики необходимо выполнить обратное распространение относительно функции потерь. Метод update_policy() ниже вызывает метод calculate_loss(). Затем выполняется обратное распространение по этим потерям для обновления параметров политики, то есть модельных весов сети политики. 

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

Цикл обучения

Мы используем ранее определенные функции для обучения политики. Перед началом обучения нам необходимо:

• Нетренированная политика, инициализированная как случайный экземпляр класса PolicyNetwork.
• Оптимизатор, использующий алгоритм Adam.
• Гиперпараметры для коэффициента дисконтирования, скорости обучения, коэффициента отсева, порога вознаграждения и максимального количества эпох обучения.

Мы повторяем цикл обучения до тех пор, пока среднее вознаграждение не превысит порог. На каждой итерации мы выполняем следующие шаги:

• Для каждого эпизода выполняем прямой проход один раз. Собираем логарифм вероятности действий, пошаговые вознаграждения и общее вознаграждение из этого эпизода. Накапливаем эпизодические вознаграждения в массиве.
• Рассчитываем потери, используя логарифмы вероятностей и пошаговые вознаграждения. Запускаем обратное распространение ошибки на потерях. Используем оптимизатор для обновления параметров политики.
• Проверяем, превышает ли среднее вознаграждение за N_TRIALS порог вознаграждения.

Приведенный ниже код реализует эти шаги:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

Запустите тренировочную программу, вызвав функцию main():

main()

Этот блокнот DataLab содержит вышеуказанную реализацию алгоритма градиента политики. Вы можете запустить его напрямую или использовать в качестве отправной точки для модификации алгоритма.

Преимущества и проблемы методов градиента политики

Методы градиента политики предлагают несколько преимуществ, таких как:

• Обработка непрерывных пространств действий: Методы, основанные на значениях (например, Q-обучение), неэффективны с непрерывными пространствами действий, поскольку им требуется оценка значений по всему пространству действий. Методы градиента политики могут напрямую оптимизировать политику, используя градиент ожидаемых вознаграждений. Этот подход хорошо работает с непрерывными распределениями действий. Таким образом, методы градиента политики подходят для задач, таких как робототехническое управление, основанное на непрерывных пространствах действий.
• Стохастические политики: Методы градиента политики могут обучаться стохастическим политикам – которые предоставляют вероятность выбора каждого возможного действия. Это позволяет агенту попробовать разнообразные действия и снизить риск застрять в локальных оптимумах. Это помогает в сложных средах, где агенту необходимо исследовать пространство действий, чтобы найти оптимальную политику. Стохастический характер помогает балансировать исследование (попытки новых действий) и эксплуатацию (выбор лучше всего известных действий), что крайне важно для сред с неопределенностью или разреженными вознаграждениями.
• Прямая оптимизация политики: Градиенты политики оптимизируют политику напрямую, а не используют функции ценности. В непрерывных или высокоразмерных пространствах действий аппроксимация значений для каждого действия может стать вычислительно дорогостоящей. Таким образом, методы, основанные на политике, хорошо себя проявляют в таких средах.

Несмотря на их многочисленные преимущества, методы градиента политики имеют некоторые врожденные проблемы:

• Высокая дисперсия в оценках градиента: Методы градиента политики выбирают действия,sampling a probability distribution. По сути, они отбирают траекторию для оценки ожидаемой прибыли. Поскольку процесс выборки по своей природе случайный, оцененные прибыли в последующих итерациях могут иметь высокую дисперсию. Это может затруднить агенту эффективное обучение, поскольку обновления политики могут значительно колебаться между итерациями.
• Нестабильность во время обучения:
• Методы градиента политики чувствительны к гиперпараметрам, таким как скорость обучения. Если скорость обучения слишком высока, обновления параметров политики могут быть слишком большими, что приводит к тому, что обучение пропускает оптимальные параметры. С другой стороны, если скорость обучения слишком мала, сходимость может быть медленной.
• Методы градиента политики должны балансировать между исследованием и эксплуатацией. Если агент не исследует достаточно, он может не достичь окрестностей оптимальной политики. Напротив, если он исследует слишком много, он не будет сходиться к оптимальной политике и будет колебаться вокруг пространства действий.
• Неэффективность выборки: Методы градиента политики оценивают возврат, следуя по каждой политике до завершения и накапливая награды с каждого шага. Таким образом, им требуется много взаимодействий с окружением, чтобы получить большое количество выборок траекторий. Это неэффективно и дорого для окружений с большими пространствами состояний или действий.

Решения для стабильности

Поскольку нестабильность является относительно распространенной проблемой в методах градиента политики, разработчики приняли различные решения для стабилизации процесса обучения. Ниже мы представляем общие решения для стабилизации обучения с использованием градиентов политики:

Использование базовых функций

Из-за неэффективной выборки градиенты доходов, оцененные в ходе итераций обучения, могут иметь высокую дисперсию, что делает обучение нестабильным и медленным. Распространенный подход к снижению дисперсии заключается в использовании базовых функций, таких как метод Advantage Actor-Critic (A2C). Идея состоит в том, чтобы использовать прокси (функцию преимущества) вместо оцененного дохода для целевой функции.

Преимущество рассчитывается как разница между фактическим доходом от sampled траектории и ожидаемым доходом, учитывая начальное состояние. Этот подход включает использование функции ценности в качестве ожидаемого значения состояний и пар состояние-действие. Представляя потери как разницу между фактическим доходом и ожидаемым доходом, а не только как доходы, A2C уменьшает дисперсию в функции потерь и, следовательно, в градиентах, делая обучение более стабильным.

Использование регуляризации энтропии

В некоторых средах, таких как те, в которых редкие вознаграждения (только очень немногие состояния дают вознаграждение), политика быстро принимает детерминированный подход. Она также принимает жадный подход и использует пути, которые уже были исследованы. Это препятствует дальнейшему исследованию и часто приводит к сходимости к локальным оптимумам и субоптимальным политикам.

Решение заключается в поощрении исследований по установлению штрафов за политику, когда она становится слишком детерминированной. Это достигается добавлением термина, основанного на энтропии, к целевой функции. Энтропия измеряет количество случайности в политике. Чем больше энтропия, тем больше случайности в действиях, выбранных агентом. Этот термин, основанный на энтропии, является произведением коэффициента энтропии и энтропии текущей политики.

Включение энтропии в целевую функцию помогает достичь баланса между эксплуатацией и исследованием.

Расширения политики градиентов

Среди различных расширений методов градиента политики одним из самых фундаментальных является алгоритм REINFORCE. Он обеспечивает простую реализацию теоремы о градиенте политики и является основой для более продвинутых техник.

Алгоритм REINFORCE

Алгоритм REINFORCE, также известный как Монте-Карло REINFORCE, является одной из основных реализаций теоремы градиента политики. Он использует методы Монте-Карло для оценки доходов и градиентов политики. При следовании алгоритму REINFORCE агент непосредственно выбирает все действия (от начального до конечного состояния) из среды. Это контрастирует с другими методами, такими как TD-обучение и динамическое программирование, которые используют бутстреп для своих действий на основе оценок функции ценности.

Ниже представлены основные шаги алгоритма REINFORCE:

• Инициализируйте политику случайными параметрами
• Повторяйте несколько тренировочных эпизодов. Для каждого эпизода:
• Сгенерируйте каждый шаг всего эпизода следующим образом:
• Передайте состояние функции политики.
• Функция политики генерирует вероятности для каждого возможного действия.
• Случайным образом выберите действие из этого распределения вероятностей.
• Для каждого состояния в эпизоде оцените возвраты (дисконтированные накопленные награды) до шага.
• Оцените градиент целевой функции (согласно теореме о градиенте политики), выраженный как произведение пошаговых возвратов и вероятностей действий для каждого шага.
• Обновите параметры политики, применяя градиенты.

Для каждой политики вы можете взять одну траекторию для оценки градиента (как показано выше) или усреднить градиент по нескольким траекториям, взятым по одной и той же политике.

Методы актёр-критик

Методы актёр-критик комбинируют методы градиента политики (например, REINFORCE) с функциями ценности.

• Работа актёра аналогична методам градиента политики. Актёр реализует политику, выбирая действия на каждом шаге на основе политики. Он обновляет политику, следуя градиенту ожидаемого вознаграждения.
• Критик реализует функцию ценности, которая используется в качестве базовой (обсуждалось в предыдущем разделе). Это помогает сделать обучение более эффективным и стабильным.

Методы политики градиента, такие как REINFORCE, оценивают градиенты вдоль каждой траектории, используя исходный возврат. Поскольку процесс выборки рисует эти траектории, это может привести к большим дисперсиям в возвратах и градиентах. Использование функции преимущества вместо исходных возвратов решает эту проблему. Функция преимущества представляет собой разницу между фактическими и ожидаемыми возвратами (т.е. функцией значения). Методы актер-критик – это класс алгоритмов. Когда критик реализован с использованием функции преимущества (самый распространенный подход), его также называют Актер-критик с преимуществом (A2C).

Проксимальная оптимизация политики (PPO)

В сложных средах методы актер-критик, подобные A2C, в одиночку недостаточно для контроля дисперсии в возвратах и градиентах. В таких случаях искусственное ограничение количества, на которое политика может измениться в каждой итерации, помогает. Это заставляет обновленную (после градиентного восхождения) политику находиться в окрестности старой политики.

Методы, подобные Проксимальной оптимизации политики, вносят две модификации в политику градиентов:

• Используйте функцию преимущества. Обычно эта функция преимущества использует функцию значения в качестве базовой. В этом они похожи на методы A2C. 
• Ограничьте величину, на которую параметры политики могут изменяться в каждой итерации. Это делается с использованием обрезанной заменяющей целевой функции. Алгоритм задает диапазон, в котором соотношение новой политики к старой политике должно находиться. Когда это соотношение (после обновления градиента) превышает заранее определенные значения, оно обрезается, чтобы оставаться в пределах диапазона. 

Таким образом, PPO значительно улучшает методы градиента политик, что повышает стабильность в сложных средах. Обрезанная целевая функция предотвращает большие вариации в доходах и градиентах от дестабилизации обновлений политики. Для достижения баланса между исследованием и эксплуатацией также можно модифицировать PPO для использования регуляризации энтропии. Это достигается добавлением термина энтропии (коэффициент масштабирования, умноженный на энтропию политики) к целевой функции.

Недавние достижения

Градиенты политики являются одними из первых методов, использованных для решения задач RL. После появления быстрых графических процессоров были предложены различные новые подходы для применения современных методов машинного обучения к градиентам политики.

Градиентно-усиленное обучение с подкреплением

В последние годы были сделаны успехи в применении методов, таких как градиентный бустинг, к алгоритмам RL. Градиентный бустинг объединяет прогнозы нескольких слабых моделей, чтобы создать одну сильную модель. Это называется Градиентно-усиленное обучение (GBRL). GBRL – это пакет на Python, подобный XGBoost, который реализует эти техники для алгоритмов RL.

Перенос обучения с подкреплением

Перенос обучения (TL) – это техника, при которой знания, полученные одной моделью, применяются для улучшения работы другой модели. Перенос обучения полезен, потому что обучение моделей ML с нуля дорого. TL подходы были использованы с градиентами политики для улучшения работы моделей RL. Этот подход называется Перенос обучения с подкреплением (TRL).

Заключение

Градиенты политики являются одним из самых основных подходов к решению задач RL.

В этой статье мы представили основные принципы градиентов политики и показали, как вывести теорему градиента политики. Мы также продемонстрировали, как реализовать простой алгоритм на основе градиента с использованием PyTorch в среде Gymnasium. Наконец, мы обсудили практические проблемы и общие расширения базового алгоритма градиента политики.

Если вы хотите углубить свои знания в области обучения с подкреплением и глубокого обучения с PyTorch, ознакомьтесь с этими курсами:

• Курс по обучению с подкреплением – Изучите основы RL, от методов на основе ценностей до техник оптимизации политики.
• Введение в глубокое обучение с PyTorch – Получите практический опыт работы с PyTorch и создайте модели глубокого обучения с нуля.