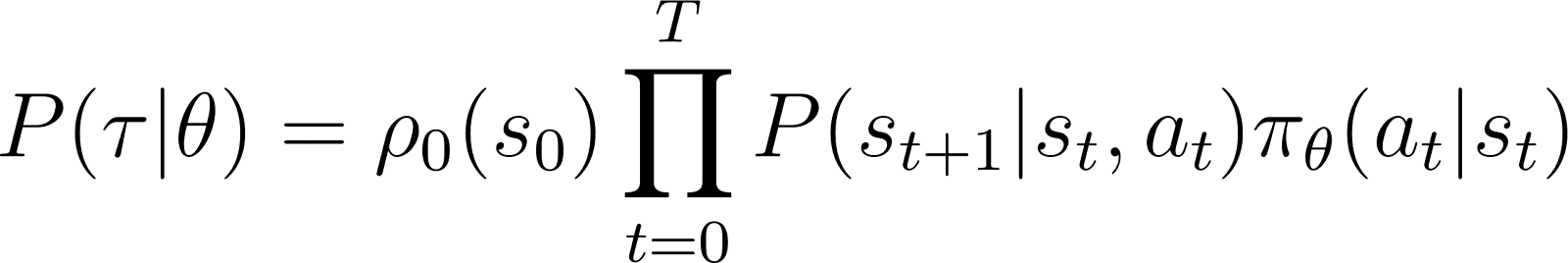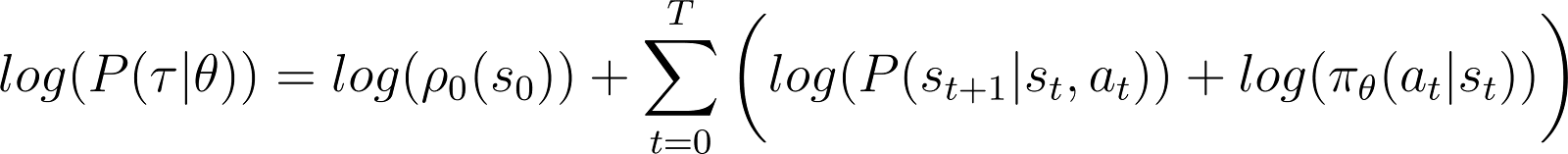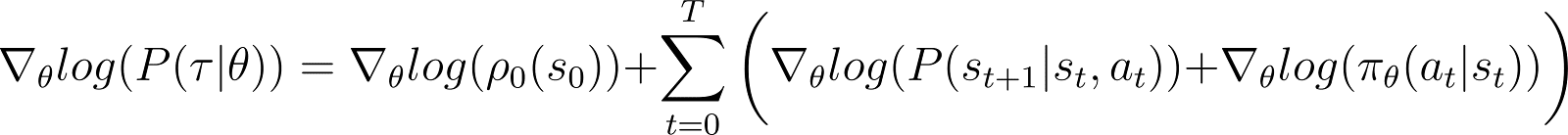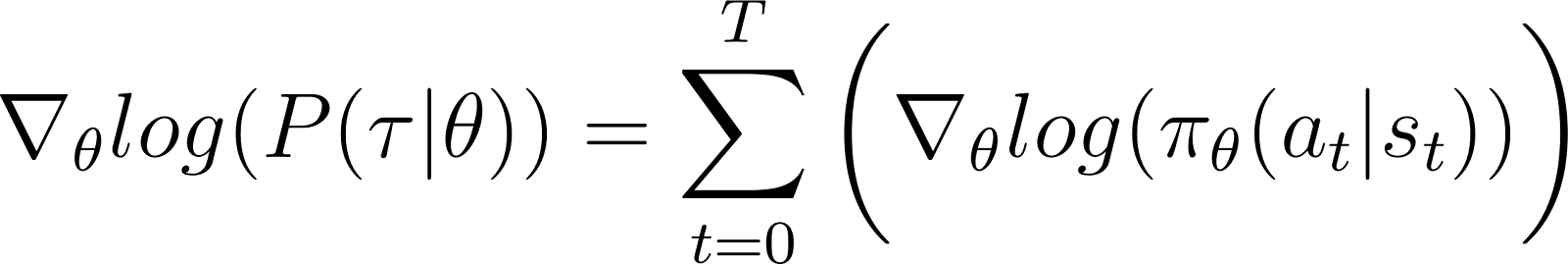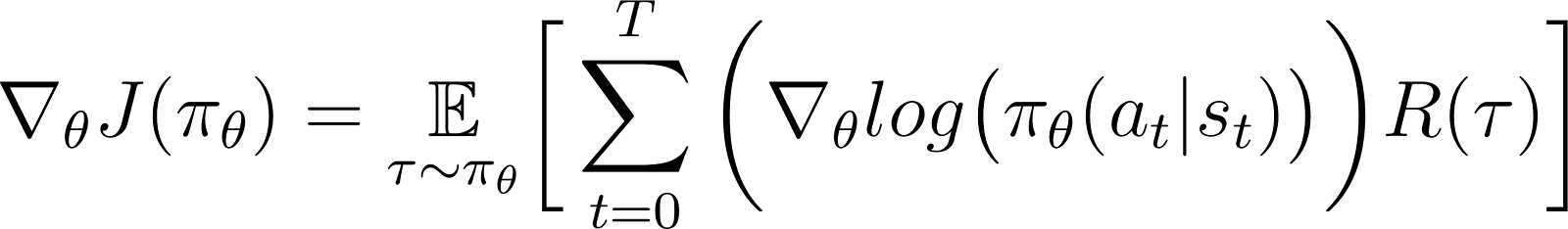策略梯度定理解释：实战导论

为什么使用策略梯度方法？

策略梯度方法的一个关键优势是其能够处理复杂的动作空间，传统价值方法难以应对。

处理高维度的动作空间

基于价值的方法，例如Q学习，通过估计所有可能行动的价值函数来工作。当环境的行动空间是连续的或离散但又很大时，这变得困难。

策略梯度方法对策略进行参数化，并估计与策略参数相关的累积奖励的梯度。它们使用这个梯度直接优化策略，通过更新其参数。因此，它们能够有效处理高维或连续的行动空间。策略梯度也是使用人类反馈的强化学习（RLHF）方法的基础。

通过对策略进行参数化并根据梯度调整其参数，策略梯度能够有效处理连续和高维的行动。这种直接的方法使得更好的泛化和更灵活的探索成为可能，特别适合于机器人控制和其他复杂环境等任务。

学习随机策略

给定一组观察：

• 确定性策略指定了代理程序采取的行动。
• 随机策略给出一组行动以及代理程序选择每个行动的概率。

遵循随机策略时，相同的观察结果可能导致在不同迭代中选择不同的行动。这有助于探索行动空间，并防止策略陷入局部最优解。因此，随机策略在需要探索以发现通往最大回报路径的环境中很有用。

在基于策略的方法中，策略输出被转换为概率分布，每个可能的行动被分配一个概率。代理程序通过对该分布进行抽样来选择行动，从而实现了随机策略。因此，策略梯度方法将探索与利用结合起来，适用于具有复杂奖励结构的环境。

策略梯度定理的推导

在深入推导之前，建立数学符号和整个证明过程中使用的关键概念是非常重要的。

数学符号和预备知识

正如前面的部分所述，策略梯度定理指出预期回报的导数是回报与策略对数的导数的乘积的期望值。

在推导策略梯度定理之前，我们引入以下符号：

• E[X]表示随机变量X的概率期望。
• 在数学上，策略被表示为一个概率矩阵，基于不同的观察结果给出选择不同动作的概率。策略通常被建模为一个参数化函数，其中参数表示为θ。
• π_θ 指的是由θ参数化的策略。在实践中，这些参数是模拟策略的神经网络的权重。
• 轨迹，τ，指的是一系列状态，通常从随机的初始状态开始，直到当前时间步或终止状态。
• ∇_θf 指的是函数 f 相对于参数 θ 的梯度。
• J(π_θ) 指的是代理根据策略 π_θ 所实现的预期回报。这也是梯度上升的目标函数。
• 环境根据代理的行动在每个时间步提供奖励。回报是指从初始状态到当前时间步的累积奖励。
• R(τ)指的是在轨迹τ上产生的回报。

推导步骤

我们展示如何从第一原理推导和证明策略梯度定理，从目标函数的展开开始，使用对数导数技巧。

目标函数（方程1）

策略梯度方法中的目标函数是回报

J根据基于政策π 表达的参数θ的轨迹累积。该目标函数如下：

在上述方程中：

• 左侧（LHS）是通过遵循策略π_θ实现的预期回报。
• 右侧 (RHS) 是在每一步遵循策略 π_θ 生成的轨迹 τ 上的回报 R(τ) 的期望τ。

目标函数的微分（方程2）

对上述方程两边分别进行微分（相对于θ）得到：

期望的梯度（方程3）

右侧的期望可以表示为乘积的积分：

• 遵循轨迹的概率 τ
• 在轨迹上产生的回报 τ

因此，方程2的右侧可以重新表述为：

积分的梯度等于梯度的积分。因此，在上述表达式中，我们可以将梯度 ∇_θ 移至积分符号下方。因此，右侧变为：

因此，方程2可以改写为：

轨迹的概率（方程4）

我们现在更仔细地看一下 P(τ|θ)，即代理根据轨迹 τ 遵循策略参数 θ (因此遵循策略 π_θ)。一个轨迹包括一系列步骤。因此：

• 获得轨迹τ 的概率是以下因子的乘积：
• 遵循所有个别步骤的概率。

• 在时间步t中，代理从状态s转移到状态s_t+1，遵循动作a_t的概率是以下乘积：
• 该政策预测在状态a_t中采取行动的概率 s_t
• 在给定动作a_t和状态s_t的情况下，最终处于状态s_t+1

因此，从初始状态 s₀开始，智能体遵循基于策略 π_θτ的轨迹的概率为：

为了简化问题，我们希望将上面的RHS产品表示为一个和。因此，我们对上述方程两边取对数：

对数概率的导数（方程5）

现在我们对上述方程中的对数概率进行导数（相对于θ）。

在上述方程的RHS：

• 第一项 log ρ₀(s₀) 是关于 θ 的常数。因此它的导数为 0。
• 求和中的第一个项 P(s_t+1|s_t, a_t) 也与 θ 无关，关于 θ 的导数也是 0。 

去掉方程中的零项后，我们得到（方程5）：

回忆方程2：

方程5计算了方程2右侧第一部分的对数。我们需要将一个项的导数与其对数相关联。我们将使用链式法则和对数导数技巧来实现这一点。

对数导数技巧

我们绕道而行，使用微积分的规则推导一个结果，这将用于简化前面的方程，并使其适合计算方法。

在微积分中，对数的导数可以表示为：

因此，通过重新排列上述方程，x 的导数可以用 x 的对数导数表示：

这有时被称为对数导数技巧。

链式法则

根据链式法则，给定z(y)作为的函数y，其中y本身是θ的函数，y(θ)，则z关于θ的导数为：

在这种情况下，y(θ) 代表 P(θ) 而 z(y) 代表 log(y)。因此，

应用链式法则

我们从微积分中知道d(log(y)) / dy = 1/y。将这个结论用在上述右手边的第一个表达式中。

将 y 移到左手边，并使用 符号：

y 代表 P(θ)。因此，上述方程等价于：

应用对数导数技巧

上述结果给出了方程2（如下所示）右侧的第一个表达式。

利用方程2右侧的结果，我们得到：

我们将右侧积分下的项重新排列如下：

推导最终结果

请注意，上述表达式包含期望的积分展开： ∫P(θ)∇logP(θ) = E[∇logP(θ)]

因此，上述的RHS可以表示为期望：

我们将对数概率的导数代入到期望奖励的表达式中：

在上述方程中，将∇的值代入logP(θ)的方程5中得到：

这是根据策略梯度定理得到的奖励函数梯度的表达式。

策略梯度背后的直觉

策略梯度方法将策略的输出转换为概率分布。代理从这个分布中抽样以选择一个动作。策略梯度方法调整策略参数。这导致在每次迭代中更新这个概率分布。更新后的概率分布更有可能选择导致更高奖励的动作。

策略梯度算法计算期望回报相对于策略参数的梯度。通过沿着这个梯度的方向移动策略参数，代理在训练过程中增加选择导致更高奖励的动作的概率。

本质上，导致更好结果的动作在未来被选择的可能性增加，从而逐步改善策略以最大化长期奖励。

在Python中实现策略梯度

在讨论了策略梯度的基本原理后，我们展示了如何使用PyTorch和Gymnasium来实现它们。

设置环境

第一步，我们需要安装gymnasium以及一些支持库，如NumPy和PyTorch。

要在服务器或本地计算机上安装gymnasium及其依赖项，请运行：

$ pip install gymnasium 

要在Google Colab或DataLab等Notebook中安装，请使用：

!pip install gymnasium

您可以在Python环境中导入这些包：

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

编码一个简单的策略梯度代理

使用.make()方法创建环境的实例。

env = gym.make('CartPole-v1')

与其他机器学习方法一样，我们使用神经网络来实现策略梯度代理。 

CartPole-v1是一个简单的环境，因此我们设计了一个简单的具有64个神经元的隐藏层的网络。输入层的维度等于观察空间的维度。输出层的维度等于环境动作空间的大小。因此，策略网络将观察到的状态映射到动作。给定一个观察作为输入，网络根据策略输出预测的动作。 

下面的代码实现了策略网络： 

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

训练代理

环境在每个时间步根据代理的状态和动作给出奖励。策略梯度方法包括在累积奖励（回报）上运行梯度下降。目标是最大化总回报。 

为了计算一个回合中的回报，您需要累积（带有折扣因子）该回合中所有时间步的奖励。此外，对回报进行归一化有助于确保平稳和稳定的训练。下面的代码展示了如何实现这一点：

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

在每次前向传播迭代中，我们执行以下步骤：

• 根据当前策略使用.step()函数运行代理。策略预测每个时间步骤中选择行动的概率。
• 根据代理的行动从环境中接收奖励。
• 累积逐步奖励和动作的对数概率，直到代理达到终止状态。

以下代码实现了前向传播：

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

使用反向传播和梯度上升来更新策略

在传统机器学习中：

• 损失指预测输出和实际输出之间的差异。
• 我们使用梯度下降来最小化损失。

在强化学习中：

• 损失是一个代理，用于应用梯度下降（或上升）的数量。
• 我们使用梯度上升来最大化回报（累积奖励）。
• 预期回报值被用作梯度下降的损失代理。预期回报值是以下内容的乘积：
• 每个步骤预期的回报与
• 每个步骤中选择采样动作的概率。
• 为了使用反向传播进行梯度上升，我们使用损失的负值。

下面的代码计算损失：

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

与标准机器学习算法类似，为了更新策略，您需要针对损失函数运行反向传播。下面的update_policy()方法调用calculate_loss()方法。然后对此损失运行反向传播以更新策略参数，即策略网络的模型权重。

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

训练循环

我们使用之前定义的函数来训练策略。在开始训练之前，我们需要：

• 一个未训练的策略，初始化为PolicyNetwork类的随机实例。
• 一个使用Adam算法的优化器。
• 折扣因子、学习率、丢弃率、奖励阈值和最大训练周期的超参数。

我们在训练循环中迭代，直到平均回报超过奖励阈值。在每次迭代中，我们执行以下步骤：

• 对于每个回合，运行一次前向传播。收集动作的对数概率、逐步回报和该回合的总回报。将回合回报累积到一个数组中。
• 使用对数概率和逐步回报计算损失。对损失进行反向传播。使用优化器更新策略参数。
• 检查在N_TRIALS内的平均回报是否超过奖励阈值。

下面的代码实现了这些步骤：

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

通过调用main()函数来运行训练程序：

main()

这个 DataLab 工作簿 包含了上述策略梯度算法的实现。 您可以直接运行它，或者将其用作修改算法的起点。

策略梯度方法的优势和挑战

策略梯度方法具有多个优势，例如：

• 处理连续动作空间：基于值的方法（如Q-learning）在处理连续动作空间时效率低下，因为它们需要估计整个动作空间上的值。策略梯度方法可以直接使用期望回报的梯度来优化策略。这种方法在处理连续动作分布时表现良好。因此，策略梯度方法适用于基于连续动作空间的任务，比如基于机器人控制的任务。
• 随机策略：策略梯度方法可以学习随机策略 – 这种策略给出选择每个可能动作的概率。这使得代理可以尝试各种动作，并减少陷入局部最优解的风险。在复杂环境中，代理需要探索动作空间以找到最优策略。随机性有助于平衡探索（尝试新动作）和利用（选择已知最佳动作），这对于存在不确定性或稀疏奖励的环境至关重要。
• 直接策略优化：策略梯度直接优化策略，而不使用值函数。在连续或高维动作空间中，为每个动作逼近值可能会变得计算昂贵。因此，基于策略的方法在这种环境中表现良好。

尽管有许多优点，策略梯度方法也存在一些固有挑战：

• 梯度估计方差高：策略梯度方法通过对概率分布进行采样来选择动作。实际上，它们对轨迹进行采样以估计期望回报。由于采样过程本质上是随机的，因此在后续迭代中估计的回报可能具有很高的方差。这可能会使代理程序难以有效学习，因为策略的更新可能在迭代之间显着波动。
• 训练过程中的不稳定性：
• 策略梯度方法对超参数（如学习率）很敏感。如果学习率过高，策略参数的更新可能过大，导致训练错过最佳参数。另一方面，如果学习率过小，收敛速度可能很慢。
• 策略梯度方法需要平衡探索与利用。如果代理不够探索，可能无法达到最优策略的邻域。相反，如果探索过多，将无法收敛到最优策略，并在动作空间周围振荡。
• 样本效率：策略梯度方法通过执行每个策略直至终止并累积每一步的奖励来估计回报。因此，它们需要与环境进行许多交互以获得大量的样本轨迹。对于状态或动作空间较大的环境来说，这是低效且昂贵的。

稳定性解决方案

由于策略梯度方法中不稳定性是一个相对常见的问题，开发者已经采用各种解决方案来稳定训练过程。下面，我们介绍使用策略梯度来稳定训练的常见解决方案：

使用基准函数

由于采样效率低下，训练迭代过程中估计的回报梯度可能具有较高的方差，导致训练不稳定且缓慢。减少方差的常见方法是使用基线函数，例如优势演员-评论家（A2C）方法。其思想是使用代理（优势函数）来替代估计回报作为目标函数。

优势被计算为从采样轨迹获得的实际回报与给定初始状态的预期回报之间的差异。该方法涉及使用值函数作为状态和状态-动作对的期望值。通过将损失表示为实际回报与预期回报之间的差异，而不是仅仅作为回报，A2C减少了损失函数和梯度中的方差，从而使训练更加稳定。

使用熵正则化

在某些环境中，例如那些具有稀疏奖励（只有很少状态提供奖励）的环境中，策略很快采用确定性方法。它还采用贪婪方法并利用已经探索过的路径。这会阻止进一步的探索，并经常导致收敛到局部最优解和次优策略。

解决方案是鼓励探索，通过对当策略变得过于确定性时施加惩罚来实现。这是通过在目标函数中添加一个基于熵的项来完成的。熵衡量策略中的随机性。熵越大，代理选择的动作中的随机性就越多。这个基于熵的项是熵系数和当前策略熵的乘积。

将熵纳入目标函数有助于在利用和探索之间实现平衡。

策略梯度扩展

在各种策略梯度方法的扩展中，最基本的之一是REINFORCE算法。它提供了策略梯度定理的简单实现，并且是更高级技术的基础。

REINFORCE算法

REINFORCE算法，也被称为蒙特卡洛强化学习，是策略梯度定理的基本实现之一。它使用蒙特卡洛方法来估计回报和策略梯度。在遵循REINFORCE算法时，智能体直接从环境中对所有动作（从初始状态到终止状态）进行采样。这与其他方法（如TD学习和动态规划）形成对比，后者基于值函数估计来引导它们的动作。

下面，我们介绍REINFORCE算法的基本步骤：

• 用随机参数初始化策略
• 重复多个训练周期。对于每个周期：
• 生成整个周期的每个步骤如下：
• 将状态传递给策略函数。
• 策略函数为每个可能的动作生成概率。
• 从该概率分布中随机抽样一个动作。
• 对于剧集中的每个状态，估计直到步骤的收益（折扣累积奖励）。
• 估计目标函数的梯度（根据策略梯度定理），表达为逐步收益与每一步的动作概率的乘积。
• 通过应用梯度更新策略参数。

对于每个策略，您可以抽样单个轨迹来估计梯度（如上所示），或在相同策略下抽样多个轨迹并对梯度进行平均。

演员-评论家方法

演员-评论家方法将策略梯度方法（如REINFORCE）与值函数相结合。

• 演员的工作方式类似于策略梯度方法。演员实施策略，在每一步基于策略选择动作。它通过追踪期望回报的梯度来更新策略。
• 评论家实施值函数，作为基准（在前一节中讨论）。这有助于使训练更加高效和稳定。

策略梯度方法如REINFORCE使用原始回报来估计每条轨迹的梯度。由于采样过程绘制这些轨迹，这可能导致回报和梯度的方差很大。使用优势函数代替原始回报解决了这个问题。优势函数是实际回报与期望回报（即价值函数）之间的差异。演员-评论家方法是一类算法。当评论家使用优势函数进行实现（最常见的方法）时，它也被称为优势演员-评论家（A2C）。

邻近策略优化（PPO）

在复杂环境中，像A2C这样的演员-评论家方法单独无法有效控制回报和梯度的方差。在这种情况下，人为限制每次迭代中策略的变化量会有所帮助。这迫使更新后的（经过梯度上升）策略保持在旧策略的邻域内。

像邻近政策优化这样的方法对策略梯度进行两项修改：

• 使用优势函数。通常，这个优势函数使用值函数作为基准。在这方面，它们类似于A2C方法。
• 限制策略参数在每次迭代中的变化量。这是通过使用修剪的替代目标函数来实现的。算法指定了一个范围，新策略与旧策略之比必须落在其中。当比率（经过梯度更新后）超过这些预定值时，它被修剪为落在此范围内。

因此，PPO显著改进了普通策略梯度方法，在复杂环境中提高了稳定性。剪切的目标函数可以防止回报和梯度的大方差使策略更新失稳。为了在探索和开发之间取得平衡，也可以修改PPO以使用熵正则化。这可以通过向目标函数添加一个熵项（由策略熵乘以一个缩放参数）来实现。

最近的进展

策略梯度是最早用于解决RL问题的方法之一。在快速GPU问世后，各种新方法被提出来将现代机器学习技术应用于策略梯度。

梯度增强强化学习

近年来，将梯度提升等方法应用于强化学习算法取得了进展。梯度提升将多个弱模型的预测结合起来生成一个强模型。这被称为梯度提升强化学习（GBRL）。GBRL是一个类似于XGBoost的Python软件包，它实现了这些技术用于强化学习算法。

迁移强化学习

迁移学习（TL）是一种技术，其中一个模型获取的知识被应用于改善另一个模型的性能。迁移学习很有帮助，因为从头开始训练机器学习模型是昂贵的。TL方法已经与策略梯度结合使用，以改善强化学习模型的性能。这种方法被称为迁移强化学习（TRL）。

结论

政策梯度是解决强化学习问题的最基本方法之一。

在本文中，我们介绍了政策梯度的第一原则，并展示了如何推导政策梯度定理。我们还演示了如何在Gymnasium环境中使用PyTorch实现一个简单的基于梯度的算法。最后，我们讨论了基本政策梯度算法面临的实际挑战和常见扩展。

如果您想深入了解强化学习和PyTorch深度学习，请查看以下课程：

• 强化学习专题 – 从基于价值的方法到政策优化技术，学习强化学习的基础知识。
• PyTorch深度学习入门 – 通过PyTorch获得实践经验，从零开始构建深度学习模型。