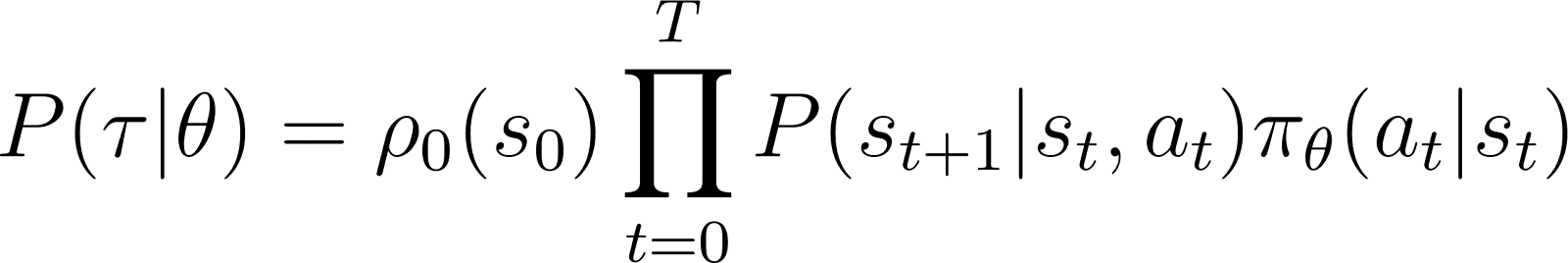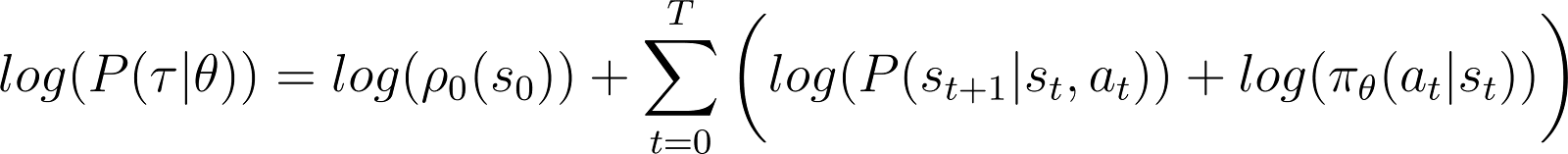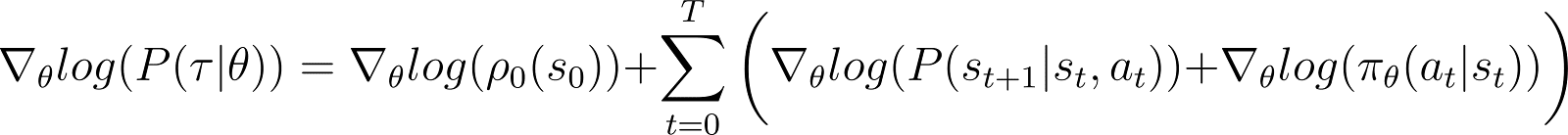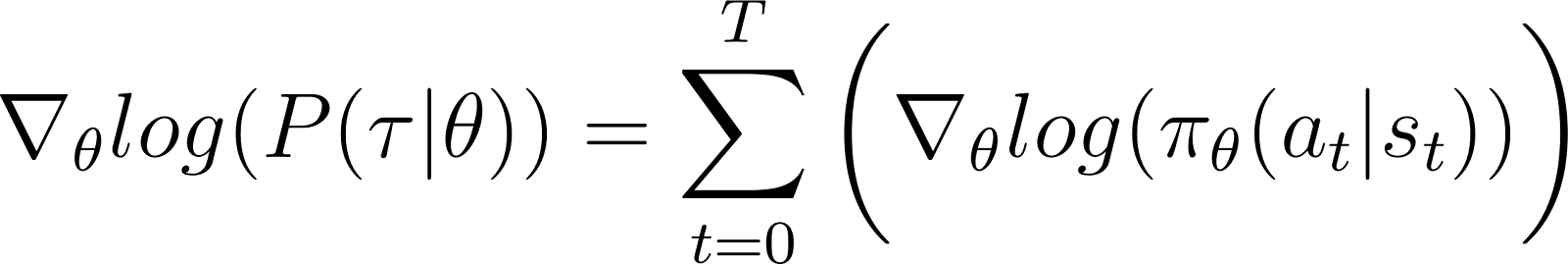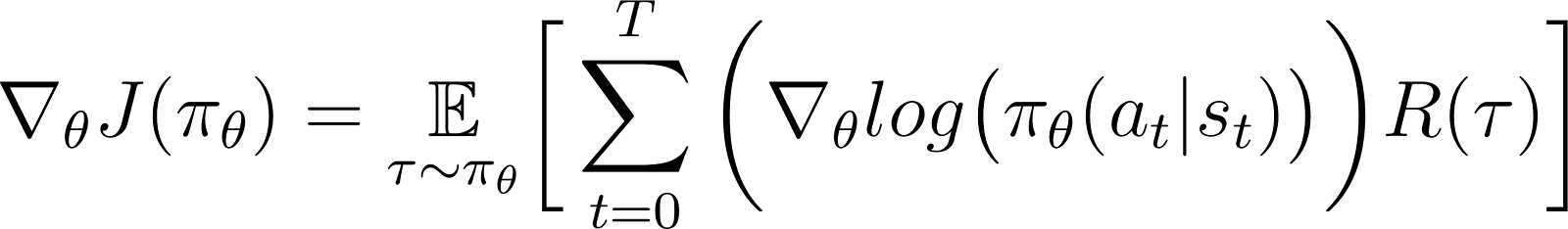Théorème du gradient de la politique expliqué : une introduction pratique

Pourquoi utiliser les méthodes de gradient de politique?

Un avantage clé des méthodes de gradient de politique est leur capacité à gérer des espaces d’actions complexes, là où les approches traditionnelles basées sur la valeur rencontrent des difficultés.

Gestion des espaces d’actions de grande dimension

Les méthodes basées sur la valeur, telles que le Q-learning, fonctionnent en estimant la fonction de valeur pour toutes les actions possibles. Cela devient difficile lorsque l’espace d’action de l’environnement est soit continu, soit discret mais vaste.

Les méthodes de gradient de politique paramètrent la politique et estiment le gradient des récompenses cumulées par rapport aux paramètres de la politique. Elles utilisent ce gradient pour optimiser directement la politique en mettant à jour ses paramètres. Ainsi, elles peuvent gérer efficacement des espaces d’action de haute dimension ou continus. Les gradients de politique sont également à la base des Méthodes d’apprentissage par renforcement utilisant les retours humains (RLHF).

En paramétrant la politique et en ajustant ses paramètres en fonction des gradients, les gradients de politique peuvent gérer efficacement des actions continues et de haute dimension. Cette approche directe permet une meilleure généralisation et une exploration plus flexible, la rendant bien adaptée à des tâches telles que le contrôle robotique et d’autres environnements complexes.

Apprentissage de politiques stochastiques

Étant donné un ensemble d’observations :

• Une politique déterministe spécifie quelle action l’agent prend.
• Une politique stochastique donne un ensemble d’actions et la probabilité pour l’agent de choisir chaque action.

Lorsqu’il suit une politique stochastique, la même observation peut conduire à choisir différentes actions dans différentes itérations. Cela favorise l’exploration de l’espace d’action et empêche la politique de rester bloquée dans des optima locaux. En raison de cela, les politiques stochastiques sont utiles dans les environnements où l’exploration est essentielle pour découvrir le chemin qui mène aux rendements maximaux.

Dans les méthodes basées sur la politique, la sortie de la politique est convertie en une distribution de probabilité, chaque action possible se voyant attribuer une probabilité. L’agent choisit une action en échantillonnant cette distribution, ce qui rend possible la mise en œuvre d’une politique stochastique. Ainsi, les méthodes de gradient de politique combinent l’exploration avec l’exploitation, ce qui est utile dans les environnements avec des structures de récompense complexes.

Dérivation du Théorème du Gradient de Politique

Avant de plonger dans la dérivation, il est important d’établir la notation mathématique et les concepts clés utilisés tout au long de la preuve.

Notation mathématique et préliminaires

Comme mentionné dans une précédente section, le théorème du gradient de politique stipule que la dérivée du rendement attendu est l’espérance du produit du rendement et de la dérivée du logarithme de la politique.

Avant de dériver le théorème du gradient de politique, nous introduisons la notation :

• E[X] se réfère à l’espérance probabiliste d’une variable aléatoire X.
• D’un point de vue mathématique, la politique est exprimée sous forme d’une matrice de probabilité qui donne la probabilité de choisir différentes actions en fonction de différentes observations. Une politique est généralement modélisée comme une fonction paramétrée, avec les paramètres représentés comme θ.
• π_θ fait référence à une politique paramétrée par θ. En pratique, ces paramètres sont les poids du réseau neuronal qui modélise la politique.
• La trajectoire, τ, fait référence à une séquence d’états, commençant généralement par un état initial aléatoire jusqu’à soit le pas de temps actuel soit l’état terminal.
• ∇_θf fait référence au gradient d’une fonction f par rapport au(x) paramètre(s) θ. 
• J(π_θ) fait référence au rendement attendu obtenu par l’agent suivant la politique π_θ. C’est également la fonction objectif pour l’ascension de gradient.
• L’environnement offre une récompense à chaque instant, en fonction de l’action de l’agent. Le retour se réfère aux récompenses cumulées de l’état initial jusqu’à l’instant actuel.
• R(τ) fait référence au rendement généré sur la trajectoire τ.

Étapes de dérivation

Nous montrons comment dériver et prouver le théorème du gradient de politique à partir des premiers principes, en commençant par l’expansion de la fonction objectif et en utilisant l’astuce du log-dérivé.

La fonction objectif (Équation 1)

La fonction objectif dans la méthode du gradient de politique est le rendement

J accumulé en suivant la trajectoire basée sur la politique π exprimée en termes de paramètres θ. Cette fonction objective est donnée comme :

Dans l’équation ci-dessus: 

• Le côté gauche (LHS) est le rendement attendu obtenu en suivant la politique π_θ.
• Le côté droit (RHS) est l’espérance (sur la trajectoire τ générée en suivant la politique π_θ à chaque étape) des retours R(τ) générés sur la trajectoire τ.

Le différentiel de la fonction objective (Équation 2)

Différencier (par rapport à θ) les deux côtés de l’équation ci-dessus donne :

Le gradient de l’espérance (Équation 3)

L’espérance (sur le côté droit) peut être exprimée comme une intégrale sur le produit de :

• La probabilité de suivre une trajectoire τ
• Les rendements générés au cours de la trajectoire τ

Ainsi, le côté droit de l’Équation 2 est reformulé comme suit : 

Le gradient d’une intégrale est égal à l’intégrale du gradient. Ainsi, dans l’expression ci-dessus, nous pouvons amener le gradient ∇_θ sous le signe d’intégrale. Ainsi, le membre de droite devient : 

Ainsi, l’équation 2 peut être réécrite comme :

La probabilité de la trajectoire (Équation 4)

Nous examinons maintenant de plus près P(τ|θ), la probabilité que l’agent suive la trajectoire τ étant donné les paramètres de la politique θ (et donc la politique π_θ). Une trajectoire se compose d’un ensemble d’étapes. Ainsi : 

• La probabilité d’obtenir la trajectoire τ est le produit de:
• La probabilité de suivre toutes les étapes individuelles.

• Au pas de temps t, l’agent passe de l’état s à l’état s_t+1 en suivant l’action a_t. La probabilité que cela se produise est donnée par le produit de :
• La probabilité que la politique prédise l’action a_t dans l’état s_t
• La probabilité de se retrouver dans l’état s_t+1 donné l’action a_t et l’état s_t

Ainsi, en partant d’un état initial s₀, la probabilité que l’agent suive la trajectoire τ en fonction de la politique π_θ est donnée par :

Pour simplifier les choses, nous voulons exprimer le produit dans le RHS ci-dessus comme une somme. Ainsi, nous prenons le logarithme des deux côtés de l’équation ci-dessus :

La dérivée de la log-probabilité (Équation 5) 

Nous prenons maintenant la dérivée (par rapport à θ) de la log-probabilité dans l’équation ci-dessus. 

Dans le RHS de l’équation ci-dessus : 

• Le premier terme log ρ₀(s₀) est constant par rapport à θ. Donc sa dérivée est 0.
• Le premier terme à l’intérieur de la sommation P(s_t+1|s_t, a_t) est également indépendant de θ et sa dérivée par rapport à θ est également nulle. 

En retirant les termes nuls ci-dessus de l’équation, il nous reste (Équation 5):

Rappelez-vous de l’Équation 2 que:

L’Équation 5 évalue le logarithme de la première partie du RHS de l’Équation 2. Nous devons relier la dérivée d’un terme à son logarithme. Nous le faisons en utilisant la règle de la chaîne et l’astuce de la dérivée logarithmique.

L’astuce de la dérivée logarithmique

Nous faisons un détour et utilisons les règles du calcul pour dériver un résultat, que nous utiliserons pour simplifier l’équation précédente et la rendre adaptée aux méthodes de calcul.

En calcul, la dérivée d’un logarithme peut s’exprimer comme suit:

Ainsi, en réarrangeant l’équation ci-dessus, la dérivée de x peut être exprimée en termes de la dérivée du logarithme de x:

Ceci est parfois appelé le tour de la dérivée logarithmique.

La règle de la chaîne

Selon la règle de la chaîne, étant donné z(y) en fonction de y, où y est lui-même une fonction de θ, y(θ), la dérivée de z par rapport à θ est donnée par :

Dans ce cas, y(θ) représente P(θ) et z(y) représente log(y). Ainsi, 

Appliquer la règle de la chaîne

Nous savons en calcul que d(log(y)) / dy = 1/y. Utilisez ceci dans la première expression du côté droit ci-dessus. 

Déplacer y vers le côté gauche et utiliser la notation :

y représente P(θ). Donc, l’équation ci-dessus est équivalente à:

Appliquant le truc de la dérivée logarithmique

Le résultat ci-dessus donne la première expression du membre de droite de l’Équation 2 (montrée ci-dessous).

En utilisant le résultat dans le membre de droite de l’Équation 2, nous obtenons :

Nous réarrangeons les termes sous l’intégrale du membre de droite comme suit :

Dérivant le résultat final

Remarquez que l’expression ci-dessus contient le développement intégral d’une attente: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

Ainsi, le RHS ci-dessus peut être exprimé comme l’espérance :

Nous substituons la dérivée de la probabilité logarithmique dans l’expression de la récompense attendue :

Dans l’équation ci-dessus, substituez la valeur de ∇logP(θ) de l’équation 5 pour obtenir:

Ceci est l’expression du gradient de la fonction de récompense selon le théorème du gradient de la politique.

L’intuition derrière le gradient de la politique

Les méthodes de gradient de la politique convertissent la sortie de la politique en une distribution de probabilité. L’agent échantillonne cette distribution pour choisir une action. Les méthodes de gradient de la politique ajustent les paramètres de la politique. Cela conduit à la mise à jour de cette distribution de probabilité à chaque itération. La distribution de probabilité mise à jour a une probabilité plus élevée de choisir des actions qui entraînent des récompenses plus élevées.

L’algorithme du gradient de la politique calcule le gradient du rendement attendu par rapport aux paramètres de la politique. En déplaçant les paramètres de la politique dans la direction de ce gradient, l’agent augmente la probabilité de choisir des actions qui résultent en des récompenses plus élevées pendant l’entraînement.

Essentiellement, les actions qui ont conduit à de meilleurs résultats deviennent plus susceptibles d’être choisies à l’avenir, améliorant progressivement la politique pour maximiser les récompenses à long terme.

Mise en œuvre des gradients de politique en Python

Ayant discuté des principes fondamentaux des gradients de politique, nous montrons comment les implémenter en utilisant PyTorch et Gymnasium.

Mise en place de l’environnement

Comme première étape, nous devons installer gymnasium et quelques bibliothèques de support comme NumPy et PyTorch.

Pour installer gymnasium et ses dépendances sur un serveur ou une machine locale, exécutez :

$ pip install gymnasium 

Pour installer en utilisant un cahier comme Google Colab ou DataLab, utilisez :

!pip install gymnasium

Vous importez ces packages dans l’environnement Python :

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

Programmation d’un agent simple de gradient de politique

Créez une instance de l’environnement en utilisant la méthode .make().

env = gym.make('CartPole-v1')

Comme pour d’autres méthodes d’apprentissage automatique, nous utilisons un réseau de neurones pour implémenter l’agent de gradient de politique.

CartPole-v1 est un environnement simple, donc nous concevons un réseau simple avec 1 couche cachée de 64 neurones. La dimension de la couche d’entrée est égale aux dimensions de l’espace d’observation. La dimension de la couche de sortie est égale à la taille de l’espace d’action de l’environnement. Ainsi, le réseau de politique associe les états observés à des actions. Étant donné une observation en entrée, le réseau produit l’action prédite selon la politique.

Le code ci-dessous implémente le réseau de politique :

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

Formation de l’agent

L’environnement attribue une récompense à chaque instant en fonction de l’état et de l’action de l’agent. L’approche de gradient de politique consiste à exécuter la descente de gradient sur les récompenses cumulées (retour). L’objectif est de maximiser le retour total.

Pour calculer le retour dans un épisode, vous accumulez (avec un facteur d’actualisation) les récompenses de tous les instants de cet épisode. De plus, normaliser les retours est utile pour garantir un entraînement fluide et stable. Le code ci-dessous montre comment faire cela :

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

À chaque itération de la passe avant, nous effectuons les étapes suivantes :

• Exécutez l’agent en fonction de la politique actuelle en utilisant la fonction .step(). La politique prédit la probabilité de prendre l’action choisie à chaque instant.
• Recevez la récompense de l’environnement en fonction de l’action de l’agent.
• Accumulatez les récompenses étape par étape et les probabilités logarithmiques des actions jusqu’à ce que l’agent atteigne un état terminal.

Le code ci-dessous implémente la passe avant :

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

Utilisation de la rétropropagation et de la montée de gradient pour mettre à jour la politique

Dans l’apprentissage machine traditionnel :

• La perte fait référence à la différence entre la sortie prédite et la sortie réelle.
• Nous minimisons la perte en utilisant la descente de gradient.

Dans l’AR :

• La perte est un proxy pour la quantité sur laquelle l’**algorithme de descente (ou montée) de gradient** est appliqué. 
• Nous maximisons le rendement (récompenses cumulatives) en utilisant la montée de gradient.
• La valeur de rendement attendue est utilisée comme proxy pour la perte de la descente de gradient. La valeur de rendement attendue est le produit de :
• Les rendements attendus à chaque étape avec 
• La probabilité de choisir l’action échantillonnée à chaque étape. 
• Pour appliquer la montée de gradient en utilisant la rétropropagation, nous utilisons le négatif de la perte. 

Le code ci-dessous calcule la perte :

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

Similaire aux algorithmes de **machine learning** standards, pour mettre à jour la politique, vous exécutez la rétropropagation par rapport à la fonction de perte. La méthode update_policy() ci-dessous appelle la méthode calculate_loss(). Ensuite, elle exécute la rétropropagation sur cette perte pour mettre à jour les paramètres de la politique, c’est-à-dire les poids du modèle du réseau de politique. 

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

La boucle d’entraînement

Nous utilisons les fonctions définies précédemment pour entraîner la politique. Avant de commencer l’entraînement, nous avons besoin de : 

• Une politique non entraînée initialisée comme une instance aléatoire de la classe PolicyNetwork. 
• Un optimiseur qui utilise l’algorithme Adam. 
• Des hyperparamètres pour le facteur de réduction, le taux d’apprentissage, le taux de dropout, le seuil de récompense, et le nombre maximum d’époques d’entraînement. 

Nous itérons à travers la boucle d’entraînement jusqu’à ce que le rendement moyen dépasse le seuil de récompense. À chaque itération, nous exécutons les étapes suivantes : 

• Pour chaque épisode, exécutez le passage avant une fois. Collectez la probabilité logarithmique des actions, les rendements étape par étape, et le rendement total de cet épisode. Accumulez les rendements épisodiques dans un tableau. 
• Calculez la perte en utilisant les probabilités logarithmiques et les rendements étape par étape. Exécutez la rétropropagation sur la perte. Utilisez l’optimiseur pour mettre à jour les paramètres de la politique. 
• Vérifiez si le rendement moyen sur N_TRIALS dépasse le seuil de récompense. 

Le code ci-dessous implémente ces étapes :

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

Exécutez le programme de formation en appelant la fonction main(). :

main()

Ce classeur DataLab contient l’implémentation ci-dessus de l’algorithme de gradient de politique. Vous pouvez l’exécuter directement ou l’utiliser comme point de départ pour modifier l’algorithme.

Avantages et défis des méthodes de gradient de politique

Les méthodes de gradient de politique offrent plusieurs avantages, tels que :

• Gestion des espaces d’actions continus: Les méthodes basées sur la valeur (comme le Q-learning) sont inefficaces avec des espaces d’actions continus car elles doivent estimer les valeurs sur l’ensemble de l’espace d’actions. Les méthodes de gradient de politique peuvent optimiser directement la politique en utilisant le gradient des rendements attendus. Cette approche fonctionne bien avec les distributions d’actions continues. Ainsi, les méthodes de gradient de politique conviennent aux tâches telles que le contrôle robotique qui sont basées sur des espaces d’actions continus.
• Politiques stochastiques: Les méthodes de gradient de politique peuvent apprendre des politiques stochastiques – qui donnent une probabilité de sélection pour chaque action possible. Cela permet à l’agent d’essayer une variété d’actions et réduit le risque de rester bloqué dans des optima locaux. Cela aide dans des environnements complexes où l’agent doit explorer l’espace d’actions pour trouver la politique optimale. La nature stochastique aide à équilibrer l’exploration (essayer de nouvelles actions) et l’exploitation (choisir les actions les mieux connues), ce qui est crucial pour les environnements avec de l’incertitude ou des récompenses rares.
• Optimisation directe de la politique: Les gradients de politique optimisent directement la politique au lieu d’utiliser des fonctions de valeur. Dans des espaces d’actions continus ou de grande dimension, l’approximation des valeurs pour chaque action peut devenir computationnellement coûteuse. Ainsi, les méthodes basées sur la politique fonctionnent bien dans de tels environnements.

Malgré leurs nombreux avantages, les méthodes de gradient de politique présentent certains défis inhérents:

• Haute variance dans les estimations de gradient: Les méthodes de gradient de politique sélectionnent des actions en échantillonnant une distribution de probabilité. En effet, elles échantillonnent la trajectoire pour estimer le rendement attendu. En raison du caractère aléatoire intrinsèque du processus d’échantillonnage, les rendements estimés dans les itérations suivantes peuvent présenter une forte variance. Cela peut rendre difficile l’apprentissage efficace de l’agent car les mises à jour de la politique peuvent fluctuer significativement entre les itérations. 
• Instabilité pendant l’entraînement: 
• Les méthodes de gradient de politique sont sensibles aux hyperparamètres comme le taux d’apprentissage. Si le taux d’apprentissage est trop élevé, les mises à jour des paramètres de la politique peuvent être trop importantes, ce qui peut faire en sorte que l’entraînement passe à côté des paramètres optimaux. D’un autre côté, si le taux d’apprentissage est trop faible, la convergence peut être lente. 
• Les méthodes de gradient de politique doivent équilibrer l’exploration et l’exploitation. Si l’agent n’explore pas suffisamment, il peut ne pas atteindre le voisinage de la politique optimale. En revanche, s’il explore trop, il ne convergera pas vers la politique optimale et oscillera autour de l’espace d’action.
• Manque d’efficacité des échantillons: Les méthodes de gradient de politique estiment le rendement en suivant chaque politique jusqu’à la terminaison et en accumulant les récompenses à chaque étape. Ainsi, elles nécessitent de nombreuses interactions avec l’environnement pour générer un grand nombre de trajectoires d’échantillonnage. Cela est inefficace et coûteux pour les environnements avec de grands espaces d’états ou d’actions.

Solutions pour la stabilité

Étant donné que l’instabilité est un problème relativement courant dans les méthodes de gradient de politique, les développeurs ont adopté diverses solutions pour stabiliser le processus d’entraînement. Ci-dessous, nous présentons des solutions courantes pour stabiliser l’entraînement en utilisant des gradients de politique :

Utilisation de fonctions de base

En raison d’un échantillonnage inefficace, les gradients des rendements estimés pendant les itérations d’entraînement peuvent avoir une variance élevée, rendant l’entraînement instable et lent. Une approche courante pour réduire la variance consiste à utiliser des fonctions de référence, telles que la méthode Advantage Actor-Critic (A2C). L’idée est d’utiliser un proxy (la fonction d’avantage) au lieu du rendement estimé pour la fonction objectif.

L’avantage est calculé comme la différence entre le rendement réel de la trajectoire échantillonnée et le rendement attendu donné l’état initial. Cette approche implique l’utilisation de la fonction de valeur comme valeur attendue des états et des paires état-action. En représentant la perte comme la différence entre le rendement réel et le rendement attendu plutôt qu’en tant que rendements seuls, A2C réduit la variance dans la fonction de perte et, par conséquent, dans les gradients, rendant l’entraînement plus stable.

Utilisation de la régularisation par entropie

Dans certains environnements, tels que ceux avec des récompenses rares (seulement très peu d’états donnent une récompense), la politique adopte rapidement une approche déterministe. Elle adopte également une approche avare et exploite les chemins qu’elle a déjà explorés. Cela empêche une exploration supplémentaire et conduit souvent à une convergence vers des optima locaux et des politiques sous-optimales.

La solution consiste à encourager l’exploration sans pénaliser la politique lorsqu’elle devient trop déterministe. Cela se fait en ajoutant un terme basé sur l’entropie à la fonction objective. L’entropie mesure le degré de hasard dans la politique. Plus l’entropie est grande, plus il y a de hasard dans les actions choisies par l’agent. Ce terme basé sur l’entropie est le produit du coefficient d’entropie et de l’entropie de la politique actuelle.

Intégrer l’entropie dans la fonction objective permet d’atteindre un équilibre entre l’exploitation et l’exploration.

Extensions de la méthode des gradients de politique

Parmi les diverses extensions des méthodes de gradients de politique, l’une des plus fondamentales est l’algorithme REINFORCE. Il offre une mise en œuvre simple du théorème des gradients de politique et sert de base pour des techniques plus avancées.

Algorithme REINFORCE

L’algorithme REINFORCE, également connu sous le nom de Monte Carlo Reinforce, est l’une des implémentations de base du théorème du gradient de politique. Il utilise des méthodes de Monte Carlo pour estimer les rendements et les gradients de politique. En suivant l’algorithme REINFORCE, l’agent échantillonne directement toutes les actions (de l’état initial à l’état terminal) de l’environnement. Cela contraste avec d’autres méthodes comme l’apprentissage par renforcement temporel et la programmation dynamique, qui amorcent leurs actions en fonction des estimations de la fonction de valeur.

Voici les étapes de base de l’algorithme REINFORCE :

• Initialiser la politique avec des paramètres aléatoires
• Répéter plusieurs épisodes d’entraînement. Pour chaque épisode :
• Générer chaque étape de l’épisode entier comme suit :
• Transmettre l’état à la fonction de politique.
• La fonction de politique génère des probabilités pour chaque action possible.
• Échantillonner aléatoirement une action à partir de cette distribution de probabilités.
• Pour chaque état de l’épisode, estimer les retours (récompenses cumulatives actualisées) jusqu’à l’étape.
• Estimer le gradient de la fonction objectif (selon le théorème du gradient de la politique), exprimé comme le produit des retours étape par étape et des probabilités d’action pour chaque étape.
• Mettre à jour les paramètres de la politique en appliquant les gradients.

Pour chaque politique, vous pouvez échantillonner une seule trajectoire pour estimer le gradient (comme indiqué ci-dessus) ou moyenne le gradient sur plusieurs trajectoires échantillonnées sous la même politique.

Méthodes acteur-critique

Les méthodes acteur-critique combinent les méthodes de gradient de politique (comme REINFORCE) avec des fonctions de valeur.

• Le fonctionnement de l’acteur est similaire aux méthodes de gradient de politique. L’acteur met en œuvre la politique, sélectionnant des actions à chaque étape en fonction de la politique. Il met à jour la politique en suivant le gradient du rendement attendu.
• Le critique met en œuvre la fonction de valeur, qui est utilisée comme une référence (discutée dans la section précédente). Cela aide à rendre l’entraînement plus efficace et stable.

Les méthodes de gradient de politique comme REINFORCE estiment les gradients le long de chaque trajectoire en utilisant le rendu brut. Parce qu’un processus d’échantillonnage tire ces trajectoires, cela peut entraîner de grandes variances dans les rendus et gradients. Utiliser une fonction d’avantage au lieu des rendus bruts résout ce problème. La fonction d’avantage est la différence entre les rendus réels et attendus (c’est-à-dire la fonction de valeur). Les méthodes acteur-critique sont une classe d’algorithmes. Lorsque le critique est implémenté en utilisant la fonction d’avantage (l’approche la plus courante), on l’appelle également acteur-critique à avantage (A2C).

Optimisation de politique proximale (PPO)

Dans des environnements complexes, les méthodes acteur-critique comme A2C seules ne suffisent pas à contrôler la variance dans les rendus et gradients. Dans de tels cas, limiter artificiellement la quantité par laquelle la politique peut changer à chaque itération aide. Cela oblige la politique mise à jour (après l’ascension de gradient) à se situer à proximité de l’ancienne politique.

Des méthodes comme l’optimisation proximale de politique apportent deux modifications aux gradients de politique:

• Utilisez une fonction d’avantage. Généralement, cette fonction d’avantage utilise la fonction de valeur comme référence. À cet égard, elles sont similaires aux méthodes A2C. 
• Restreignez la quantité de changement des paramètres de la politique à chaque itération. Cela se fait en utilisant une fonction objectif auxiliaire tronquée. L’algorithme spécifie une plage dans laquelle le ratio de la nouvelle politique par rapport à l’ancienne politique doit se situer. Lorsque le ratio (après la mise à jour du gradient) dépasse ces valeurs prédéterminées, il est tronqué pour se situer dans la plage. 

Ainsi, le PPO améliore significativement les méthodes de gradient de politique vanille, ce qui améliore la stabilité dans des environnements complexes. La fonction objectif tronquée empêche les grandes variances dans les retours et les gradients de déstabiliser les mises à jour de la politique. Pour trouver un équilibre entre l’exploration et l’exploitation, il est également possible de modifier le PPO pour utiliser une régularisation de l’entropie. Cela se fait en ajoutant un terme d’entropie (un paramètre d’échelle multiplié par l’entropie de la politique) à la fonction objectif.

Récents progrès

Les gradients de politique font partie des premières méthodes utilisées pour résoudre les problèmes de RL. Après l’avènement des GPU rapides, diverses nouvelles approches ont été proposées pour appliquer les techniques ML modernes aux gradients de politique.

Apprentissage par Renforcement Boosté par Gradients

Ces dernières années, des progrès ont été réalisés dans l’application de méthodes telles que le gradient boosting aux algorithmes d’apprentissage par renforcement (RL). Le gradient boosting combine les prédictions de plusieurs modèles faibles pour générer un modèle fort unique. Cela est appelé l’apprentissage par renforcement amélioré par gradient (GBRL). GBRL est un paquet Python similaire à XGBoost qui implémente ces techniques pour les algorithmes RL.

Apprentissage par transfert 

L’apprentissage par transfert (TL) est une technique où les connaissances acquises par un modèle sont appliquées pour améliorer les performances d’un autre modèle. L’apprentissage par transfert est utile car entraîner des modèles d’apprentissage automatique (ML) depuis le début est coûteux. Les approches TL ont été utilisées avec des gradients de politique pour améliorer les performances des modèles RL. Cette approche est appelée L’apprentissage par renforcement par transfert (TRL).

Conclusion

Les gradients de politique font partie des approches les plus fondamentales pour résoudre les problèmes de RL.

Dans cet article, nous avons présenté les premiers principes des gradients de politique et montré comment dériver le théorème du gradient de politique. Nous avons également démontré comment implémenter un algorithme simple basé sur les gradients en utilisant PyTorch dans un environnement de Gymnasium. Enfin, nous avons discuté des défis pratiques et des extensions courantes à l’algorithme de gradient de politique de base.

Si vous souhaitez approfondir votre compréhension de l’apprentissage par renforcement et de l’apprentissage profond avec PyTorch, consultez ces cours :

• Parcours d’apprentissage par renforcement – Apprenez les fondements du RL, des méthodes basées sur la valeur aux techniques d’optimisation de politique.
• Introduction à l’apprentissage profond avec PyTorch – Obtenez une expérience pratique avec PyTorch et construisez des modèles d’apprentissage profond à partir de zéro.