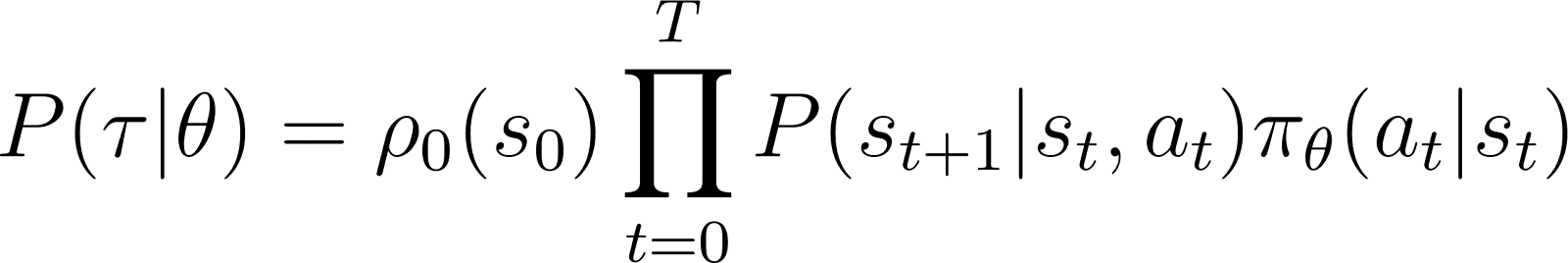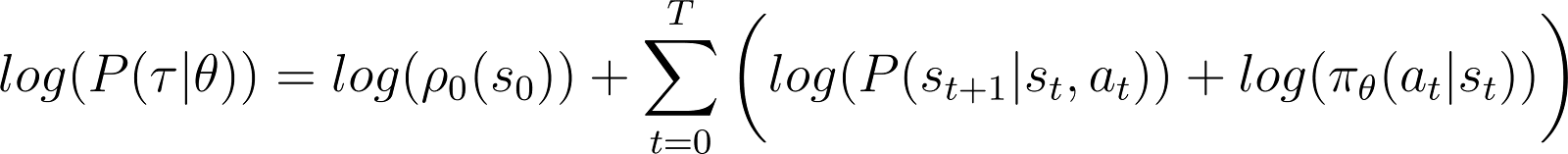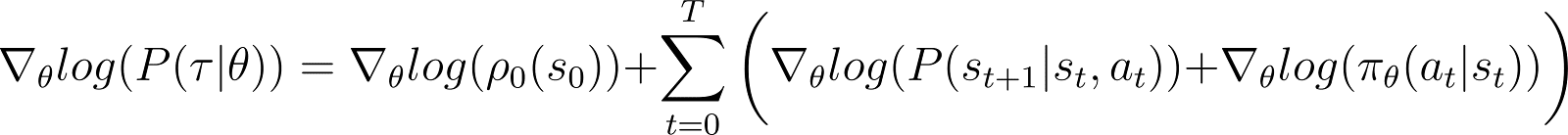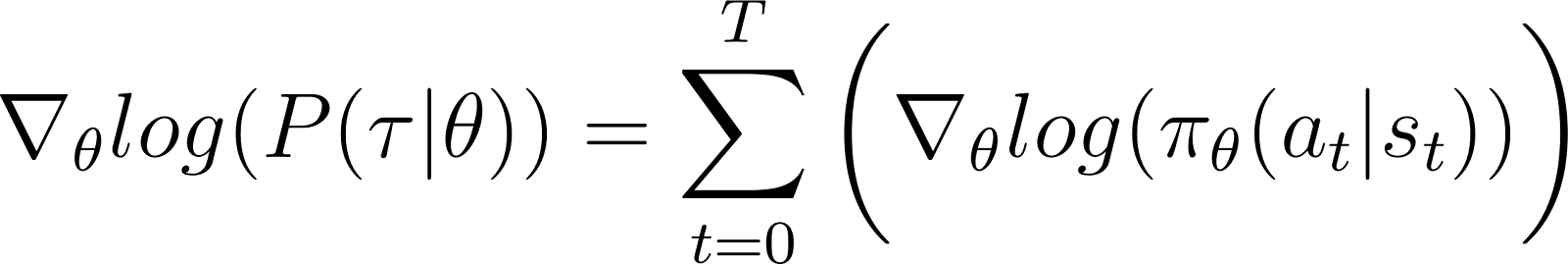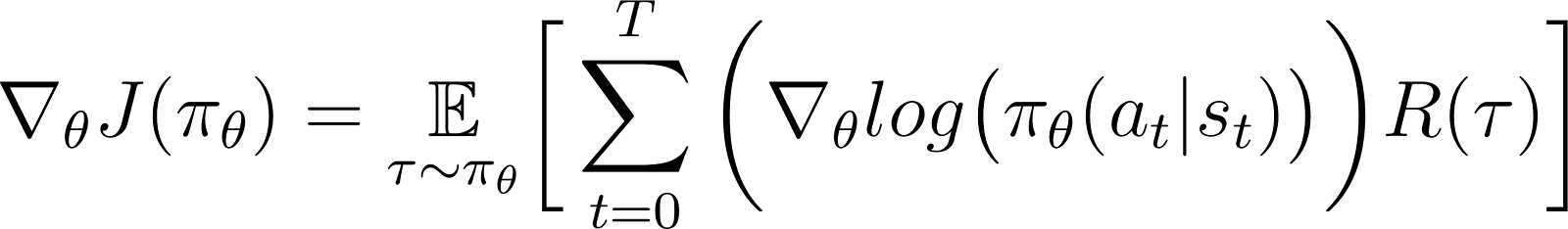Teorema del Gradiente della Politica Spiegato: Un’introduzione pratica

Perché utilizzare i metodi di gradiente della politica?

Un vantaggio chiave dei metodi di gradiente della politica è la loro capacità di gestire spazi azionari complessi, dove gli approcci tradizionali basati sul valore fanno fatica.

Gestire spazi azionari ad alta dimensione

I metodi basati sul valore, come il Q-learning, funzionano stimando la funzione valore per tutte le azioni possibili. Questo diventa difficile quando lo spazio delle azioni dell’ambiente è continuo o discreto ma grande.

I metodi di gradiente della politica parametrizzano la politica e stimano il gradiente delle ricompense cumulative rispetto ai parametri della politica. Usano questo gradiente per ottimizzare direttamente la politica aggiornando i suoi parametri. Pertanto, possono gestire in modo efficiente spazi di azione ad alta dimensione o continui. I gradienti della politica sono anche alla base dei metodi di Apprendimento per Rinforzo con Feedback Umano (RLHF).

Parametrizzando la politica e regolando i suoi parametri in base ai gradienti, i gradienti della politica possono gestire in modo efficiente azioni continue e ad alta dimensione. Questo approccio diretto consente una migliore generalizzazione e un’esplorazione più flessibile, rendendolo adatto per compiti come il controllo robotico e altri ambienti complessi.

Apprendimento di politiche stocastiche

Data una serie di osservazioni:

• Una politica deterministica specifica quale azione l’agente intraprende.
• Una politica stocastica fornisce un insieme di azioni e la probabilità che l’agente scelga ciascuna azione.

Seguendo una politica stocastica, la stessa osservazione può portare a scegliere azioni diverse in iterazioni diverse. Questo favorisce l’esplorazione dello spazio delle azioni e impedisce alla politica di rimanere bloccata in ottimi locali. Per questo motivo, le politiche stocastiche sono utili in ambienti in cui l’esplorazione è essenziale per scoprire il percorso che porta ai massimi ritorni.

Nei metodi basati sulla politica, l’output della politica viene convertito in una distribuzione di probabilità, con ogni azione possibile assegnata a una probabilità. L’agente sceglie un’azione campionando questa distribuzione, rendendo possibile implementare una politica stocastica. Pertanto, i metodi di gradiente della politica combinano esplorazione ed sfruttamento, utili in ambienti con strutture di ricompensa complesse.

Derivazione del Teorema del Gradiente della Politica

Prima di immergersi nella derivazione, è importante stabilire la notazione matematica e i concetti chiave utilizzati nel corso della dimostrazione.

Notazione matematica e preliminari

Come accennato in una sezione precedente, il teorema del gradiente della politica afferma che la derivata del rendimento atteso è l’aspettativa del prodotto del rendimento e della derivata del logaritmo della politica.

Prima di derivare il teorema del gradiente della politica, introduciamo la notazione:

• E[X] si riferisce all’aspettativa probabilistica di una variabile casuale X.
• Matematicamente, la politica è espressa come una matrice di probabilità che fornisce la probabilità di scegliere diverse azioni in base a diverse osservazioni. Una politica è tipicamente modellata come una funzione parametrizzata, con i parametri rappresentati come θ.
• π_θ si riferisce a una politica parametrizzata da θ. In pratica, questi parametri sono i pesi della rete neurale che modella la politica.
• La traiettoria, τ, si riferisce a una sequenza di stati, in genere a partire da uno stato iniziale casuale fino al tempo corrente o allo stato terminale.
• ∇_θf si riferisce al gradiente di una funzione f rispetto al parametro(i) θ.
• J(π_θ) si riferisce al rendimento atteso ottenuto dall’agente seguendo la politica π_θ. Questa è anche la funzione obiettivo per la salita del gradiente.
• L’ambiente fornisce una ricompensa ad ogni passo temporale, a seconda dell’azione dell’agente. Il ritorno si riferisce alle ricompense cumulative dallo stato iniziale al passo temporale corrente.
• R(τ) si riferisce al rendimento generato lungo il percorso τ.

Passaggi di derivazione

Mostriamo come derivare e dimostrare il teorema del gradiente della politica a partire dai principi fondamentali, iniziando con l’espansione della funzione obiettivo e utilizzando il trucco della derivata logaritmica.

La funzione obiettivo (Equazione 1)

La funzione obiettivo nel metodo del gradiente della politica è il ritorno

Jaccumulato seguendo la traiettoria basata sulla politica π espressa in termini di parametri θ. Questa funzione obiettivo è data da:

Nell’equazione sopra:

• Il lato sinistro (LHS) è il rendimento atteso ottenuto seguendo la politica π_θ.
• Il lato destro (RHS) è l’aspettativa (sulla traiettoria τ generata seguendo la politica π_θ in ogni passo) dei ritorni R(τ) generati sulla traiettoria τ.  

Il differenziale della funzione obiettivo (Equazione 2)

Differenziando (rispetto a θ) entrambi i lati dell’equazione precedente si ottiene:

Il gradiente dell’aspettazione (Equazione 3)

L’aspettazione (nel lato destro) può essere espressa come un integrale sul prodotto di:

• La probabilità di seguire una traiettoria τ
• I rendimenti generati lungo la traiettoria τ

Quindi, il lato destro dell’Equazione 2 viene riformulato come:

Il gradiente di un integrale è uguale all’integrale del gradiente. Quindi, nell’espressione sopra, possiamo portare il gradiente ∇_θ sotto il segno dell’integrale. Quindi, il lato destro diventa:

Quindi, l’Equazione 2 può essere riscritta come:

La probabilità della traiettoria (Equazione 4)

Ora diamo un’occhiata più da vicino a P(τ|θ), la probabilità che l’agente segua la traiettoria τ date le condizioni del policy θ (e quindi la policy π_θ). Una traiettoria consiste in un insieme di passi. Quindi: 

• La probabilità di ottenere la traiettoria τ è il prodotto di:
• La probabilità di seguire tutti i singoli passaggi.

• Nel passo di tempo t, l’agente passa dallo stato s allo stato s_t+1 seguendo l’azione a_t. La probabilità che ciò accada è data dal prodotto di:
• La probabilità della politica che predice l’azione a_t nello stato s_t
• La probabilità di finire nello stato s_t+1 dato l’azione a_t e lo stato s_t

Quindi, partendo da uno stato iniziale s₀, la probabilità che l’agente segua la traiettoria τ basata sulla politica π_θ è data da:

Per semplificare le cose, vogliamo esprimere il prodotto nel RHS sopra come una somma. Quindi, prendiamo il logaritmo di entrambi i lati dell’equazione sopra:

La derivata della log-probabilità (Equazione 5) 

Ora prendiamo la derivata (rispetto a θ) della log-probabilità nell’equazione sopra. 

Nel RHS dell’equazione sopra: 

• Il primo termine log ρ₀(s₀) è costante rispetto a θ. Quindi la sua derivata è 0.
• Il primo termine all’interno della sommatoria P(s_t+1|s_t, a_t) è anch’esso indipendente da θ e la sua derivata rispetto a θ è anch’essa 0.

Rimuovendo i termini zero sopra citati dall’equazione, rimaniamo con (Equazione 5):

Ricordiamo dall’Equazione 2 che:

L’Equazione 5 valuta il logaritmo della prima parte del lato destro dell’Equazione 2. Dobbiamo collegare la derivata di un termine con il suo logaritmo. Facciamo ciò utilizzando la regola della catena e il trucco della derivata del logaritmo.

Il trucco della derivata del logaritmo

Facciamo una deviazione e utilizziamo le regole del calcolo per derivare un risultato, che useremo per semplificare l’equazione precedente e renderla adatta ai metodi computazionali.

Nel calcolo, la derivata di un logaritmo può essere espressa come:

Così, riarrangiando l’equazione sopra, la derivata di x può essere espressa in termini della derivata del logaritmo di x:

Questo è a volte chiamato il trucco della log-derivata.

La regola della catena

Secondo la regola della catena, dato z(y) come funzione di y, dove y è a sua volta una funzione di θ, y(θ), la derivata di z rispetto a θ è data da:

In questo caso, y(θ) sta per P(θ) e z(y) sta per log(y). Quindi, 

Applicando la regola della catena

Sappiamo dalla matematica che d(log(y)) / dy = 1/y. Usa questo nella prima espressione del lato destro sopra.

Sposta y a sinistra e usa la notazione:

y sta per P(θ). Quindi l’equazione sopra è equivalente a:

Applicando il trucco del logaritmo-derivato

Il risultato sopra riportato fornisce la prima espressione del lato destro dell’Equazione 2 (mostrata di seguito).

Utilizzando il risultato nel lato destro dell’Equazione 2, otteniamo:

Riorganizziamo i termini sotto l’integrale del lato destro come segue:

Derivando il risultato finale

Osserva che l’espressione sopra contiene lo sviluppo integrale di un’aspettativa: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

Quindi, il lato destro dell’equazione sopra può essere espresso come l’aspettativa:

Sostituiamo la derivata della probabilità logaritmica nell’espressione del premio atteso:

Nell’equazione sopra, sostituisci il valore di ∇logP(θ) dall’Equazione 5 per ottenere: 

Questa è l’espressione per il gradiente della funzione di ricompensa secondo il teorema del gradiente della politica.

L’intuizione dietro il gradiente della politica

I metodi del gradiente della politica convertono l’output della politica in una distribuzione di probabilità. L’agente campiona questa distribuzione per scegliere un’azione. I metodi del gradiente della politica regolano i parametri della politica. Questo porta ad aggiornare questa distribuzione di probabilità in ogni iterazione. La distribuzione di probabilità aggiornata ha una maggiore probabilità di scegliere azioni che portano a ricompense più elevate.

L’algoritmo del gradiente della politica calcola il gradiente del ritorno atteso rispetto ai parametri della politica. Spostando i parametri della politica nella direzione di questo gradiente, l’agente aumenta la probabilità di scegliere azioni che portano a ricompense più elevate durante l’addestramento.

Fondamentalmente, le azioni che hanno portato a risultati migliori diventano più probabili da scegliere in futuro, migliorando gradualmente la politica per massimizzare le ricompense a lungo termine.

Implementazione dei Gradienti della Politica in Python

Dopo aver discusso i principi fondamentali dei gradienti di policy, mostriamo come implementarli usando PyTorch e Gymnasium.

Preparare l’ambiente

Come primo passo, è necessario installare gymnasium e alcune librerie di supporto come NumPy e PyTorch.

Per installare gymnasium e le sue dipendenze su un server o una macchina locale, eseguire:

$ pip install gymnasium 

Per installare utilizzando un Notebook come Google Colab o DataLab, utilizzare:

!pip install gymnasium

È necessario importare questi pacchetti all’interno dell’ambiente Python:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

Implementazione di un semplice agente con gradienti di policy

Creare un’istanza dell’ambiente utilizzando il metodo .make().

env = gym.make('CartPole-v1')

Come per gli altri metodi di apprendimento automatico, utilizziamo una rete neurale per implementare l’agente del gradiente di policy.

CartPole-v1 è un ambiente semplice, quindi progettiamo una rete semplice con 1 strato nascosto con 64 neuroni. La dimensione dello strato di input è uguale alle dimensioni dello spazio di osservazione. La dimensione dello strato di output è uguale alla dimensione dello spazio delle azioni dell’ambiente. Pertanto, la rete di policy mappa gli stati osservati alle azioni. Dato un’osservazione in input, la rete restituisce l’azione prevista secondo la policy.

Il codice sottostante implementa la rete di policy:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

Allenare l’agente

L’ambiente fornisce una ricompensa ad ogni passo temporale a seconda dello stato e dell’azione dell’agente. L’approccio del gradiente di policy consiste nell’eseguire discesa del gradiente sulle ricompense cumulative (return). L’obiettivo è massimizzare il rendimento totale.

Per calcolare il rendimento in un episodio, si accumulano (con un fattore di sconto) le ricompense di tutti i passaggi temporali in quell’episodio. Inoltre, normalizzare i rendimenti è utile per garantire un addestramento uniforme e stabile. Il codice sottostante mostra come fare ciò:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

Ad ogni iterazione del passaggio in avanti, eseguiamo i seguenti passaggi:

• Esegui l’agente basato sulla politica attuale utilizzando la funzione .step() . La politica prevede la probabilità di compiere l’azione scelta in ogni intervallo di tempo.
• Ricevi la ricompensa dall’ambiente in base all’azione dell’agente.
• Accumula le ricompense passo passo e le probabilità logaritmiche delle azioni fino a quando l’agente non raggiunge uno stato terminale.

Il codice qui sotto implementa il passaggio in avanti:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

Utilizzando la retropropagazione e l’ascensione del gradiente per aggiornare la politica

Nella tradizionale apprendimento automatico:

• La perdita si riferisce alla differenza tra l’output previsto e quello reale.
• Minimizzando la perdita usando la discesa del gradiente.

In RL:

• La perdita è un proxy per la quantità su cui l’ottimizzazione del gradiente (o ascesa) deve essere applicata.
• Massimizziamo il ritorno (ricompense cumulative) utilizzando l’ascensione del gradiente.
• Il valore atteso del ritorno è utilizzato come proxy per la perdita nell’ottimizzazione del gradiente. Il valore atteso del ritorno è il prodotto di:
• I ritorni attesi da ciascun passo con
• La probabilità di scegliere l’azione campionata in ciascun passo.
• Per applicare l’ascensione del gradiente utilizzando la retropropagazione, utilizziamo il negativo della perdita.

Il codice qui sotto calcola la perdita:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

Simile agli algoritmi di apprendimento automatico standard, per aggiornare la politica, esegui la retropropagazione rispetto alla funzione di perdita. Il metodo update_policy() qui sotto invoca il metodo calculate_loss(). Poi esegue la retropropagazione su questa perdita per aggiornare i parametri della politica, cioè i pesi del modello della rete di politica.

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

Il ciclo di addestramento

Usiamo le funzioni definite in precedenza per addestrare la policy. Prima di iniziare l’addestramento, abbiamo bisogno:

• Una policy non addestrata inizializzata come un’istanza randomizzata della classe PolicyNetwork.
• Un ottimizzatore che utilizzi l’algoritmo Adam.
• Ipertiparametri per il fattore di sconto, il tasso di apprendimento, il tasso di dropout, la soglia di ricompensa e il numero massimo di epoche di addestramento.

Iteriamo attraverso il ciclo di addestramento fino a quando il ritorno medio supera la soglia di ricompensa. In ogni iterazione, eseguiamo i seguenti passaggi:

• Per ogni episodio, esegui il passaggio in avanti una volta. Raccogli la probabilità logaritmica delle azioni, i ritorni stepwise e il ritorno totale da quell’episodio. Accumula i ritorni episodici in un array.
• Calcola la perdita utilizzando le probabilità logaritmiche e i ritorni stepwise. Esegui la retropropagazione sulla perdita. Utilizza l’ottimizzatore per aggiornare i parametri della policy.
• Controlla se il ritorno medio su N_TRIALS supera la soglia di ricompensa.

Il codice qui sotto implementa questi passaggi:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

Esegui il programma di addestramento chiamando la funzione main():

main()

Questo notebook DataLab contiene l’implementazione sopra del algoritmo del gradiente di policy. Puoi eseguirlo direttamente o usarlo come punto di partenza per modificare l’algoritmo.

Vantaggi e Sfide dei Metodi del Gradiente di Policy

I metodi del gradiente di policy offrono diversi vantaggi, come:

• Gestione degli spazi di azione continui: I metodi basati sul valore (come il Q-learning) sono inefficienti con gli spazi di azione continui perché devono stimare i valori sull’intero spazio di azione. I metodi basati sul gradiente della policy possono ottimizzare direttamente la policy utilizzando il gradiente dei rendimenti attesi. Questo approccio funziona bene con distribuzioni di azioni continue. Pertanto, i metodi basati sul gradiente della policy sono adatti per compiti come il controllo robotico che si basano su spazi di azione continui.
• Politiche stocastiche: I metodi basati sul gradiente della policy possono apprendere politiche stocastiche – che forniscono una probabilità di selezione per ciascuna possibile azione. Ciò consente all’agente di provare una varietà di azioni e riduce il rischio di rimanere bloccati in ottimi locali. Aiuta in ambienti complessi in cui l’agente deve esplorare lo spazio di azione per trovare la policy ottimale. La natura stocastica aiuta a bilanciare l’esplorazione (provare nuove azioni) e lo sfruttamento (scegliere le azioni migliori conosciute), il che è cruciale per gli ambienti con incertezza o ricompense sparse.
• Ottimizzazione diretta della politica : I gradienti della politica ottimizzano direttamente la politica anziché utilizzare le funzioni di valore. Negli spazi di azione continui o ad alta dimensionalità, l’approssimazione dei valori per ogni azione può diventare computazionalmente costosa. Pertanto, i metodi basati sulla politica si comportano bene in tali ambienti. 

Nonostante i loro numerosi vantaggi, i metodi dei gradienti della politica presentano alcune sfide inherent

• Alta varianza nelle stime del gradiente: I metodi del gradiente di politica selezionano azioni campionando una distribuzione di probabilità. In pratica, campionano la traiettoria per stimare il ritorno atteso. Poiché il processo di campionamento è intrinsecamente casuale, i ritorni stimati nelle iterazioni successive possono avere una varianza elevata. Ciò può rendere difficile per l’agente imparare in modo efficiente perché gli aggiornamenti alla politica possono oscillare significativamente tra le iterazioni. 
• Instabilità durante l’addestramento: 
• I metodi del gradiente di politica sono sensibili ad iperparametri come il. Se il tasso di apprendimento è troppo alto, gli aggiornamenti ai parametri della politica possono essere troppo grandi, causando al training di non raggiungere i parametri ottimali. D’altro canto, se il tasso di apprendimento è troppo piccolo, la convergenza può essere lenta. 
• I metodi di policy gradient devono bilanciare esplorazione ed sfruttamento. Se l’agente non esplora abbastanza, potrebbe non raggiungere il vicinato della politica ottimale. Al contrario, se esplora troppo, non convergerà sulla politica ottimale e oscillerà attorno allo spazio azionale.
• Inefficienza del campionamento: I metodi di policy gradient stimano il ritorno seguendo ciascuna politica fino alla terminazione e accumulando le ricompense ad ogni passo. Pertanto, necessitano di molte interazioni con l’ambiente per tracciare un gran numero di traiettorie campionarie. Questo è inefficiente e costoso per ambienti con ampi spazi di stato o azione.

Soluzioni per la stabilità

Poiché l’instabilità è un problema relativamente comune nei metodi di policy gradient, gli sviluppatori hanno adottato varie soluzioni per stabilizzare il processo di formazione. Di seguito, introduciamo soluzioni comuni per stabilizzare l’addestramento utilizzando i gradienti delle politiche:

Utilizzo di funzioni di base

A causa di un campionamento inefficiente, i gradienti dei ritorni stimati durante le iterazioni di addestramento possono avere una grande varianza, rendendo l’addestramento instabile e lento. Un approccio comune per ridurre la varianza è utilizzare funzioni di base, come il metodo Advantage Actor-Critic (A2C). L’idea è utilizzare un proxy (la funzione di vantaggio) anziché il ritorno stimato per la funzione obiettivo.

Il vantaggio viene calcolato come la differenza tra il ritorno effettivo del percorso campionato e il ritorno atteso dato lo stato iniziale. Questo approccio coinvolge l’uso della funzione di valore come valore atteso degli stati e delle coppie stato-azione. Rappresentando la perdita come la differenza tra il ritorno effettivo e il ritorno atteso anziché solamente come i ritorni, A2C riduce la varianza nella funzione di perdita e, di conseguenza, nei gradienti, rendendo l’addestramento più stabile.

Utilizzando la regolarizzazione dell’entropia

In certi ambienti, come quelli con ricompense sparse (solo pochi stati forniscono una ricompensa), la politica adotta rapidamente un approccio deterministico. Adotta anche un approccio avido e sfrutta i percorsi già esplorati. Ciò impedisce ulteriori esplorazioni e spesso porta alla convergenza verso ottimi locali e politiche subottimali.

La soluzione è incoraggiare l’esplorazione riguardo alla penalizzazione della politica quando diventa troppo deterministica. Questo si realizza aggiungendo un termine basato sull’entropia alla funzione obiettivo. L’entropia misura la quantità di casualità nella politica. Maggiore è l’entropia, maggiore è la casualità nelle azioni scelte dall’agente. Questo termine basato sull’entropia è il prodotto del coefficiente di entropia e dell’entropia della politica attuale.

Fare dell’entropia una parte della funzione obiettivo aiuta a raggiungere un equilibrio tra sfruttamento ed esplorazione.

Estensioni del Gradiente di Politica

Tra le varie estensioni dei metodi del gradiente di politica, uno dei più fondamentali è l’algoritmo REINFORCE. Fornisce un’implementazione semplice del teorema del gradiente di politica ed è la base per tecniche più avanzate.

Algoritmo REINFORCE

L’algoritmo REINFORCE, noto anche come Monte Carlo Reinforce, è una delle implementazioni di base del teorema del gradiente della policy. Utilizza metodi Monte Carlo per stimare i rendimenti e i gradienti della policy. Seguendo l’algoritmo REINFORCE, l’agente campiona direttamente tutte le azioni (dallo stato iniziale a quello terminale) dall’ambiente. Questo si contrappone ad altri metodi come TD-Learning e Programmazione Dinamica, che basano le loro azioni sulle stime della funzione di valore.

Di seguito, presentiamo i passaggi di base dell’algoritmo REINFORCE:

• Inizializza la policy con parametri casuali
• Ripeti più episodi di addestramento. Per ciascun episodio:
• Genera ciascun passo dell’intero episodio come segue:
• Passa lo stato alla funzione della policy.
• La funzione di politica genera probabilità per ogni possibile azione.
• Campiona casualmente un’azione da questa distribuzione di probabilità.
• Per ogni stato nell’episodio, stima i ritorni (ricompense cumulative scontate) fino al passo.
• Stima il gradiente della funzione obiettivo (secondo il teorema del gradiente della politica), espresso come prodotto dei ritorni passo dopo passo e delle probabilità di azione per ciascun passo.
• Aggiorna i parametri della politica applicando i gradienti

Per ciascuna politica, è possibile campionare una singola traiettoria per stimare il gradiente (come mostrato sopra) o mediare il gradiente su più traiettorie campionate sotto la stessa politica.

Metodi attore-critico

I metodi attore-critico combinano i metodi del gradiente della politica (come REINFORCE) con le funzioni di valore.

• Il funzionamento dell’attore è simile ai metodi del gradiente della politica. L’attore implementa la politica, selezionando azioni in ciascun passaggio in base alla politica. Aggiorna la politica seguendo il gradiente del rendimento atteso.
• Il critico implementa la funzione di valore, che viene utilizzata come base (discusso nella sezione precedente). Questo aiuta a rendere l’addestramento più efficiente e stabile.

I metodi di policy gradient come REINFORCE stimano i gradienti lungo ogni traiettoria utilizzando il ritorno grezzo. Poiché un processo di campionamento estrae queste traiettorie, può portare a grandi varianze nei ritorni e nei gradienti. Utilizzare una funzione di vantaggio invece dei ritorni grezzi risolve questo problema. La funzione di vantaggio è la differenza tra i ritorni effettivi e quelli attesi (cioè, la funzione di valore). I metodi attore-critico sono una classe di algoritmi. Quando il critico è implementato utilizzando la funzione di vantaggio (l’approccio più comune), viene anche chiamato Advantage actor-critic (A2C).

Ottimizzazione della Politica Prossimale (PPO)

Nei contesti complessi, i metodi attore-critico come A2C da soli non sono sufficienti per controllare la varianza nei ritorni e nei gradienti. In tali casi, limitare artificialmente l’ammontare con cui la politica può cambiare in ogni iterazione aiuta. Questo costringe la politica aggiornata (dopo l’ascensione del gradiente) a trovarsi nel vicinato della vecchia politica.

I metodi come Ottimizzazione della Politica Prossimale apportano due modifiche ai gradienti di politica:

• Usa una funzione di vantaggio. Tipicamente, questa funzione di vantaggio utilizza la funzione di valore come riferimento. In questo senso, sono simili ai metodi A2C. 
• Limita la quantità con cui i parametri della politica possono cambiare in ciascuna iterazione. Questo viene fatto utilizzando una funzione obiettivo surrogata con limitazione. L’algoritmo specifica un intervallo entro il quale il rapporto della nuova politica rispetto alla vecchia politica deve trovarsi. Quando il rapporto (dopo l’aggiornamento del gradiente) supera questi valori predeterminati, viene limitato a trovarsi all’interno dell’intervallo. 

Pertanto, PPO migliora significativamente i metodi di gradiente di politica vanilla, il che migliora la stabilità in ambienti complessi. La funzione obiettivo limitata previene grandi varianze nei ritorni e nei gradienti dal destabilizzare gli aggiornamenti della politica. Per raggiungere un equilibrio tra esplorazione e sfruttamento, è anche possibile modificare PPO per utilizzare la regolarizzazione dell’entropia. Questo viene fatto aggiungendo un termine di entropia (un parametro di scalatura moltiplicato per l’entropia della politica) alla funzione obiettivo.

Recenti progressi

I gradienti di politica sono tra i primi metodi utilizzati per risolvere problemi di RL. Dopo l’avvento di GPU veloci, sono stati proposti vari nuovi approcci per applicare tecniche moderne di ML ai gradienti di politica.

Apprendimento per rinforzo potenziato da gradienti

Negli ultimi anni è stato fatto progresso nell’applicare metodi come il gradient boosting agli algoritmi di RL. Il gradient boosting combina le previsioni di più modelli deboli per generare un singolo modello forte. Questo è indicato come Gradient-Boosted Reinforcement Learning (GBRL). GBRL è un pacchetto Python simile a XGBoost che implementa queste tecniche per gli algoritmi di RL.

Transfer Reinforcement Learning 

Transfer learning (TL) è una tecnica in cui la conoscenza acquisita da un modello viene applicata per migliorare le prestazioni di un altro modello. Il transfer learning è utile perché addestrare modelli di ML da zero è costoso. Gli approcci di TL sono stati utilizzati con gradienti di policy per migliorare le prestazioni dei modelli di RL. Questo approccio è chiamato Transfer Reinforcement Learning (TRL).

Conclusione

I gradienti di politica sono tra gli approcci più fondamentali per risolvere i problemi di RL.

In questo articolo, abbiamo presentato i principi fondamentali dei gradienti di politica e mostrato come derivare il teorema del gradiente di politica. Abbiamo anche dimostrato come implementare un semplice algoritmo basato su gradienti utilizzando PyTorch in un ambiente Gymnasium. Infine, abbiamo discusso delle sfide pratiche e delle estensioni comuni all’algoritmo di gradiente di politica di base.

Se desideri approfondire la tua comprensione dell’apprendimento per rinforzo e dell’apprendimento profondo con PyTorch, dai un’occhiata a questi corsi:

• Corso di Apprendimento per Rinforzo – Impara le basi dell’RL, dai metodi basati sul valore alle tecniche di ottimizzazione della politica.
• Introduzione all’Apprendimento Profondo con PyTorch – Acquisisci esperienza pratica con PyTorch e costruisci modelli di apprendimento profondo da zero.