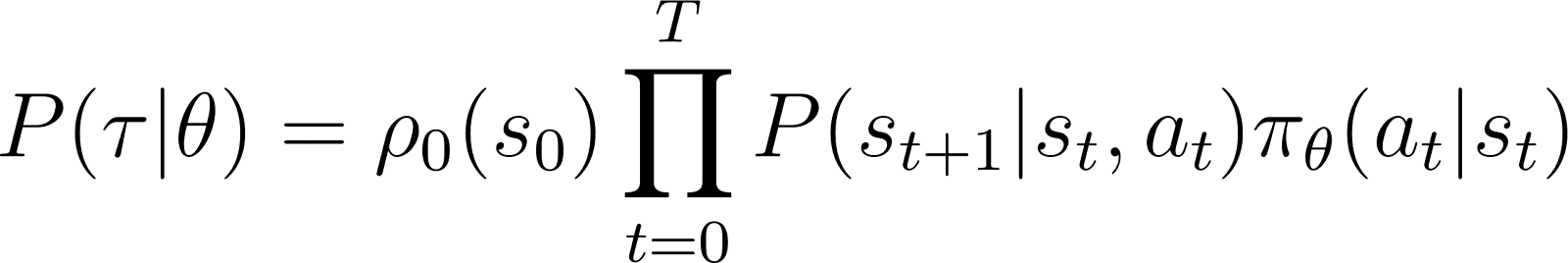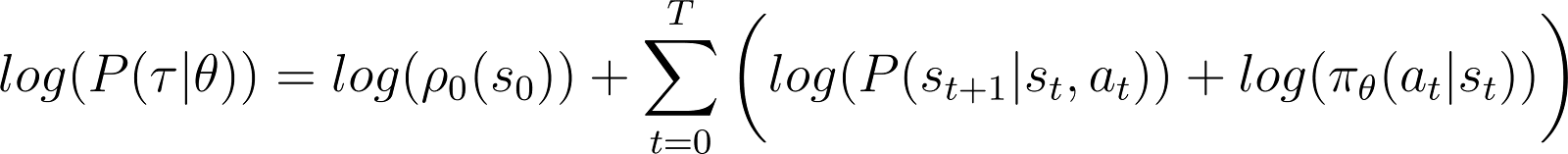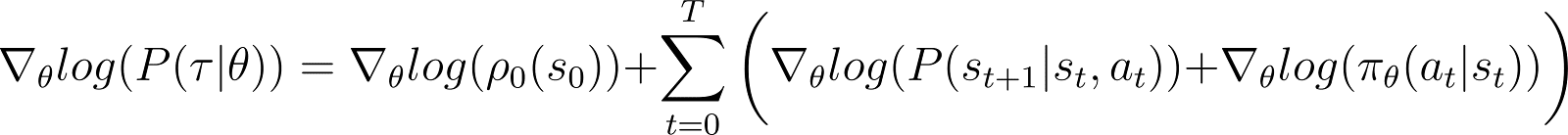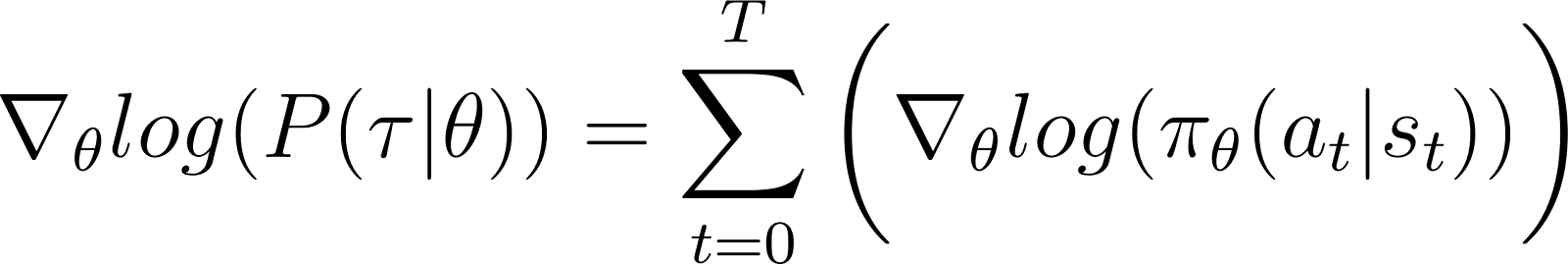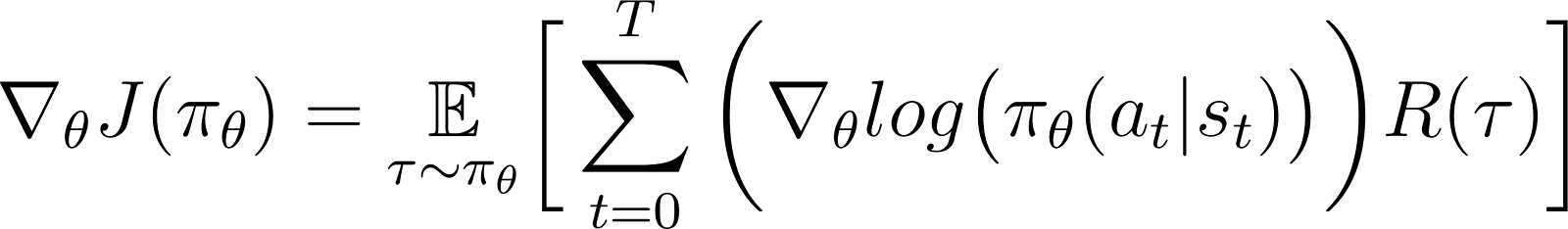Erklärung des Policy-Gradienten-Theorems: Eine praktische Einführung

Warum Policy-Gradient-Methoden verwenden?

Ein wesentlicher Vorteil von Policy-Gradient-Methoden ist ihre Fähigkeit, komplexe Aktionsräume zu handhaben, in denen traditionelle wertbasierte Ansätze Schwierigkeiten haben.

Umgang mit hochdimensionalen Aktionsräumen

Wertbasierte Methoden wie Q-Learning arbeiten, indem sie die Wertefunktion für alle möglichen Aktionen schätzen. Dies wird schwierig, wenn der Aktionsraum der Umgebung entweder kontinuierlich oder diskret, aber groß ist.

Policy-Gradienten-Methoden parametrisieren die Richtlinie und schätzen den Gradienten der kumulativen Belohnungen in Bezug auf die Richtlinienparameter ab. Sie verwenden diesen Gradienten, um die Richtlinie direkt zu optimieren, indem sie ihre Parameter aktualisieren. Daher können sie effizient mit hochdimensionalen oder kontinuierlichen Aktionsräumen umgehen. Policy-Gradienten bilden auch die Grundlage für Methoden des Verstärkungslernens mit menschlichem Feedback (RLHF).

Indem die Richtlinie parametrisiert und ihre Parameter basierend auf Gradienten angepasst werden, können Policy-Gradienten kontinuierliche und hochdimensionale Aktionen effizient handhaben. Dieser direkte Ansatz ermöglicht eine bessere Generalisierung und flexiblere Exploration, was sie für Aufgaben wie die robotergestützte Steuerung und andere komplexe Umgebungen gut geeignet macht.

Das Lernen von stochastischen Richtlinien

Angenommen, es liegt eine Menge von Beobachtungen vor:

• Eine deterministische Richtlinie legt fest, welche Aktion der Agent ausführt.
• Eine stochastische Richtlinie gibt eine Reihe von Aktionen und die Wahrscheinlichkeit an, mit der der Agent jede Aktion wählt.

Bei der Befolgung einer stochastischen Richtlinie kann dieselbe Beobachtung in verschiedenen Iterationen zu verschiedenen Aktionen führen. Dies fördert die Exploration des Aktionsraums und verhindert, dass die Richtlinie in lokalen Optima stecken bleibt. Aus diesem Grund sind stochastische Richtlinien nützlich in Umgebungen, in denen die Exploration entscheidend ist, um den Weg zu maximalen Erträgen zu entdecken.

In Policy-basierten Methoden wird die Richtlinienausgabe in eine Wahrscheinlichkeitsverteilung umgewandelt, wobei jeder möglichen Aktion eine Wahrscheinlichkeit zugewiesen wird. Der Agent wählt eine Aktion, indem er diese Verteilung abtastet, was die Implementierung einer stochastischen Richtlinie ermöglicht. Somit kombinieren Policy-Gradienten-Methoden Exploration mit Ausbeutung, was in Umgebungen mit komplexen Belohnungsstrukturen nützlich ist.

Herleitung des Policy-Gradienten-Theorems

Vor dem Eintauchen in die Ableitung ist es wichtig, die mathematische Notation und die Schlüsselkonzepte festzulegen, die im gesamten Beweis verwendet werden.

Mathematische Notation und Grundlagen

Wie bereits in einem vorherigen Abschnitt erwähnt, besagt der Policy-Gradientensatz, dass die Ableitung des erwarteten Rückgabewerts die Erwartung des Produkts aus der Rückgabe und der Ableitung des Logarithmus des Policies ist.

Bevor wir den Policy-Gradientensatz herleiten, führen wir die Notation ein:

• E[X] bezieht sich auf die probabilistische Erwartung einer Zufallsvariablen X. 
• Mathematisch wird die Richtlinie als Wahrscheinlichkeitsmatrix ausgedrückt, die die Wahrscheinlichkeit der Auswahl verschiedener Aktionen basierend auf verschiedenen Beobachtungen angibt. Eine Richtlinie wird typischerweise als parametrisierte Funktion modelliert, wobei die Parameter als θ dargestellt werden.
• π_θ bezieht sich auf eine Richtlinie, die durch θ parametrisiert ist. In der Praxis handelt es sich bei diesen Parametern um die Gewichte des neuronalen Netzwerks, das die Richtlinie modelliert. 
• Die Trajektorie, τ, bezieht sich auf eine Sequenz von Zuständen, die in der Regel von einem zufälligen Anfangszustand bis zum aktuellen Zeitschritt oder zum Endzustand verläuft.
• ∇_θf bezieht sich auf den Gradienten einer Funktion f bezüglich des Parameters θ.  
• J(π_θ) bezieht sich auf die erwartete Rendite, die der Agent gemäß der Richtlinie π_θ erzielt. Dies ist auch die Zielgröße für den Gradientenaufstieg.
• Die Umgebung belohnt zu jedem Zeitschritt, abhängig von der Aktion des Agenten. Die Rückkehr bezieht sich auf die kumulativen Belohnungen vom Anfangszustand bis zum aktuellen Zeitschritt.
• R(τ) bezieht sich auf die Rendite, die über die Trajektorie τ generiert wird.

Derivationsschritte

Wir zeigen, wie man den Richtliniengradientensatz aus den ersten Prinzipien ableiten und beweisen kann, indem man mit der Expansion der Ziel-Funktion beginnt und den Logarithmus-Derivat-Trick verwendet.

Die Ziel-Funktion (Gleichung 1)

Die Ziel-Funktion in der Richtliniengradientenmethode ist die Rendite.

Ich habe mich angesammelt, indem ich der Trajektorie gemäß der Richtlinie π gefolgt bin, die in Bezug auf Parameter θ ausgedrückt wird. Diese Ziel- oder Zweckfunktion ist gegeben als:

In der obigen Gleichung:

• Die linke Seite (LHS) ist die erwartete Rendite, die durch die Befolgung der Richtlinie π_θ erreicht wird.
• Die rechte Seite (RHS) ist die Erwartung (über die Trajektorie τ , die durch das Befolgen der Richtlinie π_θ in jedem Schritt generiert wird) der Rückkehr R(τ) generiert über die Trajektorie τ.  

Die Ableitung der Zielfunktion (Gleichung 2)

Durch Differentiation (in Bezug auf θ) beider Seiten der obigen Gleichung ergibt:

Der Gradient der Erwartung (Gleichung 3)

Die Erwartung (auf der rechten Seite) kann als Integral über das Produkt von ausgedrückt werden:

• Die Wahrscheinlichkeit, einer Trajektorie τ zu folgen
• Die Renditen, die über die Trajektorie τ

Daher wird die rechte Seite von Gleichung 2 wie folgt neu formuliert:

Der Gradient eines Integrals ist gleich dem Integral des Gradienten. Daher können wir in obigem Ausdruck den Gradienten ∇_θ unter das Integralzeichen bringen. Also wird die rechte Seite zu:

Daher kann Gleichung 2 umgeschrieben werden als:

Die Wahrscheinlichkeit der Trajektorie (Gleichung 4)

Wir werfen nun einen genaueren Blick auf P(τ|θ), die Wahrscheinlichkeit, dass der Agent der Trajektorie τ gemäß den Policy-Parametern θ (und damit der Policy π_θ). Eine Trajektorie besteht aus einer Reihe von Schritten. Daher: 

• Die Wahrscheinlichkeit, die Trajektorie τ zu erhalten, ist das Produkt von:
• Die Wahrscheinlichkeit, alle einzelnen Schritte zu befolgen.

• Im Zeitschritt t wechselt der Agent vom Zustand s zum Zustand s_t+1 durch die Ausführung der Aktion a_t. Die Wahrscheinlichkeit dafür ergibt sich aus dem Produkt von:
• Die Wahrscheinlichkeit, dass die Richtlinie die Aktion vorhersagt a_t im Zustand s_t
• Die Wahrscheinlichkeit, in Zustand st+1 zu gelangen, gegeben die Aktion at und Zustand st ist.

So ergibt sich, ausgehend von einem Anfangszustand s₀ die Wahrscheinlichkeit, dass der Agent die Trajektorie τ basierend auf der Richtlinie π_θ gegeben ist als:

Um es einfacher zu machen, möchten wir das Produkt in der RHS oben als Summe ausdrücken. Also nehmen wir den Logarithmus auf beiden Seiten der obigen Gleichung:

Die Ableitung der Log-Wahrscheinlichkeit (Gleichung 5) 

Wir nehmen nun die Ableitung (in Bezug auf θ) der Log-Wahrscheinlichkeit in der obigen Gleichung. 

Auf der RHS der obigen Gleichung: 

• Der erste Term log ρ₀(s₀) ist konstant in Bezug auf θ. Daher ist seine Ableitung 0. 
• Der erste Term innerhalb der Summe P(s_t+1|s_t, a_t) ist auch unabhängig von θ und seine Ableitung nach θ ist ebenfalls 0. 

Entfernen wir die obigen Nullterme aus der Gleichung, bleiben wir mit (Gleichung 5):

Erinnern wir uns an Gleichung 2:

Gleichung 5 bewertet den Logarithmus des ersten Teils der RHS von Gleichung 2. Wir müssen die Ableitung eines Terms mit seinem Logarithmus in Beziehung setzen. Dies tun wir unter Verwendung der Kettenregel und des Logarithmus-Ableitungstricks.

Der Logarithmus-Ableitungstrick

Wir machen einen Umweg und verwenden die Regeln der Analysis, um ein Ergebnis abzuleiten, das wir verwenden werden, um die vorherige Gleichung zu vereinfachen und für rechnergestützte Methoden geeignet zu machen.

In der Analysis kann die Ableitung eines Logarithmus wie folgt ausgedrückt werden:

Auf diese Weise kann durch Umstellen der obigen Gleichung die Ableitung von x in Bezug auf die Ableitung des Logarithmus von x ausgedrückt werden:

Dies wird manchmal als der Logarithmus-Ableitungstrick bezeichnet.

Die Kettenregel

Gemäß der Kettenregel ist die Ableitung von z(y) nach y, wobei y selbst eine Funktion von θ ist, als:

In diesem Fall, y(θ) steht für P(θ) und z(y) steht für log(y). Somit, 

Anwendung der Kettenregel

Wir wissen aus der Analysis, dass d(log(y)) / dy = 1/y. Verwenden Sie dies im ersten Ausdruck auf der rechten Seite oben. 

Bewegen Sie y auf die linke Seite und verwenden Sie die Notation:

y steht für P(θ). Also ist die obige Gleichung äquivalent zu:

Durch Anwendung des Logarithmus-Differentiations-Tricks

Das obige Ergebnis liefert den ersten Ausdruck auf der rechten Seite von Gleichung 2 (unten gezeigt).

Unter Verwendung des Ergebnisses auf der rechten Seite von Gleichung 2 erhalten wir:

Wir ordnen die Terme unter dem Integral auf der rechten Seite wie folgt um:

Das endgültige Ergebnis ableiten

Beachten Sie, dass der obige Ausdruck die Integralentwicklung einer Erwartung enthält: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

Somit kann die obige RHS als Erwartung ausgedrückt werden:

Wir substituieren die Ableitung der Log-Wahrscheinlichkeit in der Ausdruck der erwarteten Belohnung:

In der obigen Gleichung den Wert von ∇logP(θ) aus Gleichung 5 einsetzen, um zu erhalten:

Dies ist der Ausdruck für den Gradienten der Belohnungsfunktion gemäß dem Policy-Gradienten-Theorem.

Die Intuition hinter dem Policy-Gradient

Policy-Gradient-Methoden wandeln die Ausgabe der Policy in eine Wahrscheinlichkeitsverteilung um. Der Agent zieht eine Stichprobe aus dieser Verteilung, um eine Aktion auszuwählen. Policy-Gradient-Methoden passen die Parameter der Policy an. Dies führt dazu, dass diese Wahrscheinlichkeitsverteilung in jeder Iteration aktualisiert wird. Die aktualisierte Wahrscheinlichkeitsverteilung hat eine höhere Wahrscheinlichkeit, Aktionen auszuwählen, die zu höheren Belohnungen führen.

Der Policy-Gradient-Algorithmus berechnet den Gradienten des erwarteten Ertrags bezüglich der Policy-Parameter. Indem die Policy-Parameter in Richtung dieses Gradienten bewegt werden, erhöht der Agent die Wahrscheinlichkeit, Aktionen auszuwählen, die während des Trainings zu höheren Belohnungen führen.

Im Wesentlichen werden Aktionen, die zu besseren Ergebnissen führten, in Zukunft wahrscheinlicher gewählt, was die Policy schrittweise verbessert, um langfristige Belohnungen zu maximieren.

Implementierung von Policy-Gradients in Python

Nachdem die grundlegenden Prinzipien der Policy-Gradienten diskutiert wurden, zeigen wir, wie man sie mit PyTorch und Gymnasium implementiert.

Erstellung der Umgebung

Als ersten Schritt müssen wir gymnasium und einige unterstützende Bibliotheken wie NumPy und PyTorch installieren.

Zum Installieren von gymnasium und seinen Abhängigkeiten auf einem Server oder lokalen Rechner führen Sie aus:

$ pip install gymnasium 

Zum Installieren in einem Notebook wie Google Colab oder DataLab verwenden Sie:

!pip install gymnasium

Sie importieren diese Pakete innerhalb der Python-Umgebung:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

Codierung eines einfachen Policy-Gradienten-Agenten

Erstellen Sie eine Instanz der Umgebung mit der .make() Methode.

env = gym.make('CartPole-v1')

Wie bei anderen Machine-Learning-Methoden verwenden wir ein neuronales Netzwerk, um den Policy-Gradient-Agenten zu implementieren.

CartPole-v1 ist eine einfache Umgebung, daher entwerfen wir ein einfaches Netzwerk mit 1 versteckten Schicht mit 64 Neuronen. Die Dimension der Eingabeschicht entspricht den Dimensionen des Beobachtungsraums. Die Dimension der Ausgabeschicht entspricht der Größe des Aktionsraums der Umgebung. Somit bildet das Policy-Netzwerk beobachtete Zustände auf Aktionen ab. Bei Eingabe einer Beobachtung gibt das Netzwerk die vorhergesagte Aktion gemäß der Richtlinie aus.

Der folgende Code implementiert das Policy-Netzwerk:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

Training des Agenten

Die Umgebung gibt in jedem Zeitschritt eine Belohnung abhängig vom Zustand und der Aktion des Agenten. Der Policy-Gradient-Ansatz besteht darin, ein Gradientenabstiegsverfahren auf den kumulierten Belohnungen (Return) durchzuführen. Das Ziel ist es, den Gesamtrückkehr zu maximieren.

Um den Rückkehr in einer Episode zu berechnen, addieren Sie (mit einem Diskontierungsfaktor) die Belohnungen aus allen Zeitschritten in dieser Episode. Darüber hinaus ist die Normalisierung der Rückkehr hilfreich, um ein reibungsloses und stabiles Training sicherzustellen. Der folgende Code zeigt, wie dies gemacht wird:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

In jeder Iteration des Vorwärtsdurchgangs führen wir die folgenden Schritte aus:

• Führe den Agenten basierend auf der aktuellen Politik mit der .step() Funktion aus. Die Politik sagt die Wahrscheinlichkeit voraus, die gewählte Aktion in jedem Zeitintervall auszuführen.
• Erhalte die Belohnung von der Umgebung basierend auf der Aktion des Agenten.
• Summiere die schrittweisen Belohnungen und die Log-Wahrscheinlichkeiten der Aktionen, bis der Agent einen Endzustand erreicht.

Der folgende Code implementiert den Vorwärtsdurchgang:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

Verwendung von Rückpropagation und Gradientenanstieg zur Aktualisierung der Politik

In der traditionellen Maschinenlernen:

• Der Verlust bezieht sich auf die Differenz zwischen der vorhergesagten und der tatsächlichen Ausgabe.
• Wir minimieren den Verlust mithilfe des Gradientenabstiegs.

In RL:

• Der Verlust ist ein Platzhalter für die Größe, auf die Gradientenabstieg (oder -anstieg) angewendet werden soll.
• Wir maximieren die Rendite (kumulierte Belohnungen) mit Gradientenaufstieg.
• Der erwartete Renditewert wird als Platzhalter für den Verlust beim Gradientenabstieg verwendet. Der erwartete Renditewert ist das Produkt von:
• Den erwarteten Renditen von jedem Schritt mit
• der Wahrscheinlichkeit, die Aktion in jedem Schritt auszuwählen.
• Um den Gradientenaufstieg mit Rückpropagierung anzuwenden, verwenden wir das Negative des Verlusts.

Der folgende Code berechnet den Verlust:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

Ähnlich wie bei Standard-maschinellen Lernalgorithmen aktualisieren Sie zur Aktualisierung der Richtlinie die Rückpropagierung in Bezug auf die Verlustfunktion. Die Methode update_policy() ruft die Methode calculate_loss() auf. Danach wird Rückpropagierung auf diesen Verlust durchgeführt, um die Richtlinienparameter, d.h. Modellgewichte des Richtliniennetzwerks, zu aktualisieren.

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

Die Trainingsschleife

Wir verwenden die zuvor definierten Funktionen, um das Modell zu trainieren. Bevor wir mit dem Training beginnen, benötigen wir:

• Ein untrainiertes Modell, das als zufällige Instanz der Klasse PolicyNetwork initialisiert ist.
• Einen Optimierer, der den Adam-Algorithmus verwendet.
• Hyperparameter für den Diskontierungsfaktor, Lernrate, Auslassungsrate, Belohnungsschwelle und die maximale Anzahl an Trainingsepochen.

Wir durchlaufen die Trainingsschleife, bis die durchschnittliche Rückkehr die Belohnungsschwelle überschreitet. In jeder Iteration führen wir die folgenden Schritte aus:

• Führen Sie für jede Episode den Vorwärtspass einmal aus. Sammeln Sie die Protokollwahrscheinlichkeit von Aktionen, die schrittweisen Rückgaben und die Gesamtrückgabe aus dieser Episode. Akkumulieren Sie die episodischen Rückgaben in einem Array.
• Berechnen Sie den Verlust unter Verwendung der Protokollwahrscheinlichkeiten und der schrittweisen Rückgaben. Führen Sie die Rückwärtsausbreitung auf dem Verlust aus. Verwenden Sie den Optimierer, um die Richtlinienparameter zu aktualisieren.
• Überprüfen Sie, ob die durchschnittliche Rückkehr über N_TRIALS die Belohnungsschwelle überschreitet.

Der folgende Code implementiert diese Schritte:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

Führen Sie das Schulungsprogramm durch Aufruf der main() Funktion aus:

main()

Dieses DataLab-Arbeitsblatt enthält die obige Implementierung des Policy-Gradient-Algorithmus. Sie können es direkt ausführen oder als Ausgangspunkt für die Modifizierung des Algorithmus verwenden.

Vorteile und Herausforderungen der Policy-Gradient-Methoden

Policy-Gradient-Methoden bieten mehrere Vorteile, wie zum Beispiel:

• Umgang mit kontinuierlichen Aktionsräumen: Wertbasierte Methoden (wie Q-Learning) sind ineffizient bei kontinuierlichen Aktionsräumen, da sie Werte über den gesamten Aktionsraum schätzen müssen. Policy-Gradienten-Methoden können die Richtlinie direkt optimieren, indem sie den Gradienten der erwarteten Renditen verwenden. Dieser Ansatz funktioniert gut mit kontinuierlichen Aktionsverteilungen. Daher sind Policy-Gradienten-Methoden für Aufgaben wie die robotergestützte Steuerung geeignet, die auf kontinuierlichen Aktionsräumen basieren.
• Stochastische Richtlinien: Policy-Gradienten-Methoden können stochastische Richtlinien lernen – die eine Wahrscheinlichkeit für die Auswahl jeder möglichen Aktion angeben. Dies ermöglicht es dem Agenten, eine Vielzahl von Aktionen auszuprobieren und verringert das Risiko, in lokalen Optima stecken zu bleiben. Es hilft in komplexen Umgebungen, in denen der Agent den Aktionsraum erkunden muss, um die optimale Richtlinie zu finden. Die stochastische Natur hilft dabei, die Exploration (das Ausprobieren neuer Aktionen) und die Ausbeutung (das Auswählen der bekannt besten Aktionen) auszubalancieren, was für Umgebungen mit Unsicherheit oder spärlichen Belohnungen entscheidend ist.
• Direkte Richtlinienoptimierung: Richtliniengradienten optimieren die Richtlinie direkt, anstatt Wertefunktionen zu verwenden. In kontinuierlichen oder hochdimensionalen Aktionsräumen kann es rechnerisch aufwendig werden, Werte für jede Aktion zu approximieren. Daher sind richtlinienbasierte Methoden in solchen Umgebungen sehr effektiv. 

Ungeachtet ihrer vielen Vorteile haben Richtliniengradientenmethoden einige inhärente Herausforderungen:

• Hohe Varianz bei Gradientenschätzungen: Policy-Gradienten-Methoden wählen Aktionen durch die Stichprobenauswahl einer Wahrscheinlichkeitsverteilung. Sie sampeln die Trajektorie, um die erwartete Rendite abzuschätzen. Da der Sampelprozess von Natur aus zufällig ist, können die geschätzten Renditen in nachfolgenden Iterationen eine hohe Varianz aufweisen. Dies kann es für den Agenten schwierig machen, effizient zu lernen, da die Aktualisierungen der Richtlinie zwischen den Iterationen erheblich schwanken können.
• Instabilität während des Trainings:
• Policy-Gradienten-Methoden sind empfindlich gegenüber Hyperparametern wie der. Wenn die Lernrate zu hoch ist, können die Aktualisierungen der Richtlinienparameter zu groß sein, was dazu führt, dass das Training die optimalen Parameter verfehlt. Andererseits kann bei einer zu kleinen Lernrate die Konvergenz langsam sein.
• Policy-Gradient-Methoden müssen Exploration und Exploitation ausbalancieren. Wenn der Agent nicht genug erkundet, erreicht er möglicherweise nicht die Nachbarschaft der optimalen Politik. Umgekehrt, wenn er zu viel erkundet, wird er nicht auf die optimale Politik konvergieren und um den Aktionsraum oszillieren.
• Stichprobenineffizienz: Policy-Gradient-Methoden schätzen die Rückkehr, indem sie mit jeder Politik bis zur Beendigung fortfahren und die Belohnungen aus jedem Schritt akkumulieren. Daher benötigen sie viele Interaktionen mit der Umgebung, um eine große Anzahl von Stichprobenbahnen zu ziehen. Dies ist ineffizient und teuer für Umgebungen mit großen Zustands- oder Aktionsräumen.

Lösungen für Stabilität

Da Instabilität ein relativ häufiges Problem bei Policy-Gradient-Methoden ist, haben Entwickler verschiedene Lösungen angenommen, um den Trainingsprozess zu stabilisieren. Im Folgenden stellen wir gängige Lösungen zur Stabilisierung des Trainings mit Policy-Gradients vor:

Verwendung von Basisfunktionen

Aufgrund ineffizienter Stichproben können die Gradienten der während der Trainingsiterationen geschätzten Rückgaben eine hohe Varianz aufweisen, was das Training instabil und langsam macht. Ein gängiger Ansatz zur Reduzierung der Varianz ist die Verwendung von Basisfunktionen, wie zum Beispiel der Advantage Actor-Critic (A2C) Methode. Die Idee besteht darin, anstelle der geschätzten Rückgabe eine Proxy (die Vorteilfunktion) für die Zielfunktion zu verwenden.

Der Vorteil wird als Differenz zwischen der tatsächlichen Rückgabe aus der gesampelten Trajektorie und der erwarteten Rückgabe gegeben dem anfänglichen Zustand berechnet. Dieser Ansatz beinhaltet die Verwendung der Wertfunktion als den erwarteten Wert von Zuständen und Zustand-Aktions-Paaren. Indem der Verlust als Differenz zwischen der tatsächlichen Rückgabe und der erwarteten Rückgabe dargestellt wird, anstatt nur als die Rückgaben selbst, reduziert A2C die Varianz in der Verlustfunktion und damit in den Gradienten, was das Training stabiler macht.

Verwendung von Entropieregularisierung

In bestimmten Umgebungen, wie z.B. in solchen mit spärlichen Belohnungen (nur sehr wenige Zustände geben eine Belohnung), nimmt die Politik schnell einen deterministischen Ansatz an. Sie nimmt auch einen gierigen Ansatz an und nutzt die Pfade, die sie bereits erkundet hat. Dies verhindert weitere Erkundungen und führt oft zu einer Konvergenz zu lokalen Optima und suboptimalen Politiken.

Die Lösung besteht darin, die Erforschung der Bestrafung der Richtlinie zu fördern, wenn sie zu deterministisch wird. Dies wird durch das Hinzufügen eines entropiebasierten Begriffs zur Zielgröße erreicht. Die Entropie misst die Menge an Zufälligkeit in der Richtlinie. Je größer die Entropie, desto mehr Zufälligkeit in den Aktionen, die vom Agenten gewählt werden. Dieser entropiebasierte Begriff ist das Produkt des Entropiekoeffizienten und der Entropie der aktuellen Richtlinie.

Die Einbeziehung der Entropie in die Zielgröße hilft, ein Gleichgewicht zwischen Ausbeutung und Exploration zu erreichen.

Policy Gradient Erweiterungen

Unter den verschiedenen Erweiterungen der Policy-Gradient-Methoden ist einer der grundlegendsten der REINFORCE-Algorithmus. Er bietet eine einfache Implementierung des Policy-Gradient-Theorems und ist die Grundlage für fortgeschrittenere Techniken.

REINFORCE-Algorithmus

Der REINFORCE-Algorithmus, auch bekannt als Monte Carlo Reinforce, ist eine der grundlegenden Implementierungen des Policy-Gradient-Theorems. Er verwendet Monte Carlo-Methoden zur Schätzung von Rückgaben und Richtungsableitungen. Wenn man dem REINFORCE-Algorithmus folgt, sampelt der Agent direkt alle Aktionen (vom Anfangszustand bis zum Endzustand) aus der Umgebung. Dies steht im Gegensatz zu anderen Methoden wie TD-Lernen und dynamischer Programmierung, die ihre Aktionen basierend auf Schätzwerten der Wertefunktion bootstrappen.

Im Folgenden stellen wir die grundlegenden Schritte des REINFORCE-Algorithmus vor:

• Initialisieren der Richtlinie mit zufälligen Parametern
• Wiederholen mehrerer Trainingsfolgen. Für jede Folge:
• Jeden Schritt der gesamten Folge wie folgt generieren:
• Den Zustand an die Richtlinienfunktion übergeben.
• Die Richtlinienfunktion generiert Wahrscheinlichkeiten für jede mögliche Aktion.
• Wählen Sie zufällig eine Aktion aus dieser Wahrscheinlichkeitsverteilung aus.
• Schätzen Sie für jeden Zustand in der Episode die Rückgaben (rabattierte kumulative Belohnungen) bis zum Schritt.
• Schätzen Sie den Gradienten der Ziel-Funktion (gemäß dem Richtliniengradiententheorem), ausgedrückt als das Produkt der schrittweisen Rückgaben und der Aktionswahrscheinlichkeiten für jeden Schritt.
• Aktualisieren Sie die Richtlinienparameter, indem Sie die Gradienten anwenden.

Für jede Richtlinie können Sie eine einzelne Trajektorie beispielhaft auswählen, um den Gradienten abzuschätzen (wie oben gezeigt) oder den Gradienten über mehrere unter derselben Richtlinie ausgewählte Trajektorien durchschnittlich bilden.

Actor-Critic-Methoden

Actor-Critic-Methoden kombinieren Richtliniengradientenmethoden (wie REINFORCE) mit Wertefunktionen.

• Die Arbeitsweise des Schauspielers ähnelt den Richtliniengradientenmethoden. Der Schauspieler implementiert die Richtlinie, indem er in jedem Schritt Aktionen basierend auf der Richtlinie auswählt. Er aktualisiert die Richtlinie, indem er dem Gradienten der erwarteten Rückkehr folgt.
• Der Kritiker implementiert die Wertefunktion, die als Baseline dient (wie im vorherigen Abschnitt erläutert). Dies trägt dazu bei, das Training effizienter und stabiler zu gestalten.

Policy-Gradient-Methoden wie REINFORCE schätzen die Gradienten entlang jeder Trajektorie unter Verwendung des Rohrücklaufs ab. Da ein Abtastvorgang diese Trajektorien zeichnet, kann dies zu großen Varianzen bei den Rückläufen und Gradienten führen. Die Verwendung einer Vorteilsfunktion anstelle der Rohrückläufe löst dieses Problem. Die Vorteilsfunktion ist der Unterschied zwischen den tatsächlichen und erwarteten Rückläufen (d. h. der Wertefunktion). Actor-Critic-Methoden sind eine Klasse von Algorithmen. Wenn der Kritiker unter Verwendung der Vorteilsfunktion implementiert wird (der häufigste Ansatz), wird er auch als Advantage Actor-Critic (A2C) bezeichnet.

Proximal Policy Optimization (PPO)

In komplexen Umgebungen reichen Actor-Critic-Methoden wie A2C allein nicht aus, um die Varianz bei den Rückläufen und Gradienten zu kontrollieren. In solchen Fällen hilft es, künstlich die Menge zu beschränken, um die die Richtlinie in jeder Iteration geändert werden kann. Dies zwingt die aktualisierte Richtlinie (nach dem Gradientenaufstieg), in der Nachbarschaft der alten Richtlinie zu liegen.

Methoden wie Proximal Policy Optimization machen zwei Modifikationen an den Richtliniengradienten:

• Verwenden Sie eine Vorteilsfunktion. In der Regel verwendet diese Vorteilsfunktion die Wertefunktion als Basislinie. In diesem Punkt ähneln sie den A2C-Methoden.
• Beschränken Sie den Betrag, um den sich die Richtlinienparameter in jeder Iteration ändern können. Dies wird mithilfe einer abgeschnittenen Surrogatzielfunktion durchgeführt. Der Algorithmus legt einen Bereich fest, innerhalb dessen das Verhältnis der neuen Richtlinie zur alten Richtlinie liegen muss. Wenn das Verhältnis (nach dem Gradientenupdate) diese vorher festgelegten Werte überschreitet, wird es abgeschnitten, um innerhalb des Bereichs zu liegen.

Damit verbessert PPO die Vanilla-Policy-Gradient-Methoden erheblich, was die Stabilität in komplexen Umgebungen erhöht. Die abgeschnittene Zielfunktion verhindert, dass große Varianzen in den Rückgaben und Gradienten die Politikupdates destabilisieren. Um ein Gleichgewicht zwischen Exploration und Ausbeutung zu erreichen, ist es auch möglich, PPO so zu modifizieren, dass Entropie-Regularisierung verwendet wird. Dies geschieht, indem ein Entropie-Term (ein Skalierungsparameter multipliziert mit der Entropie der Politik) zur Zielfunktion hinzugefügt wird.

Jüngste Fortschritte

Policy-Gradienten gehören zu den frühesten Methoden zur Lösung von RL-Problemen. Nach dem Aufkommen schneller GPUs wurden verschiedene neue Ansätze vorgeschlagen, um moderne ML-Techniken auf Policy-Gradienten anzuwenden.

Gradienten-Boosted Reinforcement Learning

In den letzten Jahren wurden Fortschritte bei der Anwendung von Methoden wie Gradient Boosting auf RL-Algorithmen erzielt. Gradient Boosting kombiniert die Vorhersagen mehrerer schwacher Modelle, um ein einziges starkes Modell zu generieren. Dies wird als Gradient-Boosted Reinforcement Learning (GBRL) bezeichnet. GBRL ist ein Python-Paket ähnlich wie XGBoost, das diese Techniken für RL-Algorithmen implementiert.

Transfer Reinforcement Learning 

Transfer Learning (TL) ist eine Technik, bei der das Wissen, das von einem Modell erworben wurde, angewendet wird, um die Leistung eines anderen Modells zu verbessern. Transfer Learning ist hilfreich, da das Training von ML-Modellen von Grund auf teuer ist. TL-Ansätze wurden mit Policy-Gradients verwendet, um die Leistung von RL-Modellen zu verbessern. Dieser Ansatz wird als Transfer Reinforcement Learning (TRL) bezeichnet.

Fazit

Richtliniengradienten gehören zu den grundlegendsten Ansätzen zur Lösung von RL-Problemen.

In diesem Artikel haben wir die ersten Prinzipien der Richtliniengradienten vorgestellt und gezeigt, wie man den Richtliniengradientensatz herleitet. Wir haben auch demonstriert, wie man einen einfachen auf Gradienten basierenden Algorithmus unter Verwendung von PyTorch in einer Gymnasium-Umgebung implementiert. Abschließend haben wir praktische Herausforderungen und gängige Erweiterungen des grundlegenden Richtliniengradienten-Algorithmus diskutiert.

Wenn Sie Ihr Verständnis für reinforcement learning und deep learning mit PyTorch vertiefen möchten, schauen Sie sich diese Kurse an:

• Reinforcement Learning Track – Lernen Sie die Grundlagen des RL, von wertbasierten Methoden bis hin zu Richtlinienoptimierungstechniken.
• Einführung in Deep Learning mit PyTorch – Sammeln Sie praktische Erfahrungen mit PyTorch und erstellen Sie Deep-Learning-Modelle von Grund auf.