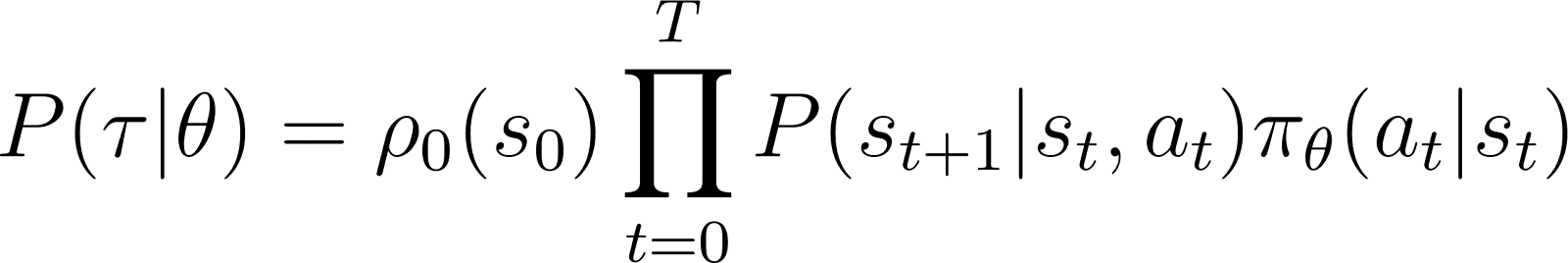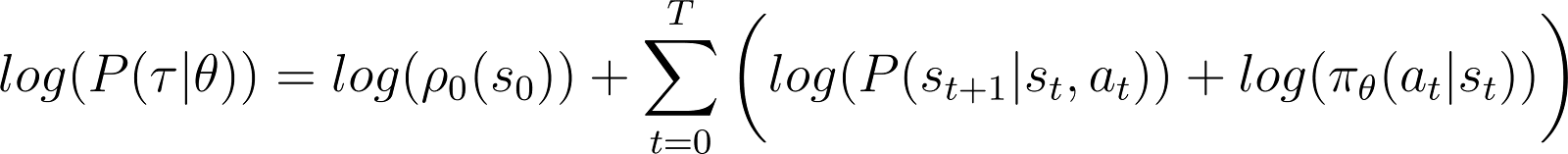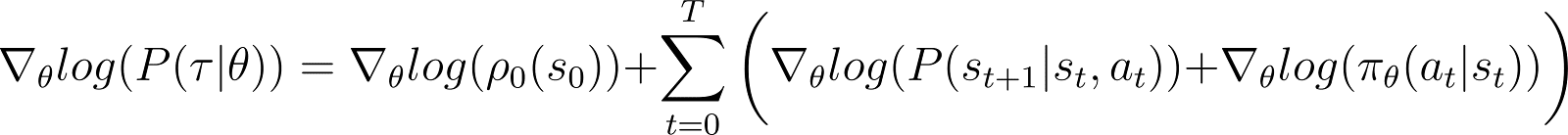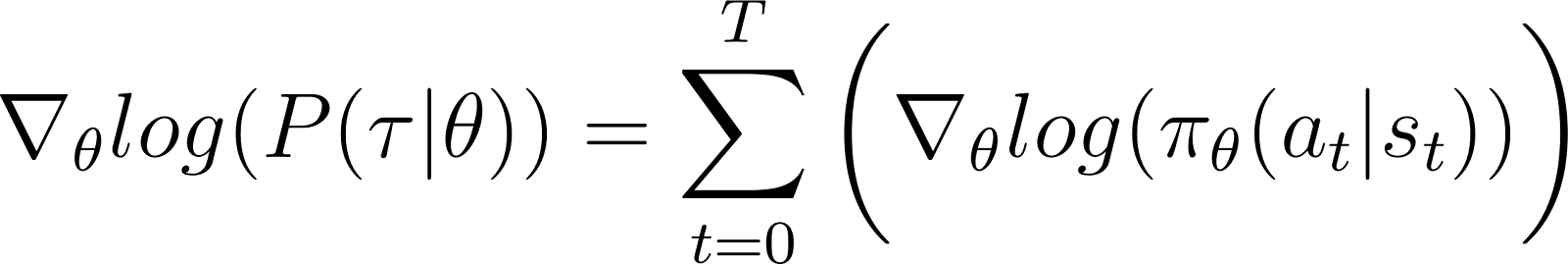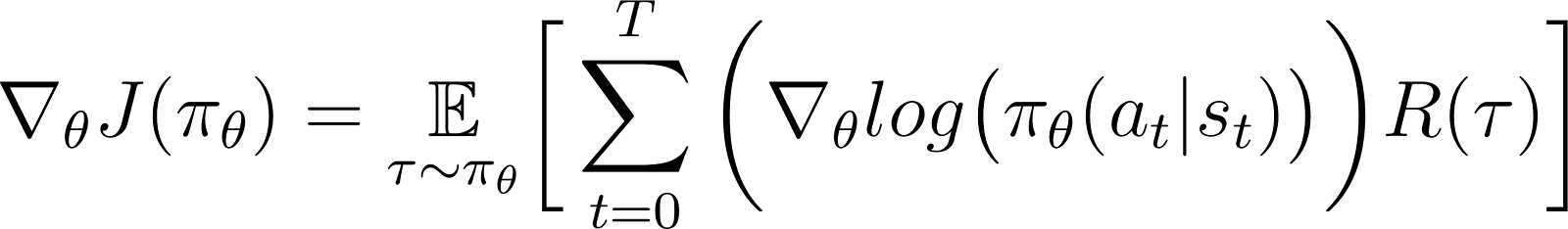משפט הגרדיינט של מדיניות מוסבר: הקדמה מעשית

למה להשתמש בשיטות גרדיאנט מדיניות?

אחת מיתרונות המרכזיים של שיטות גרדיאנט מדיניות היא היכולת שלהן להתמודד עם מרחבי פעולה מורכבים, שבהם גישות מבוססות ערך מסורבלות.

טיפול במרחבי פעולה במימדים גבוהים

שיטות מבוססות ערך, כמו Q-learning, פועלות על ידי הערכת פונקציית הערך עבור כל הפעולות האפשריות. זה הופך לקשה כאשר מרחב הפעולות של הסביבה הוא או רציף או דיסקרטי אך גדול.

שיטות גרדיאנט מדיניות מפרמטרות את המדיניות ומעריכות את הגרדיאנט של הפרסים המצטברים ביחס לפרמטרי המדיניות. הם משתמשים בגרדיאנט הזה כדי למקסם ישירות את המדיניות על ידי עדכון הפרמטרים שלה. לכן, הם יכולים להתמודד ביעילות עם מרחבי פעולה גבוהי מימד או רציפים. גרדיאנטים של מדיניות הם גם הבסיס ל-למידת חיזוק באמצעות משוב אנושי (RLHF) שיטות.

על ידי פרמטריזציה של המדיניות והתאמת הפרמטרים שלה על סמך גרדיאנטים, גרדיאנטים של מדיניות יכולים להתמודד ביעילות עם פעולות רציפות וגבוהות מימד. גישה ישירה זו מאפשרת הכללה טובה יותר וחקר גמיש יותר, מה שהופך אותה למתאימה היטב למשימות כמו שליטה רובוטית וסביבות מורכבות אחרות.

למידת מדיניות סטוכסטית

בהינתן קבוצת תצפיות:

• מדיניות דטרמיניסטית מציינת איזו פעולה הסוכן בוחר.
• מדיניות סטוכסטית מציעה סט של פעולות וההסתברות שהסוכן יבחר בכל פעולה.

בעקבות מדיניות סטוכסטית, אותה תצפיה עשויה להוביל לבחירת פעולות שונות באיטרציות שונות. זה מעודד חקירת המרחב של הפעולה ומונע מהמדיניות להיצמד לאופטימום מקומי. עקב כך, מדיניות סטוכסטית שימושית בסביבות שבהן חקירה היא אופציה חיונית לגילוי הנתיב שמביא להחזרים מקסימליים.

בשיטות המבוססות על מדיניות, פלט המדיניות מומר להפצת ההסתברות, כאשר לכל פעולה אפשרית מוקצתת הסתברות. הסוכן בוחר פעולה על ידי דגימת ההפצה הזו, מה שהופך אפשרי ליישם מדיניות סטוכסטית. כך, שיטות הגרדיינט של מדיניות משלבות חקירה עם פיתוח, שימושיות בסביבות עם מבנים פרסום מורכבים.

הפקת משפט גרדיינט המדיניות

לפני שנצלול לגזירת התיאוריה, חשוב לקבוע את הסימון המתמטי והמושגים המרכזיים המשמשים לאורך ההוכחה.

סימון מתמטי ומבואות

כפי שצוין במקטע קודם, תיאורית גרדיאנט המדיניות קובעת כי הנגזרת של התשואה הצפויה היא הציפייה של מכפלת התשואה והנגזרת של הלוגריתם של המדיניות.

לפני שנגזור את תיאורית גרדיאנט המדיניות, אנו מציגים את הסימון:

• E[X] מתייחס לציפייה הסתברותית של משתנה אקראי X.
• מבחינה מתמטית, המדיניות מבוטאת כמטריצת הסתברויות שמעניקה את ההסתברות לבחירת פעולות שונות בהתבסס על תצפיות שונות. מדיניות בדרך כלל מודלגת כפונקציה פרמטרית, כאשר הפרמטרים מיוצגים כ-θ.
• π_θ מתייחס למדיניות המוגדרת על ידי θ. בפועל, הפרמטרים הללו הם המשקלים של הרשת העצבית שמדמה את המדיניות. 
• המסלול, τ, מתייחס לרצף של מצבים, בדרך כלל מתחיל ממצב ראשוני אקראי עד או עד לזמן הנוכחי או למצב הסופי.
• ∇_θf מתייחס לגרדיאנט של פונקציה f ביחס לפרמטר(ים) θ. 
• J(π_θ) מתייחס לתשואה הצפויה שהושגה על ידי הסוכן בעקבות המדיניות π_θ. זה גם הפונקציה המטרה עבור עלייה גרדיאנטית. 
• הסביבה נותנת פרס בכל שלב זמן, תלוי בפעולת הסוכן. ההחזר הוא התמרת הפרסים הצפויה מהמצב ההתחלתי עד לשלב הנוכחי.
• R(τ) מתייחס להחזר הנוצר מעל המסלול τ.

שלבי ההפקה

אנו מראים כיצד להפיק ולהוכיח את משפט הגרדיאנט מהמדיניות מהעקרונות הראשוניים, התחלה עם הרחבת פונקציית המטרה ושימוש בטריק הלוג-נגזרת.

פונקציית המטרה (משוואה 1)

פונקציית המטרה בשיטת גרדיאנט המדיניות היא ההחזרה

השקפתי כתוצאה מהמסלול שנבחר על פי המדיניות π הביטוי באמצעות הפרמטרים θ. פונקציית המטרה היא: 

במשוואה לעיל:

• הצד שמאל (LHS) מייצג את ההחזר הצפוי שניתן להשיג על ידי עקיפת המדיניות π_θ.
• צד ימין (RHS) הוא הציפייה (על פני המסלול τ שנוצר על ידי מעקב אחרי המדיניות π_θ בכל שלב) של התשואות R(τ) שנוצרו על פני המסלול τ.  

ההבדל של פונקציית המטרה (משוואה 2)

בניפול (נגד θ) שני הצדדים של המשוואה מעלה:

הגרדיינט של הציפיות (משוואה 3)

הציפיות (בצד ימין) ניתן להבעה כאינטגרל על כפל של:

• הסיכוי לעקוב אחר טרקטוריה τ
• ההחזרים שנוצרו במהלך המסלול τ

כך, צד ימין של משוואה 2 מנוסח מחדש כ: 

הגרדיינט של אינטגרל הוא שווה לאינטגרל של הגרדיינט. לכן, בביטוי לעיל, אנו יכולים להעביר את הגרדיינט ∇_θ תחת סימן האינטגרל. לכן, הצד הימני מתהפך להיות:

לכן, משוואה 2 יכולה להיות כתובה מחדש כך:

הסיכוי של המסלול (משוואה 4)

אנו מסתכלים כעת בקרבה על P(τ|θ), הסיכוי של הסוכן לעקוב אחר טרטוריה τ נתונים פרמטרי מדיניות θ (ובכך גם מדיניות π_θ). טרטוריה כוללת סט של שלבים. לכן:

• הסתברות לקבלת טרקטוריה ט היא כפל של:
• ההסתברות של עקבות את כל השלבים האישיים.

• בשלב הזמן t, הסוכן עובר מהמצב s למצב s_t+1 על ידי ביצוע הפעולה a_t. ההסתברות לקריאה זו מתקבלת כמכפלת של:
• הסתברות המדיניות חוזה הזיווג פעולה a_t במצב s_t
• הסיכוי לסיים במצב s_t+1 נתון פעולה a_t ומצב s_t

כך, החל ממצב ראשוני s₀, הסיכוי של הסוכן לעקוב אחרי מסלול τ בהתבסס על מדיניות π_θ ניתנת כ:

כדי לפשט דברים, אנו רוצים לבטא את המוצר בצד ימין של המשוואה למעלה כסכום. לכן, ניקח את הלוגריתם משני הצדדים של המשוואה הנ"ל:

נגזרת הלוגריתם-סיכוי (משוואה 5)

עכשיו ניקח את הנגזרת (לגבי θ) של הלוגריתם סיכוי במשוואה למעלה.

בצד ימין של המשוואה למעלה:

• המונח הראשון לוג ρ₀(s₀) הוא קבוע ביחס ל־θ. לכן הנגזרת שלו היא 0. 
• המונח הראשון בסכימה P(s_t+1|s_t, a_t) גם תלוי תלתות ב- θ והנגזרת שלו לגבי θ היא גם 0.

בהסרת את המונחים מעל לאפס מהמשוואה, נותר לנו (משוואה 5):

זכרו ממשוואה 2 ש:

משוואה 5 מעריכה את הלוגריתם של החלק הראשון של ה-RHS של משוואה 2. אנו צריכים לקשר בין הנגזרת של מונח לבין הלוגריתם שלו. אנו עושים זאת באמצעות כלל השרשרת וטכניקת הלוגריתם-נגזרת.

טכניקת הלוגריתם-נגזרת

אנו עושים עיקוף ומשתמשים בחוקי החשבון הדיפרנציאלי כדי להפיק תוצאה, שתשמש אותנו לפשט את המשוואה הקודמת ולהתאימה לשיטות חישוביות.

בחשבון דיפרנציאלי, הנגזרת של לוגריתם יכולה להיות מבוטאת כך:

לכן, על ידי שינוי סידור המשוואה שלמעלה, הנגזרת של x ניתן לבטא בצורה של הנגזרת של הלוגריתם של x:

מינה היא לפעמים נקראת הטריק של ההפקדה בלוגריתם. 

חוק השרשרת

לפי כלל השרשור, בהנתן z(y) כפונקציה של y, כאשר y עצמו הוא פונקציה של θ, y(θ), הנגזרת של z לגבי θ ניתנת כך:

במקרה הזה, y(θ) מתייחס לP(θ) וz(y) מתייחס לlog(y). לכן,

החילול השרשרתי

אנו יודעים מחשבון שהמפתח של d(log(y)) / dy הוא 1/y. נשתמש בזה בביטוי הראשון של RHS למעלה.

נעביר y ל-LHS ונשתמש ב סימון הבא:

y עומד על P(θ). לכן המשוואה לעיל שקולה ל:

החילוק בשיטת הנגזרת הלוגרתם

התוצאה לעיל נותנת את הביטוי הראשון של צד ימין של משוואה 2 (המוצגת למטה).

באמצעות התוצאה בצד ימין של משוואה 2, נקבל:

אנו מאחדים את המונים תחת האינטגרל בצד ימין כך:

מפענחים את התוצאה הסופית

שימו לב כי הביטוי הנ"ל מכיל את ההרחבה האינטגרלית של ציפייה: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

לכן, ניתן להביע את ה-RHS לעיל כהון:

אנו מחליף את הנגזרת של ההסתברות הלוגרית בביטוי של התגמול המצופה:

במשוואה לעיל, החלף את הערך של ∇logP(θ) ממשוואה 5 כדי לקבל: 

זוהי ההבעה עבור הגרדיאנט של פונקציית התגמול בהתאם לתיאוריית גרדיאנט המדיניות.

האינטואיציה מאחורי גרדיאנט המדיניות

שיטות גרדיאנט המדיניות ממירות את הפלט של המדיניות להפצת הסתברויות. הסוכן מדגם הפצה זו כדי לבחור פעולה. שיטות גרדיאנט המדיניות מתאימות את פרמטרי המדיניות. זה מביא לעדכון הפצת ההסתברויות בכל איטרציה. הפצת ההסתברויות המעודכנת יש סבירות גבוהה יותר לבחור פעולות שמובילות לתגמולים גבוהים יותר.

אלגוריתם גרדיאנט המדיניות מחשב את הגרדיאנט של התשואה הצפויה ביחס לפרמטרי המדיניות. על ידי הזזת פרמטרי המדיניות בכיוון של גרדיאנט זה, הסוכן מגדיל את הסבירות לבחור פעולות שמניבות תגמולים גבוהים יותר במהלך האימון.

בעצם, פעולות שהובילו לתוצאות טובות יותר הופכות ליותר סבירות להיבחר בעתיד, ובכך משפרות בהדרגה את המדיניות למקסום תגמולים לטווח ארוך.

מימוש גרדיאנטים של מדיניות בפייתון

לאחר שדנינו בעקרונות היסוד של הגרדינטי פוליטיקה, אנו מראים כיצד ליישם אותם באמצעות PyTorch ו-Gymnasium.

הגדרת הסביבה

כצעד ראשון, עלינו להתקין gymnasium ומספר ספריות תומכות כמו NumPy ו-PyTorch.

כדי להתקין את gymnasium והתלויותיה בשרת או במחשב מקומי, הריץ:

$ pip install gymnasium 

כדי להתקין באמצעות מחברת כמו Google Colab או DataLab, השתמש:

!pip install gymnasium

אתה מייבא את החבילות הללו בתוך הסביבה של פייתון:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

קידוד של סוכן גרדינטי פוליטיקה

צור מופע של הסביבה באמצעות המתודה .make() .

env = gym.make('CartPole-v1')

כמו במתודולוגיות אחרות של למידת מכונה , אנו משתמשים ברשת עצבית כדי ליישם את סוכן גרדיאנט המדיניות.

CartPole-v1 היא סביבה פשוטה, ולכן אנו מעצבים רשת פשוטה עם שכבת חבויה אחת עם 64 נוירונים. ממדי שכבת הקלט שווים לממדי מרחב התצפיות. ממדי שכבת הפלט שווים לגודל מרחב הפעולות של הסביבה. כך, רשת המדיניות ממפה מצבים שנצפו לפעולות. בהתבסס על תצפית כקלט, הרשת מפיקה את הפעולה הצפויה בהתאם למדיניות.

הקוד למטה מיישם את רשת המדיניות:

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

אימון הסוכן

הסביבה נותנת תגמול בכל צעד בהתאם למצב ולפעולה של הסוכן. הגישה של גרדיאנט המדיניות כוללת הרצת גרדיאנט ירידה על התגמולים המצטברים (החזר). המטרה היא למקסם את ההחזר הכולל.

כדי לחשב את ההחזר בפרק, אתה צובר (עם גורם הנחה) תגמולים מכל הצעדים באותו פרק. בנוסף, נormalizing את ההחזרים מועיל כדי להבטיח אימון חלק ויציב. הקוד למטה מראה כיצד לעשות זאת:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

בכל חזרה של המעבר קדימה, אנו מבצעים את הצעדים הבאים:

• מפעילים את הסוכן על סמך המדיניות הנוכחית באמצעות הפונקציה .step() .המדיניות מנבאת את הסיכוי לבצע את הפעולה הנבחרת בכל שלב זמן.
• מקבלים את העונש מהסביבה על סמך הפעולה של הסוכן.
• מאגדים עונשים לפי שלב ואת לוג הסיכויים של הפעולות עד שהסוכן מגיע למצב סופי.

הקוד למטה מיישם את המעבר קדימה:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

שימוש בהחזרת שגיאות ועלייה של גרדיאנט כדי לעדכן את המדיניות

בלמידת מכונה המסורתית:

• הפסד מתייחס להבדל בין הפלט הניבא לפלט בפועל.
• אנו ממזערים את ההפסד באמצעות ירידת גרדיאנט.

ב-RL:

• ההפסד הוא פונקצית מחליף עבור הכמות עליה ירידת הגרדיאנט (או עלייתו) צריך להיות מיושם.
• אנו מגבירים את ההחזר (הקבלות הצפויות) באמצעות עליית הגרדיאנט.
• ערך ההחזר הצפוי משמש כפונקצית מחליף עבור ירידת הגרדיאנט. ערך ההחזר הצפוי הוא תוצר של:
• ההחזרים הצפויים מכל צעד עם
• הסתברות בחירת הפעולה שנבחרת בכל צעד.
• כדי ליישם עליית גרדיאנט באמצעות backpropagation, אנו משתמשים במינוס של ההפסד.

הקוד למעלה מחשב את ההפסד:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

דומה לאלגוריתמים סטנדרטיים ללמידת מכונה, כדי לעדכן את המדיניות, אתה מריץ backpropagation ביחס לפונקציית ההפסד. שיטת update_policy() למטה מפעילה את השיטה calculate_loss(). לאחר מכן, היא מריצה backpropagation על ההפסד הזה כדי לעדכן את פרמטרי המדיניות, כלומר את משקלי המודל של רשת המדיניות.

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

לולאת האימון

אנחנו משתמשים בפונקציות שהוגדרו קודם לכן כדי לאמן את המדיניות. לפני שמתחילים את האימון, אנחנו צריכים: 

• מדיניות לא מאומנת שהוגדרה כמופע רנדומלי של מחלקת PolicyNetwork. 
• אופטימיזר שמשתמש באלגוריתם אדם. 
• היפרפרמטרים עבור גורם ההנחה, שיעור הלמידה, שיעור הוויתור, סף התגמול, ומספר האפוקים המרבי לאימון. 

אנחנו חוזרים על לולאת האימון עד שהחזרת הממוצע עולה על סף התגמול. בכל חזרה, אנו מבצעים את הצעדים הבאים: 

• לכל פרק, להריץ את המעבר קדימה פעם אחת. לאסוף את ההסתברות הלוגית של הפעולות, את ההחזרות הצעדיות, ואת ההחזר הכולל מהפרק הזה. לצבור את ההחזרות הפרקיות במערך. 
• לחשב את ההפסד באמצעות ההסתברויות הלוגיות וההחזרות הצעדיות. להריץ את ההפצת אחורה על ההפסד. להשתמש באופטימיזר כדי לעדכן את פרמטרי המדיניות. 
• לבדוק אם החזרת הממוצע על פני N_TRIALS עולה על סף התגמול. 

הקוד למטה מממש את הצעדים הללו:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

הפעל את תוכנית האימון על ידי קריאה לפונקציית main():

main()

חוברת עבודה DataLab זו מכילה את המימוש של אלגוריתם המדיניות המתגמלת. ניתן להפעיל אותו ישירות או להשתמש בו כנקודת התחלה לשינוי האלגוריתם.

יתרונות ואתגרים של שיטות מדיניות המתגמלות

שיטות מדיניות המתגמלות מציעות מספר יתרונות, כגון:

• טיפול במרחבי פעולה רציפים: שיטות מבוססות ערך (כמו Q-learning) אינן יעילות עם מרחבי פעולה רציפים מאחר ויש להעריך ערכים על פני כל המרחב הפעולה. שיטות הגרדיינט של מדיניות יכולות לייעל ישירות את המדיניות באמצעות הגרדיינט של התשואות הצפויות. גישה זו עובדת טוב עם חלוקות פעולה רציפות. לכן, שיטות הגרדיינט של מדיניות מתאימות למשימות כמו בקר ברובוטים שמבוססות על מרחבי פעולה רציפים.
• מדיניות סטוכסטית: שיטות הגרדיינט של מדיניות יכולות ללמוד מדיניות סטוכסטית – שנותנת וריאציה של על כל פעולה אפשרית. זה מאפשר לסוכן לנסות מגוון של פעולות ומוריד את הסיכון להתקע באופטימום מקומי. זה עוזר בסביבות מורכבות שבהן הסוכן צריך לחקור את מרחב הפעולה כדי למצוא את המדיניות האופטימלית. הטבע הסטוכסטי עוזר לאיזון בין חקירה (ניסיון של פעולות חדשות) ופיתוח (בחירת הפעולות הידועות ביותר), דבר שקריטי בסביבות עם אי-וודאות או תגמולים רזים.
• אופטימיזציה ישירה של מדיניות: השיטות של מדיניות ממזערות את המדיניות ישירות במקום להשתמש בפונקציות ערך. במרחבי פעולה רציפים או בממדים גבוהים, קרוב לערכי פעולה עשויים להפוך ליקרים חישובית. לכן, שיטות המבוססות על מדיניות מבצעות טוב בסביבות כאלה. 

למרות היתרונות הרבים שלהן, שיטות הגרדיינט של מדיניות נתקלות באתגרים ייחודיים:

• שגיאה גבוהה בהערכות הגרדיאנטים: שיטות גרדיאנט המדיניות בוחרות פעולות על ידי דגימת חלוקת סתירות. בפועל, הן דוגמות את המסלול כדי להעריך את ההחזר הצפוי. מכיוון שתהליך הדגימה הוא אקראי לגמרי, ההחזרים המוערכים באיטרציות לאחר מכן עשויים לכלול שגיאה גבוהה. זה עשוי להקשות על הסוכן ללמוד ביעילות מאחר והעדכונים למדיניות עשויים להתנודד באופן משמעותי בין איטרציות. 
• אי יציבות במהלך האימון: 
• שיטות גרדיאנט המדיניות רגישות להיפרפרמטרים כמו. אם שיעור הלמידה גבוה מדי, העדכונים לפרמטרי המדיניות עשויים להיות גדולים מדי, גורמים לאימון לפספס את הפרמטרים האופטימליים. מצד שני, אם שיעור הלמידה קטן מדי, הספירה עשויה להיות איטית. 
• שיטות גרדיינט פוליטיקה צריכות לא לאזן בין חקירה ופיתוח. אם הסוכן לא חוקר מספיק, ייתכן שהוא לא יגיע לשכונת מדיניות המיטבית. להפך, אם הוא חוקר יתר, הוא לא יגיע למדיניות המיטבית ויתנודד סביב מרחב הפעולה.
• חוסריתות דוגמה: שיטות גרדיינט פוליטיקה מעריכות את ההתחזקות על ידי ביצוע כל מדיניות עד סיום וצבירת הפרסים מכל שלב. לכן, נדרשות המון אינטראקציות עם הסביבה על מנת לצייר מספר גדול של מסלולי דוגמה. זה אינו יעיל ויקר עבור סביבות עם מרחב מצב או פעולה גדול.

פתרונות ליציבות

מאחר שאי-יציבות היא בעיה נפוצה יחסית בשיטות גרדיינט פוליטיקה, מפתחים צירפו פתרונות שונים כדי ליצוב את תהליך האימון. להלן, אנו מציגים פתרונות נפוצים ליציבות האימון באמצעות גרדיינטי פוליטיקה: 

שימוש בפונקציות בסיס.

כתוצאה מדגימה לא יעילה, הגרדיינטים של ההחזרים שמשוערים במהלך אימון עשויים להציג שקיפות גבוהה, מה שיכול לגרום לאימון להיות בלתי יציב ואיטי. גישה נפוצה להפחתת השקיפות היא להשתמש בפונקציות בסיס, כגון שיטת Advantage Actor-Critic (A2C). הרעיון הוא להשתמש בפרוקסי (הפונקציה המרווחת) במקום ההחזר המשוער עבור פונקציית המטרה.

היתרון מחושב כהפרש בין ההחזר האמיתי מהטריה הדוגמתית לבין ההחזר המצופה לפי המצב ההתחלתי. גישה זו כוללת שימוש בפונקציית הערך כערך המצופה של מצבים וזוגות מצב-פעולה. על ידי ייצוג ההפסד כהפרש בין ההחזר האמיתי וההחזר המצופה במקום כהחזרים בלבד, A2C מפחית את השקיפות בפונקציית ההפסד ובגרדיינטים, מה שהופך את האימון ליותר יציב. 

בשימוש ברגולצית אנטרופיה

בסביבות מסוימות, כגון אלה עם שקיפות פעילה נמוכה (רק מעט מאוד מצבים נותנים פרס), המדיניות מסתגלת מהר לגישה דטרמיניסטית. היא גם נוטה לגישה אכזבנית ומנצלת את הנתיבים שכבר חקרה. זה מונע חקירה נוספת ולעתים קרובות מוביל להתכנסות לאופטימום מקומי ולמדיניות חלקאית.

הפתרון הוא לעודד חקירה לגבי הענשת המדיניות כאשר היא הופכת לקבועה מדי. זה מתבצע על ידי הוספת מונח מבוסס אנטרופיה לפונקציית המטרה. האנטרופיה מודדת את כמות האקראיות במדיניות. ככל שהאנטרופיה גדולה יותר, כך יש יותר אקראיות בפעולות שנבחרות על ידי הסוכן. מונח מבוסס אנטרופיה זה הוא התוצר של מקדם האנטרופיה ואנטרופית המדיניות הנוכחית.

הכנסת האנטרופיה לחלק מפונקציית המטרה מסייעת להשיג איזון בין ניצול לחקירה.

הרחבות של גרדיאנט מדיניות

בין הרחבות השונות של שיטות גרדיאנט מדיניות, אחת הבסיסיות ביותר היא האלגוריתם REINFORCE. הוא מספק יישום פשוט של משפט גרדיאנט המדיניות ומהווה את הבסיס לטכניקות מתקדמות יותר.

אלגוריתם REINFORCE

האלגוריתם REINFORCE, ידוע גם בשם Monte Carlo Reinforce, הוא אחד מהמימושים הבסיסיים של משפט הגרדיאנט של מדיניות. הוא משתמש בשיטות Monte Carlo כדי להעריך החזרים וגרדיאנטי מדיניות. כאשר מבצעים את האלגוריתם REINFORCE, הסוכן סוגר כל הפעולות (מהמצב ההתחלתי עד למצב הסופי) ישירות מהסביבה. זה מנגנן בצורה השונה משיטות אחרות כמו למידת TD ותכנות דינמי, שמצמצמות את הפעולות שלהן על סמך הערכים המשוערים של פונקציות הערך.

למטה, אנו מציגים את השלבים הבסיסיים של אלגוריתם REINFORCE:

• אתחול מדיניות עם פרמטרים אקראיים
• חזרה על כמה פרקי אימון. לכל פרק:
• יצירת כל שלב בפרק כולו כך:
• מעבר למצב לפונקציית המדיניות.
• הפונקציית המדיניות יוצרת סיכויים עבור כל פעולה אפשרית.
• לקחו פעולה באופן אקראי מההתפלגות הזו של הסיכויים.
• עבור כל מצב בפרק, הערכו את ההחזרים (קבלת פרסים מורדמים) עד לשלב.
• העריכו את הגרדיאנט של פונקציית המטרה (לפי משפט הגרדיאנט של המדיניות), ביטויו כמכפלת ההחזרים של שלב אחר שלב והסיכויים לפעולה בכל שלב.
• עדכנו את פרמטרי המדיניות על ידי החלת הגרדיאנטים

עבור כל מדיניות, אתה יכול לדגום מסלול בודד כדי להעריך את השיפוע (כפי שמוצג למעלה) או ממוצע את השיפוע על פני מספר מסלולים שנדגמו תחת אותה מדיניות.

שיטות שחקן-מבקר

שיטות שחקן-מבקר משלבות שיטות שיפוע מדיניות (כמו REINFORCE) עם פונקציות ערך.

• עבודת השחקן דומה לשיטות שיפוע מדיניות. השחקן מיישם את המדיניות, בוחר פעולות בכל שלב בהתבסס על המדיניות. הוא מעדכן את המדיניות על ידי מעקב אחר השיפוע של התשואה הצפויה.
• המבקר מיישם את פונקציית הערך, אשר משמשת כבסיס (נדונה בחלק הקודם). זה עוזר להפוך את האימון ליותר יעיל ויציב.

שיטות גרדיאנט מדיניות כמו REINFORCE מעריכות את הגרדיאנטים לאורך כל מסלול תוך שימוש בהחזר הגולמי. מכיוון שתהליך הדגימה שואב את המסלולים הללו, זה יכול להוביל לשונות רבה בהחזרים ובגרדיאנטים. שימוש בפונקציית יתרון במקום בהחזרים הגולמיים פותר את הבעיה הזו. פונקציית היתרון היא ההפרש בין ההחזרים האמיתיים לצפויים (כלומר, פונקציית הערך). שיטות אקטור-קריטיק הן קבוצה של אלגוריתמים. כאשר הקריטיק מיושם באמצעות פונקציית היתרון (הגישה הנפוצה ביותר), הוא נקרא גם אקטור-קריטיק עם יתרון (A2C).

אופטימיזציה של מדיניות פרוקסימלית (PPO)

בסביבות מורכבות, שיטות אקטור-קריטיק כמו A2C לבד לא מספיקות לשלוט בשונות בהחזרים ובגרדיאנטים. במקרים כאלה, הגבלה מלאכותית של כמות השינוי שהמדיניות יכולה לחוות בכל איטרציה עוזרת. זה מאלץ את המדיניות המעודכנת (לאחר עליית הגרדיאנט) להיות בסמוך למדיניות הישנה.

שיטות כמו אופטימיזציה של מדיניות פרוקסימלית עושות שתי התאמות לגרדיאנטים של המדיניות:

• השתמש בפונקציית יתרון . בדרך כלל, פונקציית היתרון הזו משתמשת בפונקציית הערך כבסיס. בכך, הם דומים לשיטות A2C.
• הגבל את הסכום שבו יכולים להשתנות פרמטרי המדיניות בכל איטרציה . זה מתבצע באמצעות פונקציית מטרה חלופית מקוטעת. האלגוריתם מגדיר טווח שבו היחס בין המדיניות החדשה למדיניות הישנה חייב להיות. כאשר היחס (לאחר עדכון גרדיאנט) חורג מהערכים המוקדמים הללו, הוא מקוטע כך שיהיה בטווח.

לכן, PPO משפיעה בצורה משמעותית על שיטות הגרדיינט העליונות של מדיניות ומשפרת את היציבות בסביבות מורכבות. הפונקציה המקוטעת מונעת את השפעתן של וריאנסים גדולים בהחזרים ובגרדיינטים מעדיפים את עדכוני המדיניות. כדי להשיג איזון בין חקירה ופיתוח, ניתן גם לשנות את PPO כך שתשתמש ברגולציה של אנטרופיה. זה נעשה על ידי הוספת מונח אנטרופיה (מקדם כפלי באנטרופיה של המדיניות) לפונקציית המטרה.

התקדמויות אחרונות

גרדיינטי המדיניות הם בין השיטות הראשונות שנעשה בהן שימוש כדי לפתור בעיות של למידת חיזוי. לאחר הגעתם של יחידות עיבוד גרפיות מהירות, הוצעו שיטות חדשות ליישום טכניקות רשתות למידה מודרניות לגרדיינטי המדיניות. 

למידת חיזוי בעזרת הגברת גרדיינטים

בשנים האחרונות, נעשה Fortschritt ביישום שיטות כמו שיפור גרדיאנט על אלגוריתמים של RL. שיפור גרדיאנט משלב את התחזיות ממודלים חלשים מרובים כדי ליצור מודל חזק אחד. זה מכונה למידת חיזוק משופרת על ידי גרדיאנט (GBRL). GBRL הוא חבילת Python דומה לXGBoost שמיישמת את הטכניקות הללו על אלגוריתמים של RL.

למידת חיזוק העברה

למידת העברה (TL) היא טכניקה שבה הידע שהושג על ידי מודל אחד מיושם לשיפור הביצועים של מודל אחר. למידת העברה היא מועילה כי הכשרת מודלים של ML מההתחלה היא יקרה. שיטות TL שימשו עם גרדיאנטים של מדיניות לשיפור הביצועים של מודלים של RL. גישה זו מכונה למידת חיזוק העברה (TRL).

סיכום

גרדיאנטים של מדיניות הם בין הגישות הבסיסיות ביותר לפתרון בעיות RL.

במאמר זה הצגנו את העקרונות הראשוניים של גרדיאנטים של מדיניות והראינו כיצד להניב את משפט הגרדיאנט של המדיניות. כמו כן, הדגמנו כיצד להוציא לפועל אלגוריתם פשוט המבוסס על גרדיאנט באמצעות PyTorch בסביבת Gymnasium. לבסוף, דנו באתגרים מעשיים ותוספות נפוצות לאלגוריתם הבסיסי של גרדיאנט המדיניות.

אם תרצה להעמיק את הבנתך בלמידה מחוזקת ולמידה עמוקה עם PyTorch, בדוק את הקורסים הללו:

• מסלול למידה מחוזקת – למד את היסודות של RL, משיטות מבוססות ערך ועד טכניקות אופטימיזציה של מדיניות.
• מבוא ללמידה עמוקה עם PyTorch – קבל ניסיון מעשי עם PyTorch ובנה מודלים של למידה עמוקה מאפס.