在我長達十年的量化金融之旅中,我遇到過許多統計分佈,但很少有像負二項分佈一樣既有趣的名字又實際有價值。在分析交易模式和風險模型時,我發現儘管負二項分佈看似悲觀,但卻提供了許多較簡單模型無法捕捉的計數過程的洞察。
負二項分佈為建模這些情境提供了複雜的框架,比其較簡單的對應物如泊松分佈更具靈活性。它作為二項分佈的自然延伸,適應需要模擬直到發生一定事件次數的試驗次數,而非在固定次數的試驗中發生的事件次數。
在這份全面指南中,我們將探索負二項分佈的數學基礎、實際應用以及在Python和R中的實現。從基本性質出發,進而探討高級應用,我們將建立對這個強大統計工具的全面理解。
什麼是負二項分佈?
負二項分佈起源於18世紀對於機會遊戲中機率的研究。這種離散機率分佈模擬了在達到一定次數成功之前的一系列獨立伯努利試驗中失敗的次數。每次試驗必須是獨立的且成功的機率相同。
為了直觀地理解這種分佈,可以考慮一個簡單的實驗:不斷面試應聘者直到找到三個合格的人選。該分佈將模擬在找到這三個合格候選人(成功)之前需要多少次失敗的面試。這與二項分佈有根本的不同,後者則模擬了在固定次數試驗中成功的次數,例如在正好20次面試中找到的合格候選人數。
你可以看到,即使名稱“負二項式”可能會讓人感到困惑,但在傳統意義上並不意味著任何負面的東西。 “負面” 一詞源於其歷史推導中涉及負指數。
負二項分佈的應用領域
負二項分佈被應用於許多不同的方式。它應用於金融領域,這是我最常見它的地方,用於模擬像是達到目標利潤水平前的交易日數,或是在找到一定數量符合資格的借款人之前審核信用申請的次數。
更一般地,負二項分佈在建模計數數據時也被證明是有價值的,當變異數超過均值時,這種現象被稱為過度離散。儘管泊松分佈假設均值等於變異數,但現實世界中的計數數據通常表現出更大的變異性。例如,在流行病學中,疾病病例的數量通常變化大於泊松模型預測的範圍,使得負二項分佈更適合於建模疾病傳播。
遺傳學家在分析序列數據時依賴於這種分佈。在RNA序列實驗中,基因表現水平變化很大且變異性高。負二項分佈模型了每個基因映射到的序列讀數,考慮了技術和生物變異。這有助於比假設變異數恆定的方法更準確地識別差異表達的基因。
在生態學研究中,研究人員使用負二項分佈來模擬物種豐富度。以研究鳥類族群為例:某些地區可能有很少的鳥類,而其他地區可能有大量集群,造成比預期更高的變異。負二項分佈有效地模擬這些集群分佈,幫助生態學家了解族群動態並規劃保育工作。
負二項分佈的特性
負二項分佈的特性由兩個關鍵參數決定其形狀和行為。了解這些參數和數學表示有助於我們理解這個分佈如何模擬現實世界的現象。讓我們系統地探索這些特性。
數學表示和參數
負二項分佈具有兩個基本參數:
- r – 目標成功次數(正整數)
- p – 每次試驗成功的機率(介於0和1之間)
這些參數塑造了分佈的行為。考慮追蹤需要進行多少次銷售電話來獲得五個新客戶(r = 5),當每次電話成功的機率為20%(p = 0.2)時。r的值確定了我們的停止點,而p影響了我們可能需要繼續打電話的時間。
當我們增加r但保持p恆定時,分佈會向右移動並變得更分散,反映出我們需要更多次試驗才能取得更多成功。相反,當我們增加p但保持r恆定時,分佈會向左移動並變得更集中,這表明當成功更有可能時,通常需要的試驗次數更少。
概率質量函數(PMF)和累積分佈函數(CDF)
概率质量函数告诉我们在获得r次成功之前需要恰好k次失败的概率。对于负二项分布,PMF为:
其中:
- X代表在获得r次成功之前的失败次数
- (k+r-1 choose k)是二项式系数,表示排列k次失败和r-1次成功的方式数
- p是成功的概率
- r是所需的成功次数
- K是失败次数
例子:在質量控制中,如果我們需要 3 個次品(r = 3),而每個單位有 10% 的次品機會(p = 0.1),我們可以計算特定的概率。例如,在找到第三個次品之前恰好得到 5 個非次品單位(k = 5)的概率是:
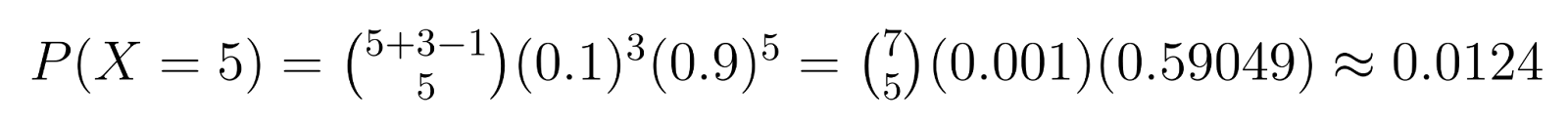
這個計算顯示在找到第三個次品之前恰好需要 5 個非次品單位的概率約為 1.24%。
累積分佈函數(CDF)建立在PMF基礎之上,給我們在達到目標成功數量之前需要 k 或更少失敗的概率:
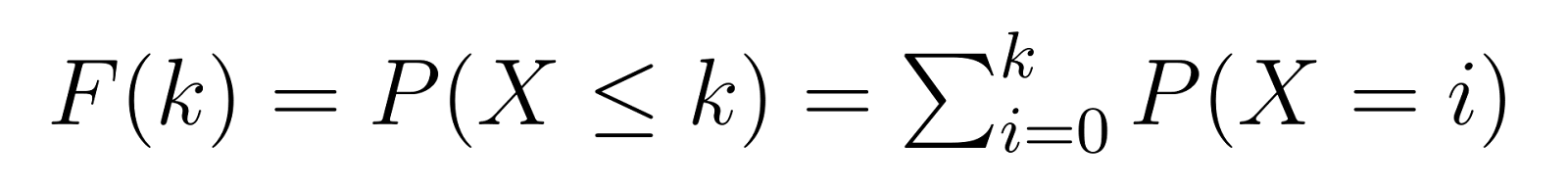
這意味著 F(k) 給出了我們在找到第三個次品之前最多需要 k 個非次品單位的概率。例如,F(5) 將給出我們需要 5 個或更少非次品單位的概率。
均值和方差
負二項分佈的平均值(期望值)和方差具有優雅的公式,揭示了關於平均值(μ)和方差(σ²)的重要性質。
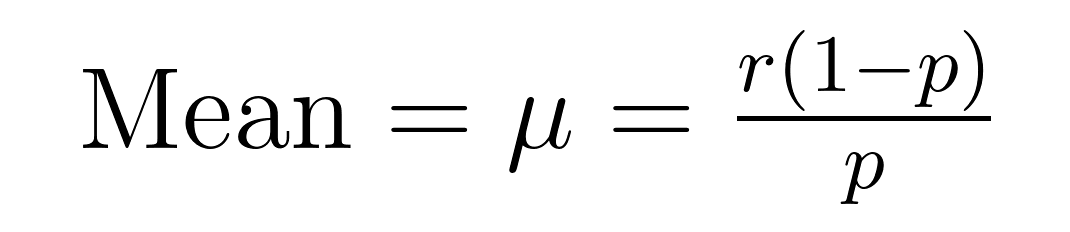
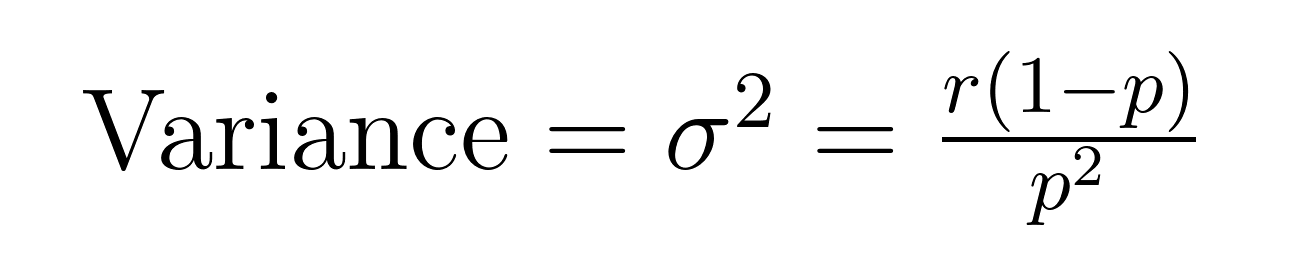
這些公式展示了為什麼這個分佈在建模過度離散數據方面表現出色。請注意,方差始終比平均值大1/p倍。這種內在特性使其自然適用於變異性超過平均值的數據集。
例如,如果我們正在建模客戶服務電話,預期解決5個案例(r = 5),每次嘗試成功率為20%(p = 0.2),則預期的失敗嘗試次數將是:
- 平均值 = 5(1-0.2)/0.2 = 20次失敗
- 方差 = 5(1-0.2)/0.2² = 100
這種較高的變異性解釋了一個現實情況,即有些情況可能會很快解決,而其他情況則需要更多嘗試,這種模式在現實情況中經常被觀察到。
了解這些特性有助於我們識別何時應用負二項分佈,以及如何有效解釋其結果。這些數學基礎為實際應用和實施奠定了基礎,我們將在後續章節中探討。
Python和R中的實施
讓我們驗證之前的例子:計算在找到第三個有缺陷單元之前正好得到5個非缺陷單元的概率(r=3,p=0.1)。
Python實現
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # 計算二項式係數(k+r-1選擇k) binom_coef = math.comb(k + r - 1, k) # 計算p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # 我們的範例參數 k = 5 # 失敗次數(非缺陷單位) r = 3 # 成功次數(缺陷單位) p = 0.1 # 成功機率(缺陷) # 使用我們的函數計算 prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # 使用scipy進行驗證 prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
上述代碼片段應該輸出如下:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R實現
# 計算概率質量函數 k <- 5 # 失敗次數(非缺陷單位) r <- 3 # 成功次數(缺陷單位) p <- 0.1 # 成功機率(缺陷) # 使用dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # 用於驗證的手動計算 manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
上述代碼片段應該輸出與我們的Python示例中相同的數字:
R calculation: 0.0124 Manual Calculation: 0.0124
這兩種實現確認了我們之前計算出的概率大約為0.0124或1.24%。
與其他分佈的關係
了解負二項分佈與其他概率分佈的關係有助於澄清何時應該使用每一個。負二項分佈與統計學中幾個重要分佈有獨特的聯繫。
負二項分佈 vs. 二項分佈
二項分佈是一個基礎起點。當二項分佈計算固定次數試驗中的成功次數時,負二項分佈則通過計算達到固定成功次數所需的試驗次數來翻轉這一概念。這些分佈是互補的 – 如果您需要確切 3 次成功並想知道在確切 8 次試驗中達成這一點的概率,請使用二項分佈。如果您想知道獲得 3 次成功需要確切 8 次試驗的概率,請使用負二項分佈。
負二項分佈與泊松分佈
在建模計數數據時,泊松分佈通常與負二項分佈進行比較。兩者都處理離散事件,但它們在變異數假設上有所不同。泊松分佈的定義特徵是其均值等於其變異數。然而,現實世界的計數數據經常呈現過度離散,即變異數超過均值。負二項分佈自然地容納了這種額外變異性,使其更適合於以下現象:
- 疾病爆發模式,一些病例會導致更多感染
- 顧客投訴數據,其中一些問題觸發多個相關投訴
- 網站流量激增,特定事件導致活動水平升高
負二項分佈 vs. 幾何分佈
當我們設定 r=1 時,幾何分佈出現為負二項分佈的特殊情況,這意味著我們只等待一次成功。這使其非常適合建模以下情景:
- 直到首次成功的嘗試次數
- 可靠性測試中首次失敗的時間
- 研究中首次突破的嘗試次數
負二項分佈作為Gamma-Poisson混合
最終,負二項分佈可以被推導為Gamma-Poisson混合,為其處理過度離散性提供了理論基礎。這種關係有助於解釋為什麼負二項分佈在個體發生率根據Gamma分佈變化的層次模型中運作良好。
優點和限制
負二項分佈提供了獨特的優勢,使其在建模現實世界現象時具有價值,同時也具有數據科學家應考慮的重要限制。
| Advantages | Limitations |
|---|---|
| 當變異數超過平均值時,靈活處理過度離散的數據 | 要求試驗/事件之間獨立 |
| 參數在實際應用中有清晰的解釋 | 在小樣本中,參數估計變得不可靠 |
| 既能容納計數,也能容納比例 | 在計算上比較簡單的分佈更加耗時 |
| 在計數數據中自然地模擬聚類 | 當數據不真正過度離散時,可能會過分擬合 |
| 在時間序列和縱向數據中表現良好 | 假設在試驗中成功的概率是恆定的 |
負二項回歸
負二項回歸將傳統回歸擴展至計數數據,特別是在數據顯示過度離散的情況下。當泊松回歸假設均值等於方差時,負二項回歸放寬了這一約束,使其更適合於現實世界的應用。
考慮一個呼叫中心的情境:我們想要預測每小時的客戶服務電話數量。我們的預測變數可能包括:
- 一天中的時間
- 一週中的天數
- 假日狀態
- 行銷活動狀況
- 天氣條件
標準的泊松回歸可能會低估呼叫量的變異性,特別是在高峰時段或特殊事件期間。負二項式回歸考慮了這種額外的變異性,提供了更現實的預測和置信區間。
結論
通過其能夠建模複雜的計數數據並處理過度離散,負二項分佈仍然是理解和預測現實世界現象的重要工具。正如您所見,它擅長建模過度離散的數據,提供了建模大量不同情景的靈活性,甚至自然延伸到回歸分析。
如果您有興趣加深對機率分佈及其應用的理解,我們的機率與統計課程涵蓋了這些主題的全面內容。我們的課程包括與真實數據集進行的實踐練習,幫助您掌握理論概念和在Python和R中的實際應用。此外,請考慮我們的Python機器學習科學家職業專業。我保證,您將學到很多。
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













