量的ファイナンスを通じての10年間の旅の中で、多くの統計分布に出会いましたが、その中でもネガティブ二項分布ほど興味深い名前でありながら実用的な価値を証明したものは少ないです。取引パターンやリスクモデルを分析する中で、この分布は、その悲観的な名前にもかかわらず、多くのより単純なモデルが捉えられない数え上げプロセスへの洞察を提供してくれることがわかりました。
ネガティブ二項分布は、こうしたシナリオをモデリングするための洗練された枠組みを提供し、ポアソン分布のようなよりシンプルなモデルよりも柔軟性があります。これは、二項分布の自然な拡張であり、一定数のイベントが発生するまでの試行回数をモデル化する必要がある状況に適応します。
この包括的なガイドでは、ネガティブ二項分布の数学的基盤、実用的な応用、そしてPythonとRでの実装について探求します。基本的な特性から始め、高度な応用に移行しながら、この強力な統計ツールについて徹底的に理解していきます。
ネガティブ二項分布とは何ですか?
負の二項分布は、18世紀に偶然のゲームにおける確率の研究を通じて生まれました。この離散確率分布は、あらかじめ決められた成功の数に達するまでの独立した ベルヌーイ試行 のシーケンスにおける失敗の数をモデル化しています。各試行は独立であり、成功の確率は同じでなければなりません。
この分布を直感的に理解するために、シンプルな実験を考えてみましょう:ポジションに適した候補者を見つけるまで候補者にインタビューを行うことです。この分布は、これらの3人の適格な候補者(成功)を見つける前に必要な不成功のインタビュー(失敗)の数をモデル化します。これは、固定された試行回数における成功の数をモデル化する二項分布とは根本的に異なります。例えば、正確に20回のインタビューで見つけた適格な候補者の数などです。
名前が「ネガティブ二項分布」となっているものの、通常の意味での「ネガティブ」を意味するものではありません。この「ネガティブ」の部分は、負の指数を含む歴史的な由来に基づいています。
ネガティブ二項分布の使用領域
ネガティブ二項分布はさまざまな方法で使用されています。私が最も使うのは金融の分野で、そこでは、目標利益水準達成までの取引日数、または特定の数の適格借り手を見つけるまでの審査された信用申請の数などのシナリオをモデル化しています。
一般的に、負の二項分布は、分散が平均値を上回る場合にカウントデータをモデル化する際に有用であることが証明されています。これはオーバーディスパージョンとして知られる現象です。ポアソン分布は平均値と分散が等しいと仮定しますが、実際のカウントデータはしばしばより大きな変動性を示します。たとえば、疫学において、疾病症例の数はしばしばポアソンモデルが予測するよりも変動が大きいため、疾病の拡散をモデル化するには負の二項分布がより適しています。
遺伝学者は、この分布をシーケンスデータを解析する際に利用しています。RNAシーケンシング実験では、遺伝子は高い変動性を持つ異なる発現レベルを示します。負の二項分布は、各遺伝子にマッピングされたシーケンスリードの数をモデル化し、技術的および生物学的な変動の両方を考慮します。これにより、一定の分散を仮定する方法よりも、異なる発現を示す遺伝子をより正確に特定するのに役立ちます。
生態学の研究では、種の豊富さをモデル化するために使用されます。鳥の個体群を研究する場合を考えてみましょう:一部の地域には鳥が少ない一方、他の地域には大きな集団があり、予想よりも分散が大きくなります。ネガティブビノミアルはこれらの集団分布を効果的にモデル化し、生態学者が個体群動態を理解し、保全活動を計画するのに役立ちます。
ネガティブビノミアル分布の特性
ネガティブビノミアル分布は、その形状と挙動を決定する2つの主要なパラメータによって特徴付けられます。これらのパラメータと数学的表現を理解することで、この分布が実世界の現象をどのようにモデル化するかを把握できます。これらの特性を体系的に探ってみましょう。
数学的表現とパラメータ
ネガティブビノミアル分布には2つの基本的なパラメータがあります:
- r – 成功の目標数(正の整数)
- p – 各試行での成功確率(0から1の間)
これらのパラメータは分布の振る舞いを形作ります。例えば、各通話が成功する確率が20%(p = 0.2)で、5人の新規クライアントを獲得するために必要な販売コールの数を追跡する場合(r = 5)。rの値は停止点を決定し、pは通話を続ける期間を左右します。
rを増やしながらpを一定に保つと、分布は右にシフトしてより広がり、より多くの成功を達成するためにより多くの試行が必要であることを反映します。逆に、rを一定に保ちながらpを増やすと、分布は左にシフトしてより集中し、成功確率が高い場合は通常よりも少ない試行が必要であることを示します。
確率質量関数(PMF)と累積分布関数(CDF)
確率質量関数は、成功を達成する前に正確に k 回の失敗が必要な確率を示します。負の二項分布の場合、PMF は次のようになります:
Where:
- X は成功を達成する前の失敗回数を表します
- (k+r-1 choose k) は二項係数で、k 回の失敗と r-1 回の成功を配置する方法の数を表します
- p は成功の確率です
- r は目標の成功回数です
- K は失敗回数です
例:品質管理では、3つの不良品が必要な場合(r = 3)で、各ユニットが不良品である確率が10%(p = 0.1)の場合、特定の確率を計算できます。たとえば、3番目の不良品を見つける前に正確に5つの非不良品を取得する確率は:
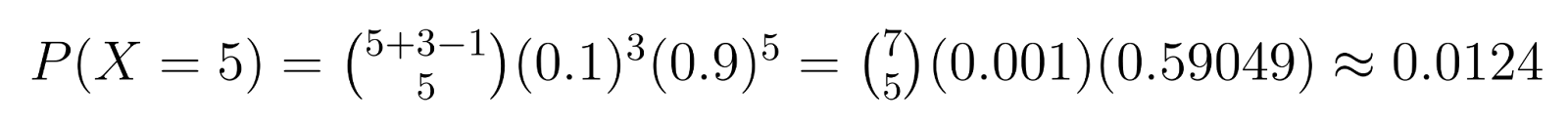
この計算によれば、3番目の不良品を見つける前に正確に5つの非不良品が必要な確率は約1.24%です。
累積分布関数(CDF)は、PMFに基づいており、成功の目標数を達成する前に k 以下の失敗が必要な確率を提供します:
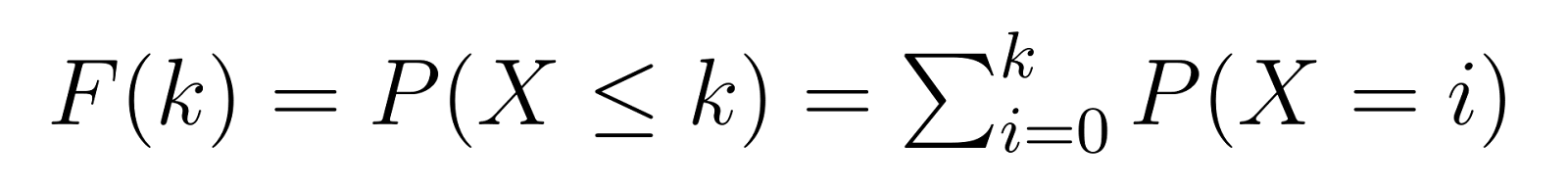
つまり、F(k)は、3番目の不良品を見つける前に最大で k 個の非不良品が必要な確率を示します。たとえば、F(5)は、5個以下の非不良品が必要な確率を示します。
平均と分散
負の二項分布の平均(期待値)と分散には、平均(μ)と分散(σ²)に関する重要な性質を示す優雅な数式があります。
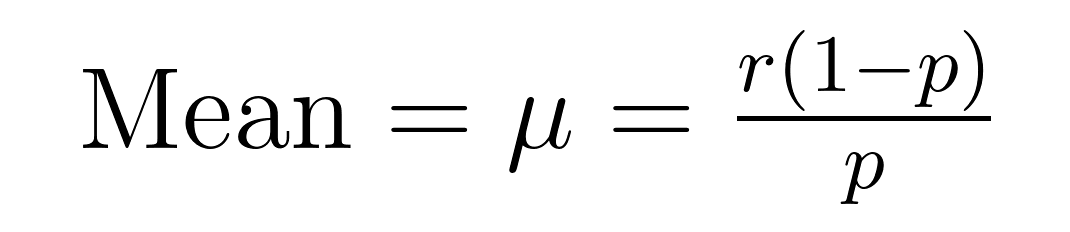
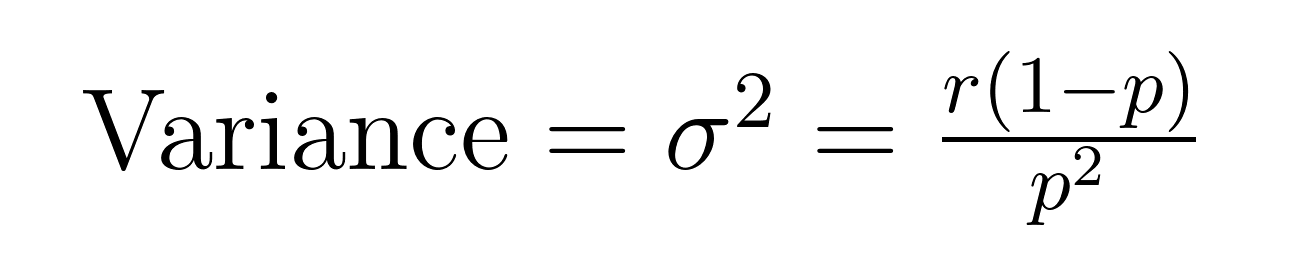
これらの数式により、この分布が過分散データをモデル化するのに優れている理由が示されます。分散が常に平均よりも1/pの因子だけ大きいことに注目してください。この組み込みの性質により、変動が平均値を超えるデータセットに自然に適しています。
たとえば、20%の成功率(p = 0.2)で5件のケース(r = 5)を解決すると予想される顧客サービスの通話をモデル化する場合、失敗した試行の期待数は次の通りです:
- 平均 = 5(1-0.2)/0.2 = 20回の失敗
- 分散 = 5(1-0.2)/0.2² = 100
このより高い分散は、いくつかのケースがすぐに解決される一方、他のケースはより多くの試行が必要とされる現実を反映しています。これは現実のシナリオでよく観察されるパターンです。
これらの特性を理解することで、いつ負の二項分布を適用すべきかを認識し、その結果を効果的に解釈することができます。これらの数学的基礎は、実用的な応用と実装のための舞台を設定し、後続のセクションで探求していきます。
PythonとRにおける実装
前述の例を検証しましょう:3番目の不良品を見つける前にちょうど5つの非不良品を取得する確率を計算する(r=3、p=0.1)。
Pythonの実装
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # バイノミアル係数 (k+r-1 choose k) binom_coef = math.comb(k + r - 1, k) # p^r * (1-p)^k を計算する prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # 例のパラメータ k = 5 # 失敗 (不良品でないユニット) r = 3 # 成功 (不良品ユニット) p = 0.1 # 成功確率 (不良品) # 関数を使って計算する prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # scipy を使って検証する prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
上記のコードスニペットは以下を出力するはずです:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R実装
# 確率質量関数を計算する k <- 5 # 失敗 (不良品でないユニット) r <- 3 # 成功 (不良品ユニット) p <- 0.1 # 成功確率 (不良品) # dnbinom を使用する prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # 検証のための手動計算 manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
上記のコードスニペットは、Pythonの例と同じ数字を出力するはずです。
R calculation: 0.0124 Manual Calculation: 0.0124
両方の実装は、おおよそ0.0124または1.24%という以前に計算した確率を確認しています。
他の分布との関係
負の二項分布が他の確率分布とどのように関連しているかを理解することは、それぞれをいつ使用すべきかを明確にします。負の二項分布は、統計学においていくつかの重要な分布と独自の関係があります。
負の二項分布 vs. 二項分布
二項分布は基本的な出発点として機能します。二項分布は一定の試行回数での成功をカウントしますが、負の二項分布は、一定の成功回数を達成するために必要な試行回数をカウントすることでこの概念を反転させます。これらの分布は補完的です – たとえば正確に3回の成功が必要で、それを8回の試行で達成する確率を知りたい場合は、二項分布を使用します。正確に3回の成功を得るのに8回の試行が必要な確率を知りたい場合は、負の二項分布を使用します。
負の二項分布とポアソン分布
ポアソン分布は、カウントデータをモデル化する際に負の二項分布としばしば比較されます。両者とも離散的なイベントを処理しますが、分散の仮定には違いがあります。ポアソン分布の特徴は、平均が分散と等しいということです。ただし、実際のカウントデータはしばしば過分散が見られ、分散が平均を上回ることがあります。負の二項分布は、この追加の変動性を自然に受け入れるため、次のような現象に適しています:
- 一部の症例が多くの感染を引き起こす疫病の発生パターン
- 顧客からの苦情データで、いくつかの問題が関連する複数の苦情を引き起こす場合
- 特定のイベントが活動レベルを高めることで、ウェブサイトのトラフィックが急増すること
負の二項分布と幾何分布の比較
幾何分布は、r=1に設定することで負の二項分布の特別なケースとして現れます。これは、ただ一度の成功を待っていることを意味します。このため、以下のようなシナリオのモデル化に最適です:
- 最初の成功までの試行回数
- 信頼性テストにおける最初の失敗までの時間
- 研究における最初の突破までの試行回数
負の二項分布はガンマ-ポアソン混合として導出できる
最終的に、負の二項分布はガンマ-ポアソン混合として導出でき、過分散を扱う能力の理論的基盤を提供します。この関係は、個々の発生率がガンマ分布に従って変動する階層モデルで負の二項分布がうまく機能する理由を説明するのに役立ちます。
利点と制限
負の二項分布は、現実の現象をモデル化するために価値のある独自の利点を提供しつつ、データサイエンティストが考慮すべき重要な制限も持っています。
| Advantages | Limitations |
|---|---|
| 分散が平均を超える場合に過分散データを柔軟に処理 | 試行/イベント間に独立性が必要 |
| 実用的な使用のためにパラメータの明確な解釈がある | サンプルが小さいとパラメータ推定が信頼できなくなる |
| カウントと比率の両方を扱える | より単純な分布よりも計算的に集約的 |
| カウントデータのクラスタリングを自然にモデル化 | データが真に過分散でない場合に過剰適合する可能性がある |
| 時系列データや縦断的データでうまく機能する | 試行間で成功の確率が一定であることを仮定 |
ネガティブバイノミアル回帰
ネガティブバイノミアル回帰は、従来の回帰をカウントデータに拡張します。特にデータに過剰分散が見られる場合に適しています。ポアソン回帰が平均と分散が等しいと仮定するのに対し、ネガティブバイノミアル回帰はこの制約を緩和し、実際のアプリケーションにより適したものとなります。
コールセンターのシナリオを考えてみましょう: 私たちは、1時間あたりの顧客サービスコールの数を予測したいと考えています。予測因子には以下が含まれるかもしれません:
- 時間帯
- 曜日
- 祝日ステータス
- マーケティングキャンペーン活動
- 天候条件
通常のポアソン回帰は、ピーク時や特別イベント中に通話量の変動を過小評価する可能性があります。ネガティブ二項回帰はこの追加の変動性を考慮し、より現実的な予測と信頼区間を提供します。
結論
複雑なカウントデータをモデル化し過分散を処理する能力により、ネガティブ二項分布は実世界の現象を理解し予測するための必須ツールとしての地位を保ちます。ご覧の通り、オーバースプレッドされたデータのモデリングに優れており、様々なシナリオを柔軟にモデル化することができ、さらに自然に回帰分析に拡張されます。
確率分布とその応用についての理解を深めたい方には、私たちの 確率と統計のコース をお勧めします。私たちのコースでは、実際のデータセットを使用した実践的な演習が含まれており、理論的な概念とPythonおよびRでの実践的な実装の両方を習得する手助けをします。また、私たちの Pythonでの機械学習科学者のキャリア トラックもぜひご検討ください。きっと多くのことを学べると思います。
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













