במהלך העשור שלי בעולם הפיננסי הכמותי, נתקלתי במספר רב של חלוקות סטטיסטיות, אך מעטן הוכיחו כל כך מעניינות בשם ובערך המעשי כמו ההתפלגות השלילית הבינומיאלית. במהלך ניתוח תבניות סחר ומודלים לניהול סיכונים, גיליתי כי ההתפלגות הזו, למרות השם הפסימי שלה, מציעה תובנות בתהליכי ספירה שמודלים פשוטים רבים נכשלים לקפות.
ההתפלגות השלילית הבינומיאלית מספקת מסגרת מתוחכמת למידול תרחישים כאלה, מציעה גמישות גדולה מאשר המודלים הפשוטים שלה כמו ההתפלגות פואסון. היא משמשת כהרחבה טבעית של ההתפלגות הבינומיאלית, מתאימה למצבים בהם נדרשים למצוא את מספר הניסיונות עד קריאת מספר מסוים של אירועים, במקום המספר של האירועים במספר קבוע של ניסיונות.
במדריך זה, נבחן את היסודות המתמטיים של ההתפלגות השלילית הבינומיאלית, היישומים המעשיים שלה, ואת היישום שלה בפייתון וב-R. נתחיל מהתכונות הבסיסיות ונמשיך ליישומים מתקדמים, נבנה הבנה מעמיקה של הכלי הסטטיסטי הזה ועוצמתו.
מהי התפלגות שלילית בינומיאלית?
ההפצה הבינומיאלית השלילית צמחה במאה ה-18 דרך לימוד ההסתברות במשחקי מזל. הפצת ההסתברות הזו מדגימה את מספר הכישלונות ברצף של ניסויי ברנולי בלתי תלויים לפני השגת מספר מוגדר מראש של הצלחות. כל ניסוי חייב להיות בלתי תלוי ולכלול את אותה הסתברות להצלחה.
כדי להבין את ההפצה הזו באופן אינטואיטיבי, שקול ניסוי פשוט: ראיונות עם מועמדים עד שמוצאים שלושה מתאימים למשרה. ההפצה תדגם את מספר הראיונות הלא מוצלחים (כישלונות) הנדרשים לפני שמוצאים את שלושת המועמדים המתאימים הללו (הצלחות). זה שונה באופן יסודי מההפצה הבינומיאלית, אשר מדגימה במקום זאת את מספר ההצלחות במספר קבוע של ניסויים – כמו מספר המועמדים המתאימים שנמצאו בדיוק ב-20 ראיונות.
כך שניתן לראות, אף על פי שהשם "נגטיבי בינומי" עשוי לעורר תהיות, זה לא מעין כלום שלילי במובן הרגיל. האספקט "נגטיבי" נובע ממקורו ההיסטורי שכולל חזקות שליליות.
השימוש בהפצת הנגטיבית בינומית
ההפצה הנגטיבית בינומית משמשת במגוון רחב של תחומים. היא משמשת בענייני כלכלה, שם אני רואה אותה הכי הרבה, והיא מדמה תרחישים כמו מספר ימי מסחר עד להשגת רווח יעד, או מספר בקשות אשראי שנבדקות לפני מציאת מספר מסוים של לווים מתאימים.
בצורה כללית, ההפצת הבינומיאלית השלילית הוכיחה גם ערך עבור דאטה המודלינג סופרת כאשר השליטה חורגת מהממוצע, תופעה ידועה כעל-פני הפלטר. בעוד שההפצה הפואסונית מניחה כי הממוצע שווה לשליטה, דאטה סופרת ממוצע רבה פעמים מראה משתנות רבה יותר. לדוגמה, באפידמיולוגיה, מספר המקרים של מחלה לעתים תכלית משתנה יותר ממה שמודל פואסון יחזיק, ולכן ההפצה הבינומיאלית השלילית היא יותר מתאימה למודלינג של התפשטות מחלה.
גנטיקאים נועד לסמוך על ההפצה הזו בעת ניתוח דאטה רצפות. בניסויים של רצפי RNA, גנים מראים רמות ביטוי שונות עם וריאציה גבוהה. ההפצה הבינומיאלית מדגימה את מספר רצפים הממופים לכל גן, כשמתחשבת בגירוי טכני וביולוגי. דבר זה עוזר לזהות גנים שנבדלים ביטוי בדיוק יותר מאשר שיטות המניחות שוליות קבועה.
במחקרים אקולוגיים, החוקרים משתמשים בהם כדי ליצור דגמים של שפע מינים. נכיר את המקרה של חקירת אוכלוסיות עופות: באזורים יכול להיות מעט עופות כשבאזורים אחרים יש אשפוז גדול, יוצרים שטחי שטח גבוהים מאשר שציפינו. התפלגות הבינומיאלית השלילית מייצגת באופן יעיל תפקידים אלו, עוזרת לאקולוגים להבין דינמיקת אוכלוסיות ולתכנן מאמצי שימור.
מאפיינים של ההתפלגות הבינומיאלית השלילית
ההתפלגות הבינומיאלית השלילית מאופיינת בשני פרמטרים עיקריים שקובעים את צורתה והתנהגותה. הבנת הפרמטרים הללו והייצוג המתמטי מסייעים לנו להבין איך ההתפלגות הזו מדמה תופעות בעולם האמיתי. בואו נחקור את המאפיינים הללו באופן מערכתי.
ייצוג מתמטי ופרמטרים
ההתפלגות הבינומיאלית השלילית כוללת שני פרמטרים יסודיים:
- r – מספר ההצלחות הרצוי (מספר שלם חיובי)
- p – ההסתברות להצלחה בכל ניסיון (בין 0 ל־1)
הפרמטרים אלו עוצבים איך ההפצה מתנהגת. נפשט לדוגמה את מעקב מספר השיחות למכירה הנדרשות כדי לקבל חמישה לקוחות חדשים (r = 5) כאשר בכל שיחה יש סיכוי של 20% להצלחה (p = 0.2). ערך ה־r קובע את נקודת העצירה שלנו, בעוד ש־p משפיע על כמה זמן אנו יכולים לצפות להמשיך לעשות שיחות.
כאשר אנו מגדילים את ערך r תוך שמירה על p קבוע, ההפצה משתנה לצד ימין והיא מתפשטת יותר, משקפת את הצורך בניסויים נוספים כדי להשיג יותר הצלחות. להפך, כאשר אנו מגדילים את p תוך שמירה על r קבוע, ההפצה משתנה לצד שמאל והיא מתכווצת יותר, מציינת שצפוי להיות צורך בפחות ניסויים כאשר הסיכוי להצלחה גבוה יותר.
פונקציית המסת שקע (PMF) ופונקציית ההפצה הצפופה (CDF)
הפונקציית ההסתברות המוצגת נותנת לנו את ההסתברות לדרוש בדיוק k כישלונות לפני שנצליח להגיע ל-r הצלחות. עבור ההתפלגות הבינומית השלילית, ה-PMF הוא:
Where:
- X מייצג את מספר הכישלונות לפני שמצליחים להשיג r הצלחות
- (k+r-1 בחירה k) הוא מקדם הבינומיאלי, המייצג את מספר הדרכים לסדר k כישלונות ו-r-1 הצלחות
- p היא הסתברות הצלחה
- r הוא מספר ההצלחות הרצוי
- K הוא מספר הכישלונות
דוגמה: בבקרת איכות, אם נצטרך 3 יחידות מושחתות (r = 3) וכל יחידה יש לה 10% סיכוי להיות מושחתת (p = 0.1), אנו יכולים לחשב סיכויים ספציפיים. לדוגמה, הסיכוי לקבל בדיוק 5 יחידות לא מושחתות (k = 5) לפני מציאת היחידה השלישית המושחתת הוא:
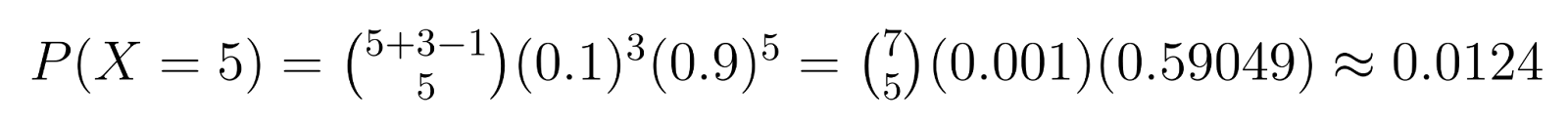
חישוב זה מראה על סיכוי של כ-1.24% לצורך בדיוק 5 יחידות לא מושחתות לפני מציאת היחידה השלישית המושחתת.
פונקציית ההפצה הצטברית (CDF) מבוססת על ה-PMF, נותנת לנו את הסיכוי לדרוש k או פחות כשלות לפני השגת מספר ההצלחות שלנו:
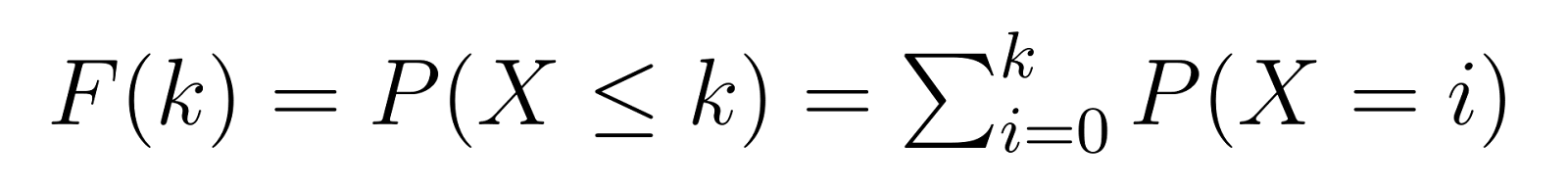
כלומר, F(k) נותנת לנו את הסיכוי לדרוש לכל היותר k יחידות לא מושחתות לפני מציאת היחידה השלישית המושחתת שלנו. לדוגמה, F(5) תקנה לנו את הסיכוי לדרוש 5 או פחות יחידות לא מושחתות.
ממוצע ושטחים
הערך הממוצע והשטח (השונות) של ההתפלגות הבינומית השלילית מכילים נוסחאות אלגנטיות שמגלות מאפיינים חשובים אודות הממוצע (μ) והשטח (σ²).
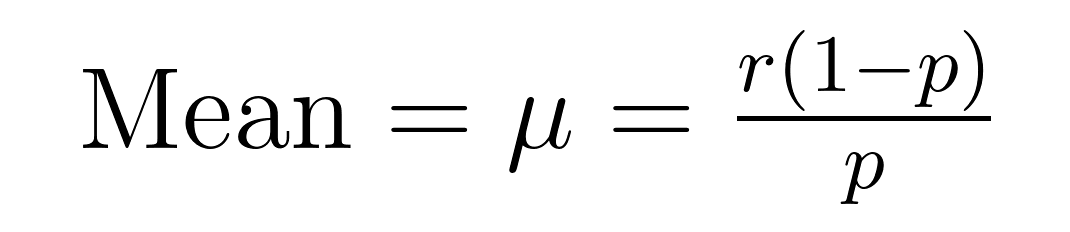
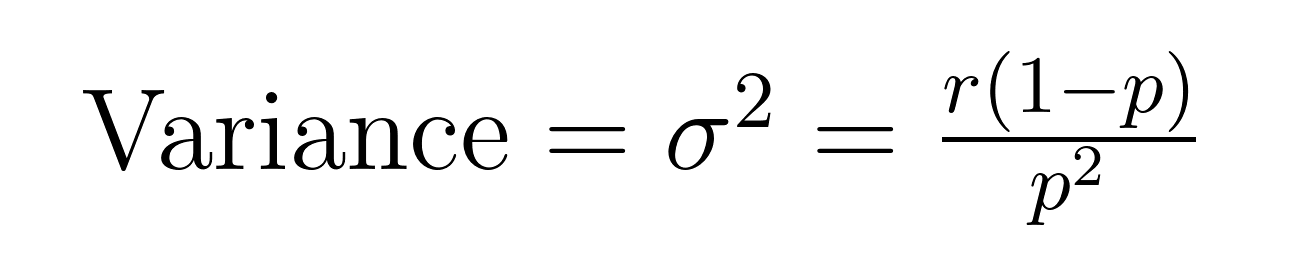
הנוסחאות הללו מדגימות למה ההתפלגות הזו יעילה במודלים של נתונים עם שטח גדול יותר מהממוצע. שימו לב שהשטח תמיד גדול יותר מהממוצע בפרק של 1/p. המאפיין המובנה הזה הופך אותה למתאימה בצורה טבעית למערכות נתונים שבהן השונות חורגת מהערך הממוצע.
לדוגמה, אם אנו מדגימים שיחות לשירות לקוחות שבהן אנו מצפים לפתור 5 מקרים (r = 5) עם שיעור הצלחה של 20% לניסיון (p = 0.2), מספר הניסיונות הנכשלים המצופה הוא:
- ממוצע = 5(1-0.2)/0.2 = 20 כישלונות
- שטח = 5(1-0.2)/0.2² = 100
השונות הגבוהה זו מסבירה את המציאות שיכולה להיות שבמקרים מסוימים ייפתרו במהירות רבה בעוד כאשר מקרים אחרים עשויים לדרוש הרבה יותר ניסיונות, תבנית שנראית לעיתים קרובות בסצנריו האמיתיים.
הבנת המאפיינים הללו מסייעת לנו לזהות מתי להחיל את ההפצה השלילית הבינומיאלית וכיצד לפרש באופן יעיל את תוצאותיה. היסודות המתמטיים אלו מקימים את הבמה ליישומים פרקטיים וליישומים, שנבחן בסעיפים הבאים.
יישום ב־Python ו־R
בואו נאמת את הדוגמה שלנו מהזמן הקודם: חישוב הסתברות לקבלת בדיונית 5 לפני מציאת הבדיקה השלישית (r=3, p=0.1).
יישום Python
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # חישוב מקביל הבינומי (k+r-1 בחר k) binom_coef = math.comb(k + r - 1, k) # חישוב p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # הפרמטרים של הדוגמה שלנו k = 5 # כישלונות (יחידות לא מושחתות) r = 3 # הצלחות (יחידות מושחתות) p = 0.1 # סיכוי להצלחה (מושחתת) # חישוב באמצעות הפונקציה שלנו prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # אימות באמצעות scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
קטע הקוד לעיל צריך להדפיס את הבא:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R implementation
# חישוב פונקציית מסת הסתברות k <- 5 # כישלונות (יחידות לא מושחתות) r <- 3 # הצלחות (יחידות מושחתות) p <- 0.1 # סיכוי להצלחה (מושחתת) # שימוש ב-fnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # חישוב ידני לאימות manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
הקטע הקודם צריך לפלוט את אותם מספרים כמו בדוגמה שלנו בפייתון:
R calculation: 0.0124 Manual Calculation: 0.0124
שתי המימושים מאשרים את ההסתברות שחישבנו מראש בערך של 0.0124 או 1.24%.
קשר להפצויות אחרות
הבנת כיצד ההפצה השלילית הבינומיאלית קשורה להפצויות ההסתברות האחרות עוזרת להבהיר מתי להשתמש בכל אחת מהן. ההפצה השלילית הבינומיאלית יש לה קשרים ייחודיים עם מספר ההפצויות המרכזיים בסטטיסטיקה.
הפצת השלילית הבינומיאלית נגד ההפצה הבינומיאלית
ההפצה הבינומיאלית משמשת כנקודת התחלה היסודית. בעוד ההפצה הבינומיאלית מספרת הצלחות במספר קבוע של ניסויים, ההפצה הבינומיאלית השלילית משנה את הקונספט ומספרת את הניסויים הדרושים למספר קבוע של הצלחות. ההפצות הללו הן תוספות – אם נדרשים בדיוק 3 הצלחות ורוצים לדעת את הסיכוי להשגתן בדיוק ב-8 ניסויים, נשתמש בהפצה בינומיאלית. אם רוצים לדעת את הסיכוי לצורך בדיוק 8 ניסויים להשגת 3 הצלחות, נשתמש בהפצה הבינומיאלית השלילית.
ההפצה הבינומיאלית השלילית נגד ההפצה הפואסונית
ההפצה הפואסונית לעתים קרובות מושווה להפצה הבינומיאלית השלילית במודלים של נתוני ספירה. שתי ההפצות מתמודדות עם אירועים דיסקרטיים, אך הן שונות בהנחות השטח. המאפיין המוגדר של ההפצה הפואסונית הוא שהערך הממוצע שווה לשטח השטח. עם זאת, נתוני ספירה בעולם האמיתי תדיר חורשים פיזור יתר, שבו השטח עולה על הממוצע. ההפצה הבינומיאלית השלילית מתאימה באופן טבעי למידת השטח הנוסף הזה, ובכך מתאימה יותר לתופעות כמו:
- תביעות מחלות שבהן מקרים מסוימים מובילים להידבקויות רבות יותר
- נתוני תלונות של לקוחות שבהן כמה בעיות גורמות למספר תלונות קשורות
- זניקות בתעבורת באתר בהן אירועים מסוימים גורמים לרמות פעילות מורכבות
הפצת בינומית שלילית לעומת הפצת גיאומטרית
ההפצה הגיאומטרית עולה כמקרה מיוחד של ההפצה הבינומית השלילית כאשר אנו מגדירים r=1, המשמע שאנו ממתינים להצלחה אחת בלבד. דבר זה עושה אותה מושלמת לדמות תרחישים כגון:
- מספר הניסיונות עד הצלחה הראשונה
- זמן עד הכשלון הראשון בבדיקת אמינות
- מספר הניסויים עד התקדמות ראשונה במחקר
חלוקת בינומית שלילית כמיקס של גמא-פוisson
לבסוף, ניתן לגזור את החלוקה הבינומית השלילית כמיקס של גמא-פוisson, המספקת בסיס תיאורטי ליכולת שלה להתמודד עם עודף פיזור. קשר זה מסביר מדוע החלוקה הבינומית השלילית פועלת היטב במודלים היררכיים שבהם שיעורי ההתרחשות האישיים משתנים בהתאם לחלוקת גמא.
יתרונות ומגבלות
החלוקה הבינומית השלילית מציעה יתרונות ברורים שהופכים אותה לערך מוסף בתכנון מודלים של תופעות בעולם האמיתי, אך יש לה גם מגבלות חשובות שעל מדעני נתונים לשקול.
| Advantages | Limitations |
|---|---|
| מטפלת בגמישות בנתונים עם פיזור יתר כאשר השונות עולה על הממוצע | דורשת עצמאות בין ניסויים/אירועים |
| פרמטרים בעלי פרשנויות ברורות לשימוש מעשי | אומדן פרמטרים הופך לא אמין עם דגימות קטנות |
| מתאימה גם לספירות וגם לפרופורציות | דרישות חישוביות גבוהות יותר מאשר חלוקות פשוטות |
| מדמה באופן טבעי אשכולות בנתוני ספירה | עלולה להתאים יתר על המידה כאשר הנתונים אינם באמת עם פיזור יתר |
| פועלת היטב עם נתוני סדרות זמן ונתונים לאור זמן | מניחה סיכוי קבוע להצלחה בכל הניסויים |
רגרסיה בינומיאלית שלילית
רגרסיה בינומיאלית שלילית מרחיבה את הרגרסיה המסורתית לנתוני ספירה, במיוחד כאשר הנתונים מראים פיזור יתר. בעוד שרגרסיה פואסונית מניחה שהממוצע שווה לשונות, רגרסיה בינומיאלית שלילית משחררת מגבלה זו, מה שהופך אותה ליותר מתאימה ליישומים בעולם האמיתי.
שקול תרחיש של מרכז שירות לקוחות: אנו רוצים לחזות את מספר שיחות השירות ללקוחות בשעה. המנבאים שלנו עשויים לכלול:
- זמן ביום
- יום בשבוע
- סטטוס חופשה
- פעילות קמפיין שיווקי
- תנאי מזג אוויר
רגרסיה פואסונית סטנדרטית עשויה לתת תחזיות נמוכות לשינוי בנפח השיחות, במיוחד בשעות השיא או באירועים מיוחדים. רגרסיה נגטיבית בינומיאלית מתחשבת בגמישות זו ומספקת תחזיות ומרווחי אמון מותאמים יותר.
מסקנה
בזכות יכולתה לדגם נתוני ספירה מורכבים ולהתמודד עם עודף פיזור, ההתפלגות הנגטיבית הבינומיאלית נשארת ככלי חיוני להבנת ולתחזות פינומנים בעולם האמיתי. כמו שראיתם, היא מצטיינת בדיגום של נתונים עם עודף פיזור, היא נותנת גמישות לדגם מגוון רחב של תרחישים שונים, ואף מרחיבה את תחום הניתוח ברגרסיה באופן טבעי.
אם אתה מעוניין להעמיק את ההבנה שלך בנושאי חלוקות והיישומים שלהן, הקורסים שלנו בסבירות וסטטיסטיקה מציעים כיסוי מקיף של נושאים אלה. הקורסים שלנו כוללים תרגולים מעשיים עם קבוצות נתונים מהעולם האמיתי, שיעזרו לך לשלוט גם במושגים תיאורטיים וגם ביישומים מעשיים ב-Python ו-R. כמו כן, שקול לשקול את מסלול הקריירה שלנו מדען למידת מכונה ב-Python. אני מבטיח, תלמד המון.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













