In mijn tien jaar lange reis door de kwantitatieve financiën, ben ik talloze statistische verdelingen tegengekomen, maar weinigen hebben zich zo intrigerend genoemd en tegelijkertijd praktisch waardevol bewezen als de negatieve binomiale verdeling. Bij het analyseren van handelspatronen en risicomodellen ontdekte ik dat deze verdeling, ondanks zijn ogenschijnlijk pessimistische naam, inzichten biedt in telprocessen die veel eenvoudigere modellen niet kunnen vastleggen.
De negatieve binomiale verdeling biedt een geavanceerd raamwerk voor het modelleren van dergelijke scenario’s, met meer flexibiliteit dan zijn eenvoudigere tegenhangers zoals de Poissonverdeling. Het dient als een natuurlijke uitbreiding van de binomiale verdeling, zich aanpassend aan situaties waarin we het aantal pogingen moeten modelleren totdat een bepaald aantal gebeurtenissen plaatsvindt, in plaats van het aantal gebeurtenissen in een vast aantal pogingen.
In deze uitgebreide gids zullen we de wiskundige grondslagen, praktische toepassingen en implementatie van de negatieve binomiale verdeling in Python en R verkennen. Beginnend bij de basiskenmerken en voortgaand naar geavanceerde toepassingen, zullen we een grondig begrip opbouwen van deze krachtige statistische tool.
Wat is de negatieve binomiale verdeling?
De negatieve binomiale verdeling is ontstaan in de 18e eeuw door de studie van waarschijnlijkheid in kansspelen. Deze discrete waarschijnlijkheidsverdeling modelleert het aantal mislukkingen in een reeks onafhankelijke Bernoulli-experimenten voordat een vooraf bepaald aantal successen wordt behaald. Elke proef moet onafhankelijk zijn en dezelfde kans op succes hebben.
Om deze verdeling intuïtief te begrijpen, stel je een eenvoudig experiment voor: het interviewen van kandidaten totdat er drie gekwalificeerde kandidaten voor een functie zijn gevonden. De verdeling zou het aantal mislukte interviews (mislukkingen) modelleren dat nodig is voordat deze drie gekwalificeerde kandidaten (successen) zijn gevonden. Dit verschilt fundamenteel van de binomiale verdeling, die in plaats daarvan het aantal successen in een vast aantal experimenten modelleert – zoals het aantal gekwalificeerde kandidaten dat precies in 20 interviews wordt gevonden.
Zoals je kunt zien, hoewel de naam “negatieve binomiale” misschien de wenkbrauwen doet fronsen, impliceert het niets negatiefs in de conventionele zin. Het “negatieve” aspect komt voort uit de historische afleiding met betrekking tot negatieve exponenten.
Waar de Negatieve Binomiale Verdeling Wordt Gebruikt
De negatieve binomiale verdeling wordt op veel verschillende manieren gebruikt. Het wordt gebruikt in de financiële sector, waar ik het meest gebruik, waar het scenario’s modelleert zoals het aantal handelsdagen totdat een bepaald winstniveau is bereikt, of het aantal kredietaanvragen dat is beoordeeld voordat een bepaald aantal gekwalificeerde kredietnemers is gevonden.
Meer in het algemeen heeft de negatieve binomiale verdeling ook haar waarde bewezen voor het modelleren van telgegevens wanneer de variantie de gemiddelde waarde overschrijdt, een fenomeen dat bekend staat als overdispersie. Terwijl de Poisson-verdeling ervan uitgaat dat het gemiddelde gelijk is aan de variantie, vertonen telgegevens in de echte wereld vaak meer variabiliteit. Bijvoorbeeld, in de epidemiologie varieert het aantal ziektegevallen vaak meer dan een Poisson-model zou voorspellen, waardoor de negatieve binomiale verdeling meer geschikt is voor het modelleren van ziekteverspreiding.
Genetici vertrouwen op deze verdeling bij het analyseren van sequentiegegevens. In RNA-sequentie-experimenten vertonen genen variërende expressieniveaus met een hoge variabiliteit. De negatieve binomiale verdeling modelleert het aantal sequentiereads dat aan elk gen is toegewezen, rekening houdend met zowel technische als biologische variatie. Dit helpt bij het nauwkeuriger identificeren van genen met differentiële expressie dan methoden die uitgaan van constante variantie.
In ecologische studies gebruiken onderzoekers het om soortenrijkdom te modelleren. Bij het bestuderen van vogelpopulaties: sommige gebieden kunnen weinig vogels hebben terwijl andere grote clusters hebben, wat resulteert in een hogere variantie dan verwacht. De negatieve binomiaal modelleert effectief deze geclusterde verdelingen, waardoor ecologen populatiedynamiek kunnen begrijpen en conserveringsinspanningen kunnen plannen.
Kenmerken van de Negatieve Binomiaal Verdeling
De negatieve binomiaal verdeling wordt gekenmerkt door twee belangrijke parameters die de vorm en het gedrag bepalen. Het begrijpen van deze parameters en de wiskundige representatie helpt ons te begrijpen hoe deze verdeling realistische fenomenen modelleert. Laten we deze kenmerken systematisch verkennen.
Wiskundige representatie en parameters
De negatieve binomiaal verdeling heeft twee fundamentele parameters:
- r – Het gewenste aantal successen (een positief geheel getal)
- p – De kans op succes bij elke poging (tussen 0 en 1)
Deze parameters bepalen hoe de verdeling zich gedraagt. Overweeg het bijhouden van het aantal verkoopgesprekken dat nodig is om vijf nieuwe klanten binnen te halen (r = 5) wanneer elke oproep een kans van 20% op succes heeft (p = 0,2). De waarde van r bepaalt ons stoppunt, terwijl p invloed heeft op hoelang we verwachten oproepen te blijven maken.
Als we r verhogen terwijl we p constant houden, verschuift de verdeling naar rechts en wordt meer verspreid, wat aangeeft dat we meer pogingen nodig hebben om meer successen te behalen. Daarentegen verschuift de verdeling naar links en wordt meer geconcentreerd wanneer we p verhogen terwijl we r constant houden, wat aangeeft dat er doorgaans minder pogingen nodig zijn wanneer succes waarschijnlijker is.
Kansmassafunctie (PMF) en cumulatieve verdelingsfunctie (CDF)
De kansmassafunctie geeft ons de kans op precies k mislukkingen voordat we r successen behalen. Voor de negatieve binomiale verdeling is de KMF:
Waar:
- X het aantal mislukkingen voor het behalen van r successen vertegenwoordigt
- (k+r-1 kiezen k) is de binomiaalcoëfficiënt, die het aantal manieren vertegenwoordigt om k mislukkingen en r-1 successen te rangschikken
- p is de kans op succes
- r is het gewenste aantal successen
- K is het aantal mislukkingen
Voorbeeld: Bij kwaliteitscontrole, als we 3 defecte eenheden nodig hebben (r = 3) en elke eenheid een kans van 10% heeft om defect te zijn (p = 0.1), kunnen we specifieke waarschijnlijkheden berekenen. Bijvoorbeeld, de waarschijnlijkheid om precies 5 niet-defecte eenheden (k = 5) te krijgen voordat we de derde defecte vinden is:
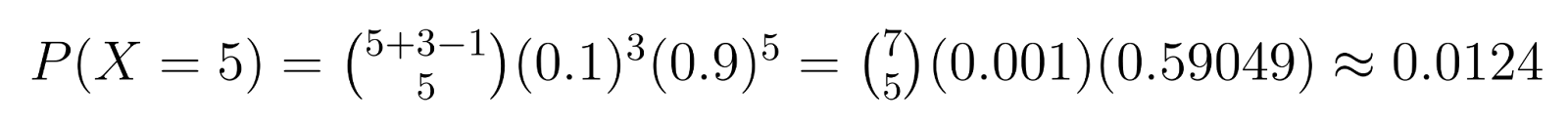
Deze berekening toont een kans van ongeveer 1,24% om precies 5 niet-defecte eenheden nodig te hebben voordat we de derde defecte vinden.
De cumulatieve verdelingsfunctie (CDF) bouwt voort op de PMF en geeft ons de kans om k of minder mislukkingen nodig te hebben voordat we ons streefaantal successen bereiken:
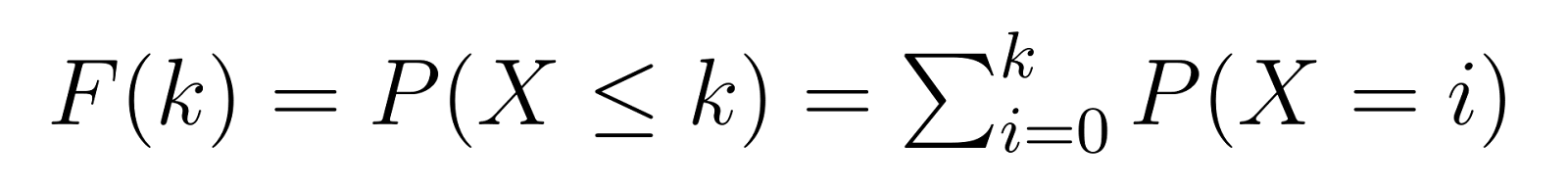
Dit betekent dat F(k) ons de kans geeft om hoogstens k niet-defecte eenheden nodig te hebben voordat we onze derde defecte vinden. Bijvoorbeeld, F(5) zou ons de kans geven om 5 of minder niet-defecte eenheden nodig te hebben.
Gemiddelde en variantie
De verwachtingswaarde en variantie van de negatieve binomiale verdeling hebben elegante formules die belangrijke eigenschappen over de verwachtingswaarde (μ) en variantie (σ²) onthullen.
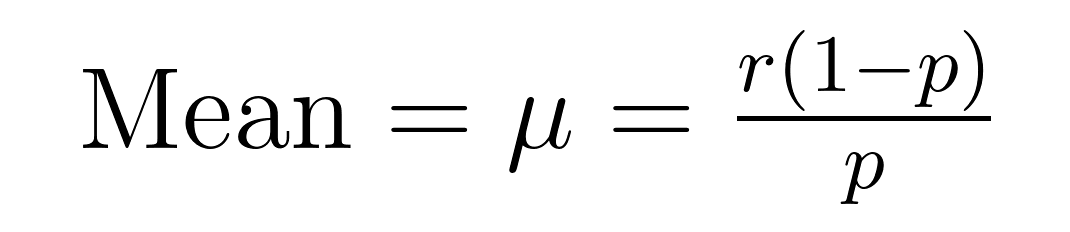
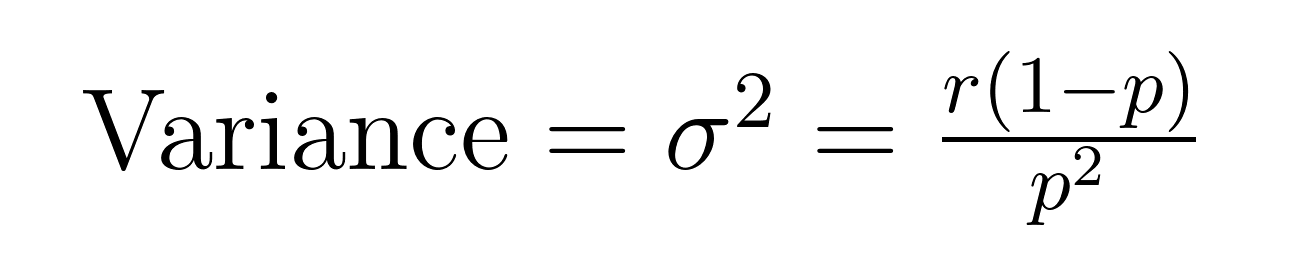
Deze formules tonen waarom deze verdeling uitblinkt in het modelleren van overmatig verdeelde gegevens. Let op dat de variantie altijd groter is dan de verwachtingswaarde met een factor van 1/p. Deze ingebouwde eigenschap maakt het van nature geschikt voor datasets waar de variabiliteit de gemiddelde waarde overschrijdt.
Bijvoorbeeld, als we klantenservicegesprekken modelleren waarbij we verwachten 5 gevallen op te lossen (r = 5) met een succespercentage van 20% per poging (p = 0.2), zou het verwachte aantal mislukte pogingen zijn:
- Verwachtingswaarde = 5(1-0.2)/0.2 = 20 mislukkingen
- Variantie = 5(1-0.2)/0.2² = 100
Deze hogere variantie houdt rekening met de realiteit dat sommige gevallen snel kunnen worden opgelost, terwijl andere veel meer pogingen vereisen, een patroon dat vaak wordt waargenomen in echte scenario’s.
Het begrijpen van deze kenmerken helpt ons te herkennen wanneer we de negatieve binomiale verdeling moeten toepassen en hoe we de resultaten effectief kunnen interpreteren. Deze wiskundige fundamenten leggen de basis voor praktische toepassingen en implementatie, die we in de volgende secties zullen verkennen.
Implementatie in Python en R
Laten we ons eerdere voorbeeld valideren: het berekenen van de kans om precies 5 niet-defecte eenheden te krijgen voordat we de derde defecte vinden (r=3, p=0.1).
Python-implementatie
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # Bereken binomiaalcoëfficiënt (k+r-1 kiezen k) binom_coef = math.comb(k + r - 1, k) # Bereken p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # Onze voorbeeldparameters k = 5 # mislukkingen (niet-defecte eenheden) r = 3 # successen (defecte eenheden) p = 0.1 # kans op succes (defect) # Berekenen met behulp van onze functie prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # Verifiëren met scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
De bovenstaande codefragment zou het volgende moeten opleveren:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R-implementatie
# Bereken kansmassafunctie k <- 5 # mislukkingen (niet-defecte eenheden) r <- 3 # successen (defecte eenheden) p <- 0.1 # kans op succes (defect) # Gebruikmakend van dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # Handmatige berekening ter verificatie manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
Het bovenstaande codefragment zou dezelfde getallen moeten uitvoeren als in ons Python-voorbeeld:
R calculation: 0.0124 Manual Calculation: 0.0124
Beide implementaties bevestigen onze eerder berekende waarschijnlijkheid van ongeveer 0,0124 of 1,24%.
Relatie tot Andere Verdelingen
Het begrijpen van hoe de negatieve binomiale verdeling verband houdt met andere waarschijnlijkheidsverdelingen helpt verduidelijken wanneer elke verdeling moet worden gebruikt. De negatieve binomiale verdeling heeft unieke verbindingen met verschillende belangrijke verdelingen in de statistiek.
Negatieve binomiale verdeling vs. binomiale verdeling
De binomiale verdeling dient als een fundamenteel vertrekpunt. Terwijl de binomiale verdeling successen telt in een vast aantal proeven, draait de negatieve binomiale dit concept om door de proeven te tellen die nodig zijn voor een vast aantal successen. Deze verdelingen zijn complementair – als je precies 3 successen nodig hebt en wilt weten wat de kans is om dit te bereiken in precies 8 proeven, gebruik dan de binomiale verdeling. Als je wilt weten wat de kans is dat je precies 8 proeven nodig hebt om 3 successen te behalen, gebruik dan de negatieve binomiale.
Negatieve binomiale verdeling vs. Poissonverdeling
De Poissonverdeling wordt vaak vergeleken met de negatieve binomiale bij het modelleren van telgegevens. Beide behandelen discrete gebeurtenissen, maar ze verschillen in hun variantie-verwachtingen. Het kenmerkende aspect van de Poissonverdeling is dat het gemiddelde gelijk is aan de variantie. Echter, telgegevens uit de echte wereld vertonen vaak overdispersie, waarbij de variantie het gemiddelde overschrijdt. De negatieve binomiale verdeling past zich van nature aan deze extra variabiliteit aan, waardoor deze geschikter is voor fenomenen zoals:
- Patronen van ziekte-uitbraken waarbij sommige gevallen leiden tot veel meer infecties
- Klachtengegevens van klanten waarbij sommige problemen meerdere gerelateerde klachten uitlokken
- Piek in websiteverkeer waarbij bepaalde gebeurtenissen verhoogde activiteitsniveaus veroorzaken
Negatieve binomiale verdeling versus geometrische verdeling
De geometrische verdeling komt naar voren als een speciaal geval van de negatieve binomiale verdeling wanneer we r=1 instellen, wat betekent dat we wachten op slechts één succes. Dit maakt het perfect voor het modelleren van scenario’s zoals:
- Aantal pogingen tot de eerste succes
- Tijd tot de eerste storing in betrouwbaarheidstests
- Aantal pogingen tot de eerste doorbraak in onderzoek
Negatieve binomiale verdeling als een Gamma-Poisson-mix
Tenslotte kan de negatieve binomiale verdeling worden afgeleid als een Gamma-Poisson-mix, wat een theoretische basis biedt voor zijn vermogen om overdispersie aan te pakken. Deze relatie helpt verklaren waarom de negatieve binomiale verdeling goed werkt in hiërarchische modellen waar individuele voorkomsttarieven variëren volgens een gammaverdeling.
Voordelen en Beperkingen
De negatieve binomiale verdeling biedt duidelijke voordelen die het waardevol maken voor het modelleren van verschijnselen in de echte wereld, maar heeft ook belangrijke beperkingen waar datawetenschappers rekening mee moeten houden.
| Advantages | Limitations |
|---|---|
| Flexibel om te gaan met oververspreide gegevens wanneer de variantie de gemiddelde waarde overschrijdt | Vereist onafhankelijkheid tussen tests/gebeurtenissen |
| Parameters hebben duidelijke interpretaties voor praktisch gebruik | Parameter schatting wordt onbetrouwbaar met kleine steekproeven |
| Accepteert zowel tellingen als verhoudingen | Rekenkundig intensiever dan eenvoudigere verdelingen |
| Modellen clustering in telgegevens op een natuurlijke manier | Kan overpassen wanneer de gegevens niet echt oververspreid zijn |
| Werkt goed met tijdreeksen en longitudinale gegevens | Gaat uit van een constante kans op succes over tests |
Negatieve binomiale regressie
Negatieve binomiale regressie breidt de traditionele regressie uit naar telgegevens, met name wanneer de gegevens overdispersie vertonen. Terwijl Poisson-regressie ervan uitgaat dat het gemiddelde gelijk is aan de variantie, ontspant negatieve binomiale regressie deze beperking, waardoor het meer geschikt is voor toepassingen in de echte wereld.
Stel je een callcenter scenario voor: We willen het aantal klantenservicegesprekken per uur voorspellen. Onze voorspellers kunnen zijn:
- Tijdstip van de dag
- Dag van de week
- Vakantiestatus
- Activiteit van marketingcampagnes
- Weersomstandigheden
Standaard Poissonregressie kan de variatie in belvolumes onderschatten, vooral tijdens piekuren of speciale evenementen. Negatieve binomiale regressie houdt rekening met deze extra variabiliteit, wat realistischere voorspellingen en betrouwbaarheidsintervallen oplevert.
Conclusie
Door zijn vermogen om complexe telgegevens te modelleren en overdispersie te hanteren, blijft de negatieve binomiale verdeling een essentieel hulpmiddel voor het begrijpen en voorspellen van fenomenen in de echte wereld. Zoals u hebt gezien, blinkt het uit in het modelleren van overgedisperse gegevens, biedt het flexibiliteit om een groot aantal verschillende scenario’s te modelleren, en het strekt zich zelfs natuurlijk uit tot regressieanalyse.
Als je geïnteresseerd bent in het verdiepen van je begrip van kansverdelingen en hun toepassingen, bieden onze Cursussen over Waarschijnlijkheid en Statistiek uitgebreide dekking van deze onderwerpen. Onze cursussen bevatten praktische oefeningen met datasets uit de echte wereld, waarmee je zowel theoretische concepten als praktische implementaties in Python en R onder de knie krijgt. Overweeg ook onze Carrièreroute Machine Learning Scientist in Python. Ik beloof je, je zult veel leren.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













