Nel mio decennale viaggio attraverso la finanza quantitativa, ho incontrato numerose distribuzioni statistiche, ma poche si sono dimostrate tanto intrigantemente denominate e praticamente utili quanto la distribuzione binomiale negativa. Analizzando schemi di trading e modelli di rischio, ho scoperto che questa distribuzione, nonostante il suo nome apparentemente pessimistico, offre insight nei processi di conteggio che molti modelli più semplici non riescono a catturare.
La distribuzione binomiale negativa fornisce un sofisticato quadro per modellare tali scenari, offrendo una maggiore flessibilità rispetto ai suoi controparti più semplici come la distribuzione di Poisson. Essa funge da estensione naturale della distribuzione binomiale, adattandosi a situazioni in cui è necessario modellare il numero di prove fino a quando si verifichi un certo numero di eventi, piuttosto che il numero di eventi in un numero fisso di prove.
In questa guida completa, esploreremo le fondamenta matematiche della distribuzione binomiale negativa, le sue applicazioni pratiche e l’implementazione in Python e R. Partendo dalle sue proprietà di base e passando alle applicazioni avanzate, costruiremo una comprensione approfondita di questo potente strumento statistico.
Cosa è la Distribuzione Binomiale Negativa?
La distribuzione binomiale negativa ha avuto origine nel 18° secolo attraverso lo studio della probabilità nei giochi d’azzardo. Questa distribuzione di probabilità discreta modella il numero di fallimenti in una sequenza di prove di Bernoulli indipendenti prima di raggiungere un numero predeterminato di successi. Ogni prova deve essere indipendente e avere la stessa probabilità di successo.
Per comprendere intuitivamente questa distribuzione, considera un semplice esperimento: intervistare candidati fino a trovare tre persone qualificate per una posizione. La distribuzione modellerebbe il numero di interviste non riuscite (fallimenti) necessarie prima di trovare queste tre persone qualificate (successi). Questo differisce fondamentalmente dalla distribuzione binomiale, che invece modella il numero di successi in un numero fisso di prove – come il numero di candidati qualificati trovati esattamente in 20 interviste.
Quindi puoi vedere, anche se il nome “binomiale negativo” potrebbe far alzare le sopracciglia, non implica nulla di negativo nel senso convenzionale. L’aspetto “negativo” deriva dalla sua derivazione storica che coinvolge esponenti negativi.
Dove viene utilizzata la distribuzione binomiale negativa
La distribuzione binomiale negativa è utilizzata in molti modi diversi. Viene utilizzata in finanza, che è dove la colloco maggiormente, dove modella scenari come il numero di giorni di negoziazione necessari per raggiungere un livello di profitto target, o il numero di domande di credito esaminate prima di trovare un certo numero di mutuatari qualificati.
In generale, la distribuzione binomiale negativa si è dimostrata utile anche per modellare dati di conteggio quando la varianza supera la media, un fenomeno noto come sovradispersione. Mentre la distribuzione di Poisson assume che la media sia uguale alla varianza, i dati di conteggio del mondo reale mostrano spesso una maggiore variabilità. Ad esempio, in epidemiologia, il numero di casi di malattia spesso varia più di quanto prevederebbe un modello di Poisson, rendendo la distribuzione binomiale negativa più adatta per modellare la diffusione della malattia.
Genetisti fanno affidamento su questa distribuzione nell’analisi dei dati di sequenziamento. Negli esperimenti di sequenziamento dell’RNA, i geni mostrano livelli di espressione variabili con alta variabilità. La distribuzione binomiale negativa modella il numero di letture di sequenza mappate su ciascun gene, tenendo conto sia della variabilità tecnica che biologica. Questo aiuta a identificare i geni differenzialmente espressi in modo più accurato rispetto ai metodi che assumono una varianza costante.
Negli studi ecologici, i ricercatori lo utilizzano per modellare l’abbondanza delle specie. Consideriamo lo studio delle popolazioni di uccelli: alcune aree potrebbero avere pochi uccelli mentre altre hanno grandi gruppi, creando una varianza maggiore del previsto. La binomiale negativa modella efficacemente queste distribuzioni raggruppate, aiutando gli ecologisti a comprendere la dinamica delle popolazioni e pianificare gli sforzi di conservazione.
Caratteristiche della distribuzione binomiale negativa
La distribuzione binomiale negativa è caratterizzata da due parametri chiave che ne determinano la forma e il comportamento. Comprendere questi parametri e la rappresentazione matematica ci aiuta a capire come questa distribuzione modella i fenomeni del mondo reale. Esploriamo sistematicamente queste caratteristiche.
Rappresentazione matematica e parametri
La distribuzione binomiale negativa ha due parametri fondamentali:
- r – il numero target di successi (un numero intero positivo)
-
Questi parametri modellano il comportamento della distribuzione. Consideriamo il tracciamento del numero di chiamate di vendita necessarie per ottenere cinque nuovi clienti (r = 5) quando ogni chiamata ha una probabilità di successo del 20% (p = 0.2). Il valore di r determina il nostro punto di arresto, mentre p influenza per quanto tempo potremmo continuare a effettuare chiamate.
Quando aumentiamo r mantenendo costante p, la distribuzione si sposta verso destra e diventa più dispersa, riflettendo il fatto che sono necessari più tentativi per ottenere più successi. Al contrario, quando aumentiamo p mantenendo costante r, la distribuzione si sposta verso sinistra e diventa più concentrata, indicando che di solito sono necessari meno tentativi quando il successo è più probabile.
Funzione di massa di probabilità (PMF) e funzione di distribuzione cumulativa (CDF)
La funzione di massa di probabilità ci fornisce la probabilità di richiedere esattamente k fallimenti prima di ottenere r successi. Per la distribuzione binomiale negativa, la PMF è:
Dove:
- X rappresenta il numero di fallimenti prima di ottenere r successi
- (k+r-1 scegli k) è il coefficiente binomiale, che rappresenta il numero di modi per disporre k fallimenti e r-1 successi
- p è la probabilità di successo
- r è il numero desiderato di successi
- K è il numero di fallimenti
Esempio: Nel controllo della qualità, se abbiamo bisogno di 3 unità difettose (r = 3) e ogni unità ha una probabilità del 10% di essere difettosa (p = 0,1), possiamo calcolare probabilità specifiche. Ad esempio, la probabilità di ottenere esattamente 5 unità non difettose (k = 5) prima di trovare la terza difettosa è:
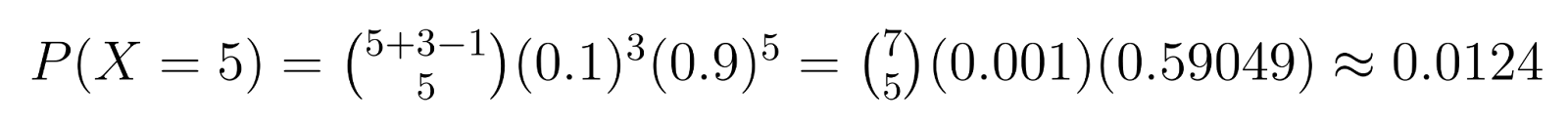
Questo calcolo mostra circa una probabilità del 1,24% di aver bisogno esattamente di 5 unità non difettose prima di trovare la terza difettosa.
La funzione di distribuzione cumulativa (CDF) si basa sulla PMF, dandoci la probabilità di richiedere k o meno fallimenti prima di raggiungere il nostro numero target di successi:
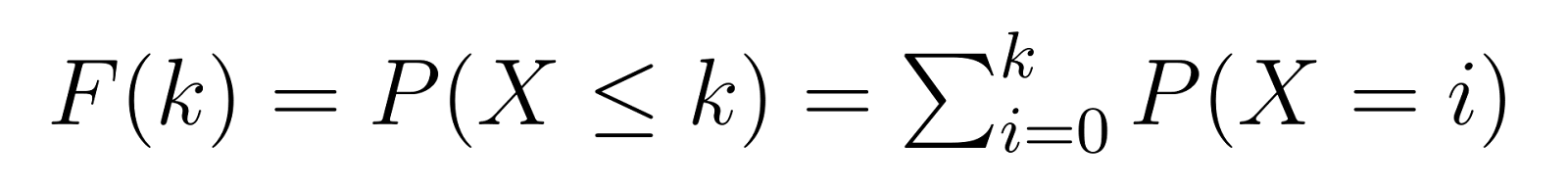
Questo significa che F(k) ci dà la probabilità di aver bisogno di al massimo k unità non difettose prima di trovare la terza difettosa. Ad esempio, F(5) ci darebbe la probabilità di aver bisogno di 5 o meno unità non difettose.
Media e varianza
La media (valore atteso) e la varianza della distribuzione binomiale negativa hanno formule eleganti che rivelano importanti proprietà sulla media (μ) e la varianza (σ²).
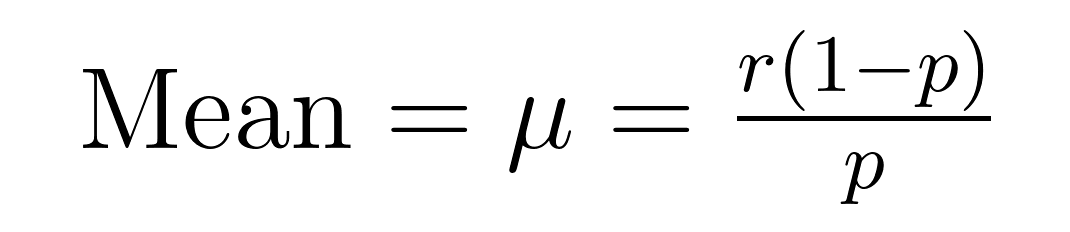
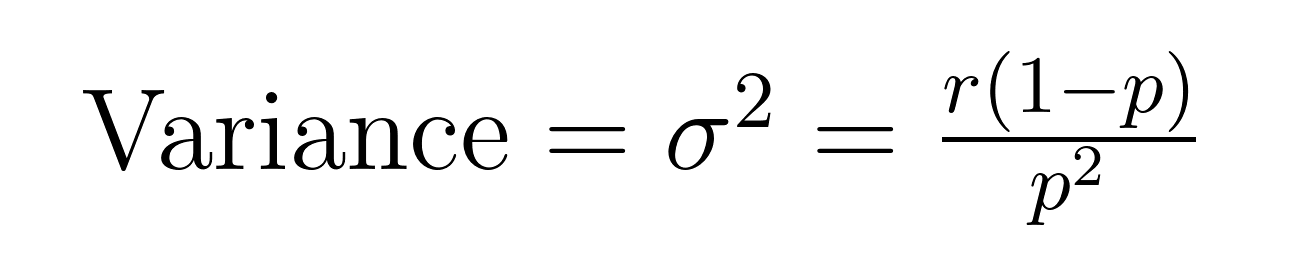
Queste formule dimostrano perché questa distribuzione eccelle nel modellare dati sovradispersi. Si noti che la varianza è sempre maggiore della media di un fattore pari a 1/p. Questa proprietà integrata la rende naturalmente adatta per dataset in cui la variabilità supera la media.
Ad esempio, se stiamo modellando chiamate di assistenza clienti in cui ci aspettiamo di risolvere 5 casi (r = 5) con un tasso di successo del 20% per tentativo (p = 0,2), il numero atteso di tentativi falliti sarebbe:
- Media = 5(1-0,2)/0,2 = 20 fallimenti
- Varianza = 5(1-0,2)/0,2² = 100
Questa maggiore varianza tiene conto del fatto che alcuni casi potrebbero essere risolti rapidamente mentre altri richiedono molti più tentativi, un pattern spesso osservato in scenari reali.
Comprendere queste caratteristiche ci aiuta a riconoscere quando applicare la distribuzione binomiale negativa e come interpretare efficacemente i suoi risultati. Queste fondamenta matematiche preparano il terreno per applicazioni pratiche e implementazioni, che esploreremo nelle sezioni successive.
Implementazione in Python e R
Validiamo il nostro esempio precedente: calcolando la probabilità di ottenere esattamente 5 unità non difettose prima di trovare la terza difettosa (r=3, p=0.1).
Implementazione in Python
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # Calcolare il coefficiente binomiale (k+r-1 scegli k) binom_coef = math.comb(k + r - 1, k) # Calcolare p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # I nostri parametri di esempio k = 5 # fallimenti (unità non difettose) r = 3 # successi (unità difettose) p = 0.1 # probabilità di successo (difettose) # Calcolare usando la nostra funzione prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # Verificare usando scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
Il frammento di codice sopra dovrebbe produrre quanto segue:
Manual calculation: 0.0124 SciPy calculation: 0.0124
Implementazione in R
# Calcolare la funzione di massa di probabilità k <- 5 # fallimenti (unità non difettose) r <- 3 # successi (unità difettose) p <- 0.1 # probabilità di successo (difettose) # Usando dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # Calcolo manuale per verifica manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
Il frammento di codice sopra dovrebbe produrre gli stessi numeri dell’esempio in Python:
R calculation: 0.0124 Manual Calculation: 0.0124
Entrambe le implementazioni confermano la nostra precedente probabilità calcolata di circa 0,0124 o 1,24%.
Relazione con Altre Distribuzioni
Comprendere come la distribuzione binomiale negativa si relaziona con altre distribuzioni di probabilità aiuta a chiarire quando utilizzarne una. La distribuzione binomiale negativa ha connessioni uniche con diverse distribuzioni importanti in statistica.
Distribuzione binomiale negativa vs. distribuzione binomiale
La distribuzione binomiale serve come punto di partenza fondamentale. Mentre la distribuzione binomiale conta i successi in un numero fisso di prove, la binomiale negativa ribalta questo concetto contando le prove necessarie per un numero fisso di successi. Queste distribuzioni sono complementari: se hai bisogno esattamente di 3 successi e vuoi conoscere la probabilità di ottenere questo risultato esattamente in 8 prove, usa la distribuzione binomiale. Se vuoi conoscere la probabilità di aver bisogno esattamente di 8 prove per ottenere 3 successi, usa la binomiale negativa.
Distribuzione binomiale negativa vs distribuzione di Poisson
La distribuzione di Poisson è spesso paragonata alla binomiale negativa nella modellazione dei dati di conteggio. Entrambe gestiscono eventi discreti, ma differiscono nelle loro ipotesi di varianza. La caratteristica distintiva della distribuzione di Poisson è che la sua media è uguale alla sua varianza. Tuttavia, i dati reali di conteggio spesso mostrano sovradispersione, in cui la varianza supera la media. La distribuzione binomiale negativa accoglie naturalmente questa variabilità aggiuntiva, rendendola più adatta per fenomeni come:
- Modelli di epidemie in cui alcuni casi portano a molte più infezioni
- Dati delle lamentele dei clienti in cui alcuni problemi generano più lamentele correlate
- Picchi di traffico del sito web in cui determinati eventi causano livelli di attività elevati
Distribuzione binomiale negativa vs distribuzione geometrica
La distribuzione geometrica emerge come un caso speciale della binomiale negativa quando impostiamo r=1, il che significa che stiamo aspettando solo un successo. Questo la rende perfetta per modellare scenari come:
- Numero di tentativi fino al primo successo
- Tempo fino al primo fallimento nei test di affidabilità
- Numero di prove fino alla prima svolta nella ricerca
Distribuzione binomiale negativa come miscela Gamma-Poisson
Infine, la binomiale negativa può essere derivata come una miscela Gamma-Poisson, fornendo una base teorica per la sua capacità di gestire l’overdispersione. Questa relazione aiuta a spiegare perché la distribuzione binomiale negativa funziona bene nei modelli gerarchici in cui i tassi individuali di occorrenza variano secondo una distribuzione gamma.
Vantaggi e Limitazioni
La distribuzione binomiale negativa offre vantaggi distintivi che la rendono preziosa per la modellazione di fenomeni del mondo reale, pur avendo anche importanti limitazioni che gli scienziati dei dati dovrebbero considerare.
| Advantages | Limitations |
|---|---|
| Gestisce in modo flessibile i dati overdispersi quando la varianza supera la media | Richiede indipendenza tra prove/eventi |
| I parametri hanno interpretazioni chiare per un uso pratico | La stima dei parametri diventa inaffidabile con campioni piccoli |
| Accoglie sia conteggi che proporzioni | Computazionalmente più intensiva rispetto a distribuzioni più semplici |
| Modella naturalmente il raggruppamento nei dati di conteggio | Puo’ sovradattarsi quando i dati non sono realmente overdispersi |
| Funziona bene con dati di serie temporali e longitudinali | Assume una probabilità costante di successo tra le prove |
regressione binomiale negativa
La regressione binomiale negativa estende la regressione tradizionale ai dati di conteggio, in particolare quando i dati mostrano sovradispersione. Mentre la regressione di Poisson presume che la media sia uguale alla varianza, la regressione binomiale negativa allenta questo vincolo, rendendola più adatta per applicazioni nel mondo reale.
Considera uno scenario di call center: vogliamo prevedere il numero di chiamate al servizio clienti per ora. I nostri predittori potrebbero includere:
- Ora del giorno
- Giorno della settimana
- Stato festivo
- Attività della campagna di marketing
- Condizioni meteorologiche
La regressione di Poisson standard potrebbe sottovalutare la variazione nei volumi delle chiamate, specialmente durante le ore di punta o eventi speciali. La regressione binomiale negativa tiene conto di questa variabilità aggiuntiva, fornendo previsioni più realistiche e intervalli di confidenza.
Conclusion
Attraverso la sua capacità di modellare dati di conteggio complessi e gestire sovradispersione, la distribuzione binomiale negativa rimane uno strumento essenziale per comprendere e prevedere fenomeni del mondo reale. Come hai visto, eccelle nel modellare dati sovradispersi, fornisce flessibilità per modellare un gran numero di scenari diversi e si estende naturalmente anche all’analisi di regressione.
Se sei interessato a approfondire la tua comprensione delle distribuzioni di probabilità e delle loro applicazioni, i nostri corsi di Probabilità e Statistica offrono una copertura completa di questi argomenti. I nostri corsi includono esercitazioni pratiche con set di dati del mondo reale, aiutandoti a padroneggiare sia concetti teorici che implementazioni pratiche in Python e R. Inoltre, considera il nostro percorso professionale Scienziato dell’Apprendimento Automatico in Python. Prometto che imparerai molto.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













