In meiner jahrzehntelangen Reise durch die quantitative Finanzwirtschaft bin ich auf zahlreiche statistische Verteilungen gestoßen, aber wenige haben sich als so interessant benannt und gleichzeitig praktisch wertvoll erwiesen wie die negative binomiale Verteilung. Bei der Analyse von Handelsmustern und Risikomodellen entdeckte ich, dass diese Verteilung, trotz ihres scheinbar pessimistischen Namens, Einblicke in Zählprozesse bietet, die viele einfachere Modelle nicht erfassen können.
Die negative binomiale Verteilung bietet einen raffinierten Rahmen zur Modellierung solcher Szenarien und bietet mehr Flexibilität als ihre einfacheren Gegenstücke wie die Poisson-Verteilung. Sie dient als natürliche Erweiterung der binomialen Verteilung und passt sich Situationen an, in denen wir die Anzahl der Versuche modellieren müssen, bis eine bestimmte Anzahl von Ereignissen eintritt, anstatt die Anzahl der Ereignisse in einer festen Anzahl von Versuchen.
In diesem umfassenden Leitfaden werden wir die mathematischen Grundlagen der negativen binomialen Verteilung, praktische Anwendungen und die Implementierung in Python und R untersuchen. Beginnend mit ihren grundlegenden Eigenschaften und weiter zu fortgeschrittenen Anwendungen werden wir ein gründliches Verständnis dieses leistungsstarken statistischen Werkzeugs aufbauen.
Was ist die negative binomiale Verteilung?
Die negative binomiale Verteilung entstand im 18. Jahrhundert durch die Untersuchung der Wahrscheinlichkeit bei Glücksspielen. Diese diskrete Wahrscheinlichkeitsverteilung modelliert die Anzahl an Misserfolgen in einer Abfolge von unabhängigen Bernoulli-Versuchen, bevor eine vorher festgelegte Anzahl an Erfolgen erreicht wird. Jeder Versuch muss unabhängig sein und die gleiche Wahrscheinlichkeit für Erfolg haben.
Um diese Verteilung intuitiv zu verstehen, stelle dir ein einfaches Experiment vor: Bewerbungsgespräche führen, bis drei qualifizierte Kandidaten für eine Position gefunden sind. Die Verteilung würde die Anzahl an erfolglosen Bewerbungsgesprächen (Misserfolge) modellieren, die benötigt werden, bevor diese drei qualifizierten Kandidaten (Erfolge) gefunden sind. Dies unterscheidet sich grundlegend von der binomialen Verteilung, die stattdessen die Anzahl an Erfolgen in einer festen Anzahl von Versuchen modelliert – wie die Anzahl an qualifizierten Kandidaten, die in genau 20 Bewerbungsgesprächen gefunden werden.
Wie Sie sehen können, bedeutet der Name „negative Binomialverteilung“ trotz möglicher hochgezogener Augenbrauen nichts Negatives im herkömmlichen Sinne. Der „negative“ Aspekt stammt von ihrer historischen Ableitung, die negative Exponenten beinhaltet.
Wo die Negative Binomialverteilung Verwendet Wird
Die negative Binomialverteilung wird auf viele verschiedene Arten verwendet. Sie findet Anwendung in der Finanzwirtschaft, wo ich sie am häufigsten einordne, da sie Szenarien modelliert, wie die Anzahl der Handelstage bis zum Erreichen eines Zielgewinnniveaus oder die Anzahl der geprüften Kreditanträge, bevor eine bestimmte Anzahl qualifizierter Kreditnehmer gefunden wird.
Allgemeiner gesagt, hat sich die negative binomiale Verteilung auch als wertvoll für die Modellierung von Zähl-Daten erwiesen, wenn die Varianz den Mittelwert übersteigt, ein Phänomen, das als Überdispersion bekannt ist. Während die Poisson-Verteilung annimmt, dass der Mittelwert gleich der Varianz ist, zeigt die Zähl-Daten aus der realen Welt oft eine größere Variabilität. Zum Beispiel variiert in der Epidemiologie die Anzahl der Krankheitsfälle oft mehr, als es ein Poisson-Modell vorhersagen würde, was die negative binomiale Verteilung geeigneter für die Modellierung der Krankheitsausbreitung macht.
Genetiker verlassen sich auf diese Verteilung, wenn sie Sequenzierungsdaten analysieren. In RNA-Sequenzierungsversuchen zeigen Gene unterschiedliche Expressionsniveaus mit hoher Variabilität. Die negative Binomialverteilung modelliert die Anzahl der Sequenzlesungen, die auf jedes Gen abgebildet sind, und berücksichtigt sowohl technische als auch biologische Variationen. Dies hilft, differentiell exprimierte Gene genauer zu identifizieren als Methoden, die von einer konstanten Varianz ausgehen.
In ökologischen Studien verwenden Forscher es, um Artenhäufigkeit zu modellieren. Betrachten wir die Untersuchung von Vogelpopulationen: Einige Gebiete haben möglicherweise nur wenige Vögel, während in anderen große Gruppen vorhanden sind, was zu einer höheren Varianz als erwartet führt. Die negative Binomialverteilung modelliert diese gruppierten Verteilungen effektiv und hilft Ökologen, Populationdynamiken zu verstehen und Naturschutzmaßnahmen zu planen.
Merkmale der negativen Binomialverteilung
Die negative Binomialverteilung wird durch zwei Schlüsselparameter charakterisiert, die ihre Form und ihr Verhalten bestimmen. Das Verständnis dieser Parameter und der mathematischen Darstellung hilft uns zu verstehen, wie diese Verteilung Phänomene in der realen Welt modelliert. Lassen Sie uns diese Merkmale systematisch erkunden.
Mathematische Darstellung und Parameter
Die negative Binomialverteilung hat zwei grundlegende Parameter:
- r – Die Zielanzahl an Erfolgen (eine positive ganze Zahl)
- p – Die Wahrscheinlichkeit des Erfolgs bei jedem Versuch (zwischen 0 und 1)
Diese Parameter bestimmen, wie sich die Verteilung verhält. Betrachten Sie das Verfolgen der Anzahl von Verkaufsgesprächen, die benötigt werden, um fünf neue Kunden zu gewinnen (r = 5), wenn jeder Anruf eine Erfolgswahrscheinlichkeit von 20% hat (p = 0,2). Der Wert von r bestimmt unseren Stopppunkt, während p beeinflusst, wie lange wir voraussichtlich Anrufe tätigen werden.
Wenn wir r erhöhen, während wir p konstant halten, verschiebt sich die Verteilung nach rechts und wird breiter, was darauf hindeutet, dass wir mehr Versuche benötigen, um mehr Erfolge zu erzielen. Umgekehrt, wenn wir p erhöhen, während wir r konstant halten, verschiebt sich die Verteilung nach links und wird konzentrierter, was darauf hinweist, dass in der Regel weniger Versuche erforderlich sind, wenn der Erfolg wahrscheinlicher ist.
Wahrscheinlichkeitsmassenfunktion (PMF) und kumulative Verteilungsfunktion (CDF)
Die Wahrscheinlichkeitsmassefunktion gibt uns die Wahrscheinlichkeit, genau k Misserfolge zu benötigen, bevor r Erfolge erzielt werden. Für die negative Binomialverteilung lautet die PMF:
Wo:
- X repräsentiert die Anzahl der Misserfolge vor dem Erreichen von r Erfolgen
- (k+r-1 über k) ist der Binomialkoeffizient, der die Anzahl der Möglichkeiten darstellt, k Misserfolge und r-1 Erfolge anzuordnen
- p ist die Erfolgswahrscheinlichkeit
- r ist die gewünschte Anzahl von Erfolgen
- K ist die Anzahl der Misserfolge
Beispiel: In der Qualitätskontrolle, wenn wir 3 fehlerhafte Einheiten benötigen (r = 3) und jede Einheit eine 10% ige Chance hat, fehlerhaft zu sein (p = 0,1), können wir spezifische Wahrscheinlichkeiten berechnen. Zum Beispiel ist die Wahrscheinlichkeit, genau 5 nicht fehlerhafte Einheiten zu erhalten (k = 5), bevor wir die dritte fehlerhafte finden:
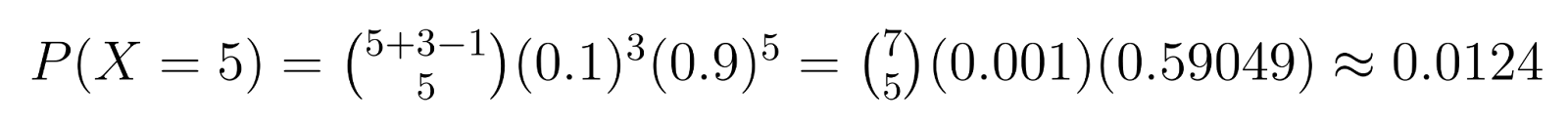
Diese Berechnung zeigt eine Chance von etwa 1,24%, genau 5 nicht fehlerhafte Einheiten zu benötigen, bevor die dritte fehlerhafte gefunden wird.
Die kumulative Verteilungsfunktion (CDF) baut auf der PMF auf und gibt uns die Wahrscheinlichkeit, k oder weniger Misserfolge zu benötigen, bevor wir unsere Zielanzahl von Erfolgen erreichen:
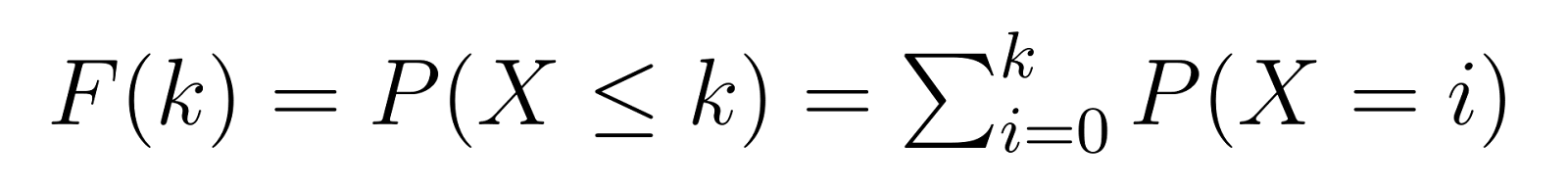
Dies bedeutet, dass F(k) uns die Wahrscheinlichkeit gibt, höchstens k nicht fehlerhafte Einheiten zu benötigen, bevor wir unsere dritte fehlerhafte finden. Zum Beispiel würde uns F(5) die Wahrscheinlichkeit geben, 5 oder weniger nicht fehlerhafte Einheiten zu benötigen.
Mittelwert und Varianz
Der Erwartungswert und die Varianz der negativen Binomialverteilung haben elegante Formeln, die wichtige Eigenschaften über den Erwartungswert (μ) und die Varianz (σ²) offenbaren.
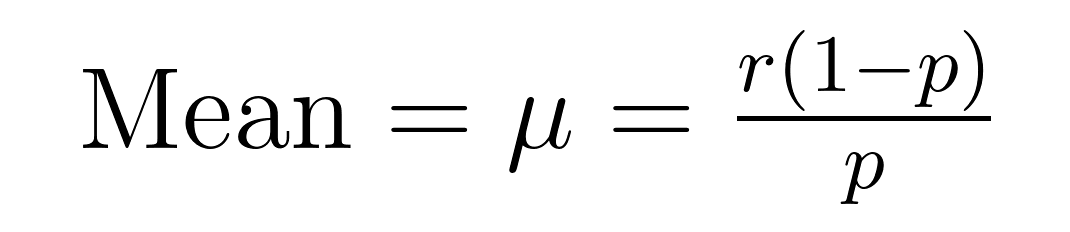
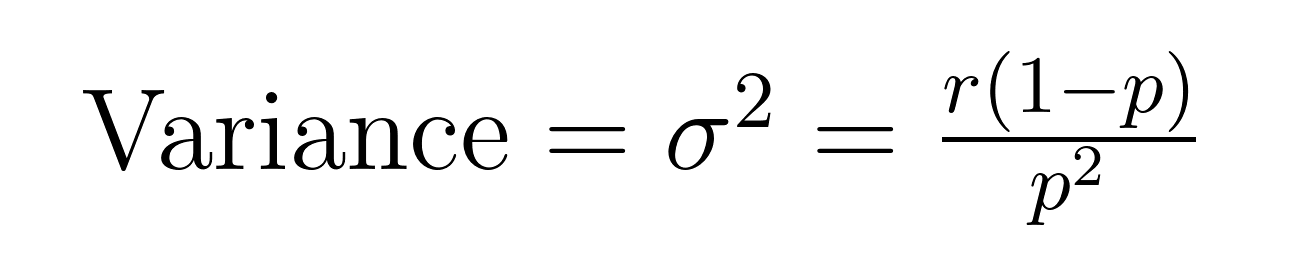
Diese Formeln zeigen, warum diese Verteilung sich zur Modellierung von überdispersen Daten eignet. Beachten Sie, dass die Varianz immer um einen Faktor von 1/p größer ist als der Mittelwert. Diese eingebaute Eigenschaft macht sie natürlicherweise für Datensätze geeignet, bei denen die Variabilität den Durchschnitt übersteigt.
Zum Beispiel, wenn wir Anrufe im Kundenservice modellieren, bei denen wir erwarten, 5 Fälle (r = 5) mit einer Erfolgsquote von 20% pro Versuch (p = 0,2) lösen zu können, wäre die erwartete Anzahl der fehlgeschlagenen Versuche:
- Mittelwert = 5(1-0,2)/0,2 = 20 Misserfolge
- Varianz = 5(1-0,2)/0,2² = 100
Diese höhere Varianz berücksichtigt die Realität, dass einige Fälle schnell gelöst werden können, während andere viele weitere Versuche erfordern, ein Muster, das oft in realen Szenarien beobachtet wird.
Das Verständnis dieser Merkmale hilft uns zu erkennen, wann wir die negative binomiale Verteilung anwenden sollten und wie wir ihre Ergebnisse effektiv interpretieren können. Diese mathematischen Grundlagen schaffen die Basis für praktische Anwendungen und Implementierungen, die wir in den folgenden Abschnitten erkunden werden.
Implementierung in Python und R
Lasst uns unser früheres Beispiel validieren: die Wahrscheinlichkeit zu berechnen, genau 5 nicht defekte Einheiten zu erhalten, bevor wir die dritte defekte finden (r=3, p=0.1).
Python-Implementierung
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # Berechnen Sie den Binomialkoeffizienten (k+r-1 wählen k) binom_coef = math.comb(k + r - 1, k) # Berechnen Sie p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # Unsere Beispielparameter k = 5 # Misserfolge (nicht-defekte Einheiten) r = 3 # Erfolge (defekte Einheiten) p = 0.1 # Erfolgswahrscheinlichkeit (defekt) # Berechnen Sie mit unserer Funktion prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # Überprüfen Sie mit scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
Der obige Code-Schnipsel sollte folgendes ausgeben:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R-Implementierung
# Berechnen der Wahrscheinlichkeitsmassefunktion k <- 5 # Misserfolge (nicht-defekte Einheiten) r <- 3 # Erfolge (defekte Einheiten) p <- 0.1 # Erfolgswahrscheinlichkeit (defekt) # Mit dnbinom verwenden prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # Manuelle Berechnung zur Überprüfung manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
Der obige Code-Schnipsel sollte dieselben Zahlen ausgeben wie unser Python-Beispiel:
R calculation: 0.0124 Manual Calculation: 0.0124
Beide Implementierungen bestätigen unsere zuvor berechnete Wahrscheinlichkeit von ungefähr 0,0124 oder 1,24 %.
Zusammenhang mit anderen Verteilungen
Zu verstehen, wie die negative Binomialverteilung mit anderen Wahrscheinlichkeitsverteilungen zusammenhängt, hilft dabei, zu klären, wann jede einzelne verwendet werden sollte. Die negative Binomialverteilung hat einzigartige Verbindungen zu mehreren wichtigen Verteilungen in der Statistik.
Negative Binomialverteilung vs. Binomialverteilung
Die binomiale Verteilung dient als grundlegender Ausgangspunkt. Während die binomiale Verteilung Erfolge in einer festen Anzahl von Versuchen zählt, kehrt die negative binomiale Verteilung dieses Konzept um, indem sie die Versuche zählt, die für eine feste Anzahl von Erfolgen benötigt werden. Diese Verteilungen ergänzen sich – wenn Sie genau 3 Erfolge benötigen und die Wahrscheinlichkeit kennen möchten, dies in genau 8 Versuchen zu erreichen, verwenden Sie die binomiale Verteilung. Wenn Sie die Wahrscheinlichkeit kennen möchten, genau 8 Versuche zu benötigen, um 3 Erfolge zu erzielen, verwenden Sie die negative binomiale Verteilung.
Negative binomiale Verteilung vs. Poisson-Verteilung
Die Poisson-Verteilung wird oft mit der negativen binomialen Verteilung verglichen, wenn Zähldaten modelliert werden. Beide behandeln diskrete Ereignisse, unterscheiden sich jedoch in ihren Varianzannahmen. Das charakteristische Merkmal der Poisson-Verteilung ist, dass ihr Mittelwert gleich ihrer Varianz ist. Allerdings zeigen Zähldaten aus der realen Welt häufig Überdispersion, bei der die Varianz den Mittelwert übersteigt. Die negative binomiale Verteilung berücksichtigt diese zusätzliche Variabilität auf natürliche Weise und eignet sich daher besser für Phänomene wie:
- Ausbruchsmuster von Krankheiten, bei denen einige Fälle zu vielen weiteren Infektionen führen
- Kundendienstbeschwerdedaten, bei denen einige Probleme mehrere verwandte Beschwerden auslösen
- Website-Traffic-Spitzen, bei denen bestimmte Ereignisse erhöhte Aktivitätsniveaus verursachen
Negative binomiale Verteilung vs. geometrische Verteilung
Die geometrische Verteilung tritt als ein Spezialfall der negativen binomialen Verteilung auf, wenn wir r=1 setzen, was bedeutet, dass wir nur auf einen Erfolg warten. Dies macht sie perfekt für die Modellierung von Szenarien wie:
- Anzahl der Versuche bis zum ersten Erfolg
- Zeit bis zum ersten Ausfall bei Zuverlässigkeitstests
- Anzahl der Versuche bis zum ersten Durchbruch in der Forschung
Negative binomiale Verteilung als Gamma-Poisson-Mischung
Schließlich kann die negative binomiale Verteilung als Gamma-Poisson-Mischung abgeleitet werden, was eine theoretische Grundlage für ihre Fähigkeit bietet, Überdispersion zu behandeln. Diese Beziehung hilft zu erklären, warum die negative binomiale Verteilung in hierarchischen Modellen gut funktioniert, in denen die individuellen Auftretensraten gemäß einer Gamma-Verteilung variieren.
Vorteile und Einschränkungen
Die negative binomiale Verteilung bietet deutliche Vorteile, die sie wertvoll für die Modellierung realer Phänomene machen, hat jedoch auch wichtige Einschränkungen, die Datenwissenschaftler berücksichtigen sollten.
| Advantages | Limitations |
|---|---|
| Handhabt Überdispersion flexibel, wenn die Varianz den Mittelwert übersteigt | Erfordert Unabhängigkeit zwischen Versuchen/Ereignissen |
| Parameter haben klare Interpretationen für die praktische Anwendung | Parameterabschätzungen werden bei kleinen Stichproben unzuverlässig |
| Berücksichtigt sowohl Zählungen als auch Anteile | Rechenintensiver als einfachere Verteilungen |
| Modelliert natürlich Clusterbildung in Zähldaten | Kann überanpassen, wenn die Daten nicht wirklich überdispersiert sind |
| Funktioniert gut mit Zeitreihen- und Längsschnittdaten | Geht von einer konstanten Erfolgswahrscheinlichkeit über alle Versuche aus |
Negative Binomial Regression
Die negative binomiale Regression erweitert die traditionelle Regression auf Zähldaten, insbesondere wenn die Daten eine Überdispersion zeigen. Während die Poisson-Regression annimmt, dass der Mittelwert der Varianz entspricht, lockert die negative binomiale Regression diese Einschränkung, wodurch sie besser für Anwendungen in der realen Welt geeignet ist.
Betrachten wir ein Szenario in einem Callcenter: Wir möchten die Anzahl der Kundenservice-Anrufe pro Stunde vorhersagen. Unsere Prädiktoren könnten Folgendes umfassen:
- Uhrzeit
- Wochentag
- Urlaubsstatus
- Aktivität von Marketingkampagnen
- Wetterbedingungen
Standard Poisson-Regression könnte die Variationen in den Anrufvolumina unterschätzen, insbesondere während der Spitzenzeiten oder bei besonderen Ereignissen. Die negative binomiale Regression berücksichtigt diese zusätzliche Variabilität und liefert realistischere Vorhersagen und Konfidenzintervalle.
Conclusion
Durch ihre Fähigkeit, komplexe Zähldaten zu modellieren und Überdispersion zu handhaben, bleibt die negative binomiale Verteilung ein unverzichtbares Werkzeug zum Verständnis und zur Vorhersage realer Phänomene. Wie Sie gesehen haben, zeichnet sie sich durch die Modellierung überdisperser Daten aus, bietet Flexibilität, um eine Vielzahl von Szenarien zu modellieren, und erstreckt sich sogar natürlich auf Regressionsanalysen.
Wenn Sie Ihr Verständnis für Wahrscheinlichkeitsverteilungen und deren Anwendungen vertiefen möchten, bieten unsere Kurse zu Wahrscheinlichkeit und Statistik eine umfassende Abdeckung dieser Themen. Unsere Kurse beinhalten praktische Übungen mit realen Datensätzen, die Ihnen helfen, sowohl theoretische Konzepte als auch praktische Implementierungen in Python und R zu beherrschen. Berücksichtigen Sie auch unseren Karriereweg zum Machine Learning Scientist in Python. Ich verspreche Ihnen, Sie werden viel lernen.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













