Na minha jornada de uma década pela finança quantitativa, encontrei inúmeras distribuições estatísticas, mas poucas se mostraram tão intrigantemente nomeadas e, ao mesmo tempo, valiosas na prática quanto a distribuição binomial negativa. Ao analisar padrões de negociação e modelos de risco, descobri que essa distribuição, apesar de seu nome aparentemente pessimista, oferece insights sobre processos de contagem que muitos modelos mais simples falham em capturar.
A distribuição binomial negativa fornece uma estrutura sofisticada para modelar tais cenários, oferecendo maior flexibilidade do que seus equivalentes mais simples, como a distribuição de Poisson. Ela serve como uma extensão natural da distribuição binomial, adaptando-se a situações em que precisamos modelar o número de tentativas até que um certo número de eventos ocorra, em vez do número de eventos em um número fixo de tentativas.
Neste guia abrangente, exploraremos as bases matemáticas da distribuição binomial negativa, suas aplicações práticas e sua implementação em Python e R. Começando por suas propriedades básicas e avançando para aplicações avançadas, construiremos uma compreensão profunda dessa poderosa ferramenta estatística.
O que é a Distribuição Binomial Negativa?
A distribuição binomial negativa originou-se no século XVIII através do estudo da probabilidade em jogos de azar. Esta distribuição de probabilidade discreta modela o número de falhas em uma sequência de experimentos de Bernoulli independentes antes de alcançar um número predeterminado de sucessos. Cada experimento deve ser independente e ter a mesma probabilidade de sucesso.
Para entender essa distribuição intuitivamente, considere um experimento simples: entrevistar candidatos até encontrar três qualificados para uma posição. A distribuição modelaria o número de entrevistas malsucedidas (falhas) necessárias antes de encontrar esses três candidatos qualificados (sucessos). Isso difere fundamentalmente da distribuição binomial, que modela em vez disso o número de sucessos em um número fixo de experimentos – como o número de candidatos qualificados encontrados em exatamente 20 entrevistas.
Como você pode ver, mesmo que o nome “binomial negativa” possa causar estranheza, não implica nada negativo no sentido convencional. O aspecto “negativo” deriva de sua origem histórica envolvendo expoentes negativos.
Onde a Distribuição Binomial Negativa é Usada
A distribuição binomial negativa é usada de muitas maneiras diferentes. É usada em finanças, que é onde eu mais a vejo, onde modela cenários como o número de dias de negociação até atingir um nível de lucro alvo, ou o número de solicitações de crédito analisadas antes de encontrar um certo número de mutuários qualificados.
De forma mais geral, a distribuição binomial negativa também se mostrou valiosa para modelar dados de contagem quando a variância excede a média, um fenômeno conhecido como sobredispersão. Enquanto a distribuição de Poisson assume que a média é igual à variância, os dados de contagem do mundo real frequentemente mostram maior variabilidade. Por exemplo, na epidemiologia, o número de casos de doenças geralmente varia mais do que um modelo de Poisson preveria, tornando a distribuição binomial negativa mais apropriada para modelar a propagação de doenças.
Geneticistas dependem dessa distribuição ao analisar dados de sequenciamento. Em experimentos de sequenciamento de RNA, os genes mostram níveis de expressão variados com alta variabilidade. A distribuição binomial negativa modela o número de leituras de sequência mapeadas para cada gene, levando em conta tanto a variação técnica quanto a biológica. Isso ajuda a identificar genes diferencialmente expressos de forma mais precisa do que métodos que assumem variância constante.
Nos estudos ecológicos, os pesquisadores a utilizam para modelar a abundância de espécies. Considere o estudo das populações de pássaros: algumas áreas podem ter poucos pássaros enquanto outras têm grandes aglomerados, criando uma variância maior do que o esperado. A binomial negativa modela efetivamente essas distribuições agrupadas, ajudando os ecologistas a compreender a dinâmica populacional e planejar esforços de conservação.
Características da Distribuição Binomial Negativa
A distribuição binomial negativa é caracterizada por dois parâmetros-chave que determinam sua forma e comportamento. Compreender esses parâmetros e a representação matemática nos ajuda a compreender como essa distribuição modela fenômenos do mundo real. Vamos explorar essas características sistematicamente.
Representação matemática e parâmetros
A distribuição binomial negativa possui dois parâmetros fundamentais:
- r – O número alvo de sucessos (um inteiro positivo)
- p – A probabilidade de sucesso em cada tentativa (entre 0 e 1)
Esses parâmetros moldam como a distribuição se comporta. Considere o acompanhamento do número de ligações de vendas necessárias para garantir cinco novos clientes (r = 5) quando cada ligação tem 20% de chance de sucesso (p = 0,2). O valor de r determina nosso ponto de parada, enquanto p influencia por quanto tempo podemos esperar continuar fazendo ligações.
Quando aumentamos r mantendo p constante, a distribuição se desloca para a direita e se torna mais dispersa, refletindo que precisamos de mais tentativas para alcançar mais sucessos. Por outro lado, quando aumentamos p mantendo r constante, a distribuição se desloca para a esquerda e se torna mais concentrada, indicando que geralmente são necessárias menos tentativas quando o sucesso é mais provável.
Função de massa de probabilidade (FMP) e função de distribuição cumulativa (FDC)
A função de massa de probabilidade nos dá a probabilidade de precisar exatamente de k falhas antes de alcançar r sucessos. Para a distribuição binomial negativa, a PMF é:
Onde:
- X representa o número de falhas antes de alcançar r sucessos
- (k+r-1 escolha k) é o coeficiente binomial, que representa o número de maneiras de arranjar k falhas e r-1 sucessos
- p é a probabilidade de sucesso
- r é o número desejado de sucessos
- K é o número de falhas
Exemplo: No controle de qualidade, se precisarmos de 3 unidades defeituosas (r = 3) e cada unidade tem uma chance de 10% de ser defeituosa (p = 0,1), podemos calcular probabilidades específicas. Por exemplo, a probabilidade de obter exatamente 5 unidades não defeituosas (k = 5) antes de encontrar a terceira unidade defeituosa é:
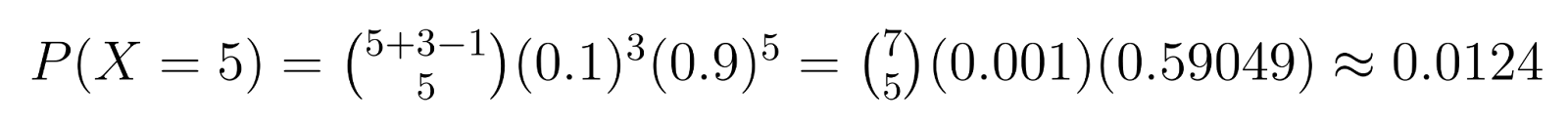
Esse cálculo mostra uma chance de cerca de 1,24% de precisar exatamente de 5 unidades não defeituosas antes de encontrar a terceira unidade defeituosa.
A função de distribuição acumulada (CDF) se baseia na PMF, nos dando a probabilidade de precisar de k ou menos falhas antes de alcançar nosso número alvo de sucessos:
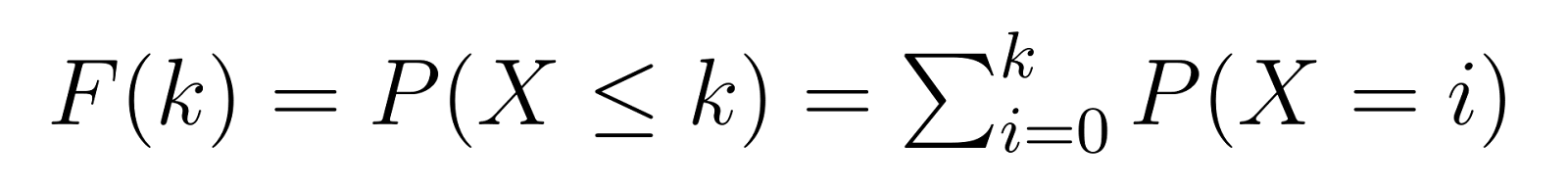
Isso significa que F(k) nos dá a probabilidade de precisar de no máximo k unidades não defeituosas antes de encontrar nossa terceira unidade defeituosa. Por exemplo, F(5) nos daria a probabilidade de precisar de 5 ou menos unidades não defeituosas.
Média e variância
A média (valor esperado) e variância da distribuição binomial negativa têm fórmulas elegantes que revelam propriedades importantes sobre a média (μ) e variância (σ²).
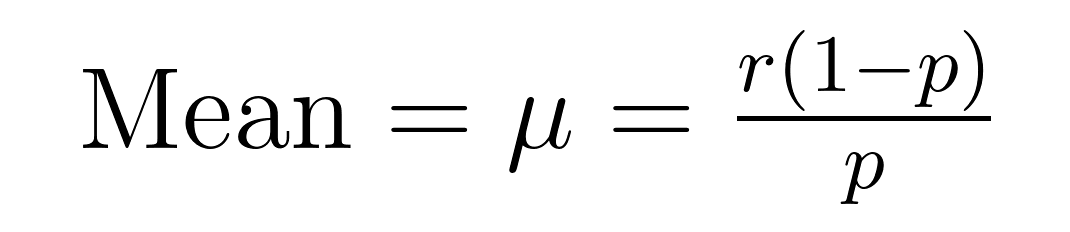
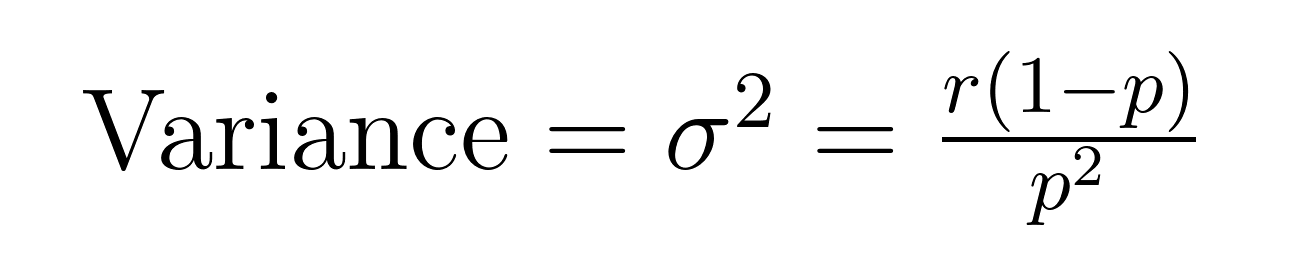
Essas fórmulas demonstram por que essa distribuição se destaca na modelagem de dados superdispersos. Note que a variância é sempre maior que a média por um fator de 1/p. Essa propriedade embutida a torna naturalmente adequada para conjuntos de dados onde a variabilidade excede a média.
Por exemplo, se estamos modelando chamadas de serviço ao cliente em que esperamos resolver 5 casos (r = 5) com uma taxa de sucesso de 20% por tentativa (p = 0,2), o número esperado de tentativas fracassadas seria:
- Média = 5(1-0,2)/0,2 = 20 falhas
- Variância = 5(1-0,2)/0,2² = 100
Essa maior variância leva em conta a realidade de que alguns casos podem ser resolvidos rapidamente, enquanto outros exigem muitas mais tentativas, um padrão frequentemente observado em cenários do mundo real.
Compreender essas características nos ajuda a reconhecer quando aplicar a distribuição binomial negativa e como interpretar seus resultados de forma eficaz. Essas fundações matemáticas preparam o terreno para aplicações práticas e implementação, que exploraremos nas seções subsequentes.
Implementação em Python e R
Vamos validar nosso exemplo anterior: calcular a probabilidade de obter exatamente 5 unidades não defeituosas antes de encontrar a terceira unidade defeituosa (r=3, p=0.1).
Implementação em Python
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # Calcular coeficiente binomial (k+r-1 escolha k) binom_coef = math.comb(k + r - 1, k) # Calcular p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # Nossos parâmetros de exemplo k = 5 # falhas (unidades não defeituosas) r = 3 # sucessos (unidades defeituosas) p = 0.1 # probabilidade de sucesso (defeituosa) # Calcular usando nossa função prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # Verificar usando scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
O trecho de código acima deve produzir a saída abaixo:
Manual calculation: 0.0124 SciPy calculation: 0.0124
Implementação em R
# Calcular função de massa de probabilidade k <- 5 # falhas (unidades não defeituosas) r <- 3 # sucessos (unidades defeituosas) p <- 0.1 # probabilidade de sucesso (defeituosa) # Usando dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # Cálculo manual para verificação manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
O trecho de código acima deve gerar os mesmos números que nosso exemplo em Python:
R calculation: 0.0124 Manual Calculation: 0.0124
Ambas as implementações confirmam nossa probabilidade calculada anteriormente de aproximadamente 0,0124 ou 1,24%.
Relação com Outras Distribuições
Entender como a distribuição binomial negativa se relaciona com outras distribuições de probabilidade ajuda a esclarecer quando usar cada uma. A distribuição binomial negativa tem conexões únicas com várias distribuições importantes em estatística.
Distribuição binomial negativa vs. distribuição binomial
A distribuição binomial serve como um ponto de partida fundamental. Enquanto a distribuição binomial conta sucessos em um número fixo de tentativas, a binomial negativa inverte esse conceito ao contar as tentativas necessárias para um número fixo de sucessos. Essas distribuições são complementares – se você precisa exatamente de 3 sucessos e quer saber a probabilidade de alcançá-los em exatamente 8 tentativas, use a distribuição binomial. Se você quer saber a probabilidade de precisar exatamente de 8 tentativas para obter 3 sucessos, use a binomial negativa.
Distribuição binomial negativa vs. distribuição de Poisson
A distribuição de Poisson é frequentemente comparada à binomial negativa ao modelar dados de contagem. Ambas lidam com eventos discretos, mas diferem em suas suposições de variância. A característica definidora da distribuição de Poisson é que sua média é igual à sua variância. No entanto, dados de contagem do mundo real frequentemente apresentam superdispersão, onde a variância excede a média. A distribuição binomial negativa acomoda naturalmente essa variabilidade extra, tornando-a mais adequada para fenômenos como:
- Padrões de surtos de doenças onde alguns casos levam a muitas mais infecções
- Dados de reclamações de clientes onde alguns problemas geram múltiplas reclamações relacionadas
- Picos de tráfego do site onde certos eventos causam níveis elevados de atividade
Distribuição binomial negativa vs. distribuição geométrica
A distribuição geométrica surge como um caso especial da distribuição binomial negativa quando definimos r=1, significando que estamos aguardando apenas um sucesso. Isso a torna perfeita para modelar cenários como:
- Número de tentativas até o primeiro sucesso
- Tempo até a primeira falha em testes de confiabilidade
- Número de tentativas até o primeiro avanço na pesquisa
Distribuição binomial negativa como uma mistura Gamma-Poisson
Finalmente, a binomial negativa pode ser derivada como uma mistura Gamma-Poisson, fornecendo uma base teórica para sua capacidade de lidar com sobredispersão. Essa relação ajuda a explicar por que a distribuição binomial negativa funciona bem em modelos hierárquicos onde as taxas individuais de ocorrência variam de acordo com uma distribuição gamma.
Vantagens e Limitações
A distribuição binomial negativa oferece vantagens distintas que a tornam valiosa para modelar fenômenos do mundo real, enquanto também possui limitações importantes que os cientistas de dados devem considerar.
| Advantages | Limitations |
|---|---|
| Gerencia flexivelmente dados sobredispersos quando a variância excede a média | Requer independência entre testes/eventos |
| Os parâmetros têm interpretações claras para uso prático | A estimativa de parâmetros torna-se pouco confiável com amostras pequenas |
| Accommodates both counts and proportions | Computacionalmente mais intensivo do que distribuições mais simples |
| Modelo naturalmente o agrupamento em dados de contagem | Pode sobreajustar quando os dados não estão verdadeiramente sobredispersos |
| Funciona bem com dados de séries temporais e longitudinais | Assume probabilidade constante de sucesso em todos os testes |
Regressão Binomial Negativa
A regressão binomial negativa estende a regressão tradicional para dados de contagem, especialmente quando os dados mostram superdispersão. Enquanto a regressão de Poisson assume que a média é igual à variância, a regressão binomial negativa relaxa essa restrição, tornando-a mais adequada para aplicações do mundo real.
Considere um cenário de centro de atendimento: queremos prever o número de chamadas de serviço ao cliente por hora. Nossos preditores podem incluir:
- Horário do dia
- Dia da semana
- Status de feriado
- Atividade de campanha de marketing
- Condições meteorológicas
A regressão de Poisson padrão pode subestimar a variação nos volumes de chamadas, especialmente durante horários de pico ou eventos especiais. A regressão binomial negativa leva em consideração essa variabilidade extra, fornecendo previsões e intervalos de confiança mais realistas.
Conclusão
Através de sua capacidade de modelar dados de contagem complexos e lidar com a superdispersão, a distribuição binomial negativa permanece uma ferramenta essencial para entender e prever fenômenos do mundo real. Como você viu, ela se destaca na modelagem de dados superdispersos, fornece flexibilidade para modelar uma grande variedade de cenários diferentes e até se estende naturalmente para análise de regressão.
Se você está interessado em aprofundar sua compreensão sobre distribuições de probabilidade e suas aplicações, nossos Cursos de Probabilidade e Estatística oferecem uma cobertura abrangente desses tópicos. Nossos cursos incluem exercícios práticos com conjuntos de dados do mundo real, ajudando você a dominar tanto os conceitos teóricos quanto as implementações práticas em Python e R. Além disso, considere nossa carreira de Cientista de Aprendizado de Máquina em Python. Eu prometo, você aprenderá muito.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













