In my decade-long journey through quantitative finance, I’ve encountered numerous statistical distributions, but few have proven as intriguingly named yet practically valuable as the negative binomial distribution. While analyzing trading patterns and risk models, I discovered that this distribution, despite its seemingly pessimistic name, offers insights into counting processes that many simpler models fail to capture.
The negative binomial distribution provides a sophisticated framework for modeling such scenarios, offering greater flexibility than its simpler counterparts like the Poisson distribution. It serves as a natural extension of the binomial distribution, adapting to situations where we need to model the number of trials until a certain number of events occur, rather than the number of events in a fixed number of trials.
In this comprehensive guide, we’ll explore the negative binomial distribution’s mathematical foundations, practical applications, and implementation in Python and R. Starting from its basic properties and moving to advanced applications, we’ll build a thorough understanding of this powerful statistical tool.
What is Negative Binomial Distribution?
The negative binomial distribution originated in the 18th century through the study of probability in games of chance. This discrete probability distribution models the number of failures in a sequence of independent Bernoulli trials before achieving a predetermined number of successes. Each trial must be independent and have the same probability of success.
To understand this distribution intuitively, consider a simple experiment: interviewing candidates until finding three qualified ones for a position. The distribution would model the number of unsuccessful interviews (failures) needed before finding these three qualified candidates (successes). This differs fundamentally from the binomial distribution, which instead models the number of successes in a fixed number of trials – such as the number of qualified candidates found in exactly 20 interviews.
So you can see, even though the name “negative binomial” might raise eyebrows, it doesn’t imply anything negative in the conventional sense. The “negative” aspect stems from its historical derivation involving negative exponents.
Where the Negative Binomial Distribution is Used
The negative binomial distribution is used in many different ways. It’s used in finance, which is where I most place it, where it models scenarios like the number of trading days until achieving a target profit level, or the number of credit applications reviewed before finding a certain number of qualified borrowers.
More generally, the negative binomial distribution has also proven valuable for modeling count data when the variance exceeds the mean, a phenomenon known as overdispersion. While the Poisson distribution assumes the mean equals the variance, real-world count data often shows greater variability. For instance, in epidemiology, the number of disease cases often varies more than a Poisson model would predict, making the negative binomial distribution more appropriate for modeling disease spread.
Geneticists rely on this distribution when analyzing sequencing data. In RNA sequencing experiments, genes show varying expression levels with high variability. The negative binomial models the number of sequence reads mapped to each gene, accounting for both technical and biological variation. This helps identify differentially expressed genes more accurately than methods assuming constant variance.
In ecological studies, researchers use it to model species abundance. Consider studying bird populations: some areas might have few birds while others have large clusters, creating higher variance than expected. The negative binomial effectively models these clustered distributions, helping ecologists understand population dynamics and plan conservation efforts.
Characteristics of the Negative Binomial Distribution
The negative binomial distribution is characterized by two key parameters that determine its shape and behavior. Understanding these parameters and the mathematical representation helps us grasp how this distribution models real-world phenomena. Let’s explore these characteristics systematically.
Mathematical representation and parameters
The negative binomial distribution has two fundamental parameters:
- r – The target number of successes (a positive integer)
- p – The probability of success on each trial (between 0 and 1)
These parameters shape how the distribution behaves. Consider tracking the number of sales calls needed to secure five new clients (r = 5) when each call has a 20% chance of success (p = 0.2). The value of r determines our stopping point, while p influences how long we might expect to keep making calls.
When we increase r while keeping p constant, the distribution shifts to the right and becomes more spread out, reflecting that we need more trials to achieve more successes. Conversely, when we increase p while keeping r constant, the distribution shifts to the left and becomes more concentrated, indicating fewer trials are typically needed when success is more likely.
Probability mass function (PMF) and cumulative distribution function (CDF)
The probability mass function gives us the probability of requiring exactly k failures before achieving r successes. For the negative binomial distribution, the PMF is:
Where:
- X represents the number of failures before achieving r successes
- (k+r-1 choose k) is the binomial coefficient, representing the number of ways to arrange k failures and r-1 successes
- p is the probability of success
- r is the desired number of successes
- K is the number of failures
Example: In quality control, if we need 3 defective units (r = 3) and each unit has a 10% chance of being defective (p = 0.1), we can calculate specific probabilities. For instance, the probability of getting exactly 5 non-defective units (k = 5) before finding the third defective one is:
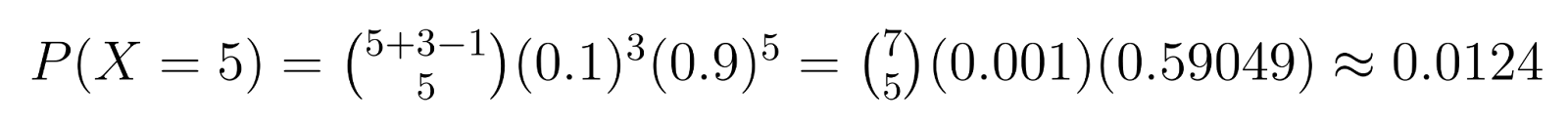
This calculation shows about a 1.24% chance of needing exactly 5 non-defective units before finding the third defective one.
The cumulative distribution function (CDF) builds upon the PMF, giving us the probability of requiring k or fewer failures before achieving our target number of successes:
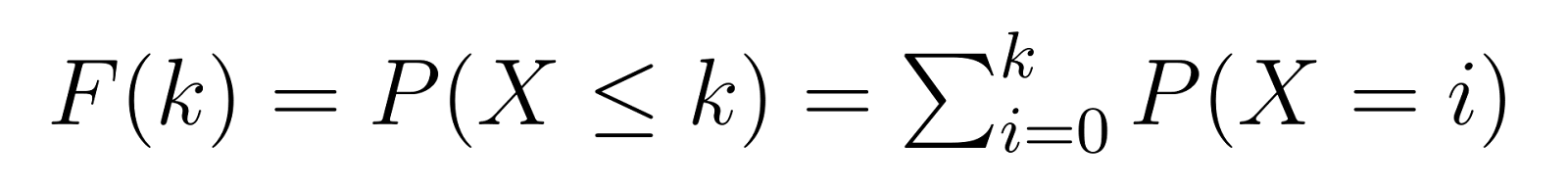
This means that F(k) gives us the probability of needing at most k non-defective units before finding our third defective one. For example, F(5) would give us the probability of needing 5 or fewer non-defective units.
Mean and variance
The mean (expected value) and variance of the negative binomial distribution have elegant formulas that reveal important properties about the mean (μ) and variance (σ²).
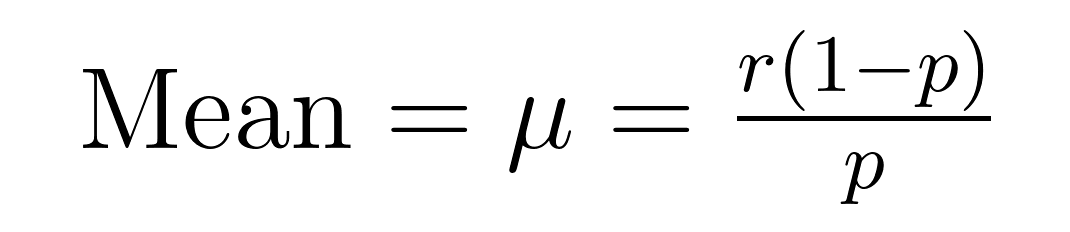
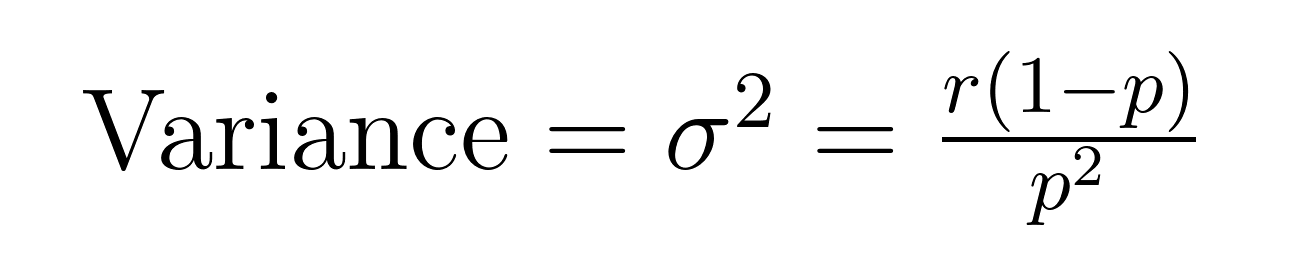
These formulas demonstrate why this distribution excels at modeling overdispersed data. Notice that the variance is always larger than the mean by a factor of 1/p. This built-in property makes it naturally suited for datasets where variability exceeds the average.
For example, if we’re modeling customer service calls where we expect to resolve 5 cases (r = 5) with a 20% success rate per attempt (p = 0.2), the expected number of failed attempts would be:
- Mean = 5(1-0.2)/0.2 = 20 failures
- Variance = 5(1-0.2)/0.2² = 100
This higher variance accounts for the reality that some cases might be resolved quickly while others require many more attempts, a pattern often observed in real-world scenarios.
Understanding these characteristics helps us recognize when to apply the negative binomial distribution and how to interpret its results effectively. These mathematical foundations set the stage for practical applications and implementation, which we’ll explore in subsequent sections.
Implementation in Python and R
Let’s validate our earlier example: calculating the probability of getting exactly 5 non-defective units before finding the third defective one (r=3, p=0.1).
Python implementation
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # Calculate binomial coefficient (k+r-1 choose k) binom_coef = math.comb(k + r - 1, k) # Calculate p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # Our example parameters k = 5 # failures (non-defective units) r = 3 # successes (defective units) p = 0.1 # probability of success (defective) # Calculate using our function prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # Verify using scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
The above code snippet should output the below:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R implementation
# Calculate probability mass function k <- 5 # failures (non-defective units) r <- 3 # successes (defective units) p <- 0.1 # probability of success (defective) # Using dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # Manual calculation for verification manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
The above code snippet should output the same numbers as from our Python example:
R calculation: 0.0124 Manual Calculation: 0.0124
Both implementations confirm our earlier calculated probability of approximately 0.0124 or 1.24%.
Relation to Other Distributions
Understanding how the negative binomial distribution relates to other probability distributions helps clarify when to use each one. The negative binomial distribution has unique connections with several important distributions in statistics.
Negative binomial distribution vs. binomial distribution
The binomial distribution serves as a foundational starting point. While the binomial distribution counts successes in a fixed number of trials, the negative binomial flips this concept by counting the trials needed for a fixed number of successes. These distributions are complementary – if you need exactly 3 successes and want to know the probability of achieving this in exactly 8 trials, use the binomial distribution. If you want to know the probability of needing exactly 8 trials to get 3 successes, use the negative binomial.
Negative binomial distribution vs. Poisson distribution
The Poisson distribution is often compared to the negative binomial when modeling count data. Both handle discrete events, but they differ in their variance assumptions. The Poisson distribution’s defining characteristic is that its mean equals its variance. However, real-world count data frequently exhibits overdispersion, where the variance exceeds the mean. The negative binomial distribution naturally accommodates this extra variability, making it more suitable for phenomena like:
- Disease outbreak patterns where some cases lead to many more infections
- Customer complaint data where some issues trigger multiple related complaints
- Website traffic spikes where certain events cause elevated activity levels
Negative binomial distribution vs. geometric distribution
The geometric distribution emerges as a special case of the negative binomial when we set r=1, meaning we’re waiting for just one success. This makes it perfect for modeling scenarios like:
- Number of attempts until first success
- Time until first failure in reliability testing
- Number of trials until first breakthrough in research
Negative binomial distribution as a Gamma-Poisson mixture
Finally, the negative binomial can be derived as a Gamma-Poisson mixture, providing a theoretical foundation for its ability to handle overdispersion. This relationship helps explain why the negative binomial distribution works well in hierarchical models where individual rates of occurrence vary according to a gamma distribution.
Advantages and Limitations
The negative binomial distribution offers distinct advantages that make it valuable for modeling real-world phenomena, while also having important limitations that data scienstists should consider.
| Advantages | Limitations |
|---|---|
| Flexibly handles overdispersed data when variance exceeds mean | Requires independence between trials/events |
| Parameters have clear interpretations for practical use | Parameter estimation becomes unreliable with small samples |
| Accommodates both counts and proportions | Computationally more intensive than simpler distributions |
| Naturally models clustering in count data | May overfit when data isn’t truly overdispersed |
| Works well with time-series and longitudinal data | Assumes constant probability of success across trials |
Negative Binomial Regression
Negative binomial regression extends traditional regression to count data, particularly when the data shows overdispersion. While Poisson regression assumes the mean equals the variance, negative binomial regression relaxes this constraint, making it more suitable for real-world applications.
Consider a call center scenario: We want to predict the number of customer service calls per hour. Our predictors might include:
- Time of day
- Day of week
- Holiday status
- Marketing campaign activity
- Weather conditions
Standard Poisson regression might underestimate the variation in call volumes, especially during peak hours or special events. Negative binomial regression accounts for this extra variability, providing more realistic predictions and confidence intervals.
Conclusion
Through its ability to model complex count data and handle overdispersion, the negative binomial distribution remains an essential tool for understanding and predicting real-world phenomena. As you have seen, it excels at modeling overdispersed data, it provides flexibility to model a huge number of different scenarios, and it even naturally extends to regression analysis.
If you are interested in deepening your understanding of probability distributions and their applications, our Probability and Statistics courses offer comprehensive coverage of these topics. Our courses include hands-on exercises with real-world datasets, helping you master both theoretical concepts and practical implementations in Python and R. Also, do consider our Machine Learning Scientist in Python career track. I promise, you will learn a lot.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













