在我长达十年的量化金融之旅中,我遇到了许多统计分布,但很少有像负二项分布这样的命名既引人入胜又实用的。在分析交易模式和风险模型时,我发现这种分布,尽管其名字似乎有些悲观,却能提供对许多简单模型无法捕捉的计数过程的洞察。
负二项分布为建模这种场景提供了一个复杂的框架,比其简单的对手如泊松分布提供了更大的灵活性。它作为二项分布的自然延伸,适应了我们需要对试验次数建模直到发生一定数量事件的情况,而不是在固定次数的试验中发生事件的数量。
在这份全面指南中,我们将探讨负二项分布的数学基础、实际应用以及在Python和R中的实现。从其基本属性开始,逐步深入到高级应用,我们将建立对这一强大统计工具的全面理解。
什么是负二项分布?
负二项分布起源于18世纪对概率在机会游戏中的研究。这种离散概率分布模拟了在达到预定成功次数之前连续进行独立伯努利试验中失败的次数。每次试验必须是独立的,并且具有相同的成功概率。
为了直观地理解这种分布,可以考虑一个简单的实验:面试候选人直到找到三个合格的人选。该分布将模拟在找到这三个合格候选人(成功)之前需要进行多少次失败面试。这与二项分布有根本的区别,后者反而模拟了在固定次数的试验中获得成功的次数,比如在正好20次面试中找到合格候选人的次数。
所以你可以看到,即使“负二项式”这个名字可能会引起疑惑,它在传统意义上并不意味着任何负面含义。 “负”这个方面源自它历史推导中涉及负指数。
负二项分布的使用领域
负二项分布在许多不同领域中被使用。它在金融领域被广泛应用,这也是我最常见到它的地方,它可以模拟诸如实现目标利润水平需要的交易日数,或者在找到一定数量的合格借款人之前审查的信用申请数。
更一般地,负二项分布在建模计数数据时也被证明很有价值,特别是当方差超过均值时,这种现象被称为过度离散性。而泊松分布假设均值等于方差,真实世界的计数数据往往表现出更大的变异性。例如,在流行病学中,疾病病例数量经常比泊松模型预测的变化更大,因此负二项分布更适合用于建模疾病传播。
遗传学家在分析测序数据时依赖于这种分布。在RNA测序实验中,基因表现水平变化很大,具有很高的变异性。负二项分布模拟了映射到每个基因的序列读数,考虑到技术和生物变异。这有助于比假定恒定方差的方法更准确地识别差异表达的基因。
在生态学研究中,研究人员使用负二项分布来建模物种丰度。以研究鸟类种群为例:一些地区可能只有很少的鸟类,而其他地区可能有大量的鸟类群集,导致方差比预期的要大。负二项分布有效地模拟了这些聚集分布,帮助生态学家了解种群动态并规划保护工作。
负二项分布的特征
负二项分布的特征在于两个关键参数,这些参数决定了它的形状和行为。了解这些参数和数学表示有助于我们理解这种分布如何模拟现实世界的现象。让我们系统地探讨这些特征。
数学表示和参数
负二项分布有两个基本参数:
- r – 目标成功次数(正整数)
- p – 每次试验成功的概率(介于0和1之间)
这些参数塑造了分布的行为方式。考虑跟踪需要进行多少次销售电话才能获得五位新客户(r = 5),当每次电话成功的概率为20%(p = 0.2)时。r的值决定了我们的停止点,而p影响了我们可能需要继续拨打电话的时间。
当我们增加r但保持p恒定时,分布向右移动并变得更加分散,反映出我们需要更多次试验才能取得更多成功。相反,当我们增加p但保持r恒定时,分布向左移动并变得更加集中,表明当成功更有可能时通常需要更少的试验。
概率质量函数(PMF)和累积分布函数(CDF)
概率质量函数给出了在获得r次成功之前需要恰好k次失败的概率。对于负二项分布,概率质量函数为:
其中:
- X表示获得r次成功之前的失败次数
- (k+r-1 choose k)是二项式系数,表示排列k次失败和r-1次成功的方式数
- p是成功的概率
- r是期望的成功次数
- K是失败的次数
示例:在质量控制中,如果我们需要3个次品单位(r = 3),每个单位有10%的次品几率(p = 0.1),我们可以计算特定概率。例如,在找到第三个次品单位之前恰好获得5个非次品单位(k = 5)的概率是:
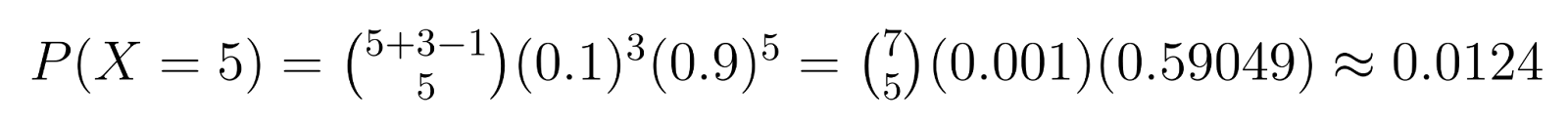
这个计算显示了在找到第三个次品单位之前恰好需要5个非次品单位的概率约为1.24%。
累积分布函数(CDF)建立在PMF基础上,给出了在实现我们的成功目标之前需要k个或更少的失败的概率:
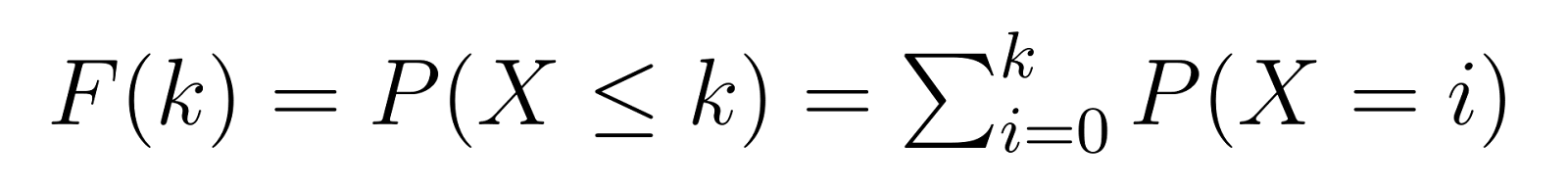
这意味着F(k)给出了在找到我们的第三个次品单位之前最多需要k个非次品单位的概率。例如,F(5)将给出我们需要5个或更少的非次品单位的概率。
均值和方差
负二项分布的均值(期望值)和方差有优雅的公式,揭示了关于均值(μ)和方差(σ²)的重要性质。
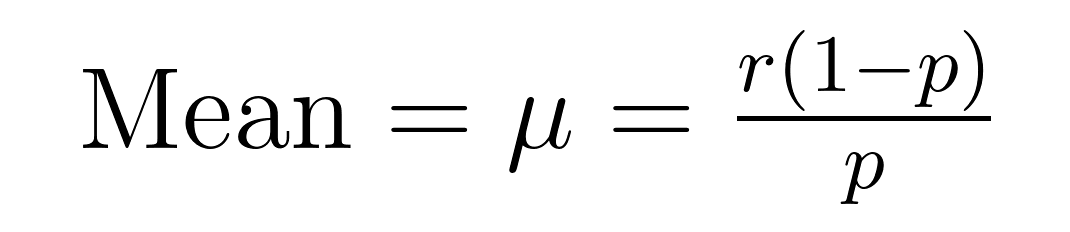
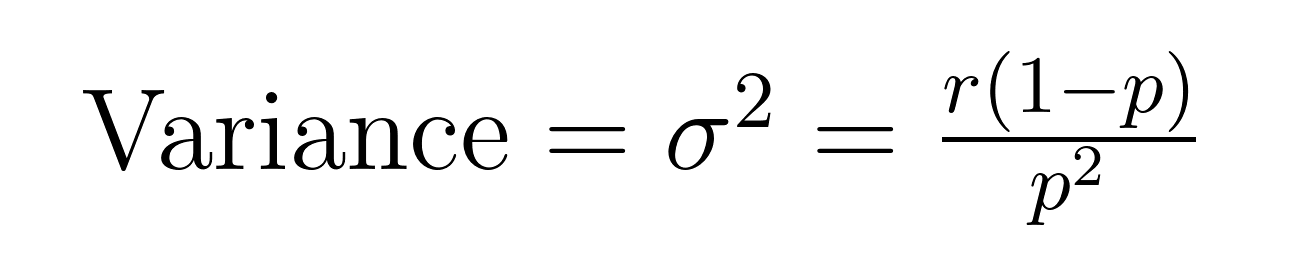
这些公式展示了为什么这个分布在建模过分散数据方面表现出色。请注意,方差始终比均值大一个1/p的因子。这一内在属性使其自然适用于变异性超过平均水平的数据集。
例如,如果我们正在建模客户服务电话,其中我们预期解决5个案例(r = 5),每次尝试的成功率为20%(p = 0.2),则预期的失败尝试次数为:
- 均值 = 5(1-0.2)/0.2 = 20 次失败
- 方差 = 5(1-0.2)/0.2² = 100
这种更高的方差说明了一种现实,即有些情况可能很快解决,而其他情况则需要更多的尝试,这种模式在现实场景中经常被观察到。
了解这些特征有助于我们识别何时应用负二项分布以及如何有效解释其结果。这些数学基础为实际应用和实施奠定了基础,我们将在后续章节中探讨。
Python和R中的实施
让我们验证之前的示例:计算在找到第三个有缺陷的单位之前恰好获得5个非有缺陷单位的概率(r=3,p=0.1)。
Python实现
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # 计算二项式系数(k+r-1 选择 k) binom_coef = math.comb(k + r - 1, k) # 计算 p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # 我们的示例参数 k = 5 # 失败次数(非缺陷单位) r = 3 # 成功次数(缺陷单位) p = 0.1 # 成功的概率(缺陷) # 使用我们的函数进行计算 prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # 使用 scipy 进行验证 prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
上述代码片段应输出如下内容:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R 实现
# 计算概率质量函数 k <- 5 # 失败次数(非缺陷单位) r <- 3 # 成功次数(缺陷单位) p <- 0.1 # 成功的概率(缺陷) # 使用 dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # 手动计算以进行验证 manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
上面的代码片段应该输出与我们的Python示例中相同的数字:
R calculation: 0.0124 Manual Calculation: 0.0124
这两种实现都证实了我们之前计算的概率约为0.0124或1.24%。
与其他分布的关系
了解负二项分布与其他概率分布的关系有助于澄清何时使用每种分布。负二项分布与统计学中几个重要分布有独特的联系。
负二项分布与二项分布
二项分布是一个基础起点。而负二项分布则通过计算达到固定成功次数所需的试验次数来颠覆这一概念。这些分布是互补的 – 如果你需要确切地3次成功,并想知道在恰好8次试验中实现这一点的概率,使用二项分布。如果你想知道需要恰好8次试验才能获得3次成功的概率,则使用负二项分布。
负二项分布 vs. 泊松分布
当建模计数数据时,泊松分布经常与负二项分布进行比较。它们都处理离散事件,但它们在方差假设上有所不同。泊松分布的定义特征是其均值等于方差。然而,现实世界中的计数数据经常表现出过度离散,即方差超过均值。负二项分布自然地适应了这种额外的变异性,使其更适用于诸如:
- 一些病例导致更多感染的疾病爆发模式
- 客户投诉数据,其中一些问题会触发多个相关投诉
- 网站流量激增,某些事件会导致活动水平提高
负二项分布与几何分布
当我们设定 r=1 时,几何分布会出现作为负二项分布的特例,这意味着我们只等待一个成功。这使其非常适合建模以下场景:
- 直到第一次成功的尝试次数
- 可靠性测试中第一次失败的时间
- 研究中第一次突破的尝试次数
负二项分布作为Gamma-Poisson混合
最终,负二项分布可以推导为Gamma-Poisson混合,为其处理过度离散性能力提供了理论基础。这种关系有助于解释为什么负二项分布在层次模型中效果很好,其中个体发生率根据Gamma分布而变化。
优势和局限
负二项分布提供了明显优势,使其对建模现实世界现象非常有价值,同时也具有数据科学家应考虑的重要局限。
| Advantages | Limitations |
|---|---|
| 在方差超过均值时灵活处理过度离散数据 | 需要试验/事件之间的独立性 |
| 参数在实际使用中具有清晰的解释 | 参数估计在样本较小时变得不可靠 |
| 适用于计数和比例 | 计算比较精细的分布更加耗时 |
| 自然模拟计数数据中的聚类 | 当数据并非真正过度离散时可能过拟合 |
| 在时间序列和纵向数据中表现良好 | 假设各次试验中成功的概率恒定 |
负二项回归
负二项回归将传统回归扩展到计数数据,特别是在数据表现出过度离散时。虽然泊松回归假设均值等于方差,但负二项回归放宽了这一限制,使其更适合实际应用。
考虑一个呼叫中心的场景:我们想预测每小时的客户服务电话数量。我们的预测变量可能包括:
- 一天中的时间
- 星期几
- 假期状态
- 营销活动情况
- 天气条件
标准泊松回归可能会低估呼叫量的变化,特别是在高峰时段或特殊事件期间。负二项回归考虑了这种额外的变异性,提供了更现实的预测和置信区间。
结论
通过其对复杂计数数据的建模能力和处理过度离散性,负二项分布仍然是理解和预测现实现象的重要工具。正如您所见,它在建模过度离散数据方面表现出色,为模拟大量不同场景提供了灵活性,甚至自然延伸到回归分析。
如果您对加深对概率分布及其应用的了解感兴趣,我们的概率与统计课程涵盖了这些主题的全面内容。我们的课程包括与真实数据集进行的动手练习,帮助您掌握Python和R中的理论概念和实际应用。此外,请考虑我们的Python机器学习科学家职业专业方向。我保证,您会学到很多。
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













