В течение десятилетнего пути в области количественной финансовой деятельности я столкнулся с множеством статистических распределений, но немногие оказались столь же увлекательно названными, но при этом практически ценными, как отрицательное биномиальное распределение. Анализируя торговые паттерны и модели риска, я обнаружил, что это распределение, несмотря на свое кажущееся пессимистическое название, предлагает понимание счетных процессов, которые многие более простые модели не улавливают.
Отрицательное биномиальное распределение предоставляет сложную структуру для моделирования таких сценариев, предлагая большую гибкость по сравнению с более простыми аналогами, такими как распределение Пуассона. Оно служит естественным продолжением биномиального распределения, приспосабливаясь к ситуациям, когда нам нужно моделировать количество испытаний до наступления определенного числа событий, а не количество событий в фиксированном количестве испытаний.
В данном исчерпывающем руководстве мы исследуем математические основы отрицательного биномиального распределения, его практические применения и реализацию в Python и R. Начиная с его основных свойств и переходя к продвинутым применениям, мы построим полное понимание этого мощного статистического инструмента.
Что такое отрицательное биномиальное распределение?
Негативное биномиальное распределение возникло в 18 веке в результате изучения вероятности в азартных играх. Это дискретное распределение вероятностей моделирует количество неудач в последовательности независимых бернуллиевских испытаний до достижения заранее определенного количества успехов. Каждое испытание должно быть независимым и иметь одинаковую вероятность успеха.
Чтобы интуитивно понять это распределение, рассмотрим простой эксперимент: собеседование с кандидатами до тех пор, пока не будут найдены три квалифицированных кандидата на должность. Распределение будет моделировать количество неудачных собеседований (неудач), необходимых для нахождения этих трех квалифицированных кандидатов (успехов). Это принципиально отличается от биномиального распределения, которое вместо этого моделирует количество успехов в фиксированном числе испытаний – например, количество квалифицированных кандидатов, найденных в exactly 20 собеседованиях.
Как видите, хотя название “отрицательное биномиальное” может вызвать недоумение, это не подразумевает ничего отрицательного в обычном смысле. Аспект “отрицательный” происходит из его исторического происхождения, включающего отрицательные показатели.
Где используется отрицательное биномиальное распределение
Отрицательное биномиальное распределение используется различными способами. Оно используется в финансах, где я его чаще всего встречаю, где моделирует сценарии, такие как количество торговых дней до достижения целевого уровня прибыли или количество рассмотренных кредитных заявок перед обнаружением определенного числа квалифицированных заемщиков.
В более общем смысле, отрицательное биномиальное распределение также оказалось полезным для моделирования счетных данных, когда дисперсия превышает среднее значение, явление, известное как овердисперсия. В то время как распределение Пуассона предполагает, что среднее равно дисперсии, реальные счетные данные часто демонстрируют большую изменчивость. Например, в эпидемиологии количество случаев заболеваний часто варьируется больше, чем предсказывает модель Пуассона, что делает отрицательное биномиальное распределение более подходящим для моделирования распространения заболеваний.
Генетики полагаются на это распределение при анализе данных секвенирования. В экспериментах по секвенированию РНК гены показывают различные уровни экспрессии с высокой изменчивостью. Отрицательное биномиальное распределение моделирует количество считываний последовательностей, сопоставленных с каждым геном, учитывая как техническую, так и биологическую вариацию. Это помогает более точно идентифицировать дифференциально экспрессируемые гены, чем методы, предполагающие постоянную дисперсию.
В экологических исследованиях исследователи используют его для моделирования изобилия видов. Рассмотрим изучение популяций птиц: некоторые районы могут иметь мало птиц, в то время как в других образуются большие скопления, создавая более высокую дисперсию, чем ожидалось. Отрицательное биномиальное распределение эффективно моделирует эти скопления, помогая экологам понять динамику популяции и планировать усилия по сохранению.
Характеристики отрицательного биномиального распределения
Отрицательное биномиальное распределение характеризуется двумя основными параметрами, определяющими его форму и поведение. Понимание этих параметров и математического представления помогает нам понять, как это распределение моделирует явления реального мира. Давайте систематически исследуем эти характеристики.
Математическое представление и параметры
Отрицательное биномиальное распределение имеет два фундаментальных параметра:
- r – Целевое количество успехов (положительное целое число)
- p – Вероятность успеха в каждой попытке (между 0 и 1)
Эти параметры определяют поведение распределения. Представьте, что вы отслеживаете количество звонков для заключения пяти новых клиентов (r = 5), когда вероятность успеха в каждом звонке составляет 20% (p = 0.2). Значение r определяет нашу точку остановки, а p влияет на то, как долго мы можем ожидать продолжать звонки.
Когда мы увеличиваем r, оставляя p постоянным, распределение смещается вправо и становится более разбросанным, отражая то, что нам нужно больше попыток для достижения успехов. Напротив, когда мы увеличиваем p, оставляя r постоянным, распределение смещается влево и становится более концентрированным, указывая на то, что typично требуется меньше попыток, когда вероятность успеха выше.
Функция вероятности (PMF) и кумулятивная функция распределения (CDF)
Функция вероятности массы дает нам вероятность того, что нам понадобится ровно k неудач перед достижением r успехов. Для отрицательного биномиального распределения ФВМ выглядит следующим образом:
Где:
- X представляет собой количество неудач перед достижением r успехов
- (k+r-1 выбрать k) является биномиальным коэффициентом, представляющим количество способов упорядочить k неудач и r-1 успех
- p – вероятность успеха
- r – желаемое количество успехов
- K – количество неудач
Пример: В контроле качества, если нам нужно 3 дефектных блока (r = 3) и каждый блок имеет вероятность 10% быть дефектным (p = 0.1), мы можем рассчитать конкретные вероятности. Например, вероятность получить ровно 5 недефектных блоков (k = 5) до обнаружения третьего дефектного блока:
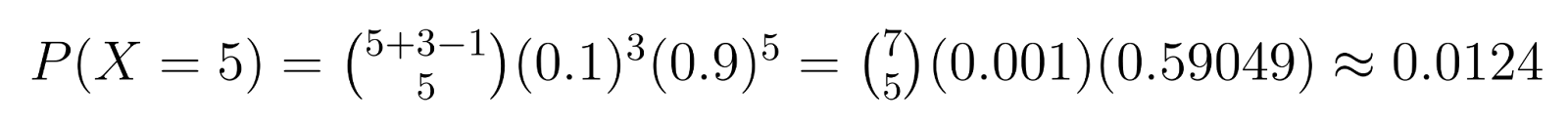
Этот расчет показывает вероятность около 1.24% того, что понадобится ровно 5 недефектных блоков до обнаружения третьего дефектного.
Функция кумулятивного распределения (CDF) базируется на PMF, давая нам вероятность требования k или менее неудач перед достижением нашей целевой численности успехов:
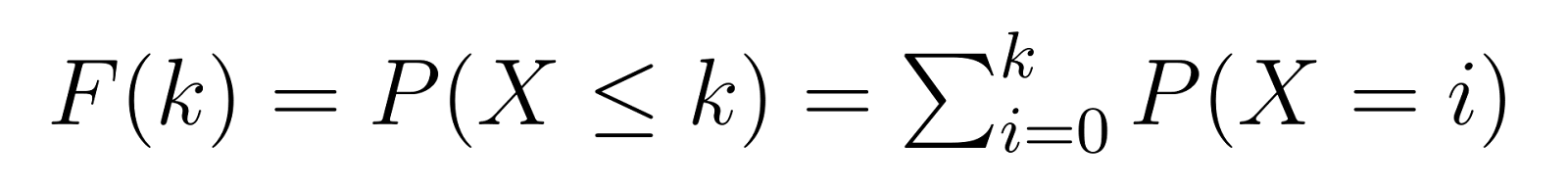
Это означает, что F(k) дает нам вероятность понадобиться не более k недефектных блоков до обнаружения третьего дефектного. Например, F(5) дало бы нам вероятность понадобиться 5 или менее недефектных блоков.
Среднее и дисперсия
Среднее (ожидаемое значение) и дисперсия отрицательного биномиального распределения имеют элегантные формулы, которые раскрывают важные свойства о среднем (μ) и дисперсии (σ²).
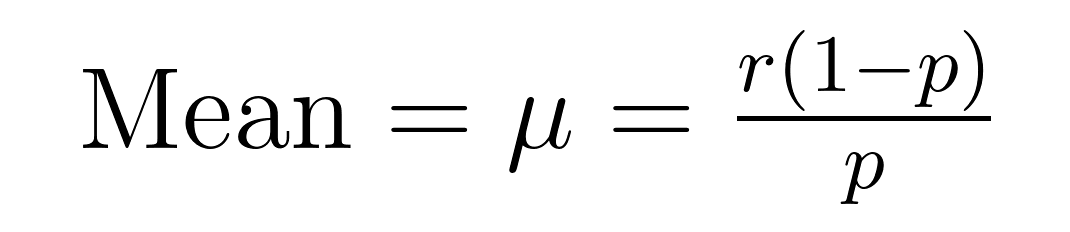
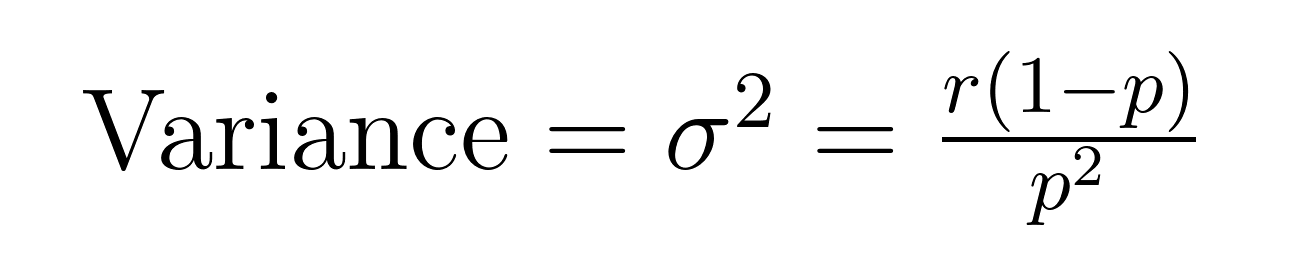
Эти формулы демонстрируют, почему это распределение отлично подходит для моделирования избыточных данных. Обратите внимание, что дисперсия всегда больше среднего на величину 1/p. Это встроенное свойство делает его естественно подходящим для наборов данных, где изменчивость превышает среднее значение.
Например, если мы моделируем звонки в службу поддержки, где мы ожидаем разрешить 5 случаев (r = 5) с вероятностью успеха в 20% за попытку (p = 0.2), ожидаемое количество неудачных попыток будет:
- Среднее = 5(1-0.2)/0.2 = 20 неудач
- Дисперсия = 5(1-0.2)/0.2² = 100
Этот более высокий разброс объясняет тот факт, что некоторые случаи могут быть быстро решены, в то время как другие требуют гораздо большего количества попыток, что часто наблюдается в реальных сценариях.
Понимание этих характеристик помогает нам понять, когда применять отрицательное биномиальное распределение и как эффективно интерпретировать его результаты. Эти математические основы создают основу для практических применений и реализации, которые мы рассмотрим в последующих разделах.
Реализация на Python и R
Давайте проверим наш пример: расчет вероятности получить ровно 5 некондиционных единиц до обнаружения третьей дефектной (r=3, p=0.1).
Реализация на Python
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # Вычислить биномиальный коэффициент (k+r-1 выбрать k) binom_coef = math.comb(k + r - 1, k) # Вычислить p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # Наши примеры параметров k = 5 # неудачи (не дефектные единицы) r = 3 # успехи (дефектные единицы) p = 0.1 # вероятность успеха (дефектное) # Вычислить, используя нашу функцию prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # Проверить, используя scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
Приведенный выше фрагмент кода должен вывести следующее:
Manual calculation: 0.0124 SciPy calculation: 0.0124
R-реализация
# Вычислить функцию вероятности массы k <- 5 # неудачи (не дефектные единицы) r <- 3 # успехи (дефектные единицы) p <- 0.1 # вероятность успеха (дефектное) # Используя dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # Ручной расчет для проверки manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
Вышеуказанный фрагмент кода должен выводить те же числа, что и наш пример на Python:
R calculation: 0.0124 Manual Calculation: 0.0124
Обе реализации подтверждают наш ранее вычисленный результат вероятности примерно 0.0124 или 1.24%.
Связь с другими распределениями
Понимание того, как отрицательное биномиальное распределение связано с другими распределениями вероятностей, помогает прояснить, когда использовать каждое из них. Отрицательное биномиальное распределение имеет уникальные связи с несколькими важными распределениями в статистике.
Отрицательное биномиальное распределение против биномиального распределения
Биномиальное распределение служит основой для начала. В то время как биномиальное распределение считает успехи в фиксированном числе испытаний, негативное биномиальное распределение переворачивает эту концепцию, подсчитывая испытания, необходимые для достижения фиксированного числа успехов. Эти распределения являются взаимодополняющими – если вам нужно ровно 3 успеха и вы хотите знать вероятность достижения этого в ровно 8 испытаниях, используйте биномиальное распределение. Если вы хотите знать вероятность необходимости ровно 8 испытаний для получения 3 успехов, используйте негативное биномиальное распределение.
Негативное биномиальное распределение против распределения Пуассона
Распределение Пуассона часто сравнивают с негативным биномиальным при моделировании счетных данных. Оба обрабатывают дискретные события, но они отличаются по своим предположениям о дисперсии. Определяющей характеристикой распределения Пуассона является то, что его среднее равно его дисперсии. Однако реальные счетные данные часто демонстрируют переизбыточность, когда дисперсия превышает среднее. Негативное биномиальное распределение естественно учитывает эту дополнительную изменчивость, что делает его более подходящим для таких явлений, как:
- Шаблоны вспышек заболеваний, где некоторые случаи приводят к многим другим инфекциям
- Данные о жалобах клиентов, где некоторые проблемы вызывают несколько связанных жалоб
- Всплески трафика на веб-сайте, когда определенные события вызывают повышенный уровень активности
Отрицательное биномиальное распределение против геометрического распределения
Геометрическое распределение возникает как частный случай отрицательного биномиального распределения, когда мы устанавливаем r=1, что означает, что мы ждем только одного успеха. Это делает его идеальным для моделирования сценариев, таких как:
- Количество попыток до первого успеха
- Время до первого отказа при надежностном тестировании
- Количество испытаний до первого прорыва в исследованиях
Отрицательное биномиальное распределение как смесь гамма-Пуассона
В конечном итоге, отрицательное биномиальное распределение может быть выведено как смесь гамма-Пуассона, что обеспечивает теоретическую основу для его способности справляться с переизбытком. Эта связь помогает объяснить, почему отрицательное биномиальное распределение хорошо работает в иерархических моделях, где индивидуальные rates частоты варьируются в соответствии с гамма-распределением.
Преимущества и ограничения
Отрицательное биномиальное распределение предлагает явные преимущества, которые делают его ценным для моделирования реальных явлений, но также имеет важные ограничения, которые должны учитывать специалисты по данным.
| Advantages | Limitations |
|---|---|
| Гибко обрабатывает переизбыточные данные, когда дисперсия превышает среднее | Требует независимости между испытаниями/событиями |
| Параметры имеют ясные интерпретации для практического использования | Оценка параметров становится ненадежной при малых выборках |
| Учитывает как частоты, так и пропорции | Вычислительно более интенсивно, чем более простые распределения |
| Естественно моделирует кластеризацию в данных о подсчетах | Может переобучиться, когда данные не являются действительно переизбыточными |
| Хорошо работает с временными рядами и продольными данными | Предполагает постоянную вероятность успеха в испытаниях |
Отрицательная биномиальная регрессия
Отрицательная биномиальная регрессия расширяет традиционную регрессию на данные счетчика, особенно когда данные показывают избыточность. В то время как Пуассоновская регрессия предполагает, что среднее равно дисперсии, отрицательная биномиальная регрессия смягчает это ограничение, что делает ее более подходящей для прикладных задач в реальном мире.
Представьте себе сценарий колл-центра: мы хотим предсказать количество звонков в службу поддержки клиентов в час. Наши предикторы могут включать:
- Время суток
- День недели
- Статус праздника
- Активность маркетинговой кампании
- Погодные условия
Стандартная регрессия Пуассона может недооценивать изменчивость объема звонков, особенно в пиковые часы или во время специальных мероприятий. Регрессия отрицательного биномиального распределения учитывает эту дополнительную изменчивость, обеспечивая более реалистичные прогнозы и доверительные интервалы.
Заключение
Благодаря своей способности моделировать сложные данные о количестве и справляться с избыточностью, отрицательное биномиальное распределение остается важным инструментом для понимания и прогнозирования явлений реального мира. Как вы видели, оно отлично подходит для моделирования избыточных данных, обладает гибкостью для моделирования огромного количества различных сценариев и даже естественным образом расширяется до регрессионного анализа.
Если вас интересует углубленное понимание вероятностных распределений и их применение, наши курсы Теория вероятностей и статистика предлагают всестороннее изучение этих тем. Наши курсы включают практические упражнения с реальными наборами данных, помогая вам овладеть как теоретическими концепциями, так и практическими реализациями на Python и R. Также обратите внимание на нашу программу Машинное обучение на языке Python. Обещаю, вы узнаете много.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













