Dans mon parcours décennal en finance quantitative, j’ai rencontré de nombreuses distributions statistiques, mais peu se sont révélées aussi intrigantes par leur nom et pourtant aussi précieuses en pratique que la distribution binomiale négative. En analysant les modèles de trading et les modèles de risque, j’ai découvert que cette distribution, malgré son nom en apparence pessimiste, offre des insights sur les processus de comptage que de nombreux modèles plus simples échouent à capturer.
La distribution binomiale négative fournit un cadre sophistiqué pour modéliser de tels scénarios, offrant une plus grande flexibilité que ses homologues plus simples comme la distribution de Poisson. Elle sert d’extension naturelle de la distribution binomiale, s’adaptant aux situations où nous devons modéliser le nombre d’essais jusqu’à ce qu’un certain nombre d’événements se produisent, plutôt que le nombre d’événements dans un nombre fixe d’essais.
Dans ce guide complet, nous explorerons les fondations mathématiques de la distribution binomiale négative, ses applications pratiques et sa mise en œuvre en Python et R. En partant de ses propriétés de base et en passant aux applications avancées, nous construirons une compréhension approfondie de cet outil statistique puissant.
Qu’est-ce que la distribution binomiale négative ?
La distribution binomiale négative a été initiée au 18ème siècle à travers l’étude de la probabilité dans les jeux de hasard. Cette distribution de probabilité discrète modélise le nombre d’échecs dans une séquence de essais de Bernoulli indépendants avant d’atteindre un nombre prédéterminé de succès. Chaque essai doit être indépendant et avoir la même probabilité de succès.
Pour comprendre intuitivement cette distribution, considérons une expérience simple : interviewer des candidats jusqu’à trouver trois personnes qualifiées pour un poste. La distribution modéliserait le nombre d’entretiens infructueux (échecs) nécessaires avant de trouver ces trois candidats qualifiés (succès). Cela diffère fondamentalement de la distribution binomiale, qui modélise plutôt le nombre de succès dans un nombre fixe d’essais – comme le nombre de candidats qualifiés trouvés exactement lors de 20 entretiens.
Vous pouvez donc voir que même si le nom « binomiale négative » peut surprendre, il n’implique rien de négatif au sens conventionnel. L’aspect « négatif » provient de sa dérivation historique impliquant des exposants négatifs.
Où la distribution binomiale négative est utilisée
La distribution binomiale négative est utilisée de différentes manières. Elle est utilisée en finance, où je la place le plus souvent, où elle modélise des scénarios tels que le nombre de jours de négociation jusqu’à l’atteinte d’un niveau de profit cible, ou le nombre de demandes de crédit examinées avant de trouver un certain nombre d’emprunteurs qualifiés.
Plus généralement, la distribution binomiale négative s’est également avérée utile pour modéliser des données de dénombrement lorsque la variance dépasse la moyenne, un phénomène connu sous le nom de surdispersion. Alors que la distribution de Poisson suppose que la moyenne égale la variance, les données de dénombrement du monde réel montrent souvent une plus grande variabilité. Par exemple, en épidémiologie, le nombre de cas de maladie varie souvent plus que ce que prédirait un modèle de Poisson, ce qui rend la distribution binomiale négative plus appropriée pour modéliser la propagation de la maladie.
Les généticiens se fient à cette distribution lors de l’analyse de données de séquençage. Dans les expériences de séquençage d’ARN, les gènes montrent des niveaux d’expression variables avec une forte variabilité. La distribution binomiale négative modélise le nombre de lectures de séquence associées à chaque gène, tenant compte à la fois de la variation technique et biologique. Cela permet d’identifier les gènes différentiellement exprimés de manière plus précise que les méthodes supposant une variance constante.
Dans les études écologiques, les chercheurs l’utilisent pour modéliser l’abondance des espèces. Considérons l’étude des populations d’oiseaux : certaines zones peuvent avoir peu d’oiseaux tandis que d’autres ont de grands regroupements, créant une variance plus élevée que prévu. La binomiale négative modélise efficacement ces distributions regroupées, aidant les écologistes à comprendre la dynamique des populations et à planifier des efforts de conservation.
Caractéristiques de la distribution binomiale négative
La distribution binomiale négative est caractérisée par deux paramètres clés qui déterminent sa forme et son comportement. Comprendre ces paramètres et la représentation mathématique nous aide à saisir comment cette distribution modélise les phénomènes du monde réel. Explorons ces caractéristiques de manière systématique.
Représentation mathématique et paramètres
La distribution binomiale négative a deux paramètres fondamentaux :
- r – Le nombre cible de succès (un entier positif)
- p – La probabilité de succès à chaque essai (entre 0 et 1)
Ces paramètres déterminent le comportement de la distribution. Considérez le suivi du nombre d’appels de vente nécessaires pour obtenir cinq nouveaux clients (r = 5) lorsque chaque appel a une chance de succès de 20% (p = 0,2). La valeur de r détermine notre point d’arrêt, tandis que p influence la durée pendant laquelle nous pouvons nous attendre à continuer à passer des appels.
Lorsque nous augmentons r tout en gardant p constant, la distribution se déplace vers la droite et devient plus étalée, ce qui reflète le fait que nous avons besoin de plus d’essais pour obtenir plus de succès. En revanche, lorsque nous augmentons p tout en gardant r constant, la distribution se déplace vers la gauche et devient plus concentrée, indiquant que moins d’essais sont généralement nécessaires lorsque le succès est plus probable.
Fonction de masse de probabilité (PMF) et fonction de distribution cumulative (CDF)
La fonction de masse de probabilité nous donne la probabilité d’avoir exactement k échecs avant d’obtenir r succès. Pour la distribution binomiale négative, la FMP est :
Où :
- X représente le nombre d’échecs avant d’obtenir r succès
- (k+r-1 choisis k) est le coefficient binomial, représentant le nombre de façons d’arranger k échecs et r-1 succès
- p est la probabilité de succès
- r est le nombre de succès désiré
- K est le nombre d’échecs
Par exemple : En contrôle qualité, si nous avons besoin de 3 unités défectueuses (r = 3) et que chaque unité a 10% de chances d’être défectueuse (p = 0,1), nous pouvons calculer des probabilités spécifiques. Par exemple, la probabilité d’obtenir exactement 5 unités non défectueuses (k = 5) avant de trouver la troisième défectueuse est :
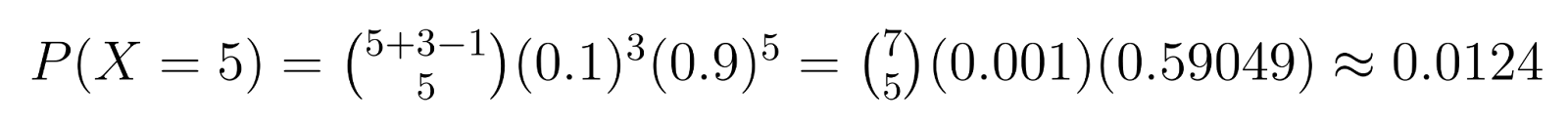
Ce calcul montre qu’il y a environ 1,24% de chances d’avoir besoin exactement de 5 unités non défectueuses avant de trouver la troisième défectueuse.
La fonction de distribution cumulative (CDF) se base sur la PMF, nous donnant la probabilité de nécessiter k ou moins d’échecs avant d’atteindre notre nombre cible de succès :
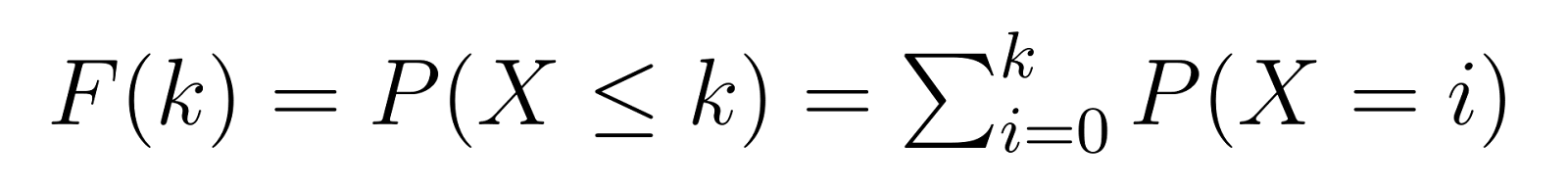
Cela signifie que F(k) nous donne la probabilité d’avoir besoin d’au plus k unités non défectueuses avant de trouver notre troisième unité défectueuse. Par exemple, F(5) nous donnerait la probabilité d’avoir besoin de 5 unités non défectueuses ou moins.
Moyenne et variance
La moyenne (valeur attendue) et la variance de la distribution binomiale négative ont des formules élégantes qui révèlent des propriétés importantes sur la moyenne (μ) et la variance (σ²).
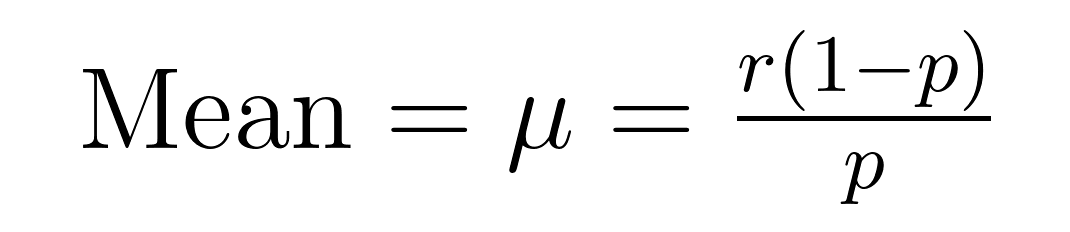
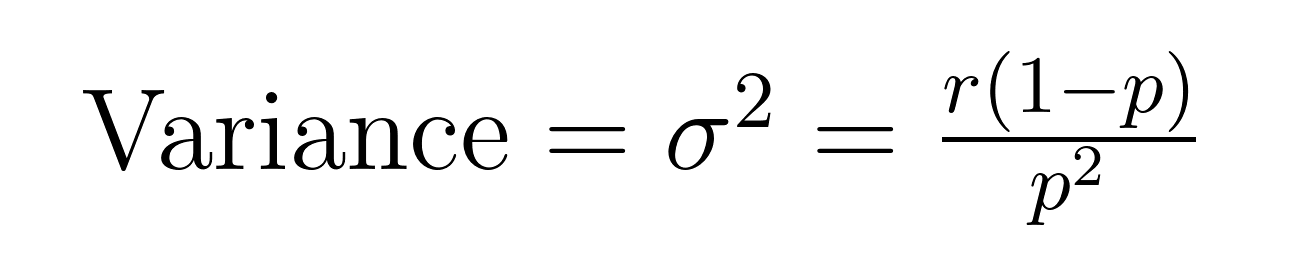
Ces formules démontrent pourquoi cette distribution excelle dans la modélisation de données surdispersées. Remarquez que la variance est toujours plus grande que la moyenne d’un facteur de 1/p. Cette propriété intégrée la rend naturellement adaptée aux ensembles de données où la variabilité dépasse la moyenne.
Par exemple, si nous modélisons les appels au service client où nous prévoyons de résoudre 5 cas (r = 5) avec un taux de réussite de 20% par tentative (p = 0,2), le nombre attendu d’échecs serait :
- Moyenne = 5(1-0.2)/0.2 = 20 échecs
- Variance = 5(1-0.2)/0.2² = 100
Cette variance plus élevée explique le fait que certains cas peuvent être résolus rapidement tandis que d’autres nécessitent beaucoup plus de tentatives, un schéma souvent observé dans des scénarios réels.
Comprendre ces caractéristiques nous aide à reconnaître quand appliquer la distribution binomiale négative et comment interpréter ses résultats de manière efficace. Ces fondements mathématiques préparent le terrain pour des applications pratiques et leur mise en œuvre, que nous explorerons dans les sections suivantes.
Mise en œuvre en Python et R
Validons notre exemple précédent : calculer la probabilité d’obtenir exactement 5 unités non défectueuses avant de trouver la troisième défectueuse (r=3, p=0.1).
Implémentation en Python
import scipy.stats as stats import math def calculate_nb_pmf(k, r, p): # Calculer le coefficient binomial (k+r-1 choisissez k) binom_coef = math.comb(k + r - 1, k) # Calculer p^r * (1-p)^k prob = (p ** r) * ((1 - p) ** k) return binom_coef * prob # Nos paramètres d'exemple k = 5 # échecs (unités non défectueuses) r = 3 # succès (unités défectueuses) p = 0.1 # probabilité de succès (défectueux) # Calculer en utilisant notre fonction prob_manual = calculate_nb_pmf(k, r, p) print(f"Manual calculation: {prob_manual:.4f}") # Vérifier en utilisant scipy prob_scipy = stats.nbinom.pmf(k, r, p) print(f"SciPy calculation: {prob_scipy:.4f}")
Le snippet de code ci-dessus devrait afficher ce qui suit:
Manual calculation: 0.0124 SciPy calculation: 0.0124
Implémentation R
# Calculer la fonction de masse de probabilité k <- 5 # échecs (unités non défectueuses) r <- 3 # succès (unités défectueuses) p <- 0.1 # probabilité de succès (défectueux) # Utilisation de dnbinom prob_r <- dnbinom(k, size = r, prob = p) print(sprintf("R calculation: %.4f", prob_r)) # Calcul manuel pour vérification manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k print(sprintf("Manual calculation: %.4f", manual_calc))
Le snippet de code ci-dessus devrait produire les mêmes nombres que notre exemple en Python :
R calculation: 0.0124 Manual Calculation: 0.0124
Les deux implémentations confirment notre probabilité calculée précédemment d’environ 0,0124 ou 1,24 %.
Relation avec d’autres distributions
Comprendre comment la distribution binomiale négative se rapporte à d’autres distributions de probabilité aide à clarifier quand utiliser chacune d’entre elles. La distribution binomiale négative a des connexions uniques avec plusieurs distributions importantes en statistiques.
Distribution binomiale négative vs distribution binomiale
La distribution binomiale sert de point de départ fondamental. Alors que la distribution binomiale compte les succès dans un nombre fixe d’essais, la binomiale négative inverse ce concept en comptant les essais nécessaires pour un nombre fixe de succès. Ces distributions sont complémentaires – si vous avez besoin exactement de 3 succès et que vous voulez connaître la probabilité d’y parvenir exactement en 8 essais, utilisez la distribution binomiale. Si vous voulez connaître la probabilité d’avoir besoin exactement de 8 essais pour obtenir 3 succès, utilisez la distribution binomiale négative.
Distribution binomiale négative vs distribution de Poisson
La distribution de Poisson est souvent comparée à la distribution binomiale négative lors de la modélisation des données de comptage. Les deux gèrent des événements discrets, mais diffèrent dans leurs hypothèses de variance. La caractéristique déterminante de la distribution de Poisson est que sa moyenne est égale à sa variance. Cependant, les données réelles de comptage présentent fréquemment une surdispersion, où la variance dépasse la moyenne. La distribution binomiale négative prend naturellement en compte cette variabilité supplémentaire, la rendant plus adaptée pour des phénomènes tels que :
- Modèles de propagation de maladies où certains cas entraînent beaucoup plus d’infections
- Données de plaintes de clients où certains problèmes déclenchent plusieurs plaintes connexes
- Fluctuations du trafic sur le site Web où certains événements provoquent des niveaux d’activité élevés
Distribution binomiale négative vs distribution géométrique
La distribution géométrique émerge comme un cas particulier de la distribution binomiale négative lorsque nous fixons r=1, ce qui signifie que nous attendons juste un succès. Cela la rend parfaite pour modéliser des scénarios tels que :
- Nombre de tentatives jusqu’au premier succès
- Temps jusqu’à la première défaillance dans les tests de fiabilité
- Nombre d’essais jusqu’à la première percée dans la recherche
Distribution binomiale négative comme un mélange Gamma-Poisson
Enfin, la distribution binomiale négative peut être dérivée comme un mélange Gamma-Poisson, fournissant une base théorique pour sa capacité à gérer la surdispersion. Cette relation aide à expliquer pourquoi la distribution binomiale négative fonctionne bien dans les modèles hiérarchiques où les taux d’occurrence individuels varient selon une distribution gamma.
Avantages et limitations
La distribution binomiale négative offre des avantages distincts qui la rendent précieuse pour modéliser des phénomènes du monde réel, tout en ayant également des limitations importantes que les scientifiques des données devraient considérer.
| Advantages | Limitations |
|---|---|
| Gère de manière flexible les données surdispersées lorsque la variance dépasse la moyenne | Nécessite l’indépendance entre les essais/événements |
| Les paramètres ont des interprétations claires pour une utilisation pratique | L’estimation des paramètres devient peu fiable avec de petits échantillons |
| Accommode à la fois les comptes et les proportions | Plus intensif computationnellement que les distributions plus simples |
| Modélise naturellement le regroupement dans les données de comptage | Peut surajuster lorsque les données ne sont pas réellement surdispersées |
| Fonctionne bien avec des données de séries temporelles et longitudinales | Suppose une probabilité de succès constante à travers les essais |
Régression binomiale négative
La régression binomiale négative étend la régression traditionnelle aux données de comptage, particulièrement lorsque les données présentent une surdispersion. Alors que la régression de Poisson suppose que la moyenne est égale à la variance, la régression binomiale négative assouplit cette contrainte, la rendant plus adaptée aux applications du monde réel.
Considérons un scénario de centre d’appels : nous voulons prédire le nombre d’appels de service client par heure. Nos prédicteurs pourraient inclure :
- Heure de la journée
- Jour de la semaine
- Statut de jour férié
- Activité de campagne marketing
- Conditions météorologiques
La régression de Poisson standard pourrait sous-estimer la variation des volumes d’appels, en particulier pendant les heures de pointe ou les événements spéciaux. La régression binomiale négative tient compte de cette variabilité supplémentaire, offrant des prédictions et des intervalles de confiance plus réalistes.
Conclusion
Grâce à sa capacité à modéliser des données de comptage complexes et à gérer la surdispersion, la distribution binomiale négative reste un outil essentiel pour comprendre et prédire les phénomènes du monde réel. Comme vous l’avez vu, elle excelle dans la modélisation de données surdispersées, elle offre la flexibilité de modéliser un grand nombre de scénarios différents, et elle s’étend même naturellement à l’analyse de régression.
Si vous êtes intéressé par approfondir votre compréhension des distributions de probabilité et de leurs applications, nos cours de Probabilité et Statistiques offrent une couverture complète de ces sujets. Nos cours comprennent des exercices pratiques avec des ensembles de données du monde réel, vous aidant à maîtriser à la fois les concepts théoriques et les mises en œuvre pratiques en Python et R. De plus, envisagez notre parcours professionnel de Scientifique en Machine Learning en Python. Je vous promets, vous apprendrez beaucoup.
Source:
https://www.datacamp.com/tutorial/negative-binomial-distribution













