自組織映射：帶有 Python 範例的直觀指南

教學
Python

自組織地圖（SOM）是一種用於無監督學習任務的人工神經網絡，例如聚類。給定一組數據點，該模型學習將數據劃分為不同的聚類。SOM將複雜的多維數據投影到較低維度（通常是2維）的網格上，這使得可視化變得更加容易。因此，SOM也用於可視化高維數據。

在本教程中，我們將探討SOM的核心概念、其學習過程及其典型使用案例。我們將解釋如何使用MiniSom庫在Python中實現SOM，以及如何直觀地表示結果。最後，我們討論訓練SOM模型中的重要超參數及如何對其進行微調。

了解自組織地圖（SOM）

在本節中，我們介紹自組織地圖（SOM）的核心概念、其學習過程和應用案例。

自組織地圖的核心概念

自組織地圖涉及一組重要的概念，了解這些概念是必要的。

神經元

自組織地圖本質上是一個神經元的網格。在訓練過程中，與輸入數據點的權重向量最接近的神經元會調整其權重以及鄰近神經元的權重，以便與輸入數據點更緊密地匹配。經過多次迭代，鄰近神經元的組會映射到相關的數據點，這導致了輸入數據集的聚類。

網格結構

自組織映射（SOM）中的神經元以網格形式組織。相鄰的神經元對應於相似的數據點。較大的數據集需要較大的網格。通常，這個網格是二維的。網格結構作為低維空間，用於將高維數據映射到此空間。該網格有助於可視化數據模式和集群。

映射數據點

每個數據點都會使用距離度量與所有神經元進行比較。權重向量與輸入數據點最接近的神經元是該數據點的最佳匹配單元（BMU）。

一旦識別出最佳匹配單元（BMU），BMU及其鄰近神經元的權重會被更新。這次更新使得BMU和鄰近神經元更接近輸入數據點。這種映射保持了數據的拓撲結構，確保相似的數據點被映射到相鄰的神經元。

自組織映射（SOM）的學習過程

自組織映射的訓練被視為無監督，因為它不依賴於標記數據集。訓練自組織映射的目標是迭代調整神經元的權重向量，以便相似的數據點被映射到相鄰的神經元。

競爭學習

SOM 使用競爭學習（而非梯度下降和反向傳播）。神經元之間競爭成為每個輸入數據點的最佳匹配單元（BMU）。距離數據點最近的神經元被確定為其 BMU。BMU 及其相鄰的神經元會被更新，以進一步減少它們與數據點之間的距離。相鄰的神經元映射到相關的數據點。這導致神經元之間的專業化及輸入數據點的聚類。

距離函數

SOM 使用距離函數來測量神經元與數據點之間的距離。這個距離用來確定每個數據點的 BMU。MiniSom 提供四種距離函數可供選擇：

鄰域函數

在識別出資料點的最佳匹配單位（BMU）後，BMU及其相鄰神經元會朝向該資料點的方向進行更新。鄰域函數確保自組織映射（SOM）保持輸入資料的拓撲關係。鄰域函數決定：

  • 哪些神經元被視為BMU的鄰域
  • 相鄰神經元更新的程度。一般來說，離BMU更近的神經元會比離得更遠的神經元獲得更大的調整

MiniSom 提供三種鄰域函數：

  • 高斯（這是預設值）。
  • 氣泡
  • 墨西哥帽
  • 三角形

迭代過程

SOM 的學習過程在多個迭代中進行。在每次迭代中，SOM 處理許多輸入數據點。我們將學習過程概述如下步驟：

  • 當訓練開始時，所有神經元的權重都是（隨機）初始化的。
  • 給定一個輸入數據點，每個神經元計算其與輸入的距離。
    • 距離最小的神經元被稱為最佳匹配單元（BMU）。
  • BMU及其鄰近神經元的權重會被調整，以更接近輸入向量。這種調整的程度由以下因素決定：
    • 鄰域函數：距離BMU較遠的神經元更新的程度低於距離BMU較近的神經元。這樣可以保留數據的拓撲結構。
    • 學習率：較高的學習率會導致較大的更新。

這些步驟在多次迭代中重複進行，遍歷許多輸入數據點。權重會逐漸更新，以便映射自我組織並捕捉數據的結構。

學習率和鄰域半徑通常隨著時間的推移而減少，允許SOM逐漸微調權重。在本教程的後面，我們將使用Python代碼實現迭代訓練過程的步驟。

典型的SOM使用案例

由於其獨特的架構，SOM在機器學習、分析和可視化方面有幾個典型應用。

聚類

SOMs 用於將高維數據分組為相似數據點的聚類。這有助於識別數據中的內在結構。每個神經元映射到密切相關的數據點，相似的數據點被映射到相同或相鄰的神經元，從而形成明顯的聚類。

例如，在行銷中，SOMs 可以根據購買行為將客戶分組。這將使品牌能夠為不同的客戶細分（聚類）量身定制行銷策略。

降維

SOMs 可以將具有多個特徵向量的高維數據映射到一個維度較少的網格（通常為二維網格）。由於這種映射保持了數據點之間的關係，降低的維度使得可視化複雜數據集變得更加容易，而不會顯著損失信息。

除了讓可視化和分析任務變得更容易外，自組織映射（SOM）還可以在應用其他機器學習算法之前減少數據的維度。SOM也用於圖像處理，通過對具有相似特徵的像素或區域進行聚類，來減少特徵的數量，使得圖像識別和分類任務更加高效。

異常檢測

在訓練過程中，大多數數據點會被映射到特定的神經元。異常（不適合任何聚類的數據點）通常會被映射到遠離或人數較少的神經元。這些離群值不適合學習到的聚類，並被映射到距離正常數據點的最佳匹配單元（BMU）較遠的神經元。

例如，將金融交易映射到SOM網格上，可以幫助我們識別出不尋常的活動（離群值），這可能表示潛在的欺詐行為。

數據可視化

資料視覺化是自組織映射（SOM）的最常見應用案例之一。高維度資料難以視覺化。SOM 通過降低資料的維度並將其投影到二維網格上，使視覺化變得更加容易。這也有助於檢測資料中的聚類和異常的資料點，這在原始資料中會比較複雜。 

例如，資料視覺化使分析高維人口資料變得更簡單。在二維網格上繪製資料將有助於發現不同人口群體之間的相似性和差異。  

在討論 SOM 的核心概念和應用案例之後，我們將展示如何使用 Python 套件 MiniSom 來實現它們，在接下來的幾個部分中。 

您可以在 這個 DataLab 筆記本 上訪問和運行完整的程式碼。

為 SOM 設置環境

在建立SOM之前，我們需要準備必要的套件環境。

安裝Python函式庫

我們需要這些套件：

  • MiniSom是一個基於NumPy的Python工具，用於創建和訓練SOM。
  • NumPy用於訪問數學函數，例如拆分數組、獲取唯一值等。
  • matplotlib用於繪製各種圖形和圖表，以可視化數據。
  • 來自sklearn的datasets包用於導入可應用於SOM的數據集。
  • 來自sklearn的MinMaxScaler包用於對數據集進行標準化。

以下代碼片段導入這些包：

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

準備數據集

在這個教學中，我們使用 MiniSom 來建立一個 SOM，然後在 標準 IRIS 數據集 上進行訓練。這個數據集包含三類鳶尾花。每類有 50 個實例。為了準備數據，我們遵循以下步驟：

  • 從 sklearn 導入 Iris 數據集，
  • 提取數據向量和目標標量。
  • 標準化數據向量。在本教程中，我們使用 scikit-learn 的 MinMaxScaler。
  • 為三種鸢尾花類別聲明一組標籤。

以下代碼實現這些步驟：

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

在 Python 中實現自組織映射 (SOM)

要在 Python 中實現 SOM，我們首先定義並初始化網格，然後在數據集上進行訓練。接著，我們可以可視化訓練後的神經元和聚類數據集。

定義 SOM 網格

如前所述，自組織映射（SOM）是一個神經元網格。使用MiniSom，我們可以創建二維網格。網格的X和Y維度是沿每個軸的神經元數量。要定義SOM網格，我們還需要指定：

  • 網格的X和Y維度
  • 輸入變量的數量 – 這是數據行的數量。

將這些參數聲明為Python常量：

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

以下示例代碼說明了如何使用MiniSom聲明網格：

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

前兩個參數是沿X和Y軸的神經元數量，第三個參數是變量的數量。

我們在創建SOM網格時聲明其他參數和超參數。我們將在教程中稍後解釋這些。現在，請根據以下顯示聲明這些參數：

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

使用這些參數創建SOM：

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

初始化神經元

上述命令為所有神經元創建了一個具有隨機權重的SOM。使用從數據中抽取的權重來初始化神經元（而不是隨機數字）可以使訓練過程更加高效。

使用MiniSom創建自組織映射（SOM）時，有兩種方法可以根據數據初始化神經元的權重：

  • 隨機初始化：神經元的初始權重是從輸入數據中隨機抽取的。我們通過對自組織映射（SOM）應用.random_weights_init()函數來實現這一點。
  • PCA初始化：主成分分析（PCA）初始化使用輸入數據的主成分來初始化權重。神經元的初始權重跨越前兩個主成分。這通常會導致更快的收斂。

在本指南中，我們使用PCA初始化。要在SOM權重上應用PCA初始化，請使用.pca_weights_init()函數，如下所示：

som.pca_weights_init(data)

訓練SOM

訓練過程更新SOM權重，以最小化神經元與數據點之間的距離。

以下是我們解釋的迭代訓練過程：

  • 初始化：所有神經元的權重向量被初始化，通常使用隨機值。也可以通過對輸入數據分佈進行抽樣來初始化權重。
  • 輸入選擇: 從訓練數據集中（隨機）選擇一個輸入向量。
  • BMU識別: 與輸入向量權重向量最接近的神經元被識別為BMU。
  • 鄰域更新：BMU及其相鄰神經元更新它們的權重向量。學習率和鄰域函數決定了哪些神經元被更新以及更新的幅度。在迭代步驟t，給定輸入向量x，神經元i的權重向量為wi，學習率(t)，以及鄰域函數hbi（此函數量化了給定BMU神經元b的神經元i的更新幅度），神經元i的權重更新公式表達為：
  • 學習率與鄰域半徑的衰減率：學習率和鄰域半徑隨著時間的推移而減少。在早期的迭代中，訓練過程對較大鄰域進行較大的調整。後期的迭代則通過對相鄰神經元的權重進行較小的更改來幫助微調權重。這使得地圖能夠穩定並收斂。

為了訓練SOM，我們將輸入數據提供給模型。我們可以從兩種方法中選擇其一來進行此操作：

  • 從輸入數據中隨機選取樣本。.train_random()函數實現了這種技術。
  • 依序處理輸入數據中的向量。這是通過 .train_batch() 函數來完成的。

這些函數接受輸入數據和迭代次數作為參數。在本指南中，我們使用 .train_random() 函數。將迭代次數聲明為常量並傳遞給訓練函數：

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)

執行腳本並完成訓練後，會顯示一條包含量化誤差的消息：

quantization error: 0.05357240680504421

量化誤差指示了在自組織映射（SOM）對數據進行量化（降低維度）時所損失的信息量。較大的量化誤差表示神經元與數據點之間的距離較大。這也意味著聚類的可靠性較低。

可視化SOM神經元

我們現在擁有一個訓練好的SOM模型。為了可視化它，我們使用距離圖（也稱為 U-矩陣）。距離圖顯示SOM的神經元作為一個單元格網格。每個單元格的顏色代表其與鄰近神經元的距離。

距離圖是一個與SOM具有相同維度的網格。距離圖中的每個單元格是神經元與其鄰居之間（歐幾里得）距離的標準化總和。

訪問 SOM 距離圖 使用 .distance_map() 函數。生成 U 矩陣的步驟如下：

  • 使用 pyplot 創建一個與 SOM 相同尺寸的圖形。在此例中，尺寸為 8×8。
  • 使用 matplotlib 繪製距離圖，使用 .pcolor() 函數。在此例中，我們使用 gist_yarg 作為配色方案。
  • 顯示 colorbar，一個將不同顏色映射到不同標量值的索引。在這種情況下，由於距離已被標準化，標量距離值範圍從 0 到 1。

以下代碼實現了這些步驟：

# 創建網格
plt.figure(figsize=(8, 8))
# 繪製距離圖
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# 顯示顏色條
plt.colorbar()
plt.show()

在這個例子中，U-矩陣使用了單調顏色方案。可以根據以下指導原則來理解：

  • 較淺的色調代表緊密排列的神經元，而較深的色調則代表與其他神經元距離較遠的神經元。
  • 較淺色調的群組可以被解釋為集群。集群之間的深色節點可以被解釋為集群之間的邊界。

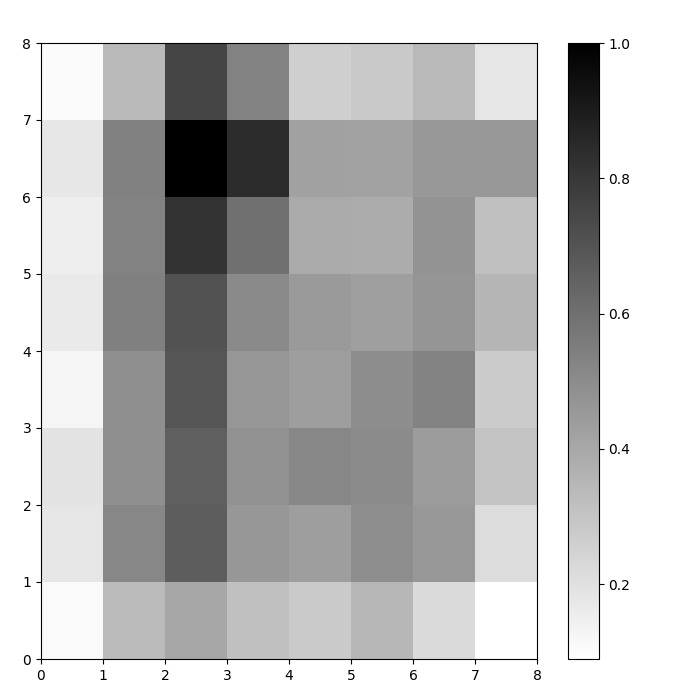
圖 1：基於虹膜數據集訓練的SOM的U矩陣（圖片由作者提供）

評估SOM聚類結果

前面的圖形直觀地展示了SOM的神經元。在這一部分，我們將展示如何視覺化SOM如何對數據進行聚類。

識別集群

我們在上述U矩陣上疊加標記，以表示每個單元（神經元）所代表的虹膜植物類別。為此：

  • 如前所述，使用pyplot創建一個8×8的圖形，繪製距離圖，並顯示顏色條。
  • 指定一個包含三個matplotlib標記的數組，每個類別對應一個Iris植物。
  • 指定一個包含三個matplotlib顏色代碼的數組，每個類別對應一個Iris植物。
  • 逐步繪製每個數據點的獲勝神經元：
    • 使用 .winner() 函數確定每個數據點的勝利神經元（坐標）。
    • 在網格中每個單元格的中間繪製每個勝利神經元的位置。w[0] 和 w[1] 分別給出神經元的 X 和 Y 坐標。為了將其繪製在單元格的中間，對每個坐標加上 0.5。

以下代碼顯示了如何做到這一點：

# 繪製距離圖
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# 為每個類別創建標記和顏色
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# 繪製每個數據點的勝利神經元
for count, datapoint in enumerate(data):
    # 獲取勝利者
    w = som.winner(datapoint)  
    # 在樣本數據點的獲勝位置放置標記
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

結果圖像如下所示：

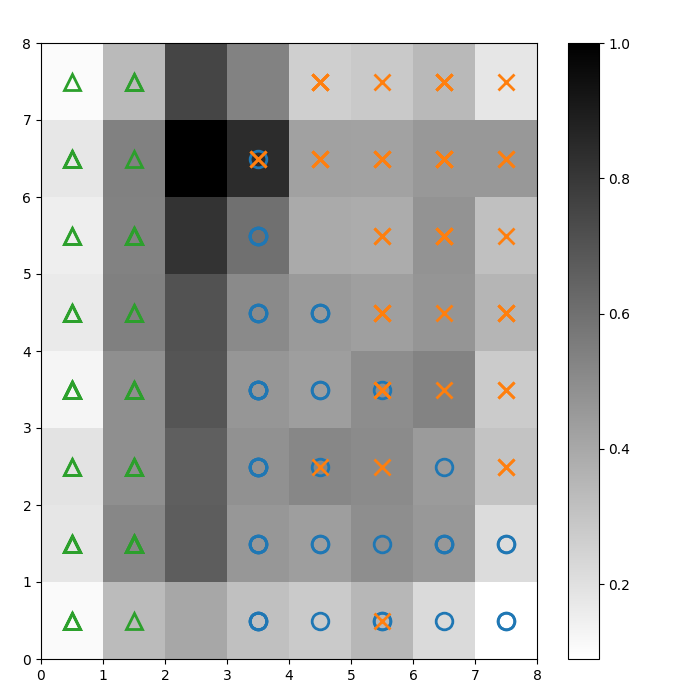
圖 2：帶有類別標記的 U 矩陣（圖像來源：作者）

根據 Iris 數據集文檔，“一個類別可以與其他兩個類別線性可分；後者之間則無法線性可分。” 在上面的 U 矩陣中，這三個類別分別用三個標記表示 – 三角形、圓形和十字形。

請注意，藍色圓形和橙色十字形之間並沒有明確的邊界。此外，兩個類別在許多神經元上重疊在同一個神經元上。這意味著該神經元與兩個類別的距離相等。

可視化聚類結果

自組織映射（SOM）是一種聚類模型。相似的數據點映射到同一個神經元。相同類別的數據點映射到一群相鄰的神經元。我們將所有數據點繪製在SOM網格上，以便更好地研究聚類行為。

以下步驟描述如何創建此散點圖：

  • 獲取每個數據點的獲勝神經元的X和Y坐標。
  • 繪製距離圖，就像我們在圖1中所做的那樣。
  • 使用 plt.scatter() 來繪製每個數據點的所有獲勝神經元的散點圖。為每個點添加隨機偏移，以避免同一個細胞內數據點之間的重疊。

我們在下面的代碼中實現這些步驟：

# 獲取每個數據點的獲勝神經元的 X 和 Y 坐標w_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# 繪製距離圖
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# 繪製每個數據點的所有獲勝神經元的散點圖
# 為每個點添加隨機偏移以避免重疊
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

以下圖表顯示了輸出的散點圖：

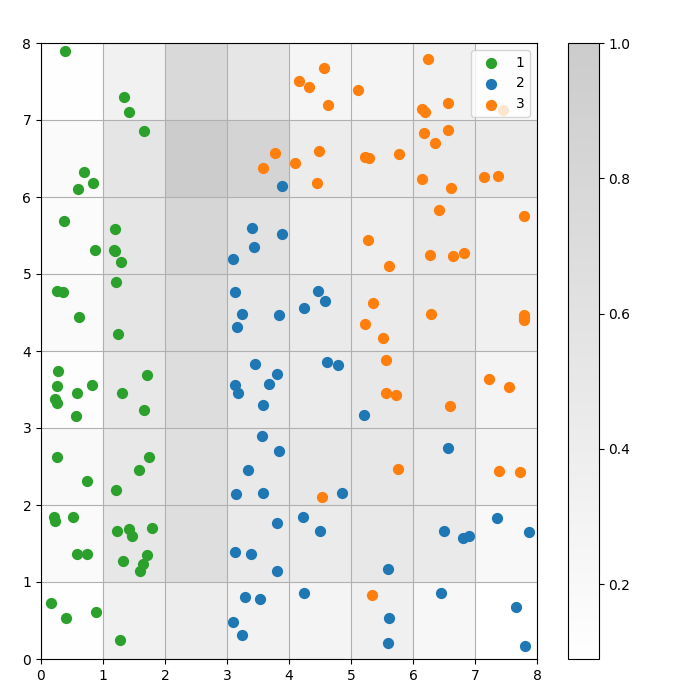圖 3：細胞內數據點的散佈圖（圖片由作者提供）

在上述散佈圖中，觀察到：

  • 一些細胞包含藍色和橙色的點。
  • 綠色的點與其餘數據明顯分開，但藍色和橙色的點並未乾淨地分開。
  • 上述觀察與Iris數據集中只有三個聚類中的一個具有明確邊界的事實相符。
  • 在圖1中，聚類之間的深色節點（可以解釋為聚類之間的邊界）與散點圖中的空白單元格相匹配。

您可以在這個DataLab筆記本上訪問並運行完整的代碼。

調整SOM模型

前面的部分展示了如何創建和訓練SOM模型，以及如何以視覺方式研究結果。在本節中，我們討論如何調整SOM模型的性能。

關鍵超參數調整

與任何機器學習模型一樣，超參數對模型的性能有著顯著影響。

在訓練自組織映射（SOM）中，一些重要的超參數包括：

  • 該網格大小決定了地圖的大小。具有AxB網格大小的地圖中的神經元數量為A*B。
  • 學習率決定每次迭代中權重的調整幅度。我們設定初始學習率，並根據衰減函數隨時間遞減。
  • 衰減函數決定每次後續迭代中學習率減少的程度。
  • 該鄰域函數是一種數學函數，指定哪些神經元被視為最佳匹配單元（BMU）的鄰居。
  • 該標準差指定鄰域函數的擴展範圍。例如，一個具有高標準差的高斯鄰域函數將擁有比同一函數具有較小標準差的更大鄰域。我們設定初始標準差，隨著時間的推移，根據Sigma衰減函數而減少。
  • 該 sigma 衰減 函數控制每次後續迭代中標準差減少的程度。
  • 該 訓練迭代次數 決定了權重更新的次數。在每次訓練迭代中，神經元的權重會更新一次。
  • 距離函數是一個數學函數，用於計算神經元與數據點之間的距離。
  • 拓撲決定了網格結構的布局。網格中的神經元可以排列成矩形或六邊形模式。

在下一節中，我們將討論設置這些超參數值的指導原則。

超參數調整的影響

超參數的值應根據模型和數據集來決定。在某種程度上，確定這些值是一個反覆試驗的過程。在本節中，我們提供每個超參數調整的指導。在每個超參數旁邊，我們提到（在括號中）示例代碼中使用的相應 Python 常量。

  • 網格大小 (SOM_X_AXIS_NODES 和 SOM_X_AXIS_NODES): 網格大小取決於數據集的大小。基本規則是，給定一個大小為 N 的數據集，網格應該大約包含 5*sqrt(N) 個神經元。例如，如果數據集有 150 個樣本，則網格應該包含 5*sqrt(150) = 大約 61 個神經元。在本教程中，Iris 數據集有 150 行，我們使用 8×8 的網格。 
  • 初始學習率(ALPHA): 較高的學習率可以加快收斂速度，而較低的學習率則用於在早期迭代後進行更細微的調整。初始學習率應足夠大以便快速適應，但又不能過大以致於超過最佳權重值。在本文中，初始學習率為0.5。
  • 初始標準差(SIGMA0): 它決定了鄰域的初始大小或範圍。較大的值考慮更多的全局模式。在這個例子中，我們使用的起始標準差為1.5。
  • 對於 衰減率 (DECAY_FUNC) 和 西格瑪衰減率 (SIGMA_DECAY_FUNC)，我們可以從三種衰減函數中選擇一種： 
    • 反向衰減: 如果數據同時具有全局和局部模式，這個函數是合適的。在這種情況下，我們需要較長的廣泛學習階段，然後再專注於局部模式。
    • 線性衰減: 這適用於我們希望保持穩定和均勻的鄰域大小或學習率降低的數據集。如果數據不需要太多微調，這是很有用的。
    • 漸近衰減: 如果數據複雜且維度高，這個函數是有用的。在這種情況下，最好花更多時間進行全局探索，然後再逐漸過渡到更細的細節。
  • 鄰域函數 (NEIGHBORHOOD_FUNC): 鄰域函數的預設選擇是高斯函數。其他函數，如下所述，也會被使用。
    • 高斯（預設）：這是一個鐘形曲線。隨著神經元與獲勝神經元的距離增加，神經元更新的程度會平滑地減少。它提供了一個平滑且連續的過渡，並保留數據的拓撲結構。由於其穩定且可預測的行為，適用於大多數一般用途。
    • 泡沫: 此功能創建一個固定寬度的鄰域。該鄰域內的所有神經元都會同等更新，而該鄰域外的神經元則不會更新（對於給定的數據點）。這在計算上更便宜且更易於實現。它對於較小的地圖非常有用，在這些地圖中，明確的鄰域邊界不會妨礙有效的聚類。
    • 墨西哥帽: 它有一個中央的正區域，周圍是負區域。接近最佳匹配單元（BMU）的神經元會被更新以接近數據點，而遠離的神經元則被更新以遠離數據點。這種技術增強了對比度並提升了地圖中的特徵。由於它強調明顯的聚類，因此在需要清晰區分聚類的模式識別任務中非常有效。
    • 三角形：此功能將鄰域大小定義為三角形，BMU具有最大的影響力。它隨著與BMU的距離線性減少。這適用於數據的聚類，特別是那些在聚類或特徵之間具有漸進過渡的數據，如圖像、語音或時間序列數據，其中相鄰數據點預期共享相似特徵。
  • 距離函數（DISTANCE_FUNC）：為了測量神經元和數據點之間的距離，我們可以選擇四種方法：
    • 歐幾里得距離（預設選擇）：當資料是連續的，並且我們想要測量直線距離時非常有用。它適合大多數一般任務，特別是當數據點均勻分佈且在空間上相關時。
    • 餘弦距離：對於文本或高維稀疏數據來說是一個不錯的選擇，因為向量之間的角度比大小更為重要。它對於比較數據的方向性非常有用。
    • 曼哈頓距離：當數據點位於網格或格子上（例如，城市街區）時理想。這對於異常值的敏感度低於歐幾里得距離。
    • 切比雪夫距離: 適用於可以朝任何方向移動的情況（例如：棋盤距離）。它對於離散空間特別有用，因為我們希望優先考慮最大軸差。
  • 拓撲 (TOPOLOGY): 在一個網格中，神經元可以排列成六角形或矩形結構：
    • 矩形（默認）：每個神經元有4個直接鄰居。當數據沒有明確的空間關係時，這是合適的選擇。它在計算上也更簡單。
    • 六邊形：每個神經元有6個鄰居。如果數據的空間關係更適合用六邊形網格表示，這是首選選項。這種情況出現在圓形或角度數據分佈中。
  • 訓練迭代次數 (N_ITERATIONS): 原則上，較長的訓練時間會導致較低的錯誤率，並使權重更好地與輸入數據對齊。然而，模型的性能隨著迭代次數的增加而漸近增長。因此，在達到一定的迭代次數後，隨後迭代所帶來的性能提升僅為微不足道。確定正確的迭代次數需要一些實驗。在本教程中，我們對模型進行了5000次迭代的訓練。

為了確定超參數的正確配置，我們建議在數據的較小子集上嘗試不同的選項。

結論

自組織映射是一種穩健的 無監督學習 工具。它們用於聚類、降維、異常檢測和數據可視化。由於它們保留了高維數據的拓撲特性並將其表示在低維網格上，SOM使得可視化和解釋複雜數據集變得容易。

本教程討論了SOM的基本原理，並展示了如何使用MiniSom Python庫實現SOM。它還演示了如何進行結果的視覺分析，並解釋了用於訓練SOM和微調其性能的重要超參數。

Source:
https://www.datacamp.com/tutorial/self-organizing-maps