Selbstorganisierende Karten: Ein intuitiver Leitfaden mit Python-Beispielen

Einrichten der Umgebung für SOM

Bevor wir das SOM erstellen, müssen wir die Umgebung mit den erforderlichen Paketen vorbereiten.

Python-Bibliotheken installieren

Wir benötigen diese Pakete:

• MiniSom ist ein auf NumPy basierendes Python-Tool, das SOMs erstellt und trainiert.
• NumPy wird verwendet, um auf mathematische Funktionen wie das Teilen von Arrays, das Abrufen einzigartiger Werte usw. zuzugreifen.
• matplotlib wird verwendet, um verschiedene Grafiken und Diagramme zur Visualisierung der Daten zu erstellen.
• Das datasets Paket von sklearn wird verwendet, um Datensätze zu importieren, auf die das SOM angewendet werden soll. 
• Das MinMaxScaler Paket von sklearn normalisiert den Datensatz. 

Der folgende Codeausschnitt importiert diese Pakete: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Den Datensatz vorbereiten

In diesem Tutorial verwenden wir MiniSom, um ein SOM zu erstellen und es dann mit dem kanonischen IRIS-Datensatz zu trainieren. Dieser Datensatz besteht aus 3 Klassen von Iris-Pflanzen. Jede Klasse hat 50 Instanzen. Um die Daten vorzubereiten, folgen wir diesen Schritten: 

• Importieren Sie den Iris-Datensatz von sklearn, 
• Extrahieren Sie die Datenvektoren und die Zielskalare. 
• Normalisieren Sie die Datenvektoren. In diesem Tutorial verwenden wir den MinMaxScaler von scikit-learn. 
• Erklären Sie eine Menge von Labels für jede der drei Klassen von Iris-Pflanzen.

Der folgende Code implementiert diese Schritte:

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Implementierung von Selbstorganisierenden Karten (SOM) in Python

Um ein SOM in Python zu implementieren, definieren und initialisieren wir das Gitter, bevor wir es mit dem Datensatz trainieren. Wir können dann die trainierten Neuronen und den gruppierten Datensatz visualisieren.

Definition des SOM-Gitters

Wie bereits erwähnt, ist ein SOM ein Gitter von Neuronen. Mit MiniSom können wir 2-dimensionale Gitter erstellen. Die X- und Y-Dimensionen des Gitters sind die Anzahl der Neuronen entlang jeder Achse. Um das SOM-Gitter zu definieren, müssen wir auch Folgendes angeben:

• Die X- und Y-Dimensionen des Gitters
• Die Anzahl der Eingangsvariablen – dies ist die Anzahl der Datenzeilen.

Erklären Sie diese Parameter als Python-Konstanten:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

Der folgende Beispielcode zeigt, wie man das Gitter mit MiniSom deklariert:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

Die ersten beiden Parameter sind die Anzahl der Neuronen entlang der X- und Y-Achsen, und der dritte Parameter ist die Anzahl der Variablen.

Wir deklarieren andere Parameter und Hyperparameter, während wir das SOM-Gitter erstellen. Wir werden diese später im Tutorial erklären. Für den Moment deklarieren Sie diese Parameter wie unten gezeigt:

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Erstellen Sie ein SOM mit diesen Parametern:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Initialisierung der Neuronen

Der obige Befehl erstellt ein SOM mit zufälligen Gewichten für alle Neuronen. Die Neuronen mit Gewichten zu initialisieren, die aus den Daten entnommen werden (anstatt mit Zufallszahlen), kann den Trainingsprozess effizienter gestalten.

Bei der Verwendung von MiniSom zur Erstellung einer Selbstorganisierenden Karte (SOM) gibt es zwei Möglichkeiten, die Gewichte der Neuronen basierend auf den Daten zu initialisieren:

• Zufällige Initialisierung: Die ursprünglichen Gewichte der Neuronen werden zufällig aus den Eingabedaten gezogen. Dies erreichen wir, indem wir die .random_weights_init() Funktion auf das SOM anwenden.
• PCA-Initialisierung: Die Hauptkomponentenanalyse (PCA) verwendet die Hauptkomponenten der Eingabedaten zur Initialisierung der Gewichte. Die ursprünglichen Gewichte der Neuronen decken die ersten beiden Hauptkomponenten ab. Dies führt oft zu einer schnelleren Konvergenz.

In diesem Leitfaden verwenden wir die PCA-Initialisierung. Um die PCA-Initialisierung auf die SOM-Gewichte anzuwenden, verwenden Sie die .pca_weights_init() Funktion, wie unten gezeigt:

som.pca_weights_init(data)

Training des SOM

Der Trainingsprozess aktualisiert die SOM-Gewichte, um die Distanz zwischen den Neuronen und den Datenpunkten zu minimieren.

Im Folgenden erklären wir den iterativen Trainingsprozess:

• Initialisierung: Die Gewichtungsvektoren aller Neuronen werden initialisiert, typischerweise mit zufälligen Werten. Es ist auch möglich, die Gewichte durch Abtasten der Eingabedatenverteilung zu initialisieren.
• Auswahl der Eingabe: Ein Eingabevektor wird (zufällig) aus dem Trainingsdatensatz ausgewählt.
• BMU-Identifikation: Das Neuron mit dem Gewichtvektor, der dem Eingabevektor am nächsten ist, wird als BMU identifiziert.
• Nachbarschaftsaktualisierung: Der BMU und seine benachbarten Neuronen aktualisieren ihre Gewichtungsvektoren. Die Lernrate und die Nachbarschaftsfunktion entscheiden, welche Neuronen aktualisiert werden und in welchem Maße. Im Iterationsschritt t, gegebenen dem Eingangsvektor x, der Gewichtungsvektor des Neurons i als w_i, die Lernrate (t), und die Nachbarschaftsfunktion h_bi (diese Funktion quantifiziert das Ausmaß der Aktualisierung für das Neuron i gegeben dem BMU-Neuron b), wird die Gewichtungsaktualisierungsformel für das Neuron i wie folgt ausgedrückt:
• Abnahme der Lernrate und des Nachbarschaftsradius: Sowohl die Lernrate als auch der Nachbarschaftsradius nehmen im Laufe der Zeit ab. In den früheren Iterationen nimmt der Trainingsprozess größere Anpassungen über einen größeren Nachbarschaftsbereich vor. Spätere Iterationen helfen, die Gewichte durch kleinere Änderungen der Gewichte benachbarter Neuronen fein abzustimmen. Dies ermöglicht es der Karte, sich zu stabilisieren und zu konvergieren.

Um das SOM zu trainieren, präsentieren wir dem Modell die Eingabedaten. Wir können aus einem von zwei Ansätzen wählen, um dies zu tun:

• Proben zufällig aus den Eingabedaten auswählen. Die .train_random() Funktion implementiert diese Technik.
• Durchlaufe nacheinander die Vektoren in den Eingabedaten. Dies geschieht mit der .train_batch() Funktion. 

Diese Funktionen akzeptieren die Eingabedaten und die Anzahl der Iterationen als Parameter. In diesem Leitfaden verwenden wir die .train_random() Funktion. Deklariere die Anzahl der Iterationen als Konstante und übergebe sie an die Trainingsfunktion: 

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

Nach der Ausführung des Skripts und dem Abschluss des Trainings wird eine Nachricht mit dem Quantisierungsfehler angezeigt:

quantization error: 0.05357240680504421 

Der Quantisierungsfehler gibt an, wie viel Information verloren geht, wenn das SOM die Daten quantisiert (die Dimensionen reduziert). Ein großer Quantisierungsfehler weist auf eine größere Distanz zwischen den Neuronen und den Datenpunkten hin. Das bedeutet auch, dass die Clusterbildung weniger zuverlässig ist.

Visualisierung von SOM-Neuronen

Wir haben jetzt ein trainiertes SOM-Modell. Um es zu visualisieren, verwenden wir eine Distanzkarte (auch bekannt als U-Matrix). Die Distanzkarte zeigt die Neuronen des SOM als ein Gitter von Zellen an. Die Farbe jeder Zelle repräsentiert ihre Distanz zu den benachbarten Neuronen.

Die Distanzkarte ist ein Gitter mit den gleichen Abmessungen wie das SOM. Jede Zelle in der Distanzkarte ist die normierte Summe der (euklidischen) Distanzen zwischen einem Neuron und seinen Nachbarn.

Greifen Sie auf die SOM-Distanzkarte mit der Funktion .distance_map() zu. Um die U-Matrix zu generieren, folgen wir diesen Schritten:

• Verwenden Sie pyplot , um eine Abbildung mit denselben Abmessungen wie das SOM zu erstellen. In diesem Beispiel sind die Abmessungen 8×8. 
• Plottieren Sie die Distanzkarte mit matplotlib unter Verwendung der .pcolor() Funktion. In diesem Beispiel verwenden wir gist_yarg als Farbpalette.
• Zeige die colorbar, einen Index, der verschiedene Farben verschiedenen Skalaren zuordnet. In diesem Fall, da die Abstände normalisiert sind, reichen die skalaren Distanzwerte von 0 bis 1. 

Der folgende Code implementiert diese Schritte: 

# Erstelle das Gitter
plt.figure(figsize=(8, 8))
# Zeichne die Distanzkarte
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# Zeige die Farbskala
plt.colorbar()
plt.show()

In diesem Beispiel verwendet die U-Matrix ein monotones Farbschema. Sie kann anhand dieser Richtlinien verstanden werden:

• Helle Farbtöne repräsentieren eng beieinander liegende Neuronen, und dunklere Farbtöne repräsentieren Neuronen, die weiter voneinander entfernt sind. 
• Gruppen von helleren Farbtönen können als Cluster interpretiert werden. Dunkle Knoten zwischen den Clustern können als die Grenzen zwischen den Clustern interpretiert werden.

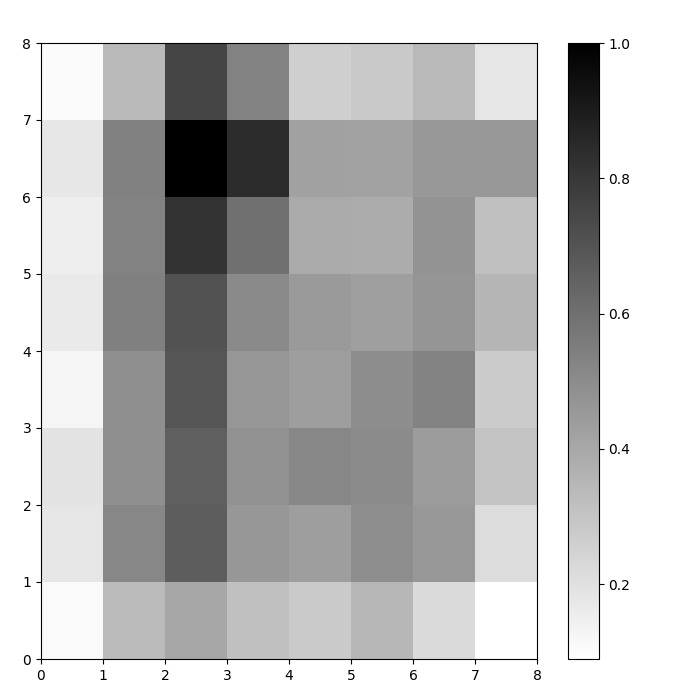
Abbildung 1: U-Matrix des SOM, trainiert mit dem Iris-Datensatz (Bild vom Autor)

Bewertung der SOM-Clustering-Ergebnisse

Die vorherige Abbildung hat grafisch die Neuronen des SOM dargestellt. In diesem Abschnitt zeigen wir, wie man visualisiert, wie das SOM die Daten gruppiert hat.

Cluster identifizieren

Wir überlagern Marker über die obenstehende U-Matrix, um anzuzeigen, zu welcher Klasse der Iris-Pflanze jede Zelle (Neuron) gehört. Um dies zu tun:

• Wie zuvor, erstellen Sie eine 8×8 Figur mit pyplot, plotten Sie die Distanzkarte und zeigen Sie die Farbskala an. 
• Geben Sie ein Array von drei matplotlib-Markern an, einen für jede Klasse der Iris-Pflanze. 
• Geben Sie ein Array von drei matplotlib-Farbcodes an, einen für jede Klasse der Iris-Pflanze. 
• Plotten Sie iterativ das gewinnende Neuron für jeden Datenpunkt:
• Bestimmen Sie die (Koordinaten des) Gewinnerneurons für jeden Datenpunkt mit der Funktion .winner(. 
• Zeichnen Sie die Position jedes Gewinnerneurons in der Mitte jeder Zelle im Raster. w[0] und w[1] geben die X- und Y-Koordinaten des Neurons an. Ein Wert von 0,5 wird zu jeder Koordinate addiert, um sie in der Mitte der Zelle zu plotten. 

Der folgende Code zeigt, wie man das macht:

# plotte die Distanzkarte
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# erstelle die Marker und Farben für jede Klasse
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# plotte das Gewinnerneuron für jeden Datenpunkt
for count, datapoint in enumerate(data):
    # hole den Gewinner
    w = som.winner(datapoint)  
    # platziere einen Marker an der Gewinnerposition für den Beispiel-Datenpunkt
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

Das resultierende Bild ist unten dargestellt:

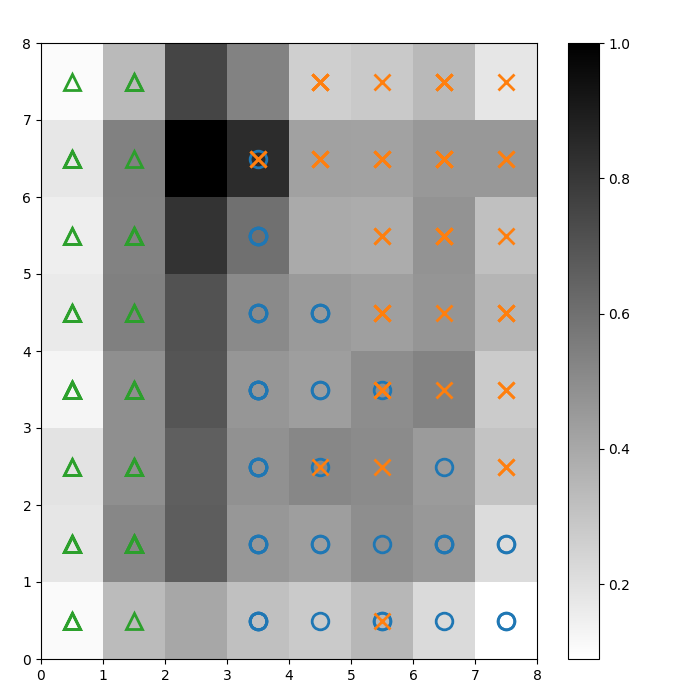
Abbildung 2: U-Matrix überlagert mit Klassenmarkierungen (Bild vom Autor)

Basierend auf der Iris-Datensatzdokumentation, „eine Klasse ist linear von den anderen 2 trennbar; letztere sind nicht linear voneinander trennbar“. In der oben gezeigten U-Matrix werden diese drei Klassen durch drei Marker dargestellt – Dreieck, Kreis und Kreuz. 

Beachten Sie, dass es keine klare Grenze zwischen den blauen Kreisen und den orangefarbenen Kreuzen gibt. Darüber hinaus sind zwei Klassen in vielen Zellen über dasselbe Neuron gelegt. Das bedeutet, dass das Neuron von beiden Klassen gleich weit entfernt ist.

Visualisierung des Clustering-Ergebnisses

Ein SOM ist ein Clustering-Modell. Ähnliche Datenpunkte werden demselben Neuron zugeordnet. Datenpunkte derselben Klasse werden einem Cluster benachbarter Neuronen zugeordnet. Wir plotten alle Datenpunkte auf dem SOM-Raster, um das Clustering-Verhalten besser zu untersuchen.

Die folgenden Schritte beschreiben, wie man dieses Streudiagramm erstellt:

• Bestimmen Sie die X- und Y-Koordinaten des gewinnenden Neurons für jeden Datenpunkt.
• Plotten Sie die Distanzkarte, wie wir es für Abbildung 1 getan haben.
• Verwenden Sie plt.scatter(), um ein Streudiagramm aller gewinnenden Neuronen für jeden Datenpunkt zu erstellen. Fügen Sie jedem Punkt eine zufällige Verschiebung hinzu, um Überlappungen zwischen Datenpunkten innerhalb derselben Zelle zu vermeiden.

Wir setzen diese Schritte im folgenden Code um:

# Holen Sie sich die X- und Y-Koordinaten des gewinnenden Neurons für jeden Datenpunktw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# Zeichnen Sie die Distanzkarte
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# Erstellen Sie ein Streudiagramm aller gewinnenden Neuronen für jeden Datenpunkt
# Fügen Sie jedem Punkt eine zufällige Verschiebung hinzu, um Überlappungen zu vermeiden
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

Das folgende Diagramm zeigt das ausgegebene Streudiagramm:

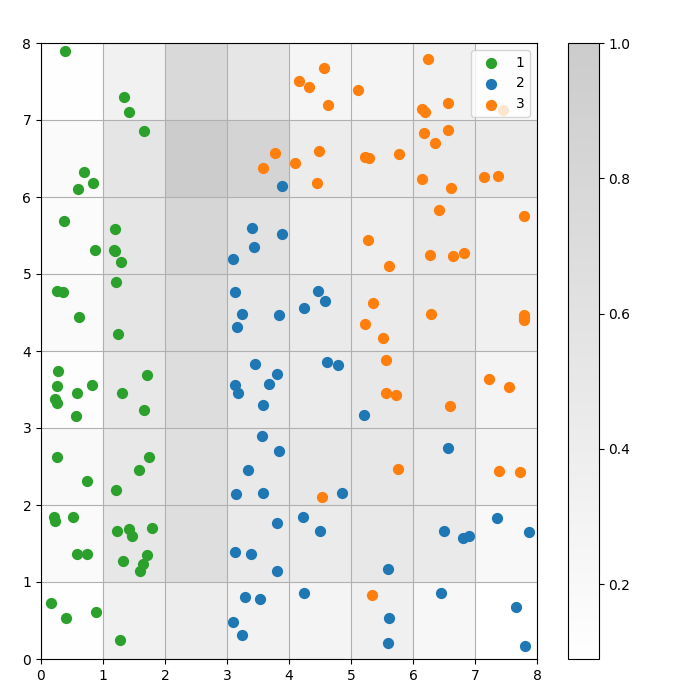Abbildung 3: Streudiagramm der Datenpunkte innerhalb der Zellen (Bild vom Autor)

Beobachten Sie im obigen Streudiagramm, dass:

• Einige Zellen sowohl blaue als auch orangefarbene Punkte enthalten.
• Die grünen Punkte sind deutlich von den restlichen Daten getrennt, während die blauen und orangefarbenen Punkte nicht klar voneinander getrennt sind.
• Die obigen Beobachtungen stimmen mit der Tatsache überein, dass nur einer der drei Cluster im Iris-Datensatz eine klare Grenze hat.
• In Abbildung 1 entsprechen dunkle Knoten zwischen den Clustern (die als die Grenzen zwischen den Clustern interpretiert werden können) leeren Zellen im Streudiagramm.

Sie können den vollständigen Code in diesem DataLab-Notizbuch aufrufen und ausführen.

Einstellung des SOM-Modells

Die vorhergehenden Abschnitte zeigten, wie man ein SOM-Modell erstellt und trainiert und wie man die Ergebnisse visuell untersucht. In diesem Abschnitt diskutieren wir, wie man die Leistung von SOM-Modellen optimiert.

Wichtige Hyperparameter zur Anpassung

Wie bei jedem maschinellen Lernmodell haben Hyperparameter einen erheblichen Einfluss auf die Leistung des Modells.

Einige der Hyperparameter, die beim Training von SOMs wichtig sind, sind:

• Die Rastergröße bestimmt die Größe der Karte. Die Anzahl der Neuronen in einer Karte mit einer Rastergröße von AxB beträgt A*B.
• Die Lernrate bestimmt, wie stark die Gewichte in jeder Iteration geändert werden. Wir setzen die initiale Lernrate, und sie verringert sich im Laufe der Zeit gemäß der Abklingfunktion. 
• Die Abklingfunktion bestimmt, in welchem Maße die Lernrate in jeder nachfolgenden Iteration verringert wird. 
• DieNachbarschaftsfunktion ist eine mathematische Funktion, die angibt, welche Neuronen als Nachbarn des BMU betrachtet werden sollen.
• Die Standardabweichung legt die Streuung der Nachbarschaftsfunktion fest. Zum Beispiel wird eine gaußsche Nachbarschaftsfunktion mit hoher Standardabweichung eine größere Nachbarschaft haben als dieselbe Funktion mit einer kleineren Standardabweichung. Wir setzen die anfängliche Standardabweichung, die im Laufe der Zeit gemäß der Sigma-Abklingfunktion abnimmt.
• Die Sigma-Dekay-Funktion steuert, wie stark die Standardabweichung in jeder nachfolgenden Iteration reduziert wird.
• Die Anzahl der Trainingsiterationen bestimmt, wie oft die Gewichte aktualisiert werden. In jeder Trainingsiteration werden die Neuronen-Gewichte einmal aktualisiert.
• Die Distanzfunktion ist eine mathematische Funktion, die die Distanz zwischen Neuronen und Datenpunkten berechnet.
• Die Topologie bestimmt das Layout der Gitterstruktur. Die Neuronen im Gitter können in einem rechteckigen oder hexagonalen Muster angeordnet werden.

Im nächsten Abschnitt besprechen wir Richtlinien zur Festlegung der Werte dieser Hyperparameter.

Auswirkungen der Hyperparameter-Tuning

Hyperparameterwerte sollten basierend auf dem Modell und dem Datensatz festgelegt werden. Bis zu einem gewissen Grad ist die Bestimmung dieser Werte ein Prozess des Ausprobierens. In diesem Abschnitt geben wir Richtlinien zur Anpassung jedes Hyperparameters. Neben jedem Hyperparameter erwähnen wir (in Klammern) die jeweiligen Python-Konstanten, die im Beispielcode verwendet werden.

• Rastergröße (SOM_X_AXIS_NODES und SOM_X_AXIS_NODES): Die Rastergröße hängt von der Größe des Datensatzes ab. Die Faustregel besagt, dass bei einem Datensatz der Größe N das Raster ungefähr 5*sqrt(N) Neuronen enthalten sollte. Zum Beispiel, wenn der Datensatz 150 Proben hat, sollte das Raster 5*sqrt(150) = ungefähr 61 Neuronen enthalten. In diesem Tutorial hat der Iris-Datensatz 150 Zeilen und wir verwenden ein 8×8-Raster. 
• Anfängliche Lernrate (ALPHA): Eine höhere Rate beschleunigt die Konvergenz, während niedrigere Raten für feinere Anpassungen nach den ersten Iterationen verwendet werden. Die anfängliche Lernrate sollte groß genug sein, um eine schnelle Anpassung zu ermöglichen, aber nicht so groß, dass sie die optimalen Gewichtswerte überschreitet. In diesem Artikel beträgt die anfängliche Lernrate 0,5. 
• Anfängliche Standardabweichung (SIGMA0): Sie bestimmt die anfängliche Größe oder Verbreitung der Nachbarschaft. Ein größerer Wert berücksichtigt mehr globale Muster. In diesem Beispiel verwenden wir eine Startstandardabweichung von 1,5. 
• Für die Abklingrate (DECAY_FUNC) und die Sigma-Abklingrate (SIGMA_DECAY_FUNC), können wir aus einer von drei Arten von Abklingfunktionen wählen: 
• Inverse Zerfall: Diese Funktion ist geeignet, wenn die Daten sowohl globale als auch lokale Muster aufweisen. In solchen Fällen benötigen wir eine längere Phase des breiten Lernens, bevor wir uns auf lokale Muster konzentrieren. 
• Lineares Zerfall: Dies ist gut für Datensätze, bei denen wir eine stetige und gleichmäßige Nachbarschaftsgröße oder eine Reduzierung der Lernrate wünschen. Dies ist nützlich, wenn die Daten nicht viel Feinabstimmung benötigen.
• Asymptotisches Zerfall: Diese Funktion ist nützlich, wenn die Daten komplex und hochdimensional sind. In solchen Fällen ist es besser, mehr Zeit für die globale Erkundung aufzuwenden, bevor man allmählich zu feineren Details übergeht. 
• Nachbarschaftsfunktion (NEIGHBORHOOD_FUNC): Die Standardwahl der Nachbarschaftsfunktion ist die Gaußsche Funktion. Auch andere Funktionen, wie im Folgenden erklärt, werden verwendet. 
• Gaußsche (Standard): Dies ist eine glockenförmige Kurve. Das Ausmaß, in dem ein Neuron aktualisiert wird, nimmt allmählich ab, je größer der Abstand zum gewinnenden Neuron ist. Sie bietet einen sanften und kontinuierlichen Übergang und bewahrt die Topologie der Daten. Sie ist aufgrund ihres stabilen und vorhersehbaren Verhaltens für die meisten allgemeinen Zwecke geeignet.
• Blase: Diese Funktion erstellt eine Nachbarschaft mit fester Breite. Alle Neuronen innerhalb dieser Nachbarschaft werden gleichmäßig aktualisiert, und Neuronen außerhalb dieser Nachbarschaft werden nicht aktualisiert (für einen bestimmten Datenpunkt). Es ist rechnerisch günstiger und einfacher zu implementieren. Es ist nützlich für kleinere Karten, bei denen scharfe Nachbarschaftsgrenzen das effektive Clustering nicht beeinträchtigen.
• Mexikanischer Hut: Er hat eine zentrale positive Region, die von einer negativen Region umgeben ist. Neuronen, die nahe am BMU sind, werden aktualisiert, um näher an den Datenpunkt zu kommen, und Neuronen, die weiter entfernt sind, werden aktualisiert, um sich vom Datenpunkt zu entfernen. Diese Technik verbessert den Kontrast und schärft die Merkmale in der Karte. Da sie ausgeprägte Cluster betont, ist sie effektiv bei Aufgaben der Mustererkennung, bei denen eine klare Trennung der Cluster gewünscht ist.
• Dreieck: Diese Funktion definiert die Nachbarschaftsgröße als ein Dreieck, wobei der BMU den größten Einfluss hat. Sie verringert sich linear mit der Entfernung vom BMU. Sie wird verwendet, um Daten mit allmählichen Übergängen zwischen Clustern oder Merkmalen zu clustern, wie z.B. Bild-, Sprach- oder Zeitreihendaten, bei denen benachbarte Datenpunkte ähnliche Eigenschaften teilen. 
• Abstandsmaß (DISTANCE_FUNC): Um den Abstand zwischen Neuronen und Datenpunkten zu messen, können wir aus 4 Methoden wählen:
• Euclidische Distanz (Standardauswahl): Nützlich, wenn die Daten kontinuierlich sind und wir die gerade Distanz messen möchten. Es eignet sich für die meisten allgemeinen Aufgaben, insbesondere wenn die Datenpunkte gleichmäßig verteilt und räumlich miteinander verbunden sind.
• Kosinusdistanz: Gute Wahl für Text- oder hochdimensionale spärliche Daten, bei denen der Winkel zwischen Vektoren wichtiger ist als die Größe. Es ist nützlich, um die Richtung in den Daten zu vergleichen.
• Manhattan-Distanz: Ideal, wenn die Datenpunkte auf einem Gitter oder Raster liegen (z. B. Stadtblöcke). Dies ist weniger empfindlich gegenüber Ausreißern als die euclidische Distanz.
• Chebyshev-Distanz: Geeignet für Situationen, in denen Bewegung in jede Richtung erfolgen kann (z.B. Schachbrett-Distanzen). Sie ist nützlich für diskrete Räume, in denen wir die maximale Achsendifferenz priorisieren möchten.
• Topologie (TOPOLOGY): In einem Gitter können Neuronen in einer hexagonalen oder rechteckigen Struktur angeordnet werden: 
• Rechteckig (Standard): Jeder Neuron hat 4 unmittelbare Nachbarn. Dies ist die richtige Wahl, wenn die Daten keine klare räumliche Beziehung haben. Es ist auch rechnerisch einfacher.
• Sechseckig: Jeder Neuron hat 6 Nachbarn. Dies ist die bevorzugte Option, wenn die Daten räumliche Beziehungen besser mit einem hexagonalen Gitter dargestellt werden. Dies ist der Fall bei kreisförmigen oder winkelbasierten Datenverteilungen.
• Anzahl der Trainingsiterationen (N_ITERATIONS): Grundsätzlich führen längere Trainingszeiten zu geringeren Fehlern und einer besseren Anpassung der Gewichte an die Eingabedaten. Allerdings steigt die Leistung des Modells asymptotisch mit der Anzahl der Iterationen. Nach einer bestimmten Anzahl von Iterationen ist der Leistungszuwachs durch nachfolgende Interaktionen nur marginal. Die Entscheidung über die richtige Anzahl von Iterationen erfordert einige Experimente. In diesem Tutorial trainieren wir das Modell über 5000 Iterationen. 

Um die richtige Konfiguration der Hyperparameter zu bestimmen, empfehlen wir, mit verschiedenen Optionen an einem kleineren Datensatz zu experimentieren.

Fazit

Selbstorganisierende Karten sind ein robustes Werkzeug für unüberwachtes Lernen. Sie werden für Clustering, Dimensionsreduktion, Anomalieerkennung und Datenvisualisierung verwendet. Da sie die topologischen Eigenschaften hochdimensionaler Daten bewahren und diese auf einem niederdimensionalen Gitter darstellen, erleichtern SOMs die Visualisierung und Interpretation komplexer Datensätze.

Dieses Tutorial behandelte die zugrunde liegenden Prinzipien von SOMs und zeigte, wie man ein SOM mit der MiniSom-Python-Bibliothek implementiert. Es demonstrierte auch, wie man die Ergebnisse visuell analysiert und erklärte die wichtigen Hyperparameter, die verwendet werden, um SOMs zu trainieren und deren Leistung zu optimieren.