Mappe Auto-Organizzanti: Una Guida Intuitiva con Esempi in Python

Impostazione dell’ambiente per le SOM

Prima di costruire il SOM, dobbiamo preparare l’ambiente con i pacchetti necessari.

Installazione delle librerie Python

Abbiamo bisogno di questi pacchetti:

• MiniSom è uno strumento Python basato su NumPy che crea e addestra i SOM.
• NumPy è utilizzato per accedere a funzioni matematiche come la suddivisione degli array, l’ottenimento di valori unici, ecc.
• matplotlib è usato per tracciare vari grafici e diagrammi per visualizzare i dati.
• Il pacchetto datasets di sklearn è utilizzato per importare i dataset su cui applicare il SOM. 
• Il pacchetto MinMaxScaler di sklearn normalizza il dataset. 

Il seguente frammento di codice importa questi pacchetti: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Preparazione del dataset

In questo tutorial, utilizziamo MiniSom per costruire un SOM e poi addestrarlo sul dataset IRIS. Questo dataset è composto da 3 classi di piante di iris. Ogni classe ha 50 istanze. Per preparare i dati, seguiamo questi passaggi: 

• Importa il dataset Iris da sklearn, 
• Estrai i vettori dei dati e gli scalari target. 
• Normalizza i vettori di dati. In questo tutorial, utilizziamo il MinMaxScaler di scikit-learn. 
• Dichiarare un insieme di etichette per ciascuna delle tre classi di piante Iris.

Il seguente codice implementa questi passaggi:

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Implementazione delle Mappe Auto-Organizzanti (SOM) in Python

Per implementare una SOM in Python, definiamo e inizializziamo la griglia prima di addestrarla sul dataset. Possiamo quindi visualizzare i neuroni addestrati e il dataset raggruppato.

Definizione della griglia SOM

Come spiegato in precedenza, un SOM è una griglia di neuroni. Utilizzando MiniSom, possiamo creare griglie bidimensionali. Le dimensioni X e Y della griglia sono il numero di neuroni lungo ciascun asse. Per definire la griglia SOM, dobbiamo anche specificare:

• Le dimensioni X e Y della griglia
• Il numero di variabili di input – questo è il numero di righe di dati.

Dichiara questi parametri come costanti Python:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

Il codice di esempio qui sotto illustra come dichiarare la griglia utilizzando MiniSom:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

I primi due parametri sono il numero di neuroni lungo gli assi X e Y, e il terzo parametro è il numero di variabili.

Dichiareremo altri parametri e iperparametri mentre creiamo la griglia SOM. Spiegheremo questi aspetti più avanti nel tutorial. Per ora, dichiara questi parametri come mostrato di seguito:

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Crea un SOM utilizzando questi parametri:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Inizializzazione dei neuroni

Il comando sopra crea un SOM con pesi casuali per tutti i neuroni. Inizializzare i neuroni con pesi tratti dai dati (invece di numeri casuali) può rendere il processo di addestramento più efficiente.

Quando si utilizza MiniSom per creare una Mappa Auto-Organizzante (SOM), ci sono due modi per inizializzare i pesi dei neuroni in base ai dati:

• Inizializzazione casuale: I pesi iniziali dei neuroni sono estratti casualmente dai dati di input. Lo facciamo applicando la .random_weights_init() funzione al SOM. 
• Inizializzazione PCA: L’inizializzazione tramite Analisi delle Componenti Principali (PCA) utilizza le componenti principali dei dati di input per inizializzare i pesi. I pesi iniziali dei neuroni coprono le prime due componenti principali. Questo porta spesso a una convergenza più rapida. 

In questa guida, utilizziamo l’inizializzazione PCA. Per applicare l’inizializzazione PCA sui pesi SOM, usa la funzione .pca_weights_init() come mostrato di seguito:

som.pca_weights_init(data)

Addestramento del SOM

Il processo di addestramento aggiorna i pesi SOM per minimizzare la distanza tra i neuroni e i punti dati.

Di seguito, spieghiamo il processo di addestramento iterativo:

• Inizializzazione: I vettori di peso di tutti i neuroni vengono inizializzati, solitamente con valori casuali. È anche possibile inizializzare i pesi campionando la distribuzione dei dati di input.
• Selezione dell’input: Un vettore di input viene (scelto casualmente) dal dataset di addestramento.
• Identificazione della BMU: Il neurone con il vettore di peso più vicino al vettore di input è identificato come la BMU.
• Aggiornamento del quartiere: Il BMU e i suoi neuroni adiacenti aggiornano i loro vettori di peso. Il tasso di apprendimento e la funzione di vicinato decidono quali neuroni vengono aggiornati e di quanto. Al passo di iterazione t, dato il vettore di input x, il vettore di peso del neurone i è w_i, il tasso di apprendimento (t), e la funzione di vicinato h_bi (questa funzione quantifica l’estensione dell’aggiornamento per il neurone i dato il neurone BMU b), la formula per l’aggiornamento del peso per il neurone i è espressa come:
• Tasso di decadimento del tasso di apprendimento e raggio di vicinanza: Sia il tasso di apprendimento che il raggio di vicinanza diminuiscono nel tempo. Nelle prime iterazioni, il processo di addestramento apporta aggiustamenti maggiori su un’area più ampia. Le iterazioni successive aiutano a perfezionare i pesi apportando cambiamenti minori ai pesi dei neuroni adiacenti. Questo consente alla mappa di stabilizzarsi e convergere. 

Per addestrare il SOM, presentiamo al modello i dati di input. Possiamo scegliere tra due approcci per farlo: 

• Seleziona campioni a caso dai dati di input. La .train_random() funzione implementa questa tecnica. 
• Esegui sequenzialmente i vettori nei dati di input. Questo viene fatto utilizzando la .train_batch() funzione. 

Queste funzioni accettano i dati di input e il numero di iterazioni come parametri. In questa guida, utilizziamo la .train_random() funzione. Dichiarare il numero di iterazioni come una costante e passarla alla funzione di addestramento: 

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

Dopo aver eseguito lo script e completato l’addestramento, viene visualizzato un messaggio con l’errore di quantizzazione:

quantization error: 0.05357240680504421 

L’errore di quantizzazione indica la quantità di informazioni perse quando il SOM quantizza (riduce la dimensionalità) i dati. Un grande errore di quantizzazione indica una maggiore distanza tra i neuroni e i punti dati. Significa anche che il raggruppamento è meno affidabile.

Visualizzare i neuroni SOM

Ora abbiamo un modello SOM addestrato. Per visualizzarlo, utilizziamo una mappa delle distanze (nota anche come U-matrice). La mappa delle distanze mostra i neuroni del SOM come una griglia di celle. Il colore di ciascuna cella rappresenta la sua distanza dai neuroni vicini.

La mappa delle distanze è una griglia con le stesse dimensioni del SOM. Ogni cella nella mappa delle distanze è la somma normalizzata delle distanze (euclidee) tra un neurone e i suoi vicini.

Accedi alla mappa delle distanze SOM utilizzando la funzione .distance_map(). Per generare la U-matrice, segui questi passaggi:

• Usa pyplot per creare una figura con le stesse dimensioni del SOM. In questo esempio, le dimensioni sono 8×8. 
• Traccia la mappa delle distanze utilizzando matplotlib con la funzione .pcolor() In questo esempio, utilizziamo gist_yarg come schema di colori.
• Visualizza la colorbar, un indice che mappa diversi colori a diversi valori scalari. In questo caso, poiché le distanze sono normalizzate, i valori di distanza scalari variano da 0 a 1. 

Il codice sottostante implementa questi passaggi: 

# crea la griglia
plt.figure(figsize=(8, 8))
# traccia la mappa delle distanze
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# mostra la barra dei colori
plt.colorbar()
plt.show()

In questo esempio, la matrice U utilizza uno schema di colori monotono. Può essere compreso utilizzando queste linee guida:

• Toni più chiari rappresentano neuroni vicini tra loro, mentre toni più scuri rappresentano neuroni più lontani dagli altri. 
• I gruppi di tonalità più chiare possono essere interpretati come cluster. I nodi scuri tra i cluster possono essere interpretati come i confini tra i cluster.

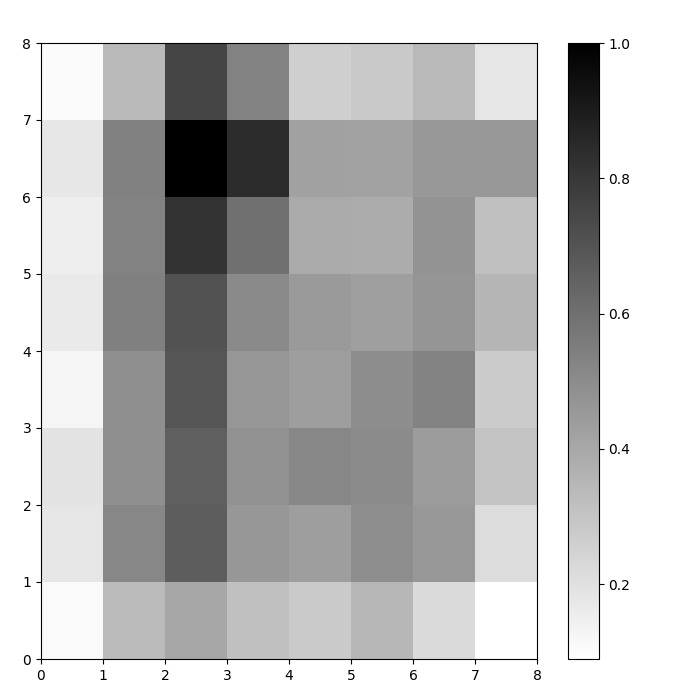
Figura 1: U-matrix di SOM addestrato sul dataset Iris (immagine dell’autore)

Valutazione dei risultati di clustering del SOM

La figura precedente ha illustrato graficamente i neuroni del SOM. In questa sezione, mostriamo come visualizzare come il SOM ha raggruppato i dati.

Identificazione dei cluster

Sovrapponiamo dei marcatori sopra la U-matrix sopra per indicare a quale classe di pianta Iris appartiene ciascuna cella (neurone). Per fare ciò:

• Come prima, crea una figura 8×8 utilizzando pyplot, tracciando la mappa delle distanze e mostrando la barra dei colori. 
• Specifica un array di tre marker di matplotlib, uno per ciascuna classe di pianta Iris. 
• Specifica un array di tre colori di matplotlib, uno per ogni classe di pianta Iris. 
• Traccia iterativamente il neurone vincente per ciascun punto dati:
• Determina le (coordinate del) neurone vincente per ogni punto dati utilizzando la .winner() funzione. 
• Traccia la posizione di ogni neurone vincente nel mezzo di ciascuna cella sulla griglia. w[0] e w[1] forniscono le coordinate X e Y del neurone, rispettivamente. Un valore di 0.5 viene aggiunto a ciascuna coordinata per tracciarlo nel mezzo della cella. 

Il codice sottostante mostra come fare:

# traccia la mappa delle distanze
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# crea i marcatori e i colori per ciascuna classe
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# traccia il neurone vincente per ogni punto dati
for count, datapoint in enumerate(data):
    # ottieni il vincitore
    w = som.winner(datapoint)  
    # posiziona un marcatore sulla posizione vincente per il punto dati campione
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

L’immagine risultante è mostrata di seguito:

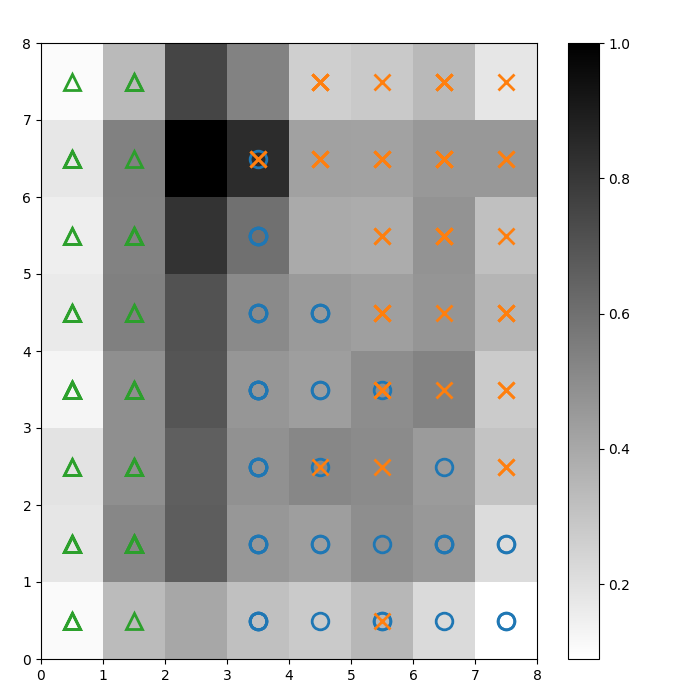
Figura 2: U-matrice sovrapposta con i marcatori di classe (immagine dell’autore)

Basato sulla documentazione del dataset Iris, “una classe è linearmente separabile dalle altre 2; quest’ultime non sono linearmente separabili tra loro”. Nella U-matrice sopra, queste tre classi sono rappresentate da tre marcatori – triangolo, cerchio e croce.

Nota che non c’è un confine chiaro tra i cerchi blu e le croci arancioni. Inoltre, due classi sono sovrapposte allo stesso neurone in molte celle. Questo significa che il neurone è equidistante da entrambe le classi.

Visualizzare il risultato del clustering

Un SOM è un modello di clustering. Punti dati simili si mappano allo stesso neurone. I punti dati della stessa classe si mappano a un cluster di neuroni vicini. Tracciamo tutti i punti dati sulla griglia SOM per studiare meglio il comportamento del clustering.

I seguenti passaggi descrivono come creare questo diagramma a dispersione:

• Ottieni le coordinate X e Y del neurone vincente per ciascun punto dati.
• Traccia la mappa delle distanze, come abbiamo fatto per Figura 1.
• Utilizza plt.scatter() per creare un grafico a dispersione di tutti i neuroni vincenti per ciascun punto dati. Aggiungi un offset casuale a ciascun punto per evitare sovrapposizioni tra i punti dati all’interno della stessa cella.

Implementiamo questi passaggi nel codice seguente: 

# ottieni le coordinate X e Y del neurone vincente per ciascun punto datiw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# traccia la mappa delle distanze
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# crea un grafico a dispersione di tutti i neuroni vincenti per ciascun punto dati
# aggiungi un offset casuale a ciascun punto per evitare sovrapposizioni
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

Il seguente grafico mostra il grafico a dispersione dell’output:

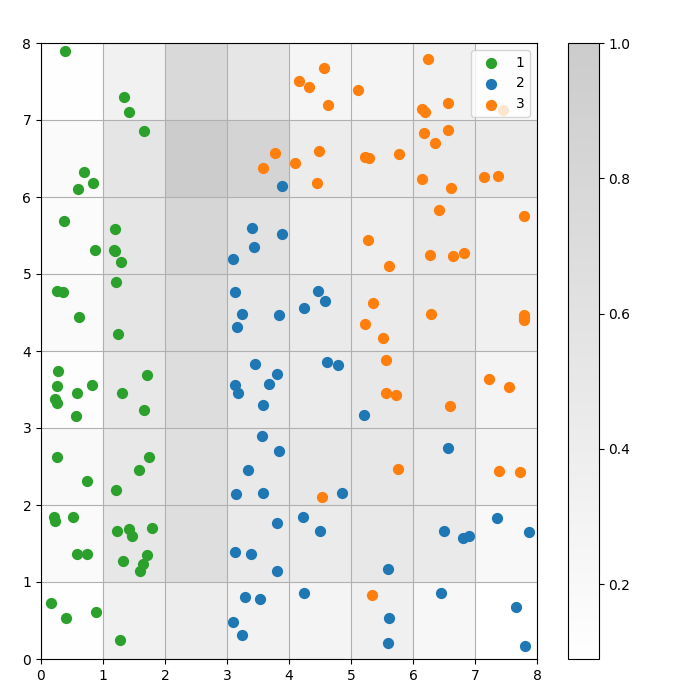Figura 3: Diagramma a dispersione dei punti dati all’interno delle celle (immagine dell’autore)

Nel diagramma a dispersione sopra, osserva che: 

• Alcune celle contengono sia punti blu che arancioni. 
• I punti verdi sono chiaramente separati dal resto dei dati, ma i punti blu e arancioni non sono separati in modo netto. 
• Le osservazioni sopra sono in linea con il fatto che solo uno dei tre cluster nel dataset Iris ha un confine chiaro.
• In Figura 1, i nodi scuri tra i cluster (che possono essere interpretati come i confini tra i cluster) corrispondono a celle vuote nel diagramma a dispersione.

Puoi accedere e eseguire il codice completo su questo notebook DataLab.

Ottimizzazione del Modello SOM

Le sezioni precedenti hanno mostrato come creare e addestrare un modello SOM e come studiare i risultati visivamente. In questa sezione, discuteremo come ottimizzare le prestazioni dei modelli SOM.

Hyperparametri chiave da ottimizzare

Come con qualsiasi modello di apprendimento automatico, gli iperparametri influenzano notevolmente le prestazioni del modello.

Alcuni degli iperparametri importanti nell’addestramento degli SOM sono:

• La dimensione della griglia determina la dimensione della mappa. Il numero di neuroni in una mappa con una dimensione della griglia di AxB è A*B.
• Il tasso di apprendimento determina quanto vengono modificati i pesi in ogni iterazione. Impostiamo il tasso di apprendimento iniziale, che diminuisce nel tempo secondo la funzione di decadimento.
• La funzione di decadimento decide l’estensione con cui il tasso di apprendimento viene ridotto in ogni iterazione successiva.
• La funzione di vicinato è una funzione matematica che specifica quali neuroni devono essere considerati come i vicini del BMU.
• La deviazione standard specifica la diffusione della funzione di vicinato. Ad esempio, una funzione di vicinato gaussiana con una alta deviazione standard avrà un vicinato più grande rispetto alla stessa funzione con una deviazione standard più bassa. Impostiamo la deviazione standard iniziale, che diminuisce nel tempo secondo la funzione di decadimento sigma.
• La funzione di decadimento sigma controlla quanto viene ridotta la deviazione standard in ogni iterazione successiva. 
• Il numero di iterazioni di addestramento determina quante volte i pesi vengono aggiornati. In ogni iterazione di addestramento, i pesi dei neuroni vengono aggiornati una volta. 
• La funzione distanza è una funzione matematica che calcola la distanza tra neuroni e punti dati. 
• La topologia determina il layout della struttura della griglia. I neuroni nella griglia possono essere disposti in un modello rettangolare o esagonale. 

Nella sezione successiva, discutiamo le linee guida per impostare i valori di questi iperparametri. 

Impatto della sintonizzazione degli iperparametri

I valori degli iperparametri dovrebbero essere decisi in base al modello e al dataset. Fino a un certo punto, determinare questi valori è un processo di tentativi ed errori. In questa sezione, forniamo indicazioni per la regolazione di ciascun iperparametro. Accanto a ciascun iperparametro, menzioniamo (tra parentesi) le rispettive costanti Python utilizzate nel codice di esempio.

• Dimensione della griglia (SOM_X_AXIS_NODES e SOM_X_AXIS_NODES): La dimensione della griglia dipende dalla dimensione del dataset. La regola generale è che dato un dataset di dimensione N, la griglia dovrebbe contenere approssimativamente 5*sqrt(N) neuroni. Ad esempio, se il dataset ha 150 campioni, la griglia dovrebbe contenere 5*sqrt(150) = circa 61 neuroni. In questo tutorial, il dataset Iris ha 150 righe e utilizziamo una griglia 8×8. 
• Velocità di apprendimento iniziale (ALPHA): Una velocità più alta accelera la convergenza, mentre velocità più basse vengono utilizzate per aggiustamenti più fini dopo le prime iterazioni. La velocità di apprendimento iniziale dovrebbe essere sufficientemente grande per consentire un rapido adattamento, ma non così grande da superare i valori ottimali dei pesi. In questo articolo, la velocità di apprendimento iniziale è 0,5. 
• Deviazione standard iniziale (SIGMA0): Determina la dimensione o la diffusione iniziale del vicinato. Un valore più grande considera modelli più globali. In questo esempio, utilizziamo una deviazione standard iniziale di 1,5. 
• Per il tasso di decadimento (DECAY_FUNC) e il tasso di decadimento sigma (SIGMA_DECAY_FUNC), possiamo scegliere tra uno dei tre tipi di funzioni di decadimento: 
• Decadimento inverso: Questa funzione è adatta se i dati presentano sia schemi globali che locali. In tali casi, è necessario un periodo più lungo di apprendimento ampio prima di concentrarsi sugli schemi locali. 
• Decadimento lineare: Questo è buono per i dataset in cui vogliamo una dimensione del vicinato o una riduzione del tasso di apprendimento costante e uniforme. Questo è utile se i dati non necessitano di molte regolazioni.
• Decadimento asintotico: Questa funzione è utile se i dati sono complessi e ad alta dimensione. In tali casi, è meglio dedicare più tempo all’esplorazione globale prima di passare gradualmente ai dettagli più fini. 
• Funzione di vicinato (NEIGHBORHOOD_FUNC): La scelta predefinita della funzione di vicinato è la funzione gaussiana. Altre funzioni, come spiegato di seguito, sono utilizzate anch’esse. 
• Gaussiana (predefinita): Questa è una curva a campana. L’estensione con cui un neurone viene aggiornato diminuisce gradualmente man mano che aumenta la sua distanza dal neurone vincente. Fornisce una transizione fluida e continua e preserva la topologia dei dati. È adatta per la maggior parte degli scopi generali grazie al suo comportamento stabile e prevedibile.
• Bubble: Questa funzione crea un vicinato a larghezza fissa. Tutti i neuroni all’interno di questo vicinato vengono aggiornati in modo uniforme, mentre i neuroni al di fuori di questo vicinato non vengono aggiornati (per un dato punto). È computazionalmente più economico e più facile da implementare. È utile per mappe più piccole dove confini di vicinato netti non compromettono un clustering efficace. 
• Cappello messicano: Ha una regione centrale positiva circondata da una regione negativa. I neuroni vicini al BMU vengono aggiornati per avvicinarsi al punto dati, e i neuroni più lontani vengono aggiornati per allontanarsi dal punto dati. Questa tecnica migliora il contrasto e affina le caratteristiche nella mappa. Poiché enfatizza cluster distinti, è efficace nei compiti di riconoscimento dei modelli dove è desiderata una chiara separazione dei cluster.
• Triangolo: Questa funzione definisce la dimensione del vicinato come un triangolo, con il BMU che ha la maggiore influenza. Diminuisce linearmente con la distanza dal BMU. È utilizzata per raggruppare dati con transizioni graduali tra cluster o caratteristiche, come dati di immagini, di parlato o serie temporali, dove i punti dati vicini si prevede condividano caratteristiche simili.
• Funzione di distanza (DISTANCE_FUNC): Per misurare la distanza tra neuroni e punti dati, possiamo scegliere tra 4 metodi:
• Distanza euclidea (scelta predefinita): Utile quando i dati sono continui e vogliamo misurare la distanza in linea retta. Si adatta alla maggior parte delle attività generali, specialmente quando i punti dati sono distribuiti uniformemente e correlati spazialmente.
• Distanza coseno: Buona scelta per dati testuali o dati sparsi ad alta dimensione in cui l’angolo tra i vettori è più importante della magnitudine. È utile per confrontare la direzionalità nei dati.
• Distanza di Manhattan: Ideale quando i punti dati si trovano su una griglia o reticolo (ad es., isolati urbani). Questo è meno sensibile agli outlier rispetto alla distanza euclidea.
• Distanza di Chebyshev: Adatta per situazioni in cui il movimento può avvenire in qualsiasi direzione (ad esempio, distanze da scacchiera). È utile per spazi discreti dove vogliamo dare priorità alla massima differenza sugli assi.
• Topologia (TOPOLOGIA): In una griglia, i neuroni possono essere disposti in una struttura esagonale o rettangolare: 
• Retangolare (predefinito): ogni neurone ha 4 vicini immediati. Questa è la scelta giusta quando i dati non hanno una chiara relazione spaziale. È anche computazionalmente più semplice.
• Esagonale: ogni neurone ha 6 vicini. Questa è l’opzione preferita se i dati hanno relazioni spaziali meglio rappresentate con una griglia esagonale. Questo è il caso per distribuzioni di dati circolari o angolari.
• Numero di iterazioni di addestramento (N_ITERATIONS): In linea di principio, tempi di addestramento più lunghi portano a errori più bassi e a un migliore allineamento dei pesi con i dati di input. Tuttavia, le prestazioni del modello aumentano asintoticamente con il numero di iterazioni. Pertanto, dopo un certo numero di iterazioni, l’aumento delle prestazioni derivante dalle interazioni successive è solo marginale. Decidere il numero corretto di iterazioni richiede un po’ di sperimentazione. In questo tutorial, addestriamo il modello per 5000 iterazioni. 

Per determinare la giusta configurazione degli iperparametri, raccomandiamo di sperimentare con varie opzioni su un sottoinsieme più piccolo dei dati.

Conclusione

Le mappe auto-organizzanti sono uno strumento robusto per l’apprendimento non supervisionato. Vengono utilizzate per il clustering, la riduzione della dimensionalità, la rilevazione di anomalie e la visualizzazione dei dati. Poiché preservano le proprietà topologiche dei dati ad alta dimensione e li rappresentano su una griglia a dimensione inferiore, le SOM rendono facile visualizzare e interpretare set di dati complessi.

Questo tutorial ha discusso i principi sottostanti delle SOM e ha mostrato come implementare una SOM utilizzando la libreria Python MiniSom. Ha anche dimostrato come analizzare visivamente i risultati e ha spiegato i principali iperparametri utilizzati per addestrare le SOM e ottimizzare le loro prestazioni.