自己組織化マップ：Pythonの例を用いた直感的ガイド

チュートリアル
Python

自己組織化マップ（SOM）は、教師なし学習タスク、例えばクラスタリングに使用される人工ニューラルネットワークの一種です。データポイントのセットが与えられると、モデルはデータをクラスタに分割することを学習します。SOMは、複雑な多次元データを低次元（通常は2次元）のグリッドに投影します。これにより、視覚化が容易になります。したがって、SOMは高次元データを視覚化するためにも使用されます。

このチュートリアルでは、SOMの基本概念、その学習プロセス、および一般的な使用例を探ります。PythonでMiniSomライブラリを使用して結果を視覚的に表現する方法を説明します。最後に、SOMモデルのトレーニングにおける重要なハイパーパラメータと、それらを微調整する方法について説明します。

自己組織化マップ（SOM）の理解

このセクションでは、SOMのコア概念、学習プロセス、および使用例を紹介します。

SOMのコア概念

自己組織化マップには理解するために重要な一連の概念が含まれています。

ニューロン

SOMは本質的にニューロンのグリッドです。トレーニング中、入力データポイントに最も近い重みベクトルを持つニューロンが、その重みと隣接するニューロンの重みを調整し、入力データポイントにさらに近づけます。多くの反復を経て、隣接するニューロンのグループが関連するデータポイントにマッピングされます。これにより、入力データセットのクラスタリングが行われます。

グリッド構造

SOMのニューロンはグリッドとして組織されています。隣接するニューロンは類似したデータポイントにマッピングされます。大きなデータセットにはより大きなグリッドが必要です。通常、このグリッドは二次元です。グリッド構造は、高次元データがマッピングされる低次元空間として機能します。グリッドはデータパターンやクラスタを視覚化するのに役立ちます。

データポイントのマッピング

各データポイントは、距離指標を使用してすべてのニューロンと比較されます。入力データポイントに最も近い重みベクトルを持つニューロンが、そのデータポイントに対する最適一致ユニット（BMU）です。

BMUが特定されると、BMUとその隣接ニューロンの重みが更新されます。この更新により、BMUと隣接ニューロンは入力データポイントにさらに近づきます。このマッピングはデータのトポロジーを保持し、類似のデータポイントが近くのニューロンにマッピングされることを保証します。

自己組織化マップの学習プロセス

自己組織化マップのトレーニングは無監督と見なされますラベル付きデータセットに基づいていないためです。自己組織化マップをトレーニングする目的は、ニューロンの重みベクトルを反復的に調整し、類似のデータポイントが近くのニューロンにマッピングされるようにすることです。

競争学習

SOMは、競争学習を使用します（勾配降下法やバックプロパゲーションの代わりに）。ニューロンは各入力データポイントに対する最適一致ユニット（BMU）になるために競い合います。データポイントに最も近いニューロンがそのBMUとして決定されます。BMUおよびその隣接ニューロンは、データポイントとの距離をさらに減少させるために更新されます。隣接ニューロンは関連するデータポイントにマッピングされます。これにより、ニューロン間の専門化と入力データポイントのクラスタリングが促進されます。

距離関数

SOMは、ニューロンとデータポイント間の距離を測定するために距離関数を使用します。この距離は各データポイントのBMUを決定するために使用されます。MiniSomには、選択できる4つの距離関数があります：

近傍関数

データポイントのBMUを特定した後、BMUとその隣接ニューロンはそのデータポイントの方向に更新されます。近傍関数はSOMが入力データのトポロジカルな関係を維持することを保証します。近傍関数は次のことを決定します：

  • どのニューロンがBMUの近傍にあると見なされるか
  • 隣接ニューロンがどの程度更新されるか。一般的に、BMUに近いニューロンは、遠くにあるニューロンよりも大きな調整を受けます

MiniSomには3つの近傍関数があります：

  • ガウス（これがデフォルトです）。
  • バブル
  • メキシカンハット
  • トライアングル

反復プロセス

SOMの学習プロセスは、いくつかの反復を経て行われます。各反復では、SOMは多くの入力データポイントを処理します。以下のステップで学習プロセスを概説します：

  • トレーニングが始まると、すべてのニューロンの重みは（ランダムに）初期化されます。
  • 入力データポイントが与えられると、各ニューロンは入力からの距離を計算します。
    • 最も距離が小さいニューロンがBMU（Best Matching Unit）として宣言されます。
  • BMUとその近隣の重みは、入力ベクトルに近づくように調整されます。この調整の程度は次のように決定されます：
    • 近隣関数：BMUから遠く離れたニューロンは、BMUに近いニューロンよりも少なく更新されます。これによりデータの位相構造が保持されます。
    • 学習率：高い学習率は、より大きな更新をもたらします。

これらのステップは、多くの反復を経て繰り返され、多くの入力データポイントを通過します。重みは徐々に更新され、マップが自己組織化し、データの構造を捉えます。

学習率と近傍半径は通常、時間とともに減少し、SOMが重みを徐々に微調整できるようにします。チュートリアルの後半では、Pythonコードを使用して反復トレーニングプロセスのステップを実装します。

SOMの典型的な使用例

SOMはその独自のアーキテクチャにより、機械学習、分析、視覚化においていくつかの典型的なアプリケーションを持っています。

クラスタリング

SOMは、高次元データを類似したデータポイントのクラスターにグループ化するために使用されます。これにより、データ内の固有の構造を特定するのに役立ちます。各ニューロンは密接に関連するデータポイントにマッピングされ、類似したデータポイントは同じまたは隣接するニューロンにマッピングされるため、明確なクラスターが形成されます。

たとえば、マーケティングにおいて、SOMは購入行動に基づいて顧客をグループ化することができます。これにより、ブランドは異なる顧客セグメント（クラスター）に合わせてマーケティング戦略を調整することができます。

次元削減

SOMは、多くの特徴ベクトルを持つ高次元データを、次元数の少ないグリッド（通常は2次元グリッド）にマッピングできます。このマッピングはデータポイント間の関係を保持するため、次元が削減されることで、情報の重要な損失なしに複雑なデータセットを視覚化しやすくなります。

SOMは、視覚化と分析作業を容易にするだけでなく、他の機械学習アルゴリズムを適用する前にデータの次元を削減することもできます。SOMは、類似した特性を持つピクセルや領域をクラスタリングすることで特徴数を減らすために画像処理にも使用され、画像認識や分類作業をより効率的にします。

異常検知

トレーニングプロセス中、ほとんどのデータポイントは特定のニューロンにマッピングされます。異常（どのクラスタにも適合しないデータポイント）は通常、遠くまたは人口が少ないニューロンにマッピングされます。これらの外れ値は学習されたクラスタに適合せず、通常のデータポイントのBMUから遠くのニューロンにマッピングされます。

例えば、SOMグリッド上に金融取引をマッピングすることで、潜在的に詐欺的な活動を示す異常な活動（外れ値）を特定することができます。

データ視覚化

データ可視化は、SOMの最も一般的なユースケースの1つです。高次元データは可視化が困難です。SOMはデータの次元を削減し、2次元グリッドに投影することで、可視化を容易にします。これにより、データ内のクラスターや、元のデータでは発見が難しい異常なデータポイントを検出するのにも役立ちます。

例えば、データ可視化は高次元の人口データを分析するのを容易にします。データを2Dグリッドにマッピングすることで、異なる人口グループ間の類似点や違いを見つけるのに役立ちます。

SOMの基本概念とユースケースについて説明した後、次のセクションでは、PythonパッケージMiniSomを使用してそれらを実装する方法を示します。

完全なコードにアクセスして実行するには、このDataLabノートブックをご覧ください。

SOMのための環境設定

SOMを構築する前に、必要なパッケージで環境を整える必要があります。

Pythonライブラリのインストール

これらのパッケージが必要です：

  • MiniSomは、SOMを作成し、訓練するためのNumPyベースのPythonツールです。
  • NumPyは、配列の分割やユニークな値の取得などの数学関数にアクセスするために使用されます。
  • matplotlibは、データを視覚化するためにさまざまなグラフやチャートをプロットするために使用されます。
  • データセットに適用するためのdatasetsパッケージはsklearnからインポートされます。
  • MinMaxScalerパッケージはsklearnからデータセットを正規化します。

以下のコードスニペットはこれらのパッケージをインポートします：

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

データセットの準備

このチュートリアルでは、MiniSomを使用してSOMを構築し、次にそれを 標準 IRISデータセット に対してトレーニングします。このデータ セットは、3つのアイリス植物のクラスで構成されています。各クラスには50のインスタンスがあります。データを準備するために、次の手順に従います：

  • コードからアイリスデータセットをインポートする sklearn、
  • データベクトルとターゲットスカラーを抽出します。
  • データベクトルを正規化します。このチュートリアルでは、 scikit-learnのMinMaxScaler
  • アイリス植物の3つのクラスごとにラベルのセットを宣言します。

次のコードはこれらのステップを実装します：

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Pythonでの自己組織化マップ（SOM）の実装

PythonでSOMを実装するには、データセットで学習する前にグリッドを定義し初期化します。その後、学習したニューロンとクラスタリングされたデータセットを視覚化できます。

SOMグリッドの定義

前述のように、SOMはニューロンのグリッドです。MiniSomを使用すると、2次元のグリッドを作成できます。グリッドのXおよびY次元は、それぞれの軸に沿ったニューロンの数です。SOMグリッドを定義するには、以下も指定する必要があります：

  • グリッドのXおよびY次元
  • 入力変数の数 – これはデータ行の数です。

これらのパラメータをPythonの定数として宣言します：

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

以下のサンプルコードは、MiniSomを使用してグリッドを宣言する方法を示しています：

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

最初の2つのパラメータはXおよびY軸に沿ったニューロンの数で、3番目のパラメータは変数の数です。

私たちはSOMグリッドを作成する際に、他のパラメータとハイパーパラメータを宣言します。これらについては後でチュートリアルで説明します。とりあえず、以下のようにこれらのパラメータを宣言してください：

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

これらのパラメータを使用してSOMを作成します：

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

ニューロンの初期化

上記のコマンドは、すべてのニューロンの重みをランダムに設定したSOMを作成します。データから引き出した重みでニューロンを初期化することで（ランダムな数値の代わりに）、トレーニングプロセスがより効率的になる可能性があります。

MiniSomを使用して自己組織化マップ（SOM）を作成する際に、データに基づいてニューロンの重みを初期化する方法は2つあります：

  • ランダム初期化: ニューロンの初期重みは入力データからランダムに抽出されます。これは、.random_weights_init()関数をSOMに適用することで行います。
  • PCA初期化: 主成分分析（PCA）初期化は、入力データの主成分を使用して重みを初期化します。ニューロンの初期重みは最初の二つの主成分にまたがります。これにより、収束が速くなることがよくあります。

このガイドでは、PCA初期化を使用します。SOMの重みへのPCA初期化を適用するには、以下に示すように.pca_weights_init()関数を使用します:

som.pca_weights_init(data)

SOMのトレーニング

トレーニングプロセスでは、ニューロンとデータポイントの距離を最小限に抑えるためにSOMの重みが更新されます。

以下に、反復トレーニングプロセスを説明します:

  • 初期化: すべてのニューロンの重みベクトルは、通常ランダムな値で初期化されます。また、入力データの分布をサンプリングすることで重みを初期化することも可能です。
  • 入力選択: 入力ベクトルはトレーニングデータセットから（ランダムに）選択されます。
  • BMU識別: 入力ベクトルに最も近い重みベクトルを持つニューロンがBMUとして識別されます。
  • 近隣の更新: BMUとその隣接ニューロンは、重みベクトルを更新します。学習率と近隣関数は、どのニューロンがどの程度更新されるかを決定します。イテレーションステップ tにおいて、入力ベクトル x、ニューロン i の重みベクトルを wi、学習率 (t)、および近隣関数 hbi（この関数はBMUニューロン b に対してニューロン i の更新の程度を定量化します）、ニューロン i の重み更新の公式は次のように表されます:
  • 学習率と隣接半径の減衰率: 学習率と隣接半径は時間と共に減少します。初期の反復では、トレーニングプロセスがより大きな隣接範囲に対して大きな調整を行います。後の反復では、隣接するニューロンの重みの小さな変更を行うことで重みを微調整します。これにより、マップは安定し、収束します。

SOMをトレーニングするために、モデルに入力データを提示します。これを行うために、2つのアプローチのいずれかを選択できます：

  • 入力データからランダムにサンプルを選びます。.train_random()関数はこの技術を実装しています。
  • 入力データ内のベクトルを順次実行します。これは.train_batch() 関数を使用して行います。

これらの関数は、入力データと反復回数をパラメータとして受け取ります。このガイドでは、.train_random() 関数を使用します。反復回数を定数として宣言し、それを訓練関数に渡します：

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)

スクリプトを実行し、訓練を完了すると、量子化誤差を含むメッセージが表示されます：

quantization error: 0.05357240680504421

量子化誤差は、SOMがデータを量子化（次元を削減）する際に失われる情報量を示します。大きな量子化誤差は、ニューロンとデータポイントの間の距離が大きいことを示します。また、クラスタリングの信頼性が低いことも意味します。

視覚化されたSOMニューロン

私たちは今、訓練されたSOMモデルを持っています。それを視覚化するために、距離マップ（ Uマトリックスとも呼ばれます）を使用します。距離マップは、SOMのニューロンをセルのグリッドとして表示します。各セルの色は、隣接するニューロンとの距離を表します。

距離マップは、SOMと同じ次元のグリッドです。距離マップの各セルは、ニューロンとその隣接ニューロンとの（ユークリッド）距離の正規化された合計です。

距離マップをSOM distance map関数.distance_map()を使用してアクセスします。Uマトリックスを生成するために、以下の手順に従います：

  • 同じサイズの図を作成するためにpyplotを使用します。この例では、サイズは8×8です。
  • 距離マップをmatplotlibを使用してプロットし、.pcolor()関数を使用します。この例では、gist_yarg をカラースキームとして使用します。
  • 色の異なるスカラー値をマッピングするインデックスであるcolorbarを表示します。この場合、距離が正規化されているため、スカラー距離値は0から1の範囲になります。

以下のコードはこれらのステップを実装しています：

# グリッドを作成
plt.figure(figsize=(8, 8))
# 距離マップをプロット
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# カラーバーを表示
plt.colorbar()
plt.show()

この例では、Uマトリックスは単調なカラースキームを使用しています。これらのガイドラインを使って理解できます：

  • 明るい色合いは密接に配置されたニューロンを表し、暗い色合いは他のニューロンから遠く離れたニューロンを表します。
  • 明るい色合いのグループはクラスターとして解釈できます。クラスター間の暗いノードは、クラスター間の境界として解釈できます。

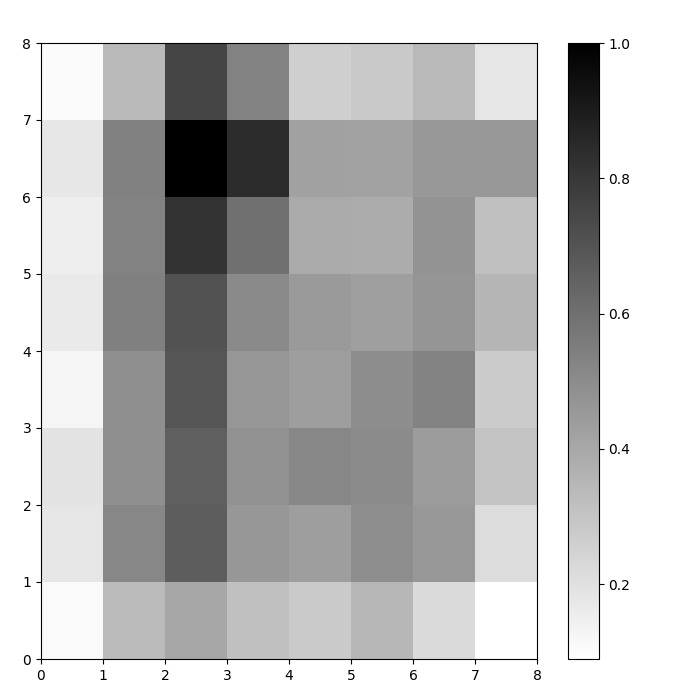
図1: アイリスデータセットで訓練されたSOMのU行列（著者による画像）

SOMクラスタリング結果の評価

前の図はSOMのニューロンをグラフィカルに示しました。このセクションでは、SOMがデータをどのようにクラスタリングしたかを視覚化する方法を示します。

クラスタの特定

上記のU行列にマーカーを重ねて、各セル（ニューロン）がどのクラスのアイリス植物を表しているかを示します。これを行うには：

  • 以前と同様に、pyplotを使用して8×8の図を作成し、距離マップをプロットし、カラーバーを表示します。
  • 3つのIris植物のクラスごとに1つずつ、matplotlibマーカーの配列を指定します。
  • 3つのmatplotlibカラーコードの配列を指定し、それぞれIris植物のクラスごとに1つずつ指定します。
  • 各データポイントの勝利ニューロンを反復的にプロットします。
    • 各データポイントの勝利ニューロンの（座標を）.winner(関数を使用して決定します。
    • 各セルの中央における勝利ニューロンの位置をプロットします。w[0]とw[1]は、それぞれニューロンのX座標とY座標を示します。各座標には0.5の値が加えられ、セルの中央にプロットされます。

以下のコードがこれを実行する方法を示しています：

# 距離マップをプロットする
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# 各クラスのマーカーと色を作成する
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# 各データポイントの勝利ニューロンをプロットする
for count, datapoint in enumerate(data):
    # 勝者を取得する
    w = som.winner(datapoint)  
    # サンプルデータポイントの勝利位置にマーカーを配置する
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

結果の画像は以下に示されています：

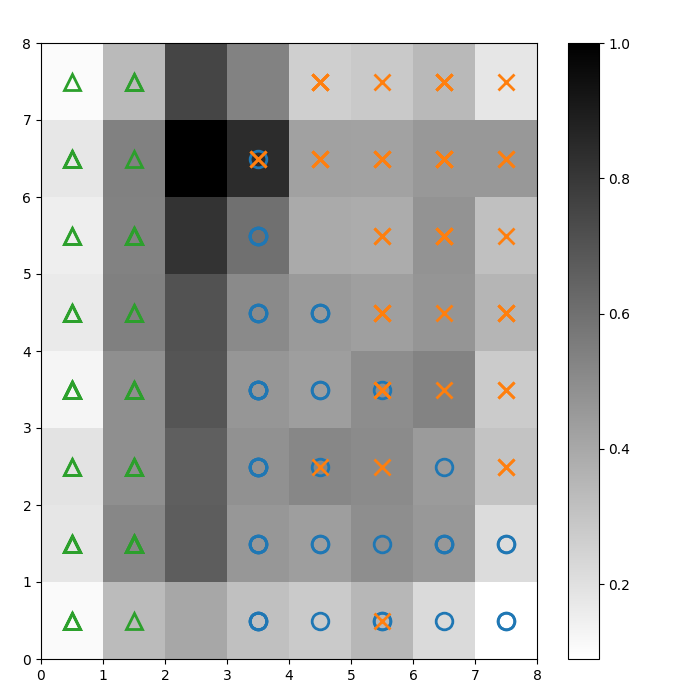
図2：クラスマーカーが重ねられたUマトリックス（著者による画像）

以下に基づいて Irisデータセットのドキュメントによると、「1つのクラスは他の2つのクラスから線形的に分離可能であり、後者は互いに線形的に分離不可能である」。上記のUマトリックスでは、これら3つのクラスは三角形、円、十字の3つのマーカーで表されています。

青い円とオレンジの十字の間に明確な境界がないことに注意してください。さらに、2つのクラスが多くのセルで同じニューロンに重なっています。これは、そのニューロンが両方のクラスから等距離にあることを意味します。

クラスタリング結果の可視化

SOMはクラスタリングモデルです。類似したデータポイントは同じニューロンにマッピングされます。同じクラスのデータポイントは隣接するニューロンのクラスタにマッピングされます。クラスタリングの挙動をより良く研究するために、すべてのデータポイントをSOMグリッド上にプロットします。

以下の手順では、この散布図を作成する方法を説明します：

  • 各データポイントの勝利ニューロンのXおよびY座標を取得します。
  • 距離マップをプロットします。これは図1のように行います。
  • すべてのデータポイントに対する勝利ニューロンの散布図を作成するには、plt.scatter()を使用します。同じセル内のデータポイント間の重なりを避けるために、各ポイントにランダムなオフセットを追加します。

以下のコードでこれらのステップを実装します：

# 各データポイントの勝利ニューロンのXおよびY座標を取得するw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# 距離マップをプロットする
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# 各データポイントの勝利ニューロンの散布図を作成する
# 重なりを避けるために各ポイントにランダムなオフセットを追加する
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

以下のグラフは出力された散布図を示しています：

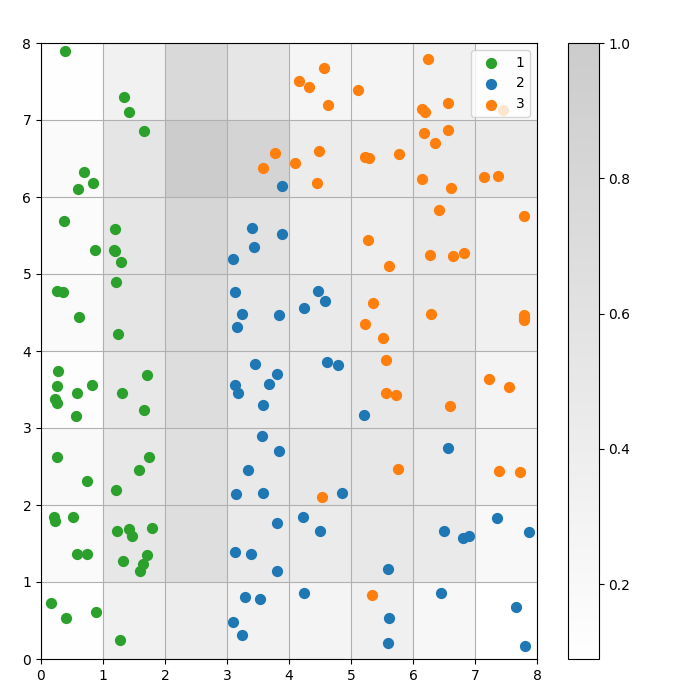図3: セル内のデータポイントの散布図（著者による画像）

上の散布図から観察できること：

  • いくつかのセルには青い点とオレンジの点が両方含まれています。
  • 緑の点は他のデータから明確に分離されていますが、青とオレンジの点はきれいに分離されていません。
  • 上記の観察は、Irisデータセットの3つのクラスタのうち、明確な境界を持つのが1つだけであるという事実と一致しています。
  • 図1では、クラスタ間の暗いノード（クラスタ間の境界として解釈できる）が散布図の空のセルと一致しています。

完全なコードはこのDataLabノートブックでアクセスして実行できます。

SOMモデルの調整

前のセクションでは、SOMモデルを作成してトレーニングする方法と、結果を視覚的に確認する方法を示しました。このセクションでは、SOMモデルのパフォーマンスを調整する方法について説明します。

調整すべき主要なハイパーパラメータ

あらゆる機械学習モデルと同様に、ハイパーパラメータはモデルのパフォーマンスに大きな影響を与えます。

SOMのトレーニングにおいて重要なハイパーパラメータは次の通りです：

  • グリッドサイズはマップのサイズを決定します。グリッドサイズがAxBのマップにおけるニューロンの数はA*Bです。
  • 学習率は各イテレーションで重みがどれだけ変更されるかを決定します。初期の学習率を設定し、減衰関数に従って時間とともに減少します。
  • 減衰関数は各後続のイテレーションで学習率がどれだけ減少するかの範囲を決定します。
  • 隣接機能は、どのニューロンがBMUの隣人と見なされるべきかを指定する数学的関数です。
  • 標準偏差は、隣接機能の広がりを指定します。たとえば、高い標準偏差を持つガウス隣接機能は、同じ機能で小さい標準偏差を持つものよりも大きな隣接領域を持ちます。初期の標準偏差を設定し、これはシグマ減衰関数に従って時間とともに減少します。
  • その シグマ減衰関数は、各反復で標準偏差がどれだけ減少するかを制御します。
  • トレーニングの 反復回数は、重みが何回更新されるかを決定します。各トレーニング反復で、ニューロンの重みは1回更新されます。
  • この距離関数は、ニューロンとデータポイント間の距離を計算する数学的関数です。
  • このトポロジーは、グリッド構造のレイアウトを決定します。グリッド内のニューロンは、長方形または六角形のパターンに配置できます。

次のセクションでは、これらのハイパーパラメータの値を設定するためのガイドラインについて説明します。

ハイパーパラメータ調整の影響

ハイパーパラメータの値は、モデルとデータセットに基づいて決定されるべきです。ある程度、これらの値を決定することは試行錯誤のプロセスです。本セクションでは、各ハイパーパラメータを調整するためのガイドラインを提供します。各ハイパーパラメータの横には、サンプルコードで使用されるそれぞれのPython定数を（括弧内に）記載します。

  • グリッドサイズ (SOM_X_AXIS_NODES と SOM_X_AXIS_NODES): グリッドサイズはデータセットのサイズに依存します。一般的な目安として、サイズNのデータセットが与えられた場合、グリッドにはおおよそ 5*sqrt(N) ニューロンが含まれるべきです。例えば、データセットに150サンプルがある場合、グリッドには 5*sqrt(150) = 約61ニューロンが含まれるべきです。このチュートリアルでは、アイリスデータセットは150行あり、8×8のグリッドを使用します。
  • 初期学習率(ALPHA): 高い学習率は収束を速めますが、低い学習率は初期の反復後に微調整に使用されます。初期の学習率は、迅速な適応を可能にするために十分に大きい必要がありますが、最適な重みの値を超えてしまうほど大きくなってはいけません。本記事では、初期学習率は0.5です。
  • 初期標準偏差(SIGMA0): 近隣の初期サイズまたは広がりを決定します。大きな値は、より多くのグローバルパターンを考慮します。この例では、初期標準偏差を1.5とします。
  • の 減衰率 (DECAY_FUNC) および シグマ減衰率 (SIGMA_DECAY_FUNC), 3種類の減衰関数から選択できます:
    • 逆減衰: この関数は、データにグローバルなパターンとローカルなパターンの両方が存在する場合に適しています。そのような場合、ローカルパターンに焦点を当てる前に、広範な学習の長いフェーズが必要です。
    • 線形減衰: これは、安定した均一な隣接サイズや学習率の減少を求めるデータセットに適しています。データがあまり微調整を必要としない場合に便利です。
    • 漸近的減衰: この関数は、データが複雑で高次元の場合に有用です。そのような場合、細かな詳細に徐々に移行する前に、グローバルな探索にもっと時間を費やす方が良いです。
  • 近傍関数 (NEIGHBORHOOD_FUNC): 近傍関数のデフォルトの選択はガウス関数です。以下で説明する他の関数も使用されます。
    • ガウス (デフォルト): これは鐘型の曲線です。ニューロンが更新される程度は、勝者ニューロンからの距離が増すにつれて滑らかに減少します。滑らかで連続的な遷移を提供し、データのトポロジーを保持します。安定して予測可能な動作のため、ほとんどの一般的な目的に適しています。
    • バブル: この機能は固定幅の近隣を作成します。この近隣内のすべてのニューロンは等しく更新され、近隣外のニューロンは更新されません（特定のデータポイントに対して）。計算コストが低く、実装が容易です。鋭い近隣境界が効果的なクラスタリングを妨げない小さなマップに役立ちます。
    • メキシカンハット: 中心に正の領域があり、その周りに負の領域があります。BMUに近いニューロンはデータポイントに近づくように更新され、遠くのニューロンはデータポイントから離れるように更新されます。この技術はコントラストを強化し、マップ内の特徴をシャープにします。明確なクラスタの分離を強調するため、クラスタを明確に分けることが望ましいパターン認識タスクにおいて効果的です。
    • 三角形: この機能は、BMUが最も大きな影響を持つ三角形として近傍のサイズを定義します。BMUからの距離に応じて線形に減少します。これは、画像、音声、または時系列データなど、クラスターや特徴間で徐々に遷移するデータのクラスタリングに使用されます。隣接するデータポイントは、類似の特性を共有することが期待されます。
  • 距離関数 (DISTANCE_FUNC): ニューロンとデータポイント間の距離を測定するために、4つの方法から選択できます：
    • ユークリッド距離（デフォルトの選択）：データが連続している場合に役立ち、直線距離を測定したいときに使用します。データポイントが均等に分布し、空間的に関連している場合、ほとんどの一般的なタスクに適しています。
    • コサイン距離：ベクトル間の角度が大きさよりも重要なテキストや高次元のスパースデータに適した選択です。データの方向性を比較するのに役立ちます。
    • マンハッタン距離：データポイントがグリッドや格子上（例：街区）にあるときに理想的です。これはユークリッド距離よりも外れ値に対して敏感ではありません。
    • チェビシェフ距離: 動きが任意の方向に発生する状況（例：チェスボード距離）に適しています。最大軸差を優先したい離散空間において便利です。
  • トポロジー (TOPOLOGY): グリッド内では、ニューロンは六角形または長方形の構造に配置できます：
    • 長方形（デフォルト）：各ニューロンは4つの隣接ニューロンを持ちます。データに明確な空間的関係がない場合に適した選択です。また、計算的にもシンプルです。
    • 六角形：各ニューロンは6つの隣接ニューロンを持ちます。データが六角形グリッドでより良く表現される空間的関係を持つ場合、これが推奨されるオプションです。これは円形または角度分布のデータに該当します。
  • トレーニング反復回数 (N_ITERATIONS): 原則として、トレーニング時間が長くなるほど、誤差が低くなり、重みが入力データとより良く整合します。しかし、モデルの性能は反復回数とともに漸近的に増加します。したがって、一定の反復回数を超えると、その後の相互作用からの性能向上はわずかになります。適切な反復回数を決定するには、いくつかの実験が必要です。このチュートリアルでは、モデルを5000回の反復でトレーニングします。

ハイパーパラメータの適切な設定を決定するために、データの小さなサブセットでさまざまなオプションを試すことをお勧めします。

結論

自己組織化マップは、教師なし学習のための強力なツールです。これらは、クラスタリング、次元削減、異常検知、およびデータ可視化に使用されます。高次元データの位相的特性を保持し、低次元グリッド上に表現するため、SOMは複雑なデータセットを視覚化し解釈するのを容易にします。

このチュートリアルでは、SOMの基本原則について説明し、MiniSom Pythonライブラリを使用してSOMを実装する方法を示しました。また、結果を視覚的に分析する方法をデモンストレーションし、SOMを訓練し、その性能を微調整するために使用される重要なハイパーパラメータについて説明しました。

Source:
https://www.datacamp.com/tutorial/self-organizing-maps