Mapas Autoorganizados: Una Guía Intuitiva con Ejemplos en Python

Configurando el Entorno para SOM

Antes de construir el SOM, necesitamos preparar el entorno con los paquetes necesarios.

Instalación de bibliotecas de Python

Necesitamos estos paquetes:

• MiniSom es una herramienta de Python basada en NumPy que crea y entrena SOMs.
• NumPy se utiliza para acceder a funciones matemáticas como dividir arreglos, obtener valores únicos, etc.
• matplotlib se utiliza para trazar varios gráficos y diagramas para visualizar los datos.
• El paquete datasets de sklearn se utiliza para importar conjuntos de datos sobre los que aplicar el SOM. 
• El paquete MinMaxScaler de sklearn normaliza el conjunto de datos. 

El siguiente fragmento de código importa estos paquetes: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Preparando el conjunto de datos

En este tutorial, usamos MiniSom para construir un SOM y luego entrenarlo en el conjunto de datos IRIS. Este dataset consiste en 3 clases de plantas de iris. Cada clase tiene 50 instancias. Para preparar los datos, seguimos estos pasos:

• Importar el conjunto de datos Iris desde sklearn,
• Extraer los vectores de datos y los escalares objetivo.
• Normaliza los vectores de datos. En este tutorial, utilizamos el MinMaxScaler de scikit-learn. 
• Declara un conjunto de etiquetas para cada una de las tres clases de plantas Iris. 

El siguiente código implementa estos pasos: 

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Implementación de Mapas Auto-Organizados (SOM) en Python

Para implementar un SOM en Python, definimos e inicializamos la cuadrícula antes de entrenarla en el conjunto de datos. Luego podemos visualizar las neuronas entrenadas y el conjunto de datos agrupado. 

Definiendo la cuadrícula SOM

Como se explicó anteriormente, un SOM es una cuadrícula de neuronas. Usando MiniSom, podemos crear cuadrículas de 2 dimensiones. Las dimensiones X e Y de la cuadrícula son el número de neuronas a lo largo de cada eje. Para definir la cuadrícula SOM, también necesitamos especificar:

• Las dimensiones X e Y de la cuadrícula
• El número de variables de entrada – este es el número de filas de datos.

Declara estos parámetros como constantes de Python:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

El código de muestra a continuación ilustra cómo declarar la cuadrícula usando MiniSom:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

Los primeros dos parámetros son el número de neuronas a lo largo de los ejes X e Y, y el tercer parámetro es el número de variables.

Declaramos otros parámetros e hiperpárametros al crear la cuadrícula SOM. Explicaremos estos más adelante en el tutorial. Por ahora, declara estos parámetros como se muestra a continuación:

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Crea un SOM usando estos parámetros:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Inicializando las neuronas

El comando anterior crea un SOM con pesos aleatorios para todas las neuronas. Inicializar las neuronas con pesos extraídos de los datos (en lugar de números aleatorios) puede hacer que el proceso de entrenamiento sea más eficiente.

Al usar MiniSom para crear un Mapa Auto-Organizado (SOM), hay dos formas de inicializar los pesos de las neuronas basándose en los datos:

• Inicialización aleatoria: Los pesos iniciales de las neuronas se extraen aleatoriamente de los datos de entrada. Hacemos esto aplicando la función .random_weights_init() al SOM. 
• Inicialización PCA: La inicialización mediante Análisis de Componentes Principales (PCA) utiliza los componentes principales de los datos de entrada para inicializar los pesos. Los pesos iniciales de las neuronas abarcan los primeros dos componentes principales. Esto a menudo conduce a una convergencia más rápida.

En esta guía, utilizamos la inicialización PCA. Para aplicar la inicialización PCA en los pesos del SOM, utiliza la .pca_weights_init() función como se muestra a continuación:

som.pca_weights_init(data)

Entrenando el SOM

El proceso de entrenamiento actualiza los pesos del SOM para minimizar la distancia entre las neuronas y los puntos de datos.

A continuación, explicamos el proceso de entrenamiento iterativo:

• Inicialización: Los vectores de peso de todas las neuronas se inicializan, típicamente con valores aleatorios. También es posible inicializar los pesos muestreando la distribución de datos de entrada.
• Selección de entrada: Se selecciona (aleatoriamente) un vector de entrada del conjunto de datos de entrenamiento.
• Identificación de BMU: Se identifica la neurona cuyo vector de peso es el más cercano al vector de entrada como la BMU.
• Actualización del vecindario: La BMU y sus neuronas vecinas actualizan sus vectores de peso. La tasa de aprendizaje y la función de vecindario deciden qué neuronas se actualizan y en qué medida. En el paso de iteración t, dado el vector de entrada x, el vector de peso de la neurona i es w_i, la tasa de aprendizaje (t), y la función de vecindario h_bi (esta función cuantifica la extensión de la actualización para la neurona i dado la neurona BMU b), la fórmula de actualización de peso para la neurona i se expresa como:
• Tasa de decaimiento de la tasa de aprendizaje y el radio de vecindario: Tanto la tasa de aprendizaje como el radio de vecindario disminuyen con el tiempo. En las primeras iteraciones, el proceso de entrenamiento realiza ajustes más grandes sobre un vecindario más amplio. Las iteraciones posteriores ayudan a afinar los pesos realizando cambios más pequeños en los pesos de las neuronas adyacentes. Esto permite que el mapa se estabilice y converja. 

Para entrenar el SOM, presentamos al modelo los datos de entrada. Podemos elegir entre uno de dos enfoques para hacerlo: 

• Seleccionar muestras al azar de los datos de entrada. La .train_random() función implementa esta técnica. 
• Ejecutar secuencialmente los vectores en los datos de entrada. Esto se hace utilizando la función .train_batch() función.

Estas funciones aceptan los datos de entrada y el número de iteraciones como parámetros. En esta guía, utilizamos la función .train_random() función. Declara el número de iteraciones como una constante y pásalo a la función de entrenamiento:

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

Después de ejecutar el script y completar el entrenamiento, se muestra un mensaje con el error de cuantización:

quantization error: 0.05357240680504421 

El error de cuantización indica la cantidad de información perdida cuando el SOM cuantiza (reduce la dimensionalidad de) los datos. Un gran error de cuantización indica una mayor distancia entre las neuronas y los puntos de datos. También significa que el agrupamiento es menos confiable.

Visualizando neuronas SOM

Ahora tenemos un modelo SOM entrenado. Para visualizarlo, usamos un mapa de distancias (también conocido como un U-matriz). El mapa de distancias muestra las neuronas del SOM como una cuadrícula de celdas. El color de cada celda representa su distancia a las neuronas vecinas.

El mapa de distancias es una cuadrícula con las mismas dimensiones que el SOM. Cada celda en el mapa de distancias es la suma normalizada de las distancias (euclidianas) entre una neurona y sus vecinas.

Accede al mapa de distancias SOM utilizando la función .distance_map(). Para generar la U-matriz, seguimos estos pasos:

• Usa pyplot para crear una figura con las mismas dimensiones que el SOM. En este ejemplo, las dimensiones son 8×8. 
• Dibuja el mapa de distancias utilizando matplotlib con la función .pcolor() En este ejemplo, usamos gist_yarg como esquema de color.
• Muestra la barra de colores, un mapeo de índices que asigna diferentes colores a diferentes valores escalares. En este caso, dado que las distancias están normalizadas, los valores escalares de distancia van de 0 a 1.

El código a continuación implementa estos pasos:

# crear la cuadrícula
plt.figure(figsize=(8, 8))
# trazar el mapa de distancia
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# mostrar la barra de colores
plt.colorbar()
plt.show()

En este ejemplo, la U-matriz utiliza un esquema de colores monotono. Se puede entender siguiendo estas pautas:

• Los tonos más claros representan neuronas cercanas entre sí, y los tonos más oscuros representan neuronas más alejadas de otras.
• Grupos de tonos más claros pueden interpretarse como clústeres. Los nodos oscuros entre los clústeres pueden interpretarse como los límites entre clústeres.

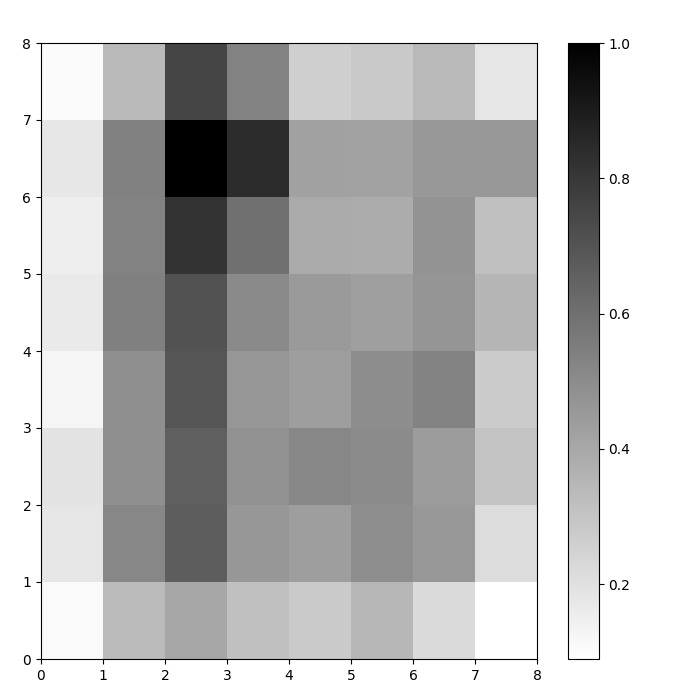
Figura 1: U-matriz de SOM entrenada con el conjunto de datos Iris (imagen del autor)

Evaluando los Resultados de Clustering de SOM

La figura anterior ilustró gráficamente las neuronas del SOM. En esta sección, mostramos cómo visualizar cómo el SOM agrupó los datos.

Identificando clústeres

Superponemos marcadores sobre la U-matriz anterior para denotar a qué clase de planta Iris representa cada celda (neurona). Para hacer esto:

• Como antes, crea una figura de 8×8 usando pyplot, traza el mapa de distancias y muestra la barra de color. 
• Especifica un array de tres marcadores de matplotlib, uno para cada clase de planta Iris. 
• Especifica un array de tres códigos de color de matplotlib, uno para cada clase de planta Iris. 
• Traza de manera iterativa el neurona ganadora para cada punto de datos:
• Determina las (coordenadas del) neurona ganadora para cada punto de datos usando la .winner() función. 
• Plotea la posición de cada neurona ganadora en el medio de cada celda en la cuadrícula. w[0] y w[1] dan las coordenadas X e Y de la neurona, respectivamente. Se agrega un valor de 0.5 a cada coordenada para ploteada en el medio de la celda. 

El código a continuación muestra cómo hacer esto:

# plotea el mapa de distancias
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# crea los marcadores y colores para cada clase
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# plotea la neurona ganadora para cada punto de datos
for count, datapoint in enumerate(data):
    # obtiene la ganadora
    w = som.winner(datapoint)  
    # coloca un marcador en la posición ganadora para el punto de datos de muestra
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

La imagen resultante se muestra a continuación:

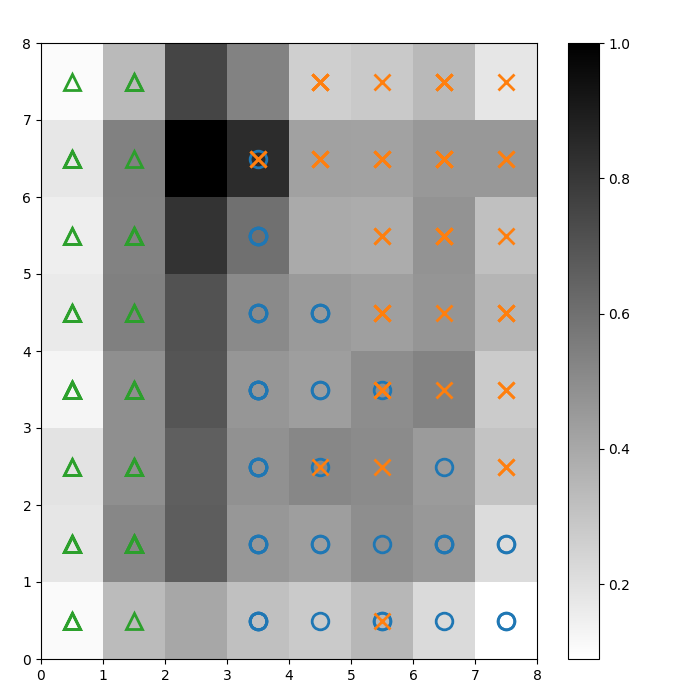
Figura 2: U-matriz superpuesta con marcadores de clase (imagen del autor)

Basado en la documentación del conjunto de datos Iris, “una clase es linealmente separable de las otras 2; las últimas no son linealmente separables entre sí”. En la U-matriz anterior, estas tres clases están representadas por tres marcadores: triángulo, círculo y cruz.

Nota que no hay un límite claro entre los círculos azules y las cruces naranjas. Además, dos clases están superpuestas en la misma neurona en muchas celdas. Esto significa que la neurona está a la misma distancia de ambas clases.

Visualizando el resultado del agrupamiento

Un SOM es un modelo de agrupamiento. Los puntos de datos similares se mapean al mismo neurona. Los puntos de datos de la misma clase se mapean a un clúster de neuronas vecinas. Graficamos todos los puntos de datos en la cuadrícula del SOM para estudiar mejor el comportamiento de agrupamiento.

Los siguientes pasos describen cómo crear este diagrama de dispersión:

• Obtén las coordenadas X e Y de la neurona ganadora para cada punto de datos.
• Grafica el mapa de distancias, como hicimos para la Figura 1.
• Utiliza plt.scatter() para hacer un diagrama de dispersión de todas las neuronas ganadoras para cada punto de datos. Añade un desplazamiento aleatorio a cada punto para evitar superposiciones entre los puntos de datos dentro de la misma celda.

Implementamos estos pasos en el código a continuación: 

# obtener las coordenadas X e Y de la neurona ganadora para cada punto de datosw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# trazar el mapa de distancias
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# hacer un diagrama de dispersión de todas las neuronas ganadoras para cada punto de datos
# añadir un desplazamiento aleatorio a cada punto para evitar superposiciones
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

El siguiente gráfico muestra el diagrama de dispersión resultante:

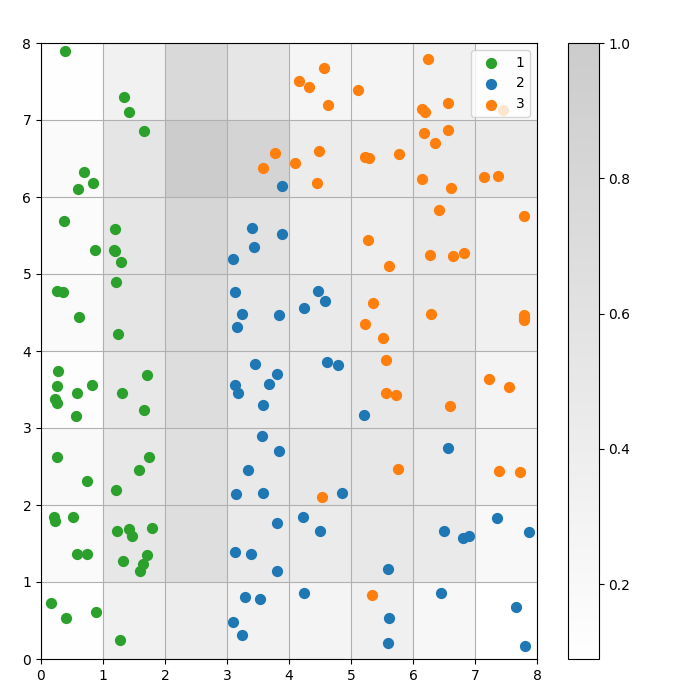Figura 3: Gráfico de dispersión de puntos de datos dentro de las celdas (imagen del autor)

En el gráfico de dispersión anterior, observa que:

• Algunas celdas contienen tanto puntos azules como naranjas.
• Los puntos verdes están claramente separados del resto de los datos, pero los puntos azules y naranjas no están separados de manera limpia.
• Las observaciones anteriores coinciden con el hecho de que solo uno de los tres grupos en el conjunto de datos de Iris tiene un límite claro.
• En Figura 1, los nodos oscuros entre los grupos (que pueden interpretarse como los límites entre grupos) coinciden con celdas vacías en el gráfico de dispersión.

Puedes acceder y ejecutar el código completo en este cuaderno de DataLab.

Ajuste del Modelo SOM

Las secciones anteriores mostraron cómo crear y entrenar un modelo SOM y cómo estudiar los resultados visualmente. En esta sección, discutimos cómo ajustar el rendimiento de los modelos SOM.

Parámetros hiperimportantes a ajustar

Al igual que con cualquier modelo de aprendizaje automático, los hiperparámetros impactan considerablemente en el rendimiento del modelo.

Algunos de los hiperparámetros importantes en el entrenamiento de SOMs son:

• El tamaño de la cuadrícula decide el tamaño del mapa. El número de neuronas en un mapa con un tamaño de cuadrícula de AxB es A*B.
• La tasa de aprendizaje decide cuánto se cambian los pesos en cada iteración. Establecemos la tasa de aprendizaje inicial, y esta disminuye con el tiempo según la función de decaimiento.
• La función de decaimiento decide el grado en que se disminuye la tasa de aprendizaje en cada iteración subsiguiente.
• La función de vecindario es una función matemática que especifica qué neuronas se consideran como los vecinos del BMU.
• La desviación estándar especifica la extensión de la función de vecindario. Por ejemplo, una función de vecindario gaussiana con una alta desviación estándar tendrá un vecindario más grande que la misma función con una desviación estándar más pequeña. Establecemos la desviación estándar inicial, que disminuye con el tiempo de acuerdo con la función de decaimiento sigma.
• La función de decaimiento sigma controla cuánto se reduce la desviación estándar en cada iteración subsiguiente.
• El número de iteraciones de entrenamiento decide cuántas veces se actualizan los pesos. En cada iteración de entrenamiento, los pesos de las neuronas se actualizan una vez.
• La función de distancia es una función matemática que calcula la distancia entre neuronas y puntos de datos. 
• La topología decide la disposición de la estructura de la cuadrícula. Las neuronas en la cuadrícula pueden disponerse en un patrón rectangular o hexagonal. 

En la siguiente sección, discutimos pautas para establecer los valores de estos hiperparámetros. 

Impacto de la sintonización de hiperparámetros

Los valores de los hiperparámetros deben decidirse en función del modelo y del conjunto de datos. Hasta cierto punto, determinar estos valores es un proceso de prueba y error. En esta sección, ofrecemos pautas para ajustar cada hiperparámetro. Junto a cada hiperparámetro, mencionamos (entre paréntesis) las constantes de Python respectivas utilizadas en el código de ejemplo.

• Tamaño de la cuadrícula (SOM_X_AXIS_NODES y SOM_X_AXIS_NODES): El tamaño de la cuadrícula depende del tamaño del conjunto de datos. La regla general es que dado un conjunto de datos de tamaño N, la cuadrícula debe contener aproximadamente 5*sqrt(N) neuronas. Por ejemplo, si el conjunto de datos tiene 150 muestras, la cuadrícula debe contener 5*sqrt(150) = aproximadamente 61 neuronas. En este tutorial, el conjunto de datos Iris tiene 150 filas y utilizamos una cuadrícula de 8×8.
• Tasa de aprendizaje inicial (ALPHA): Una tasa más alta acelera la convergencia, mientras que tasas más bajas se utilizan para ajustes más finos después de las iteraciones iniciales. La tasa de aprendizaje inicial debe ser lo suficientemente grande como para permitir una rápida adaptación, pero no tan grande que exceda los valores óptimos de peso. En este artículo, la tasa de aprendizaje inicial es 0.5. 
• Desviación estándar inicial (SIGMA0): Determina el tamaño o la dispersión inicial del vecindario. Un valor más grande considera patrones más globales. En este ejemplo, usamos una desviación estándar inicial de 1.5. 
• Para la tasa de descomposición (DECAY_FUNC) y la tasa de descomposición sigma (SIGMA_DECAY_FUNC), podemos elegir entre uno de tres tipos de funciones de descomposición: 
• Decaimiento inverso: Esta función es adecuada si los datos tienen patrones globales y locales. En tales casos, necesitamos una fase más larga de aprendizaje amplio antes de centrarnos en los patrones locales. 
• Decaimiento lineal: Esto es bueno para conjuntos de datos donde queremos un tamaño de vecindario constante y uniforme o una reducción en la tasa de aprendizaje. Esto es útil si los datos no necesitan mucho ajuste fino.
• Decaimiento asintótico: Esta función es útil si los datos son complejos y de alta dimensión. En tales casos, es mejor dedicar más tiempo a la exploración global antes de pasar gradualmente a detalles más finos. 
• Función de vecindad (NEIGHBORHOOD_FUNC): La elección predeterminada de la función de vecindad es la función gaussiana. Otras funciones, como se explica a continuación, también se utilizan.
• Gaussiana (predeterminada): Esta es una curva en forma de campana. La medida en que se actualiza una neurona disminuye suavemente a medida que aumenta su distancia desde la neurona ganadora. Proporciona una transición suave y continua y preserva la topología de los datos. Es adecuada para la mayoría de los propósitos generales debido a su comportamiento estable y predecible.
• Burbuja: Esta función crea un vecindario de ancho fijo. Todas las neuronas dentro de este vecindario se actualizan por igual, y las neuronas fuera de este vecindario no se actualizan (para un punto de datos dado). Es computacionalmente más barato y más fácil de implementar. Es útil para mapas más pequeños donde los límites del vecindario definidos no comprometen el agrupamiento efectivo.
• Sombrero mexicano: Tiene una región central positiva rodeada por una región negativa. Las neuronas cercanas a la BMU se actualizan para acercarse al punto de datos, y las neuronas más alejadas se actualizan para alejarse del punto de datos. Esta técnica mejora el contraste y agudiza las características en el mapa. Dado que enfatiza los clústeres distintos, es efectiva en tareas de reconocimiento de patrones donde se desea una clara separación de clústeres.
• Triángulo: Esta función define el tamaño del vecindario como un triángulo, donde el BMU tiene la mayor influencia. Disminuye linealmente con la distancia desde el BMU. Se utiliza para agrupar datos con transiciones graduales entre clústeres o características, como datos de imagen, habla o series temporales, donde se espera que los puntos de datos vecinos compartan características similares.
• Función de distancia (DISTANCE_FUNC): Para medir la distancia entre neuronas y puntos de datos, podemos elegir entre 4 métodos:
• Distancia euclidiana (opción predeterminada): Útil cuando los datos son continuos y queremos medir la distancia en línea recta. Se adapta a la mayoría de las tareas generales, especialmente cuando los puntos de datos están distribuidos uniformemente y son espacialmente relacionados.
• Distancia coseno: Buen opción para datos de texto o de alta dimensión y dispersos donde el ángulo entre los vectores es más importante que la magnitud. Es útil para comparar la direccionalidad en los datos.
• Distancia de Manhattan: Ideal cuando los puntos de datos están en una cuadrícula o red (por ejemplo, bloques de la ciudad). Esto es menos sensible a los valores atípicos que la distancia euclidiana.
• Distancia de Chebyshev: Adecuada para situaciones donde el movimiento puede ocurrir en cualquier dirección (por ejemplo, distancias en un tablero de ajedrez). Es útil para espacios discretos donde queremos priorizar la diferencia máxima en el eje.
• Topología (TOPOLOGY): En una cuadrícula, las neuronas pueden estar dispuestas en una estructura hexagonal o rectangular: 
• Rectangular (predeterminado): cada neurona tiene 4 vecinos inmediatos. Esta es la opción correcta cuando los datos no tienen una relación espacial clara. También es computacionalmente más simple.
• Hexagonal: cada neurona tiene 6 vecinos. Esta es la opción preferida si los datos tienen relaciones espaciales que se representan mejor con una cuadrícula hexagonal. Este es el caso de distribuciones de datos circulares o angulares.
• Número de iteraciones de entrenamiento (N_ITERACIONES): En principio, tiempos de entrenamiento más largos conducen a errores más bajos y una mejor alineación de los pesos con los datos de entrada. Sin embargo, el rendimiento del modelo aumenta asintóticamente con el número de iteraciones. Por lo tanto, después de un cierto número de iteraciones, el aumento de rendimiento de las interacciones subsiguientes es solo marginal. Decidir el número correcto de iteraciones requiere algo de experimentación. En este tutorial, entrenamos el modelo durante 5000 iteraciones. 

Para determinar la configuración adecuada de hiperparámetros, recomendamos experimentar con varias opciones en un subconjunto más pequeño de los datos.

Conclusión

Los mapas autoorganizados son una herramienta robusta para aprendizaje no supervisado. Se utilizan para la agrupación, reducción de dimensionalidad, detección de anomalías y visualización de datos. Dado que preservan las propiedades topológicas de datos de alta dimensión y los representan en una cuadrícula de menor dimensión, los SOMs facilitan la visualización e interpretación de conjuntos de datos complejos.

Este tutorial discutió los principios subyacentes de los SOMs y mostró cómo implementar un SOM utilizando la biblioteca MiniSom de Python. También demostró cómo analizar visualmente los resultados y explicó los importantes hiperparámetros utilizados para entrenar los SOMs y ajustar su rendimiento.