خرائط التنظيم الذاتي: دليل بديهي مع أمثلة بلغة بايثون

إعداد البيئة لشبكات الخرائط الذاتية (SOM)

قبل بناء SOM، نحتاج إلى إعداد البيئة بالحزم الضرورية. 

تثبيت مكتبات بايثون 

نحتاج هذه الحزم: 

• MiniSom هي أداة بايثون تعتمد على NumPy لإنشاء وتدريب SOMs. 
• يتم استخدام NumPy للوصول إلى الدوال الرياضية مثل تقسيم المصفوفات، والحصول على القيم الفريدة، وغيرها. 
• matplotlib تُستخدم لرسم الرسوم البيانية والمخططات المختلفة لتصور البيانات. 
• حزمة datasets من sklearn تُستخدم لاستيراد مجموعات البيانات التي سيتم تطبيق SOM عليها. 
• حزمة MinMaxScaler من sklearn تقوم بتطبيع مجموعة البيانات. 

الكود التالي يستورد هذه الحزم: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

تحضير مجموعة البيانات

في هذا البرنامج التعليمي، نستخدم MiniSom لبناء SOM ثم نقوم بتدريبه على مجموعة بيانات IRIS القياسية. تتكون هذه المجموعة من 3 فئات من نباتات السوسن. تحتوي كل فئة على 50 حالة. لتحضير البيانات، نتبع هذه الخطوات: 

• استيراد مجموعة بيانات السوسن من sklearn، 
• استخراج متجهات البيانات والقياسات المستهدفة. 
• تطبيع متجهات البيانات. في هذا البرنامج التعليمي، نستخدم MinMaxScaler من scikit-learn.
• قم بإعلان مجموعة من التسميات لكل من الفئات الثلاث لنباتات إيريس.

الكود التالي ينفذ هذه الخطوات:

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

تنفيذ خرائط التنظيم الذاتي (SOM) في بايثون

لتنفيذ SOM في بايثون، نقوم بتعريف الشبكة وتهيئتها قبل تدريبها على مجموعة البيانات. يمكننا بعد ذلك تصور الخلايا العصبية المدربة ومجموعة البيانات المجمعة.

تعريف شبكة SOM

كما تم الشرح سابقًا، فإن SOM هو شبكة من الخلايا العصبية. باستخدام MiniSom، يمكننا إنشاء شبكات ثنائية الأبعاد. أبعاد الشبكة على المحورين X و Y هي عدد الخلايا العصبية على كل محور. لتعريف شبكة SOM، نحتاج أيضًا إلى تحديد:

• أبعاد X و Y للشبكة
• عدد المتغيرات المدخلة – هذا هو عدد صفوف البيانات.

قم بإعلان هذه المعلمات كثوابت في بايثون:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

يوضح الكود النموذجي أدناه كيفية إعلان الشبكة باستخدام MiniSom:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

المعلمين الأولين هما عدد الخلايا العصبية على المحورين X و Y، والمعلمة الثالثة هي عدد المتغيرات.

نعلن عن معلمات أخرى والمعلمات الفائقة أثناء إنشاء شبكة SOM. سنشرح هذه لاحقًا في البرنامج التعليمي. في الوقت الحالي، أعلن عن هذه المعلمات كما هو موضح أدناه:

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

قم بإنشاء SOM باستخدام هذه المعلمات:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

تهيئة الخلايا العصبية

الأمر أعلاه ينشئ SOM بأوزان عشوائية لجميع الخلايا العصبية. يمكن أن تجعل تهيئة الخلايا العصبية بأوزان مستمدة من البيانات (بدلاً من أرقام عشوائية) عملية التدريب أكثر كفاءة.

عند استخدام MiniSom لإنشاء خريطة ذاتية التنظيم (SOM)، هناك طريقتان لتهيئة أوزان الخلايا العصبية استنادًا إلى البيانات:

• تهيئة عشوائية: يتم سحب الأوزان الأولية للخلايا العصبية عشوائيًا من بيانات الإدخال. نقوم بذلك عن طريق تطبيق دالة .random_weights_init() على الـ SOM.
• تهيئة PCA: تستخدم تهيئة تحليل المكونات الرئيسية (PCA) المكونات الرئيسية الرئيسية لبيانات الإدخال لتهيئة الأوزان. تمتد الأوزان الأولية للخلايا العصبية عبر أول مكونين رئيسيين. وغالبًا ما يؤدي ذلك إلى تقارب أسرع.

في هذا الدليل، نستخدم تهيئة PCA. لتطبيق تهيئة PCA على أوزان SOM، استخدم .pca_weights_init() الدالة كما هو موضح أدناه:

som.pca_weights_init(data)

تدريب SOM

تعمل عملية التدريب على تحديث أوزان SOM لتقليل المسافة بين الخلايا العصبية ونقاط البيانات.

فيما يلي، نشرح عملية التدريب التكرارية:

• التهيئة: يتم تهيئة متجهات الوزن لجميع الخلايا العصبية، عادةً بقيم عشوائية. من الممكن أيضًا تهيئة الأوزان من خلال أخذ عينات من توزيع بيانات الإدخال.
• اختيار الإدخال: يتم اختيار متجه الإدخال (بشكل عشوائي) من مجموعة بيانات التدريب.
• تحديد BMU: يتم تحديد الخلية العصبية التي تمتلك متجه الوزن الأقرب لمتجه الإدخال كـ BMU.
• تحديث الجوار: تقوم وحدة المراسلة الأفضل (BMU) والخلايا العصبية المجاورة لها بتحديث متجهات الوزن الخاصة بها. تحدد معدل التعلم ودالة الجوار الخلايا العصبية التي يتم تحديثها ومقدار هذا التحديث. في خطوة التكرار t، بالنظر إلى متجه الإدخال x، متجه الوزن للخلايا العصبية i هو w_i، معدل التعلم (t)، ودالة الجوار h_bi (تقوم هذه الدالة بتحديد مدى التحديث للخلايا العصبية i بالنظر إلى خلايا BMU العصبية b)، يتم التعبير عن صيغة تحديث الوزن للخلايا العصبية i كالتالي:
• معدل تدهور معدل التعلم ونطاق الجوار: كل من معدل التعلم ونطاق الجوار يتناقصان مع مرور الوقت. في التكرارات المبكرة، يقوم عملية التدريب بإجراء تعديلات أكبر على نطاق أوسع. تساعد التكرارات اللاحقة في تحسين الأوزان من خلال إجراء تغييرات أصغر على أوزان الخلايا العصبية المجاورة. وهذا يسمح للخريطة بالاستقرار والتقارب. 

لتدريب SOM، نقدم النموذج مع بيانات الإدخال. يمكننا الاختيار من بين نهجين للقيام بذلك: 

• اختيار عينات عشوائية من بيانات الإدخال. تقوم وظيفة .train_random() بتنفيذ هذه التقنية. 
• قم بتشغيل المتجهات في بيانات الإدخال بشكل متسلسل. يتم ذلك باستخدام .train_batch() الدالة.

تقبل هذه الدوال بيانات الإدخال وعدد التكرارات كمعلمات. في هذا الدليل، نستخدم .train_random() الدالة. قم بتعريف عدد التكرارات كثابت ومرره إلى دالة التدريب:

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

بعد تنفيذ البرنامج النصي وإكمال التدريب، يتم عرض رسالة تحتوي على خطأ التكميم:

quantization error: 0.05357240680504421 

تشير خطأ الكوانتيزاسيون إلى مقدار المعلومات المفقودة عندما يقوم SOM بتكميم (تقليل أبعاد) البيانات. تشير خطأ الكوانتيزاسيون الكبير إلى وجود مسافة أكبر بين الخلايا العصبية ونقاط البيانات. كما يعني أن التجميع أقل موثوقية.

تصوير خلايا SOM العصبية

لدينا الآن نموذج SOM مدرب. لتصويره، نستخدم خريطة المسافة (المعروفة أيضًا باسم مصفوفة U). تعرض خريطة المسافة خلايا SOM العصبية كشبكة من الخلايا. يمثل لون كل خلية المسافة من الخلايا العصبية المجاورة.

خريطة المسافة هي شبكة بنفس أبعاد SOM. كل خلية في خريطة المسافة هي المجموع الطبيعي (الإقليدي) للمسافات بين خلية عصبية وجيرانها.

الوصول إلى خريطة المسافة SOM باستخدام دالة .distance_map(). لإنشاء مصفوفة U، نتبع هذه الخطوات:

• استخدم pyplot لإنشاء شكل بنفس أبعاد SOM. في هذا المثال، الأبعاد هي 8×8.
• قم برسم خريطة المسافة باستخدام matplotlib باستخدام دالة .pcolor() في هذا المثال، نستخدم gist_yarg كخطة ألوان.
• عرض colorbar، وهو فهرس يربط ألوانًا مختلفة بقيم عددية مختلفة. في هذه الحالة، بما أن المسافات تم تطبيعها، تتراوح القيم العددية للمسافة من 0 إلى 1. 

الكود أدناه ينفذ هذه الخطوات: 

# إنشاء الشبكة
plt.figure(figsize=(8, 8))
# رسم خريطة المسافة
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# عرض شريط الألوان
plt.colorbar()
plt.show()

في هذا المثال، تستخدم مصفوفة U نظام ألوان متدرج. يمكن فهمه باستخدام هذه الإرشادات:

• تُمثل الظلال الفاتحة الخلايا العصبية المتقاربة، بينما تمثل الظلال الداكنة الخلايا العصبية البعيدة عن بعضها البعض. 
• يمكن تفسير مجموعات الظلال الفاتحة على أنها مجموعات. يمكن تفسير العقد الداكنة بين المجموعات على أنها الحدود بين المجموعات.

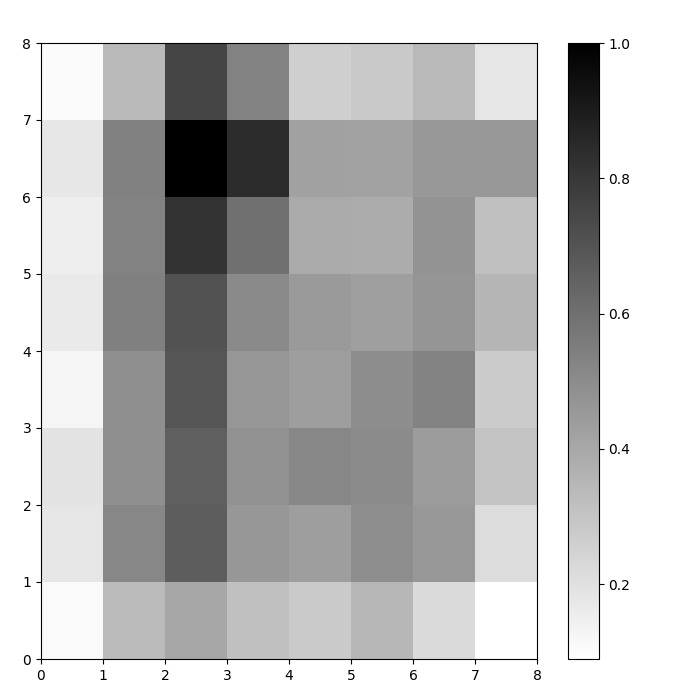
الشكل 1: مصفوفة U لـ SOM المدربة على مجموعة بيانات إيريس (صورة من المؤلف)

تقييم نتائج تجميع SOM

عرض الشكل السابق بيانيًا خلايا عصبية SOM. في هذا القسم، نوضح كيفية تصور كيفية تجميع SOM للبيانات.

تحديد المجموعات

نقوم بتراكب علامات فوق مصفوفة U أعلاه للإشارة إلى أي فئة من نبات إيريس تمثلها كل خلية (عصبون). للقيام بذلك:

• كما كان من قبل، قم بإنشاء شكل 8×8 باستخدام pyplot، ارسم خريطة المسافات، وعرض شريط الألوان. 
• حدد مصفوفة من ثلاثة أشكال matplotlib، واحد لكل فئة من نباتات Iris. 
• حدد مصفوفة من ثلاثة رموز ألوان matplotlib، واحد لكل فئة من نباتات Iris. 
• قم برسم العصبون الفائز لكل نقطة بيانات بشكل تكراري:
• حدد (إحداثيات) الخلية الفائزة لكل نقطة بيانات باستخدام دالة .winner() .
• قم برسم موقع كل خلية فائزة في منتصف كل خلية على الشبكة. w[0] و w[1] تعطي إحداثيات الخلية على المحورين X و Y، على التوالي. يتم إضافة قيمة 0.5 إلى كل إحداثي لرسمه في منتصف الخلية.

الكود أدناه يوضح كيفية القيام بذلك:

# رسم خريطة المسافة
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# إنشاء العلامات والألوان لكل فئة
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# رسم الخلية الفائزة لكل نقطة بيانات
for count, datapoint in enumerate(data):
    # الحصول على الفائز
    w = som.winner(datapoint)  
    # وضع علامة على الموقع الفائز لنقطة البيانات العينة
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

تظهر الصورة الناتجة أدناه: 

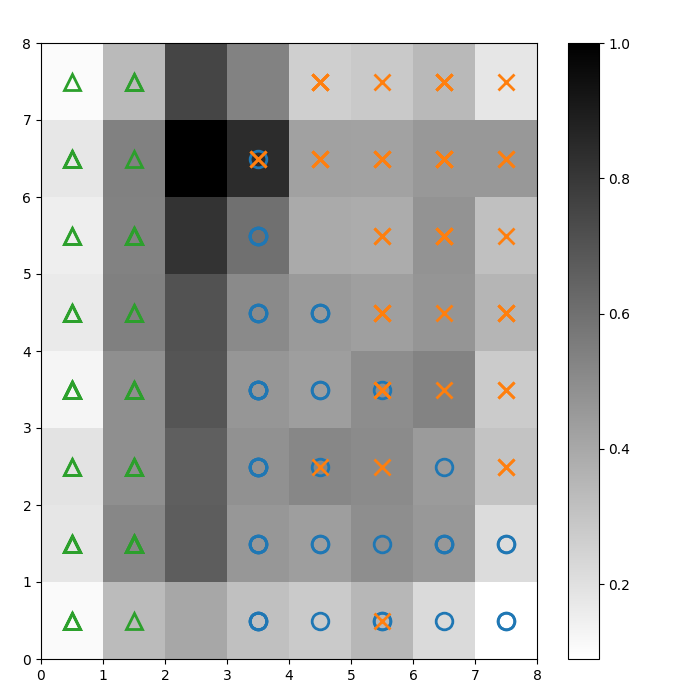
الشكل 2: مصفوفة U مغطاة بعلامات الفئات (صورة من تأليف الكاتب)

استنادًا إلى وثائق مجموعة بيانات إيريس، “فئة واحدة فصلها خطيًا عن الفئتين الأخريين؛ الأخيرة ليست مفصولة خطيًا عن بعضها البعض”. في مصفوفة U أعلاه، تمثل هذه الفئات الثلاث من خلال ثلاث علامات – مثلث، دائرة، وعلامة زائد. 

لاحظ أنه لا يوجد حد واضح بين الدوائر الزرقاء وعلامات الزائد البرتقالية. علاوة على ذلك، يتم تراكب فئتين على نفس الخلايا العصبية في العديد من الخلايا. وهذا يعني أن الخلية العصبية تبعد مسافة متساوية عن الفئتين. 

تصوير نتيجة التجميع

نموذج SOM هو نموذج تجميع. النقاط البيانية المماثلة تتطابق مع نفس الخلية العصبية. نقاط البيانات من نفس الفئة تتطابق مع مجموعة من الخلايا العصبية المجاورة. نقوم برسم جميع النقاط البيانية على شبكة SOM لدراسة سلوك التجميع بشكل أفضل.

تصف الخطوات التالية كيفية إنشاء هذا الرسم البياني المتناثر:

• احصل على إحداثيات X و Y للخلية العصبية الفائزة لكل نقطة بيانات.
• ارسم خريطة المسافة، كما فعلنا من أجل الشكل 1.
• استخدم plt.scatter() لإنشاء مخطط مبعثر لجميع الخلايا العصبية الفائزة لكل نقطة بيانات. أضف انحرافًا عشوائيًا لكل نقطة لتجنب التداخل بين نقاط البيانات داخل نفس الخلية.

نقوم بتنفيذ هذه الخطوات في الكود أدناه: 

# احصل على إحداثيات X و Y للخلايا العصبية الفائزة لكل نقطة بياناتw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# رسم خريطة المسافة
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# قم بعمل مخطط مبعثر لجميع الخلايا العصبية الفائزة لكل نقطة بيانات
# أضف انحرافًا عشوائيًا لكل نقطة لتجنب التداخل
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

يوضح الرسم البياني التالي مخطط التشتت الناتج:

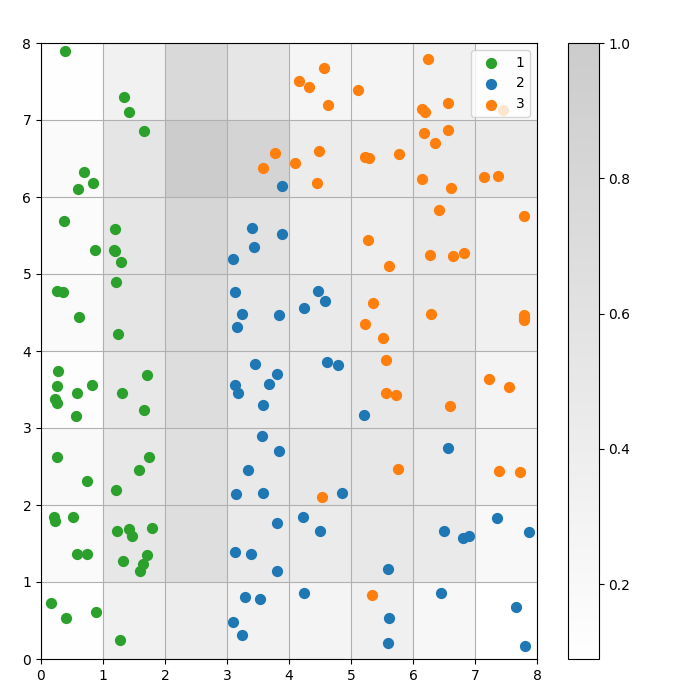الشكل 3: رسم بياني مبعثر لنقاط البيانات داخل الخلايا (صورة من المؤلف)

في الرسم البياني المبعثر أعلاه، لاحظ أن: 

• بعض الخلايا تحتوي على نقاط زرقاء وبرتقالية. 
• النقاط الخضراء مفصولة بوضوح عن بقية البيانات، لكن النقاط الزرقاء والبرتقالية ليست مفصولة بشكل نظيف. 
• تتوافق الملاحظات السابقة مع حقيقة أن واحدة فقط من الثلاث مجموعات في مجموعة بيانات إيريس لها حدود واضحة.
• في الشكل 1، تتطابق العقد الداكنة بين المجموعات (والتي يمكن تفسيرها على أنها الحدود بين المجموعات) مع الخلايا الفارغة في مخطط التشتت.

يمكنك الوصول إلى وتشغيل الكود الكامل على هذا الدفتر في DataLab.

ضبط نموذج SOM

أظهرت الأقسام السابقة كيفية إنشاء وتدريب نموذج SOM وكيفية دراسة النتائج بصريًا. في هذا القسم، نناقش كيفية ضبط أداء نماذج SOM.

المعلمات الفائقة الرئيسية لضبطها

كما هو الحال مع أي نموذج تعلم آلي، تؤثر المعلمات الفائقة بشكل كبير على أداء النموذج.

بعض المعلمات الفائقة المهمة في تدريب SOMs هي:

• يحدد حجم الشبكة حجم الخريطة. عدد الخلايا العصبية في خريطة بحجم شبكة AxB هو A*B.
• معدل التعلم يحدد مقدار تغيير الأوزان في كل تكرار. نقوم بتحديد معدل التعلم الابتدائي، وينخفض مع مرور الوقت وفقًا لدالة الانخفاض. 
• دالة الانخفاض تحدد مدى انخفاض معدل التعلم في كل تكرار لاحق. 
• الدالة الجوار هي دالة رياضية تحدد أي الخلايا العصبية يجب اعتبارها جيران الـ BMU. 
• تحدد الانحراف المعياري انتشار دالة الجوار. على سبيل المثال، ستحتوي دالة الجوار الجاوسية ذات الانحراف المعياري العالي على جوار أكبر من نفس الدالة ذات الانحراف المعياري المنخفض. نحن نحدد الانحراف المعياري الأولي، الذي ينقص مع مرور الوقت وفقًا لدالة تدهور سيغما. 
• وظيفة انحلال سيغما تتحكم في مقدار تقليل الانحراف المعياري في كل تكرار لاحق. 
• عدد تكرارات التدريب يحدد عدد المرات التي يتم فيها تحديث الأوزان. في كل تكرار تدريب، يتم تحديث أوزان الخلايا العصبية مرة واحدة. 
• وظيفة المسافة هي دالة رياضية تحسب المسافة بين الخلايا العصبية ونقاط البيانات. 
• تحدد التوبولوجيا تصميم هيكل الشبكة. يمكن ترتيب الخلايا العصبية في الشبكة في نمط مستطيل أو سداسي. 

في القسم التالي، نناقش الإرشادات لتحديد قيم هذه المعلمات الفائقة. 

أثر ضبط المعلمات الفائقة

يجب تحديد قيم المعاملات الفائقة بناءً على النموذج ومجموعة البيانات. إلى حد ما، فإن تحديد هذه القيم هو عملية تجريبية. في هذا القسم، نقدم إرشادات لضبط كل معامل فائق. بجانب كل معامل فائق، نذكر (بين قوسين) الثوابت الخاصة بلغة بايثون المستخدمة في الكود النموذجي.

• حجم الشبكة (SOM_X_AXIS_NODES و SOM_X_AXIS_NODES): يعتمد حجم الشبكة على حجم مجموعة البيانات. القاعدة العامة هي أنه بالنظر إلى مجموعة بيانات بحجم N، يجب أن تحتوي الشبكة على حوالي 5*sqrt(N) خلايا عصبية. على سبيل المثال، إذا كانت مجموعة البيانات تحتوي على 150 عينة، يجب أن تحتوي الشبكة على 5*sqrt(150) = حوالي 61 خلية عصبية. في هذا الدرس، تحتوي مجموعة بيانات إيريس على 150 صفاً ونستخدم شبكة بحجم 8×8. 
• معدل التعلم الأولي(ALPHA): معدل أعلى يسرع من التقارب، بينما تُستخدم المعدلات المنخفضة للتعديلات الدقيقة بعد التكرارات المبكرة. يجب أن يكون معدل التعلم الأولي كبيرًا بما يكفي لتمكين التكيف السريع ولكن ليس كبيرًا لدرجة أنه يتجاوز القيم المثلى للأوزان. في هذه المقالة، معدل التعلم الأولي هو 0.5.
• الانحراف المعياري الأولي(SIGMA0): يحدد الحجم الأولي أو الانتشار للجوار. قيمة أكبر تأخذ في الاعتبار المزيد من الأنماط العالمية. في هذا المثال، نستخدم انحرافًا معياريًا ابتدائيًا قدره 1.5.
• بالنسبة لـ معدل التدهور (DECAY_FUNC) ومعدل تدهور سيغما (SIGMA_DECAY_FUNC)، يمكننا الاختيار من بين ثلاثة أنواع من دوال التدهور:
• الانخفاض العكسي: هذه الدالة مناسبة إذا كانت البيانات تحتوي على أنماط عالمية ومحلية. في مثل هذه الحالات، نحتاج إلى مرحلة أطول من التعلم الواسع قبل التركيز على الأنماط المحلية.
• الانخفاض الخطي: هذا جيد لمجموعات البيانات حيث نريد حجم جيرة ثابت وموحد أو تقليل معدل التعلم. هذا مفيد إذا كانت البيانات لا تحتاج إلى الكثير من الضبط الدقيق.
• الانخفاض الأسيمبتي: هذه الدالة مفيدة إذا كانت البيانات معقدة وعالية الأبعاد. في مثل هذه الحالات، من الأفضل قضاء المزيد من الوقت في الاستكشاف العالمي قبل الانتقال تدريجياً إلى التفاصيل الدقيقة.
• وظيفة الجوار (NEIGHBORHOOD_FUNC): الخيار الافتراضي لوظيفة الجوار هو الدالة الغاوسية. يتم استخدام دوال أخرى، كما هو موضح أدناه.
• غاوسي (افتراضي): هذه دالة على شكل جرس. يتناقص مدى تحديث الخلايا العصبية بسلاسة كلما زادت المسافة بينها وبين الخلية العصبية الفائزة. يوفر انتقالًا سلسًا ومستمرًا ويحافظ على طوبولوجيا البيانات. إنه مناسب لمعظم الأغراض العامة بسبب سلوكه المستقر والقابل للتنبؤ.
• فقاعة: هذه الوظيفة تنشئ جيرة ثابتة العرض. يتم تحديث جميع الخلايا العصبية داخل هذه الجيرة بشكل متساوٍ، ولا يتم تحديث الخلايا العصبية خارج هذه الجيرة (لنقطة بيانات معينة). إنها أقل تكلفة حسابياً وأسهل في التنفيذ. وهي مفيدة للخرائط الأصغر حيث لا تؤثر الحدود الحادة للجيرة على فعالية التجميع. 
• قبعة مكسيكية: تحتوي على منطقة إيجابية مركزية محاطة بمنطقة سلبية. يتم تحديث الخلايا العصبية القريبة من BMU لتقترب من نقطة البيانات، بينما يتم تحديث الخلايا العصبية البعيدة للتحرك بعيداً عن نقطة البيانات. تعزز هذه التقنية التباين وتوضح الميزات في الخريطة. وبما أنها تبرز المجموعات المتميزة، فهي فعالة في مهام التعرف على الأنماط حيث يكون الفصل الواضح للمجموعات مطلوباً.
• مثلث: هذه الوظيفة تحدد حجم الجوار كمثلث، مع وجود وحدة التحكم الأفضل (BMU) التي لها أكبر تأثير. تتناقص بشكل خطي مع المسافة من وحدة التحكم الأفضل. تُستخدم لتجميع البيانات ذات الانتقالات التدريجية بين المجموعات أو الميزات، مثل بيانات الصور أو الصوت أو السلاسل الزمنية، حيث من المتوقع أن تشترك نقاط البيانات المجاورة في خصائص مشابهة.
• وظيفة المسافة (DISTANCE_FUNC): لقياس المسافة بين الخلايا العصبية ونقاط البيانات، يمكننا اختيار من 4 طرق:
• المسافة الإقليدية (الاختيار الافتراضي): مفيدة عندما تكون البيانات مستمرة، ونريد قياس المسافة في خط مستقيم. تناسب معظم المهام العامة، خاصة عندما تكون نقاط البيانات موزعة بشكل متساوٍ ومرتبطة مكانيًا.
• مسافة الكوسين: خيار جيد للنصوص أو البيانات النادرة عالية الأبعاد حيث تكون الزاوية بين المتجهات أكثر أهمية من المقدار. إنها مفيدة لمقارنة الاتجاه في البيانات.
• مسافة مانهاتن: مثالية عندما تكون نقاط البيانات على شبكة أو مصفوفة (مثل كتل المدن). هذه أقل حساسية للنقاط الشاذة مقارنة بالمسافة الإقليدية.
• مسافة تشيبيشيف: مناسبة للحالات التي يمكن فيها حدوث الحركة في أي اتجاه (مثل، مسافات رقعة الشطرنج). إنها مفيدة للفضاءات المنفصلة حيث نرغب في إعطاء الأولوية لأقصى فرق محوري.
• طوبولوجيا (TOPOLOGY): في شبكة، يمكن ترتيب الخلايا العصبية في هيكل سداسي أو مستطيل: 
• مستطيل (افتراضي): لكل خلية عصبية 4 جيران فوريين. هذا هو الخيار الصحيح عندما لا تحتوي البيانات على علاقة مكانية واضحة. كما أنه أبسط حسابيًا.
• سداسي: لكل خلية عصبية 6 جيران. هذا هو الخيار المفضل إذا كانت البيانات تحتوي على علاقات مكانية يتم تمثيلها بشكل أفضل باستخدام شبكة سداسية. هذه هي الحالة بالنسبة لتوزيعات البيانات الدائرية أو الزاويّة.
• عدد دورات التدريب (N_ITERATIONS): من حيث المبدأ، تؤدي أوقات التدريب الأطول إلى تقليل الأخطاء وتحسين توافق الأوزان مع بيانات الإدخال. ومع ذلك، فإن أداء النموذج يزداد بشكل تقاربي مع عدد التكرارات. وبالتالي، بعد عدد معين من التكرارات، يصبح زيادة الأداء من التفاعلات اللاحقة هامشية فقط. يتطلب تحديد العدد الصحيح من التكرارات بعض التجريب. في هذا الدليل، نقوم بتدريب النموذج على مدى 5000 تكرار. 

لتحديد التكوين الصحيح للمعلمات الفائقة، نوصي بالتجريب مع خيارات متنوعة على مجموعة أصغر من البيانات.

الخاتمة

تعد الخرائط الذاتية التنظيم أداة قوية لـ التعلم غير الخاضع للإشراف. يتم استخدامها للتجميع، وتقليل الأبعاد، واكتشاف الشذوذ، وتصوير البيانات. نظرًا لأنها تحافظ على الخصائص الطوبولوجية للبيانات عالية الأبعاد وتمثلها على شبكة ذات أبعاد أقل، تجعل الخرائط الذاتية التنظيم من السهل تصور وتفسير مجموعات البيانات المعقدة.

تناقش هذه الدروس المبادئ الأساسية للخرائط الذاتية التنظيم وتظهر كيفية تنفيذ خريطة ذاتية التنظيم باستخدام مكتبة MiniSom في بايثون. كما توضح كيفية تحليل النتائج بصريًا وتشرح المعلمات الفائقة المهمة المستخدمة لتدريب الخرائط الذاتية التنظيم وضبط أدائها.