Zelforganiserende Kaarten: Een Intuïtieve Gids met Python Voorbeelden

De omgeving instellen voor SOM

Voordat we de SOM bouwen, moeten we de omgeving voorbereiden met de benodigde pakketten. 

Python-bibliotheken installeren 

We hebben de volgende pakketten nodig: 

• MiniSom is een op NumPy gebaseerde Python-tool die SOM’s creëert en traint. 
• NumPy wordt gebruikt om toegang te krijgen tot wiskundige functies zoals het splitsen van arrays, het verkrijgen van unieke waarden, enz. 
• matplotlib wordt gebruikt om verschillende grafieken en diagrammen te plotten om de gegevens te visualiseren. 
• Het datasets pakket van sklearn wordt gebruikt om datasets te importeren waarop de SOM kan worden toegepast. 
• Het MinMaxScaler pakket van sklearn normaliseert de dataset. 

Het volgende codefragment importeert deze pakketten: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Voorbereiden van de dataset

In deze tutorial gebruiken we MiniSom om een SOM te bouwen en deze vervolgens te trainen op de canonieke IRIS-dataset. Deze dataset bestaat uit 3 klassen irisplanten. Elke klas heeft 50 instanties. Om de gegevens voor te bereiden, volgen we deze stappen: 

• Importeer de Iris-dataset vanuit sklearn, 
• Haal de gegevensvectoren en de doelscalars eruit. 
• Normaliseer de datavectoren. In deze tutorial gebruiken we de MinMaxScaler van scikit-learn.
• Declareer een set labels voor elk van de drie klassen van Iris-planten.

De volgende code implementeert deze stappen:

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Implementatie van Zelforganiserende Kaarten (SOM) in Python

Om een SOM in Python te implementeren, definiëren en initialiseren we het raster voordat we het trainen op de dataset. We kunnen vervolgens de getrainde neuronen en de geclustere dataset visualiseren.

Definiëren van het SOM-raster

Zoals eerder uitgelegd, is een SOM een raster van neuronen. Met MiniSom kunnen we 2-dimensionale rasters maken. De X- en Y-dimensies van het raster zijn het aantal neuronen langs elke as. Om het SOM-raster te definiëren, moeten we ook het volgende specificeren:

• De X- en Y-dimensies van het raster
• Het aantal invoervariabelen – dit is het aantal datarijen.

Declareer deze parameters als Python-constanten:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

De onderstaande voorbeeldcode illustreert hoe je het raster kunt declareren met MiniSom:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

De eerste twee parameters zijn het aantal neuronen langs de X- en Y-assen, en de derde parameter is het aantal variabelen.

We verklaren andere parameters en hyperparameters tijdens het creëren van het SOM-raster. We zullen deze later in de tutorial uitleggen. Voor nu, verklaar deze parameters zoals hieronder weergegeven:

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Maak een SOM met deze parameters:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Initialiseren van de neuronen

De bovenstaande opdracht creëert een SOM met willekeurige gewichten voor alle neuronen. Het initialiseren van de neuronen met gewichten uit de gegevens (in plaats van willekeurige getallen) kan het trainingsproces efficiënter maken.

Bij het gebruik van MiniSom om een Zelf-Organiserende Kaart (SOM) te maken, zijn er twee manieren om de gewichten van de neuronen op basis van de gegevens te initialiseren:

• Willekeurige initialisatie: De initiële gewichten van de neuronen worden willekeurig getrokken uit de invoergegevens. Dit doen we door de .random_weights_init() functie toe te passen op de SOM. 
• PCA-initialisatie: Principal Component Analysis (PCA) initialisatie gebruikt de hoofdcomponenten van de invoergegevens om de gewichten te initialiseren. De initiële gewichten van de neuronen bestrijken de eerste twee hoofdcomponenten. Dit leidt vaak tot snellere convergentie.

In deze gids gebruiken we PCA-initialisatie. Om PCA-initialisatie op de SOM-gewichten toe te passen, gebruik de .pca_weights_init() functie zoals hieronder weergegeven:

som.pca_weights_init(data)

Training van de SOM

Het trainingsproces werkt de SOM-gewichten bij om de afstand tussen de neuronen en de datapunten te minimaliseren.

Hieronder leggen we het iteratieve trainingsproces uit:

• Initialisatie: De gewichtsvectoren van alle neuronen worden geïnitialiseerd, meestal met willekeurige waarden. Het is ook mogelijk om de gewichten te initialiseren door de distributie van de invoergegevens te bemonsteren.
• Invoerselectie: Een invoervector wordt (willekeurig) geselecteerd uit de trainingsdataset.
• BMU-identificatie: De neuron met de gewichtvector die het dichtst bij de invoervector ligt, wordt geïdentificeerd als de BMU.
• Buurtupdate: De BMU en zijn naburige neuronen actualiseren hun gewichtsvectoren. De leersnelheid en de buurtfunctie bepalen welke neuronen worden bijgewerkt en met hoeveel. Bij de iteratiestap t, gegeven de ingangsvector x, de gewichtsvector van neuron i als w_i, de leersnelheid (t), en de buurtfunctie h_bi (deze functie kwantificeert de mate van update voor neuron i gegeven de BMU-neuron b), wordt de gewichtsupdateformule voor neuron i als volgt weergegeven:
• Vervalssnelheid van de leerparameter en buurtstraal: Zowel de leerparameter als de buurtstraal nemen in de loop van de tijd af. In de eerdere iteraties maakt het trainingsproces grotere aanpassingen over een groter gebied. Latere iteraties helpen de gewichten te verfijnen door kleinere veranderingen aan te brengen in de gewichten van aangrenzende neuronen. Dit stelt de kaart in staat om te stabiliseren en te convergeren.

Om de SOM te trainen, presenteren we het model de invoergegevens. We kunnen kiezen uit een van de twee benaderingen om dit te doen:

• Kies willekeurig monsters uit de invoergegevens. De .train_random() functie implementeert deze techniek.
• Voer de vectoren in de invoergegevens sequentieel uit. Dit wordt gedaan met de .train_batch() functie.

Deze functies accepteren de invoergegevens en het aantal iteraties als parameters. In deze gids gebruiken we de .train_random() functie. Verklaar het aantal iteraties als een constante en geef het door aan de trainingsfunctie:

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

Na het uitvoeren van het script en het voltooien van de training, wordt er een bericht met de kwantisatiefout weergegeven:

quantization error: 0.05357240680504421 

De kwantisatiefout geeft de hoeveelheid informatie aan die verloren gaat wanneer de SOM de gegevens kwantiseert (de dimensionaliteit van de gegevens vermindert). Een grote kwantisatiefout duidt op een grotere afstand tussen de neuronen en de gegevenspunten. Het betekent ook dat de clustering minder betrouwbaar is.

Visualiseren van SOM-neuronen

We hebben nu een getraind SOM-model. Om het te visualiseren, gebruiken we een afstandskaart (ook bekend als een U-matrix). De afstandskaart toont de neuronen van de SOM als een raster van cellen. De kleur van elke cel vertegenwoordigt de afstand tot de naburige neuronen.

De afstandskaart is een raster met dezelfde afmetingen als de SOM. Elke cel in de afstandskaart is de genormaliseerde som van de (Euclidische) afstanden tussen een neuron en zijn buren.

Open de SOM-afstandskaart met behulp van de functie .distance_map(). Om de U-matrix te genereren, volgen we deze stappen:

• Gebruik pyplot om een figuur te maken met dezelfde dimensies als de SOM. In dit voorbeeld zijn de dimensies 8×8.
• Plot de afstands
• Geef de colorbar, een index die verschillende kleuren toewijst aan verschillende scalaire waarden. In dit geval variëren de scalaire afstandswaarden van 0 tot 1.

De onderstaande code voert deze stappen uit:

# maak het rooster
plt.figure(figsize=(8, 8))
# plot de afstandskaart
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# toon de kleurenbalk
plt.colorbar()
plt.show()

In dit voorbeeld maakt de U-matrix gebruik van een monotone kleurenschema. Het kan worden begrepen aan de hand van deze richtlijnen:

• Lichtere tinten vertegenwoordigen dicht bij elkaar gelegen neuronen, en donkerdere tinten vertegenwoordigen neuronen die verder van elkaar verwijderd zijn.
• Groepen van lichtere tinten kunnen worden geïnterpreteerd als clusters. Donkere knooppunten tussen de clusters kunnen worden geïnterpreteerd als de grenzen tussen clusters.

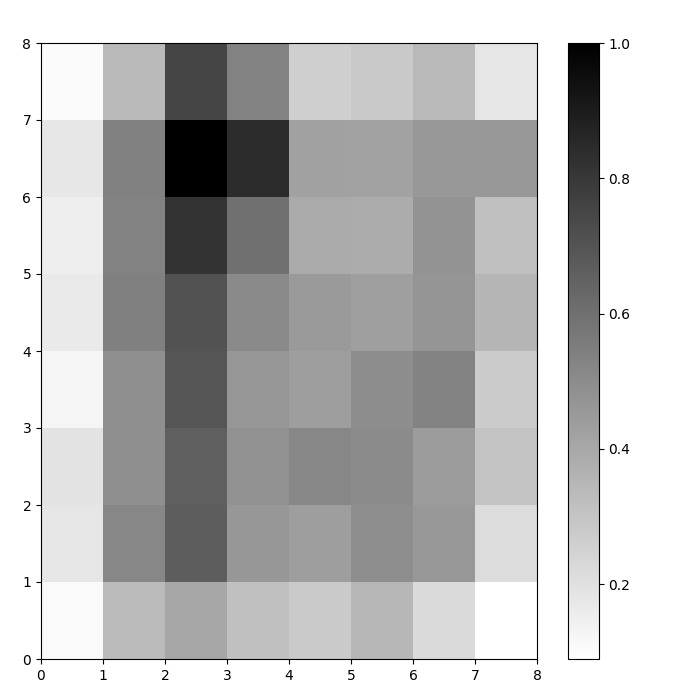
Figuur 1: U-matrix van SOM getraind op de Iris dataset (afbeelding door auteur)

Evaluatie van de SOM Clustering Resultaten

De vorige figuur heeft grafisch de neuronen van de SOM geïllustreerd. In dit gedeelte laten we zien hoe we kunnen visualiseren hoe de SOM de gegevens heeft geclusterd.

Identificatie van clusters

We leggen markers over de bovenstaande U-matrix om aan te geven welke klasse van Iris plant elke cel (neuron) vertegenwoordigt. Om dit te doen:

• Maak zoals voorheen een 8×8 figuur met pyplot, plot de afstandskaart en toon de kleurenbalk. 
• Geef een array van drie matplotlib markers, één voor elke klasse van de Iris-plant. 
• Geef een array van drie matplotlib kleurcodes, één voor elke klasse van de Iris-plant. 
• Plot iteratief de winnende neuron voor elk datapunt:
• Bepaal de (coördinaten van de) winnende neuron voor elk datapunt met behulp van de .winner() functie.
• Plot de positie van elke winnende neuron in het midden van elke cel op het raster. w[0] en w[1] geven respectievelijk de X- en Y-coördinaten van de neuron. Er wordt 0,5 aan elke coördinaat toegevoegd om deze in het midden van de cel te plotten.

De onderstaande code laat zien hoe je dit doet:

# plot de afstandskaart
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# maak de markeringen en kleuren voor elke klasse
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# plot de winnende neuron voor elk datapunt
for count, datapoint in enumerate(data):
    # haal de winnaar op
    w = som.winner(datapoint)  
    # plaats een marker op de winnende positie voor het monster datapunt
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

De resulterende afbeelding wordt hieronder weergegeven: 

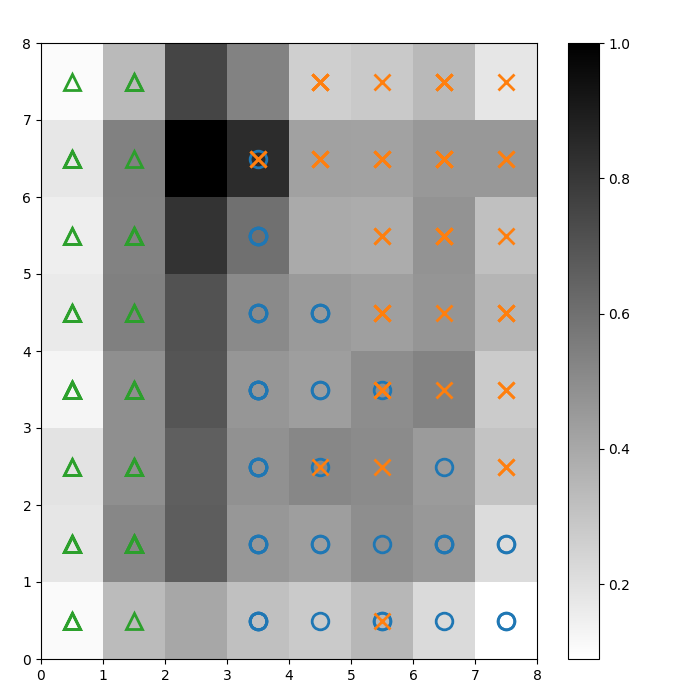
Figuur 2: U-matrix met klasse markers (afbeelding door auteur)

Gebaseerd op de Iris dataset documentatie, “één klasse is lineair scheidbaar van de andere 2; de laatste zijn niet lineair scheidbaar van elkaar”. In de bovenstaande U-matrix worden deze drie klassen vertegenwoordigd door drie markers – driehoek, cirkel en kruis. 

Merk op dat er geen duidelijke grens is tussen de blauwe cirkels en de oranje kruisen. Bovendien zijn er twee klassen over elkaar heen gelegd op dezelfde neuron in veel cellen. Dit betekent dat de neuron equidistant is van beide klassen. 

Visualiseren van de clustering uitkomst

Een SOM is een clusteringmodel. Vergelijkbare datapunten worden aan dezelfde neuron toegewezen. Datapunten van dezelfde klasse worden toegewezen aan een cluster van naburige neuronen. We plotten alle datapunten op het SOM-rooster om het clusteringgedrag beter te bestuderen.

De volgende stappen beschrijven hoe je deze spreidingsgrafiek kunt maken:

• Krijg de X- en Y-coördinaten van de winnende neuron voor elk dat punt.
• Plot de afstandskaart, zoals we deden voor Figuur 1.
• Gebruik plt.scatter() om een scatterplot te maken van alle winnende neuronen voor elk datapunt. Voeg een willekeurige offset toe aan elk punt om overlappingen tussen datapunten binnen dezelfde cel te voorkomen.

We implementeren deze stappen in de onderstaande code: 

# verkrijg de X- en Y-coördinaten van de winnende neuron voor elk datapuntw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# plot de afstandskaart
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# maak een scatterplot van alle winnende neuronen voor elk datapunt
# voeg een willekeurige offset toe aan elk punt om overlappingen te voorkomen
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

De volgende grafiek toont de uitvoer scatterplot:

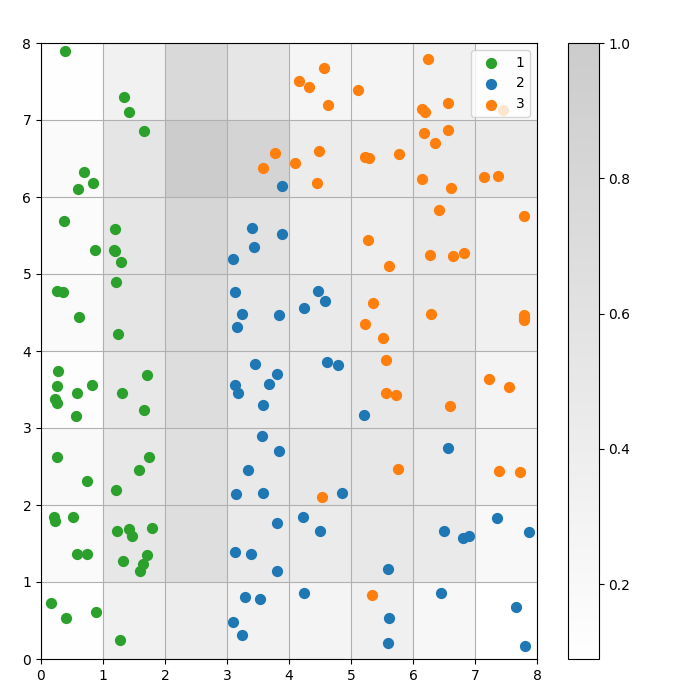Figuur 3: Spreidingsdiagram van gegevenspunten binnen cellen (afbeelding door de auteur)

Let op het volgende in het bovenstaande spreidingsdiagram: 

• Sommige cellen bevatten zowel blauwe als oranje stippen. 
• De groene stippen zijn duidelijk gescheiden van de rest van de gegevens, maar de blauwe en oranje stippen zijn niet netjes gescheiden. 
• De bovenstaande observaties komen overeen met het feit dat slechts één van de drie clusters in de Iris-dataset een duidelijke grens heeft.
• In Figuur 1 komen donkere knooppunten tussen de clusters (die geïnterpreteerd kunnen worden als de grenzen tussen clusters) overeen met lege cellen in de spreidingsdiagram.

Je kunt de complete code openen en uitvoeren op dit DataLab-notebook.

Het afstemmen van het SOM-model

De vorige secties toonden aan hoe je een SOM-model kunt creëren en trainen en hoe je de resultaten visueel kunt bestuderen. In deze sectie bespreken we hoe je de prestaties van SOM-modellen kunt afstemmen.

Belangrijke hyperparameters om af te stemmen

Zoals bij elk machine learning model hebben hyperparameters een aanzienlijke impact op de prestaties van het model.

Enkele van de belangrijke hyperparameters bij het trainen van SOMs zijn:

• De rooster grootte bepaalt de grootte van de kaart. Het aantal neuronen in een kaart met een rooster grootte van AxB is A*B.
• De leer snelheid bepaalt hoeveel de gewichten in elke iteratie worden aangepast. We stellen de initiële leer snelheid in, en deze neemt in de loop van de tijd af volgens de verouderingsfunctie.
• De verouderingsfunctie bepaalt in welke mate de leer snelheid in elke volgende iteratie wordt verlaagd.
• De buurtfunctie is een wiskundige functie die aangeeft welke neuronen als de buren van de BMU moeten worden beschouwd.
• De standaarddeviatie specificeert de spreiding van de buurtfunctie. Bijvoorbeeld, een Gaussian buurtfunctie met een hoge standaarddeviatie zal een grotere buurt hebben dan dezelfde functie met een lagere standaarddeviatie. We stellen de initiële standaarddeviatie in, die in de loop van de tijd afneemt volgens de sigma-afnamefunctie.
• De sigma-afname functie bepaalt hoeveel de standaardafwijking wordt verlaagd in elke volgende iteratie. 
• Het aantal trainingsiteraties bepaalt hoe vaak de gewichten worden bijgewerkt. In elke trainingsiteratie worden de neuronengewichten eenmaal bijgewerkt. 
• De afstandsfunctie is een wiskundige functie die de afstand tussen neuronen en datapunten berekent. 
• De topologie bepaalt de indeling van de rasterstructuur. De neuronen in het raster kunnen in een rechthoekig of hexagonaal patroon worden gerangschikt. 

In de volgende sectie bespreken we richtlijnen voor het instellen van de waarden van deze hyperparameters. 

Impact van hyperparameterafstemming

Hyperparameterwaarden moeten worden vastgesteld op basis van het model en de dataset. Tot op zekere hoogte is het bepalen van deze waarden een proces van trial and error. In deze sectie geven we richtlijnen voor het afstemmen van elke hyperparameter. Naast elke hyperparameter vermelden we (tussen haakjes) de respectieve Python-constanten die in de voorbeeldcode worden gebruikt.

• Rastergrootte (SOM_X_AXIS_NODES en SOM_X_AXIS_NODES): De rastergrootte hangt af van de grootte van de dataset. De vuistregel is dat, gegeven een dataset van grootte N, het raster ongeveer 5*sqrt(N) neuronen zou moeten bevatten. Bijvoorbeeld, als de dataset 150 monsters heeft, zou het raster 5*sqrt(150) = ongeveer 61 neuronen moeten bevatten. In deze tutorial heeft de Iris-dataset 150 rijen en gebruiken we een raster van 8×8.
• Initiële leersnelheid (ALPHA): Een hogere snelheid versnelt de convergentie, terwijl lagere snelheden worden gebruikt voor fijnere aanpassingen na de vroege iteraties. De initiële leersnelheid moet groot genoeg zijn om snelle aanpassing mogelijk te maken, maar niet zo groot dat het optimale gewichtswaarden overschiet. In dit artikel is de initiële leersnelheid 0.5.
• Initiële standaardafwijking (SIGMA0): Het bepaalt de initiële grootte of spreiding van de buurt. Een grotere waarde overweegt meer globale patronen. In dit voorbeeld gebruiken we een startstandaardafwijking van 1.5.
• Voor de vervalratio (DECAY_FUNC) en de sigma vervalratio (SIGMA_DECAY_FUNC), kunnen we kiezen uit een van de drie soorten vervalfuncties: 
• Inverse vervalings: Deze functie is geschikt als de gegevens zowel globale als lokale patronen hebben. In dergelijke gevallen hebben we een langere fase van brede leren nodig voordat we ons op lokale patronen concentreren.
• Lineaire verval: Dit is goed voor datasets waarbij we een constante en uniforme buurtgrootte of afname van de leersnelheid willen. Dit is nuttig als de gegevens niet veel fijn-afstemming nodig hebben.
• Asymptotisch verval: Deze functie is nuttig als de gegevens complex en hoog-dimensionaal zijn. In dergelijke gevallen is het beter om meer tijd te besteden aan globale verkenning voordat we geleidelijk overgaan naar fijnere details.
• Buurtfunctie (BUURT_FUNC): De standaardkeuze voor de buurtfunctie is de Gaussische functie. Andere functies, zoals hieronder uitgelegd, worden ook gebruikt.
• Gaussiaans (standaard): Dit is een klokvormige curve. De mate waarin een neuron wordt bijgewerkt, neemt geleidelijk af naarmate de afstand tot het winnende neuron toeneemt. Het biedt een soepele en continue overgang en behoudt de topologie van de gegevens. Het is geschikt voor de meeste algemene doeleinden vanwege het stabiele en voorspelbare gedrag.
• Bubbel: Deze functie creëert een buurt met een vaste breedte. Alle neuronen binnen deze buurt worden gelijkmatig bijgewerkt, en neuronen buiten deze buurt worden niet bijgewerkt (voor een gegeven datapunt). Het is computationeel goedkoper en gemakkelijker te implementeren. Het is nuttig voor kleinere kaarten waar scherpe grenzen van de buurt de effectieve clustering niet in gevaar brengen.
• Mexicaanse hoed: Het heeft een centrale positieve regio omringd door een negatieve regio. Neuronen dicht bij de BMU worden bijgewerkt om dichter bij het datapunt te komen, en neuronen verder weg worden bijgewerkt om zich van het datapunt te verwijderen. Deze techniek verbetert het contrast en scherpt de kenmerken in de kaart aan. Aangezien het onderscheidende clusters benadrukt, is het effectief in taken voor patroonherkenning waar een duidelijke scheiding van clusters gewenst is.
• Driehoek: Deze functie definieert de buurtgrootte als een driehoek, waarbij de BMU de grootste invloed heeft. Het neemt lineair af met de afstand van de BMU. Het wordt gebruikt voor het clusteren van gegevens met geleidelijke overgangen tussen clusters of kenmerken, zoals afbeelding, spraak of tijdreeksgegevens, waarbij verwante gegevenspunten worden verwacht vergelijkbare kenmerken te delen.
• Afstandsfunctie (DISTANCE_FUNC): Om de afstand tussen neuronen en gegevenspunten te meten, kunnen we kiezen uit 4 methoden:
• Euclidische afstand (standaardkeuze): Nuttig wanneer de gegevens continu zijn en we de rechtstreekse afstand willen meten. Het is geschikt voor de meeste algemene taken, vooral wanneer gegevenspunten gelijkmatig verdeeld en ruimtelijk gerelateerd zijn.
• Cosinusafstand: Goede keuze voor tekst of hoge-dimensionale spaarzame gegevens waarbij de hoek tussen vectoren belangrijker is dan de grootte. Het is nuttig voor het vergelijken van de richting in gegevens.
• Manhattan afstand: Ideaal wanneer gegevenspunten op een raster of rooster staan (bijv. stadsblokken). Dit is minder gevoelig voor uitschieters dan Euclidische afstand.
• Chebyshev-afstand: Geschikt voor situaties waarin beweging in elke richting kan plaatsvinden (bijv. schaakbordafstanden). Het is nuttig voor discrete ruimtes waar we de maximale asverschil willen prioriteren.
• Topologie (TOPOLOGY): In een rooster kunnen neuronen worden gerangschikt in een hexagonale of rechthoekige structuur: 
• Rechthoekig (standaard): elke neuron heeft 4 directe buren. Dit is de juiste keuze wanneer de gegevens geen duidelijke ruimtelijke relatie hebben. Het is ook computationeel eenvoudiger.
• Hexagonaal: elke neuron heeft 6 buren. Dit is de voorkeur optie als de gegevens ruimtelijke relaties hebben die beter worden weergegeven met een hexagonale raster. Dit is het geval bij cirkelvormige of hoekige gegevensdistributies.
• Aantal trainingsiteraties (N_ITERATIONS): In principe leiden langere trainingstijden tot lagere fouten en een betere afstemming van de gewichten op de invoergegevens. De prestaties van het model nemen echter asymptotisch toe met het aantal iteraties. Na een bepaald aantal iteraties is de prestatieverbetering van daaropvolgende interacties slechts marginaal. Het bepalen van het juiste aantal iteraties vergt enige experimentatie. In deze tutorial trainen we het model over 5000 iteraties.

Om de juiste configuratie van hyperparameters te bepalen, raden we aan om te experimenteren met verschillende opties op een kleiner subset van de gegevens.

Conclusie

Zelforganiserende kaarten zijn een robuust hulpmiddel voor onbegeleid leren. Ze worden gebruikt voor clustering, dimensionale reductie, anomaliedetectie en datavisualisatie. Aangezien ze de topologische eigenschappen van hoog-dimensionele data behouden en deze op een lager-dimensionaal rooster weergeven, maken SOM’s het gemakkelijk om complexe datasets te visualiseren en te interpreteren.

Deze tutorial besprak de onderliggende principes van SOM’s en toonde aan hoe je een SOM kunt implementeren met de MiniSom Python-bibliotheek. Het demonstreerde ook hoe je de resultaten visueel kunt analyseren en legde de belangrijke hyperparameters uit die worden gebruikt om SOM’s te trainen en hun prestaties te optimaliseren.