隨機步驟：探索隨機漫步模型

在大學裡我參加了第一門以編碼為基礎的統計學課程，我的老師提出了一個問題：我們如何模擬水盤中單一花粉粒子的布朗運動？經過幾次錯誤的嘗試，我和同學最終找到了正確答案：隨機漫步。後來我了解到，這個簡單的模型被用來模擬各種事物，從動物運動到股票價格波動。

在這篇文章中，我們將探索隨機漫步的數學基礎，檢視不同類型，並討論它們的應用。使隨機漫步有趣的部分之一是它在許多不同學科中被使用。除了我的例子，物理學中它有助於描述粒子運動；在金融中，它模擬股票價格波動；在生物學中，它解釋動物運動模式。隨機漫步捕捉現實世界的隨機性，這對於模擬隨機過程至關重要。

對於那些希望在支撐隨機漫步理論的統計學方面建立堅實基礎的人，我們建議從《R中的統計學介紹》課程或《Python中的統計學介紹》課程開始。

隨機漫步是什麼？

在概率理論中，隨機漫步是描述由隨機步驟組成的路徑的模型。換句話說，隨機漫步是描述由一系列步驟組成的路徑的數學模型，每個步驟獨立且具有一定的概率。這種隨機性使得隨機漫步天生難以預測。

想像一個人每個時刻都會朝著隨機方向邁出一步。隨著時間的推移，他們的路徑形成一條難以預測的蜿蜒小徑。儘管概念簡單，但這個概念具有出人意料的深度和多樣性，可以模擬涉及隨機性的各種現實情景。

隨機漫步的概念性解釋。圖片由 napkin.ai 提供。

隨機漫步的概念可以追溯到早期的概率研究。其中一個最早的例子，常被稱為醉漢漫步，說明了一個隨機移動的人不會按照可預測的方式朝著目的地前進，而是會表現出不規則的遊走。這種隨機性，再加上每一步都獨立於先前步驟的假設，奠定了現代隨機漫步模型的基礎。

理解隨機漫步的數學

為了理解隨機漫步，讓我們從一個簡單的情況開始：一維（1D）隨機漫步。想像在數線上有一粒粒子。每一步可以向數線上的+1或-1移動。每次移動都由向右或向左的等概率決定。隨著時間推移，粒子的位置形成一個分佈，代表著在不同位置找到它的可能性。

這個原則可以擴展到二維或三維。在二維（2D）隨機行走中，粒子在平面上移動，可以向四個基本方向（上、下、左、右）中的任何一個等概率地前進。同樣，在三維（3D）隨機行走中，粒子在空間中移動，可以向六個可能的方向（上、下、左、右、前、後）中的任何一個等概率地前進。這些高維度的隨機行走捕捉了更加複雜和現實的情況。

隨機行走的一個特點是其隨機性，意味著每一步只取決於當前位置，而不取決於之前的步驟。這使它們成為馬爾可夫過程的一種類型——一種數學概念，其中未來狀態僅取決於當前狀態，而不取決於前面發生的事件序列。這種“無記憶”的移動，結合描述潛在位置的概率分佈，為理解隨機行走提供了堅實的數學基礎。

我們可以使用統計特性來分析隨機漫步，以了解其隨時間的行為。這涉及檢查期望的距離（從起點），可能位置的概率分佈以及回到原點的可能性等方面。這些分析幫助我們量化隨機性和可預測性，提供對模式的洞察並進行預測。

隨機漫步的關鍵特性

隨機漫步具有幾個重要特性，幫助我們理解它們的行為和應用。以下是一些重要方面需要考慮：

期望和方差

在一維隨機漫步中，我們可以計算從起點到時間的期望距離（或平均位置）。如果每一步都有相等的概率向左或向右移動，則經過許多步驟後的期望位置仍然為零，這意味著平均而言，行走者保持在起點附近。

然而，位置的變異性隨著每一步增加，這衡量可能位置的散佈或分散程度也會增加。具體來說，在對稱隨機漫步中，變異性隨著步數呈線性增長，使其成為一個衡量隨著時間從原點的典型距離的有用指標。

自相關

儘管簡單隨機漫步之間沒有相關性（每一步與上一步無關），但某些類型的隨機漫步會引入自相關，過去的步驟可以影響未來的步驟。例如，在偏向性隨機漫步中，步驟可能稍微朝向一個方向，導致位置更容易預測。

隨機漫步中的自相關影響了我們對漫步進展的建模和預測。這在過去行為影響未來步驟的應用中尤為重要，例如某些金融模型。

中心極限定理

中央極限定理（CLT）告訴我們，大量獨立隨機變數的總和趨向於遵循正態（或高斯）分佈，而不受原始分佈的影響。在隨機漫步的背景下，這意味著隨著步數的增加，位置的分佈趨向於類似正態分佈。這是一個有用的特性，因為它使我們能夠近似計算在特定距離處找到行走者的概率。

大數法則

大數法則（LLN）解釋了隨著試驗或步數的增加，結果的平均值將收斂到真實平均值。對於隨機漫步來說，這意味著雖然平均位置保持為零，但隨著每一步的增加，位置的變異性和可能位置的範圍將可預測地增加。這一原則有助於在大樣本中純隨機性和可預測的統計規律之間建立橋樑。

隨機漫步的類型

隨機漫步根據規則的不同而變化很大。這些類型影響著漫步的行為。有些設計用於簡單或結構化環境，而其他一些則適用於更複雜的現實世界現象。讓我們探索一些最常見的隨機漫步類型。

1D、2D和3D隨機漫步

隨機漫步的維度在其行為中起著基本作用。在1D隨機漫步中，每一步都是沿著一條線向前或向後移動。這使得漫步相對容易建模和預測。

然而，當我們轉向2D（平面）和3D（空間）漫步時，可能的路徑數量顯著增加，引入新的行為。例如，在2D隨機漫步中，返回起點的概率仍然很高，而在3D隨機漫步中，這個概率下降。

這種變化在物理學和化學等領域非常重要，因為粒子的擴散可能會根據尺寸的限制而有所不同。

晶格隨機行走

在晶格隨機行走中，移動被限制在網格或晶格上的離散點上。這種類型的行走在物理學和網絡理論中常被使用，其中節點被排列在網格上，移動僅限於相鄰節點。

一個常見的例子是2D晶格，每一步都允許在笛卡爾座標上移動到相鄰點。這種限制通過限制移動路徑來簡化建模，當模擬復雜的網絡或分子結構時非常有用。

高斯隨機行走

在高斯隨機漫步中，每一步的大小由高斯（或正態）分佈決定。步伐大小不固定，而是根據一個呈鐘形曲線分佈的概率分配，大多數步伐很小，偶爾會有較大的跳躍。這種漫步在金融建模中經常用於解釋資產價格變動的變異性。

異質性和偏向性隨機漫步

異質性和偏向性隨機漫步允許根據某些概率來變化步伐方向和大小。這種靈活性使它們更適應現實情況。

在異質性隨機漫步中，根據位置或外部條件，移動至任何方向的概率可能會改變。例如，尋找食物的動物可能偏好已知資源豐富的區域，形成一種偏向性隨機漫步。這些漫步對於研究依賴於情境因素的行為很有用。

帶漂移的隨機漫步

在有漂移的隨機遊走中，存在一致的趨勢會向一個方向移動。例如，股票價格可能會在時間上呈現整體上升趨勢，儘管每天會有波動。這些遊走中的漂移代表著影響路徑的外部力量或趨勢。這種類型在金融領域中經常可見，模型會納入漂移項來表示增長或下降，從而提供更現實的方法來預測資產價格和市場趨勢。

這些隨機遊走類型各有其獨特用途，提供不同的方式來建模隨機但有結構的行為。尺度約束、步驟分佈以及漂移或偏差的存在使得隨機遊走非常適用於跨領域的數據建模和模擬。

隨機遊走的現實應用

隨機遊走不僅僅是理論概念；它們在許多學科中的實際應用中發揮著重要作用。讓我們探索隨機遊走如何在各個領域中的真實問題解決中發揮作用。

在數據科學和機器學習中的應用

計算機科學

隨機遊走是一些計算機科學算法的基礎，例如隨機取樣、網絡圖遍歷和圖像分割。例如，谷歌的 PageRank 算法使用隨機遊走來根據相關性對網頁進行排名，模擬用戶在互聯網上隨機導航到鏈接之間的方式。

特徵提取

在機器學習中，隨機遊走可以通過突出數據點之間的關係來幫助提取特徵。例如，在網絡分析中，隨機遊走可以揭示集群或社區，有助於推薦系統和社交網絡分析等任務。

異常檢測

隨機遊走還可以用於檢測數據集中的異常。例如，如果數據點在隨機遊走模型中明顯偏離典型路徑，則這些點可能表明數據中的異常事件或錯誤。在領域如網絡安全和欺詐檢測中，異常檢測尤為重要。

模擬隨機過程

隨機遊走模擬隨機或隨機決定的過程，讓數據科學家能夠模擬不可預測的現實世界現象。通過模擬隨機遊走，我們可以深入了解精確預測具有挑戰性的系統，例如天氣模式或客戶行為。

時間序列預測

在時間序列分析中，隨機遊走為某些預測模型奠定基礎，包括金融中的隨機遊走假設。這些模型假設時間序列中的未來值僅取決於最近的值，與過去趨勢無關。欲了解更多有關時間序列預測的信息，請查看ARIMA 時間序列預測：完整指南。此外，參加我們的R 中的預測課程，由 Hyndman 教授講授，將隨機遊走模型與天真和季節性天真預測方法相連接。

其他領域中的應用

金融

隨機漫步最著名的應用之一是在金融建模中，特別是用於預測股票價格。有效市場假說表明，股價波動基本上是隨機的，因為新信息會立即被吸收，使未來價格變得難以預測。隨機漫步可以用來模擬隨時間變化的股價變化，說明價格如何在沒有可預測路徑的情況下波動。

數學

在純數學中，隨機漫步提供了解決複雜問題的方法。例如，它們在解Laplace方程、分析網絡和探索組合數學方面非常有用。

物理和化學

在物理科學中，隨機漫步對於建模擴散過程至關重要，例如分子在媒介中傳播的方式。布朗運動是一個經典示例，其中懸浮在流體中的粒子由於與周圍分子的碰撞而不可預測地移動，可以使用隨機漫步進行準確模擬。這實際上是我第一次了解隨機漫步的方式。

生物學

隨機漫步在生態學中對於研究動物運動模式非常有價值。尋找資源的動物可能看起來像在進行隨機漫步，有時會偏向於已知資源豐富的區域。其他生物學概念，例如人口或基因的擴散，通常可以用隨機漫步原則建模，這使得更容易理解和預測生態系統內的變化。

隨機漫步的特殊情況和變體

除了經典的隨機漫步外，還有幾種高級變體將這一概念擴展以適應專門應用。

避免自交的漫步

避免自交的漫步是一種隨機漫步，其中路徑不會重複經過已經通過的位置。這種變體在聚合物化學等領域特別有用，可以模擬聚合物鏈如何形成而不相交。由於每一步都會避免之前訪問過的點，避免自交的漫步比傳統隨機漫步更受限制。這意味著它們在計算上具有挑戰性，但對於理解受限空間中不重疊路徑很有用。

分支

在分支隨機漫步中，路徑可以分裂成多個分支，每個分支都遵循一個隨機漫步。這種類型的漫步在建模細胞分裂或信息在網絡中傳播等分支過程中起到重要作用。每個“分支”代表著一條從共同來源發出的獨立隨機路徑。

相關漫步

相關漫步將這一概念推向更深入，其中每一步的方向部分受到前一步的影響。這種變體對於模擬系統中變化逐漸而非隨機發生的慣性很有用。相關漫步通常應用於金融領域來模擬價格趨勢，或應用於運動生態學中理解動物如何在環境中導航，並具有對過去方向的一定記憶。

擦除迴圈的漫步

擦除迴圈的漫步是一種變體，其中迴圈或交叉自身的路徑在形成時被移除。每次步驟重新訪問一個位置時，介於其中的迴圈將被擦除，留下一條簡化的、不重複的路徑。擦除迴圈的漫步通常應用於網絡分析和迷宮生成算法，因為它們創建的路徑避免了冗余。

在Python中實現隨機漫步

讓我們嘗試在Python中實現一個隨機漫步。要開始，請確保已安裝Python（我們將使用Python 3.10）並且具有必要的庫。您可以使用pip安裝任何缺少的庫。這是我們將使用的內容：

import numpy as np # 用於數值操作和生成隨機步驟
import matplotlib.pyplot as plt # 用於繪圖和可視化隨機漫步

1D隨機漫步

我們將從一維簡單的隨機漫步開始，每一步都是隨機選擇的+1或-1。

# 參數
n_steps = 100  # 步數

# 生成隨機步驟：+1或-1
steps = np.random.choice([-1, 1], size=n_steps)

# 計算位置
positions = np.cumsum(steps)

# 繪製隨機漫步
plt.figure(figsize=(10, 6))
plt.plot(positions, marker='o', linestyle='-', markersize=4)
plt.title("1D Random Walk")
plt.xlabel("Step")
plt.ylabel("Position")
plt.grid(True)
plt.show()

這會生成一個簡單的隨機遊走並可視化隨時間的變化。運行此代碼時，輸出如下：

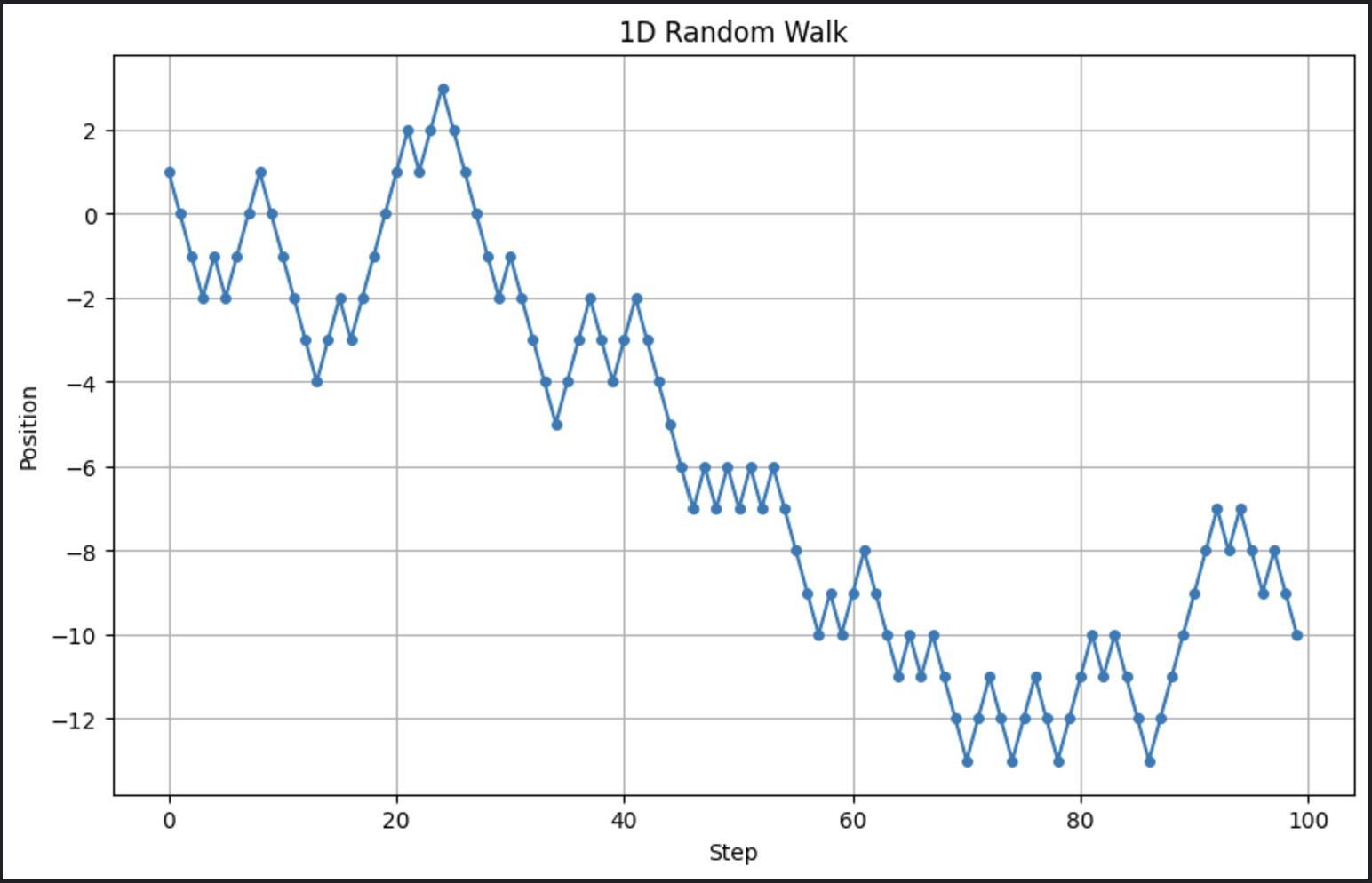
現在請記住，我們正在運行一個隨機模型。這意味著每次運行時，輸出會有些許不同。

2D隨機遊走

現在讓我們將隨機遊走擴展到兩個維度。每一步中，方向將被隨機選擇。

# 參數
n_steps = 500

# 在x和y方向生成隨機步驟
x_steps = np.random.choice([-1, 1], size=n_steps)
y_steps = np.random.choice([-1, 1], size=n_steps)

# 計算位置
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# 繪製2D隨機遊走
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # 起始點紅色點
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # 結束點黑色點
plt.title("2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # 確保兩軸等比例
plt.legend()
plt.show()

這段程式碼在二維空間中創建了一條視覺上引人入勝的路徑。

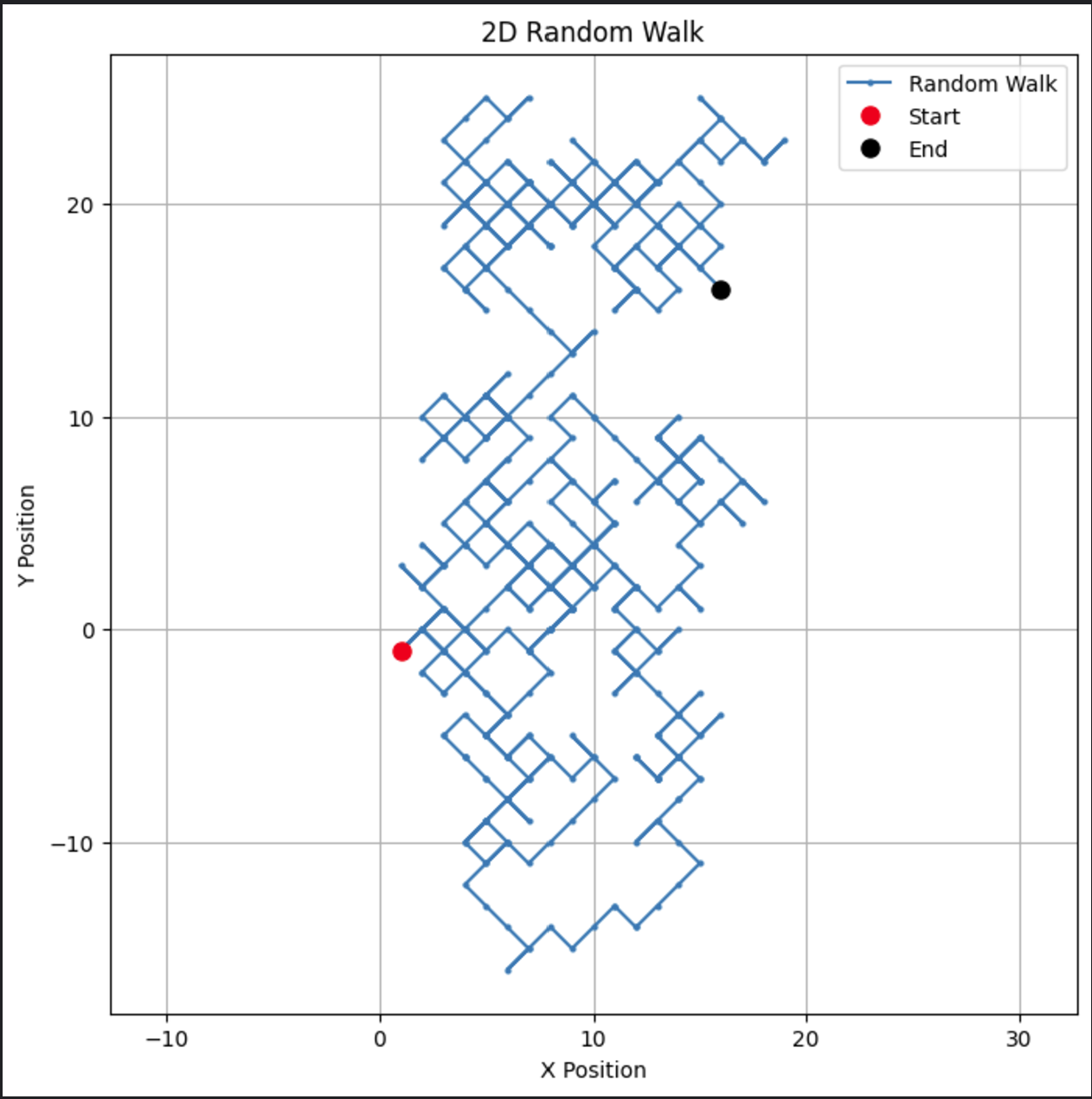
這種二維隨機運動的類型可以修改以適應粒子運動或空間建模等應用。

有偏向性的隨機運動

最後，讓我們看一個稍微複雜的例子：有偏向性的隨機運動。為了引入偏向性，我們可以調整每個步驟方向的概率。例如，我們可能會使向上的步驟更有可能發生。

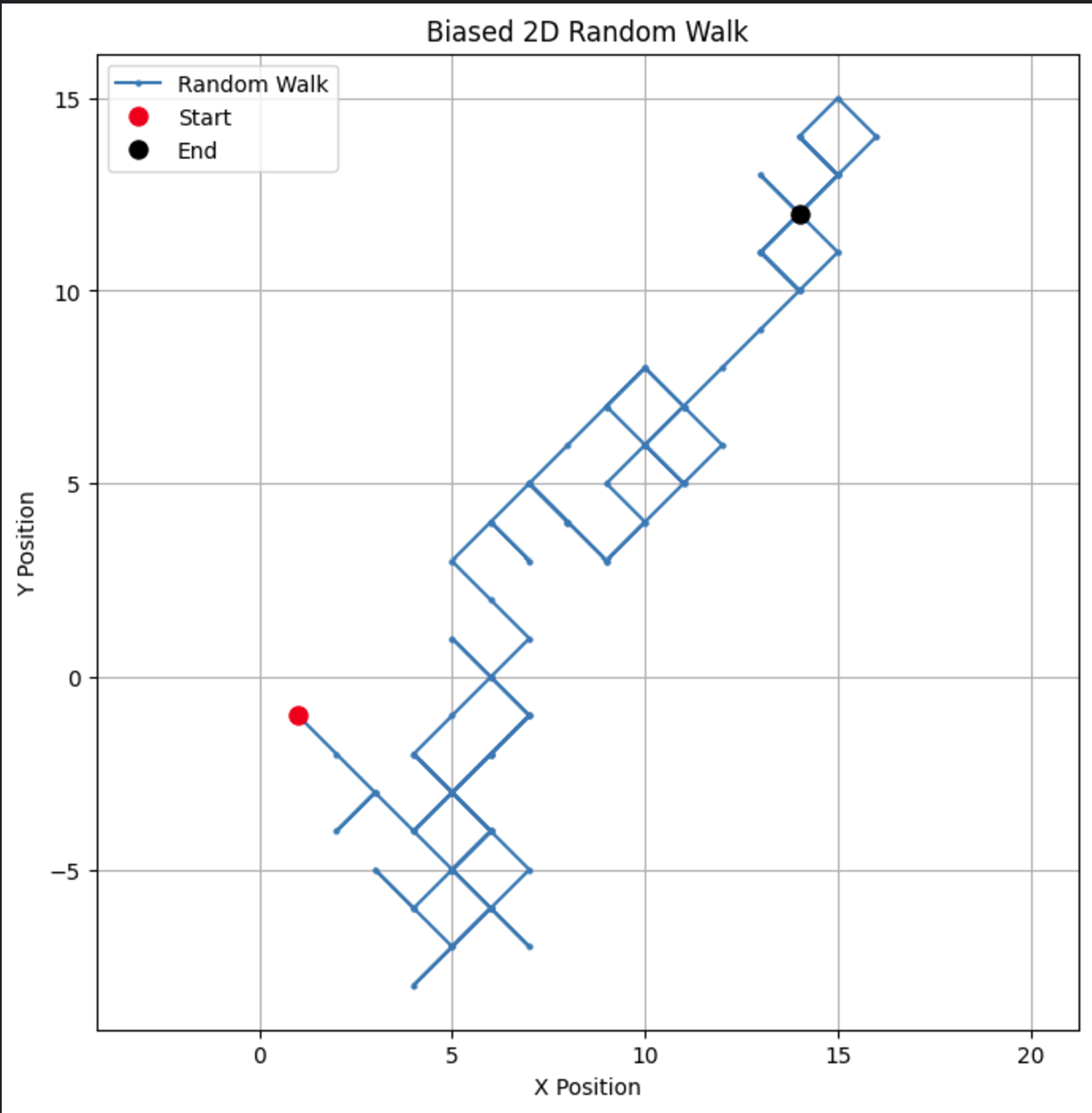
# 參數
n_steps = 100
bias = 0.7  # 步驟+1的概率

# 在x和y方向生成有偏向性的隨機步驟
x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])
y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])

# 計算位置
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# 繪製有偏向性的二維隨機運動
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # 開始的紅點
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # 結束的黑點
plt.title("Biased 2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # 確保兩個軸的比例尺相等
plt.legend()
plt.show()

通過改變偏差，您可以觀察步行如何偏向特定方向，模擬股價漂移或動物遷徙等真實情況。

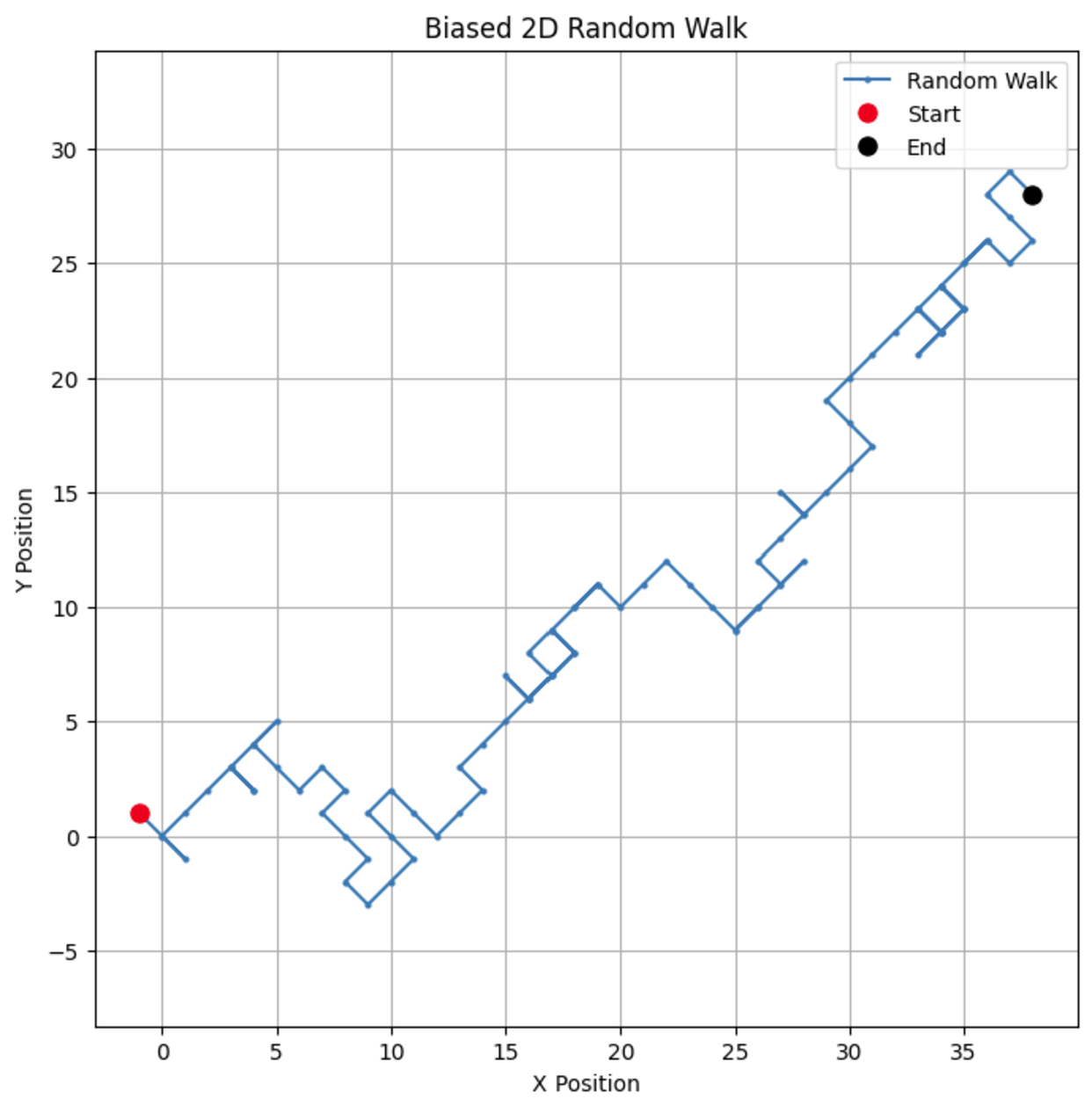
如果我們將偏差參數更改為0.55，可以看到模型行為有顯著不同。儘管它仍然偏向上升，但偏差不那麼強烈，導致更多的迴圈和繞路。

結論

隨機行走是數據科學家的寶貴建模工具，在物理學到金融等領域都有應用。它們模擬複雜的隨機過程的能力使其在許多真實情況下不可或缺。

渴望更多嗎？查看 DataCamp 的概率和统计课程套件。你将找到各种出色的课程，涵盖 Python 和 R 两大主流语言。如果你对更高级内容感兴趣，可以参考 DataCamp 的 Python 统计模拟 课程以及 机器学习入门 教程。或者，如果你准备测试自己的知识，尝试解决这些 概率谜题。