大学で最初のプログラミングベースの統計学の授業で、先生が提案した問題は次のとおりです:水の入った皿の中の単一の花粉粒子のブラウン運動をどのようにモデル化できるでしょうか?何度かの誤った試みの後、私の同級生と私はついに正しい答えであるランダムウォークに辿り着きました。後にこの単純なモデルが、動物の移動から株価の変動までさまざまなものをモデル化するために使用されることを学びました。
この記事では、ランダムウォークの数学的基礎を探求し、異なる種類を調査し、その応用について議論します。ランダムウォークを興味深いものにしている要素の一部は、それがさまざまな分野で使用されていることです。私の例に加えて、物理学では粒子の移動を記述するのに役立ち、金融では株価の変動をモデル化し、生物学では動物の移動パターンを説明します。ランダムウォークは現実世界のランダム性を捉え、確率過程をシミュレートするために重要です。
ランダムウォーク理論の基盤となる統計学をしっかりと学びたい方には、Rでの統計入門コースまたはPythonでの統計入門コースから始めることをお勧めします。
ランダムウォークとは何か?
確率論では、ランダムウォークはパスを構成する一連のランダムなステップを記述するモデルです。言い換えると、ランダムウォークは、独立して特定の確率で決定される一連のステップによって形成されるパスを記述する数学モデルです。この確率性により、ランダムウォークは予測不可能な性質を持ちます。
各瞬間にランダムな方向に一歩ずつ踏み出す人物を想像してみてください。時間の経過とともに、その人物の道は予測不可能で蛇行したものとなります。この概念はシンプルですが、驚くほどの深さと柔軟性を持ち、ランダム性を含むさまざまな実世界のシナリオをモデル化します。
ランダムウォークの概念的な説明。画像はnapkin.ai提供。
ランダムウォークのアイデアは初期の確率研究にさかのぼります。最も古い例の1つである酔っ払いの歩きと呼ばれることが多いものは、ランダムに歩く人が目的地に予測可能に進むのではなく、乱雑にさまよう様子を示しています。このランダム性と、各ステップが前のステップとは独立しているという仮定が、現代のランダムウォークモデルの基礎を築きました。
ランダムウォークの数学の理解
ランダムウォークを理解するために、まず簡単なケース、つまり1次元(1D)のランダムウォークから始めましょう。数直線上の粒子を想像してください。各ステップで数直線上を+1または-1移動することができます。各移動は右に進むか左に進むかが等しい確率で決まります。時間の経過とともに、粒子の位置は広がる確率分布を形成し、それぞれの場所で見つける可能性を表します。
この原則は2次元や3次元にも拡張できます。2次元のランダムウォークでは、粒子は平面上を移動し、上下左右の4つの主要方向のいずれかに等しい確率で移動します。同様に、3次元のランダムウォークでは、粒子は空間内を移動し、上下左右前後の6つの方向のいずれかに等しい確率で移動します。これらの高次元のランダムウォークは、より複雑かつ現実的なシナリオを捉えます。
ランダムウォークの特徴の1つは、その確率的な性質であり、各ステップが現在の位置のみに依存し、過去のステップには依存しません。これにより、ランダムウォークはマルコフ過程の一種となります。マルコフ過程は、将来の状態が現在の状態のみに依存し、それ以前のイベントの系列には依存しない数学的概念です。この「記憶を持たない」移動と、潜在的な位置を記述する確率分布を組み合わせることで、ランダムウォークを理解するための堅固な数学的基盤が提供されます。
ランダムウォークを解析することで、その時間経過における振る舞いを理解するための統計的性質を考察できます。これには、出発地点からの予想される距離、可能な位置の確率分布、原点に戻る確率などの側面を調査することが含まれます。これらの分析は、ランダム性と予測可能性を定量化し、パターンを洞察し、予測を行うのに役立ちます。
ランダムウォークの主な特性
ランダムウォークには、その振る舞いや応用を理解するのに役立ついくつかの重要な特性があります。以下に考慮すべき主な側面を示します:
期待値と分散
一次元のランダムウォークでは、時間の経過とともに出発点からの期待される距離(または平均位置)を計算できます。各ステップが左に移動するか右に移動するかの等しい確率を持つ場合、多くのステップ後の期待位置はゼロのままになります。つまり、平均的には歩行者が出発点の近くにとどまることを意味します。
ただし、位置の分散は、可能な位置の拡がりや分散を測定するもので、各段階で増加します。具体的には、対称ランダムウォークでは、分散が段階の数とともに線形に増加し、時間経過とともに原点からの典型的な距離を示す有用な指標となります。
自己相関
単純なランダムウォークでは段階間に相関はありません(各段階は直前とは独立しています)、しかし、特定のタイプのランダムウォークでは、過去の段階が将来の段階に影響を与える自己相関が導入されることがあります。たとえば、バイアスのあるランダムウォークでは、段階がわずかにある方向に傾向しているため、位置がより予測可能になります。
ランダムウォークにおける自己相関は、ウォークの進行をモデル化および予測する方法に影響を与えます。これは、過去の行動が将来の段階に影響を与えるような、特定の金融モデルなどで特に重要です。
中心極限定理
中心極限定理(CLT)は、多数の独立したランダム変数の和が、元の分布に関係なく正規(またはガウス)分布に従う傾向があることを示しています。ランダムウォークの文脈では、ステップ数が増加するに従い、位置の分布が正規分布に似てくるという意味です。これは、歩行者が出発点から一定の距離にいる確率を近似することができるという有用な特性です。
大数の法則
大数の法則(LLN)は、試行回数やステップ数が増加するにつれて、結果の平均が真の平均に収束することを説明しています。ランダムウォークの場合、平均位置はゼロのままですが、分散と可能な位置の範囲は各追加ステップごとに予測可能に増加します。この原則は、純粋なランダム性と大規模サンプルの中での予測可能な統計的パターンとの間のギャップを埋めるのに役立ちます。
ランダムウォークの種類
ランダムウォークは、各ステップを制御するルールによって大きく異なります。これらのタイプはウォークの振る舞いに影響を与えます。一部は単純な環境や構造化された環境向けに設計されていますが、他のものはより複雑な実世界の現象に適しています。最も一般的なランダムウォークのいくつかを探ってみましょう。
1次元、2次元、3次元のランダムウォーク
ランダムウォークの次元は、その振る舞いにおいて基本的な役割を果たします。1次元のランダムウォークでは、各ステップが直進または後退のどちらかとなります。これにより、このランダムウォークは比較的モデル化しやすく予測しやすいです。
ただし、2次元(平面)および3次元(空間)のランダムウォークに移行すると、可能な経路が大幅に増加し、新しい振る舞いが導入されます。例えば、2次元のランダムウォークでは、出発点に戻る確率が高いのに対し、3次元のランダムウォークでは、この確率が低下します。
この変化は、物理学や化学のような分野で重要であり、粒子が次元の制約に応じて異なる拡散をする可能性があります。
格子ランダムウォーク
格子ランダムウォークでは、移動がグリッドや格子上の離散した点に制限されます。このタイプのウォークは物理学やネットワーク理論で一般的に使用され、ノードがグリッド上に配置され、移動が隣接ノードにのみ発生する場合があります。
一般的な例は2次元格子で、各ステップで直交座標グリッド上の隣接点に移動が可能です。この制約により、移動経路が限定されるため、複雑なネットワークや分子構造のシミュレーション時に便利です。
ガウスランダムウォーク
ガウスランダムウォークでは、各ステップのサイズはガウス(または正規)分布によって決定されます。固定距離での移動ではなく、ステップのサイズはベルカーブ分布に従い、ほとんどのステップが小さく、時折大きなジャンプをします。この種のウォークは、資産価格の変動性を考慮するために金融モデリングで頻繁に使用されます。
異質で偏ったランダムウォーク
異質で偏ったランダムウォークは、一定の確率に基づいてステップの方向とサイズに変動を許します。この柔軟性により、実世界のシナリオにより適応することができます。
異質なランダムウォークでは、任意の方向に移動する確率が位置や外部条件に基づいて変化する可能性があります。例えば、餌を探す動物は既知の資源があるエリアを好むかもしれず、これにより偏ったランダムウォークが生じます。これらのウォークは、文脈依存の行動を研究するのに役立ちます。
ドリフトのあるランダムウォーク
ドリフト付きランダムウォークでは、一定の傾向が一方向に移動する傾向があります。たとえば、株価は日々の変動があるものの、時間と共に全体的に上昇傾向を示すことがあります。これらのウォークにおけるドリフトは、経路に影響を与える外部の力やトレンドを表します。このタイプは、しばしば成長や減少を表すドリフト項を組み込んだモデルが金融業界で見られ、資産価格や市場トレンドを予測する際により現実的なアプローチを提供します。
これらのタイプのランダムウォークは、ランダムでありながら構造化された振る舞いをモデル化するさまざまな方法を提供し、次元の制約、ステップの分布、およびドリフトやバイアスの存在により、さまざまな分野でデータモデリングやシミュレーションに非常に柔軟に適用できます。
ランダムウォークの現実世界への応用
ランダムウォークは理論的な構築物に留まらず、さまざまな分野で実践的な応用において重要な役割を果たしています。ランダムウォークがどのように異なるセクターで現実世界の問題解決に貢献しているかを探ってみましょう。
データサイエンスや機械学習における応用
コンピュータサイエンス
ランダムウォークは、ランダムサンプリング、ウェブグラフトラバーサル、および画像セグメンテーションなど、いくつかのコンピュータサイエンスアルゴリズムの基盤となっています。たとえば、GoogleのPageRankアルゴリズムは、関連性に基づいてウェブページのランキングをランダムウォークを使用して行いました、ユーザーがインターネット上のリンク間をランダムに移動する方法をシミュレートしています。
特徴抽出
機械学習では、ランダムウォークを使用してデータポイント内の関係を強調することで、特徴を抽出するのに役立ちます。たとえば、ネットワーク分析では、ランダムウォークを使用してクラスターやコミュニティを明らかにすることができ、推薦システムやソーシャルネットワーク分析などのタスクを支援します。
異常検知
ランダムウォークを使用してデータセット内の異常を検出することもできます。たとえば、ランダムウォークモデルの典型的なパスからデータポイントが大きく逸脱する場合、これらのポイントはデータ内の異常なイベントやエラーを示す可能性があります。異常検知は、特にサイバーセキュリティや詐欺検出などの分野で特に価値があります。
確率過程のシミュレーション
ランダムウォークは、データサイエンティストが予測不可能な現実世界の現象をモデル化するために使用する、確率的またはランダムに決定されるプロセスをシミュレートします。ランダムウォークをシミュレートすることで、天候パターンや顧客の行動など、正確な予測が難しいシステムに対する洞察を得ることができます。
時間系列予測
時間系列分析では、ランダムウォークは、ファイナンスのランダムウォーク仮説を含む、特定の予測モデルの基礎を形成します。これらのモデルは、将来の値が時系列の中で過去の傾向とは関係なく、最も最近の値にのみ依存すると仮定します。時間系列予測について詳しくは、時間系列予測のためのARIMA:完全ガイドをご覧ください。また、Hyndman教授と一緒に取るRでの予測コースでは、ランダムウォークモデルを単純な予測や季節性のある単純な予測手法につなげて説明しています。
他の分野での応用
ファイナンス
ランダムウォークの最も注目すべき用途の1つは、金融モデリングであり、特に株価を予測するために使われます。効率的市場仮説によれば、株価の変動は基本的にランダムであり、新しい情報がすぐに吸収されるため、未来の価格は予測不可能です。ランダムウォークを使って、時間の経過とともに株価の変動をモデル化することができ、価格が予測不可能なパスでどのように変動するかを示すことができます。
数学
純粋数学では、ランダムウォークは複雑な問題の解決策を提供します。例えば、ランダムウォークは、ラプラスの方程式の解決、ネットワークの解析、組合せ論の探索などに役立ちます。
物理学と化学
自然科学では、ランダムウォークは、分子が媒体を通じて広がる過程などの拡散プロセスのモデリングに不可欠です。流体中に浮遊する粒子が周囲の分子との衝突によって予測不可能に移動するブラウン運動は、ランダムウォークを使用して正確にシミュレートできる古典的な例です。実際、私が最初にランダムウォークについて学んだのはこれでした。
生物学
ランダムウォークは、動物の移動パターンを研究するために生態学で貴重です。資源を探している動物は、ランダムウォークのように見えることがあり、時には既知の資源がある地域に偏って移動します。人口や遺伝子の拡散など他の生物学的概念も、しばしばランダムウォークの原理でモデル化され、それによって生態系内の変化を理解し予測することが容易になります。
ランダムウォークの特殊なケースとバリエーション
クラシックなランダムウォークに加え、いくつかの高度なバリエーションがあり、専門的な応用に合わせて概念を拡張しています。
自己回避ウォーク
自己回避ウォークは、通過した位置を再訪しないランダムウォークです。このバリエーションは、重ねられた形でポリマーチェーンが形成される様子をモデル化するなど、ポリマーケミストリーなどの分野で特に有用です。各ステップが以前に訪れたポイントを避けるため、自己回避ウォークは従来のランダムウォークよりも制約が多く、計算上の課題がありますが、閉じた空間内の重ならない経路を理解するのに役立ちます。
分岐
ランダムウォークの分岐では、経路が複数の枝に分かれ、各枝がランダムウォークをたどります。この種のウォークは、細胞分裂や情報のネットワークを通じた拡散などの分岐プロセスのモデリングに重要です。各「枝」は共通の源から発生した独立したランダム経路を表します。
相関ウォーク
相関ウォークは、各ステップの方向が前のステップに一部影響を受けるという概念をさらに進めたものです。このバリアントは、変化がランダムではなく徐々に起こるシステムに慣性をモデリングするのに役立ちます。相関ウォークは、価格トレンドをシミュレートするために金融分野でよく用いられたり、動物が過去の方向を一部記憶しながら環境をどのように航行するかを理解するために動きの生態学で適用されることがよくあります。
ループ除去ウォーク
ループ除去ウォークは、ループまたは自己交差する経路が形成されるとそれらが削除される変種です。ステップが位置を再訪するたびに、介在するループが消去され、簡素化された、繰り返しのない経路が残ります。ループ除去ウォークは、ネットワーク分析や迷路生成アルゴリズムで一般的に使用されており、冗長性を回避する経路を作成します。
Python でランダムウォークを実装する
Python でランダムウォークを実装してみましょう。始める前に、Python(Python 3.10 を使用します)がインストールされていることと、必要なライブラリが利用可能であることを確認してください。不足しているライブラリは pip を使用してインストールできます。以下を使用します:
import numpy as np # 数値演算とランダムなステップの生成用 import matplotlib.pyplot as plt # ランダムウォークのプロットと可視化用
1次元ランダムウォーク
まずは、各ステップがランダムに選択された +1 または -1 の単純な一次元ランダムウォークから始めましょう。
# パラメータ n_steps = 100 # ステップ数 # ランダムなステップの生成: +1 または -1 steps = np.random.choice([-1, 1], size=n_steps) # 位置の計算 positions = np.cumsum(steps) # ランダムウォークのプロット plt.figure(figsize=(10, 6)) plt.plot(positions, marker='o', linestyle='-', markersize=4) plt.title("1D Random Walk") plt.xlabel("Step") plt.ylabel("Position") plt.grid(True) plt.show()
これは単純なランダムウォークを生成し、時間の経過を視覚化します。このコードを実行すると、次のような出力が得られます:
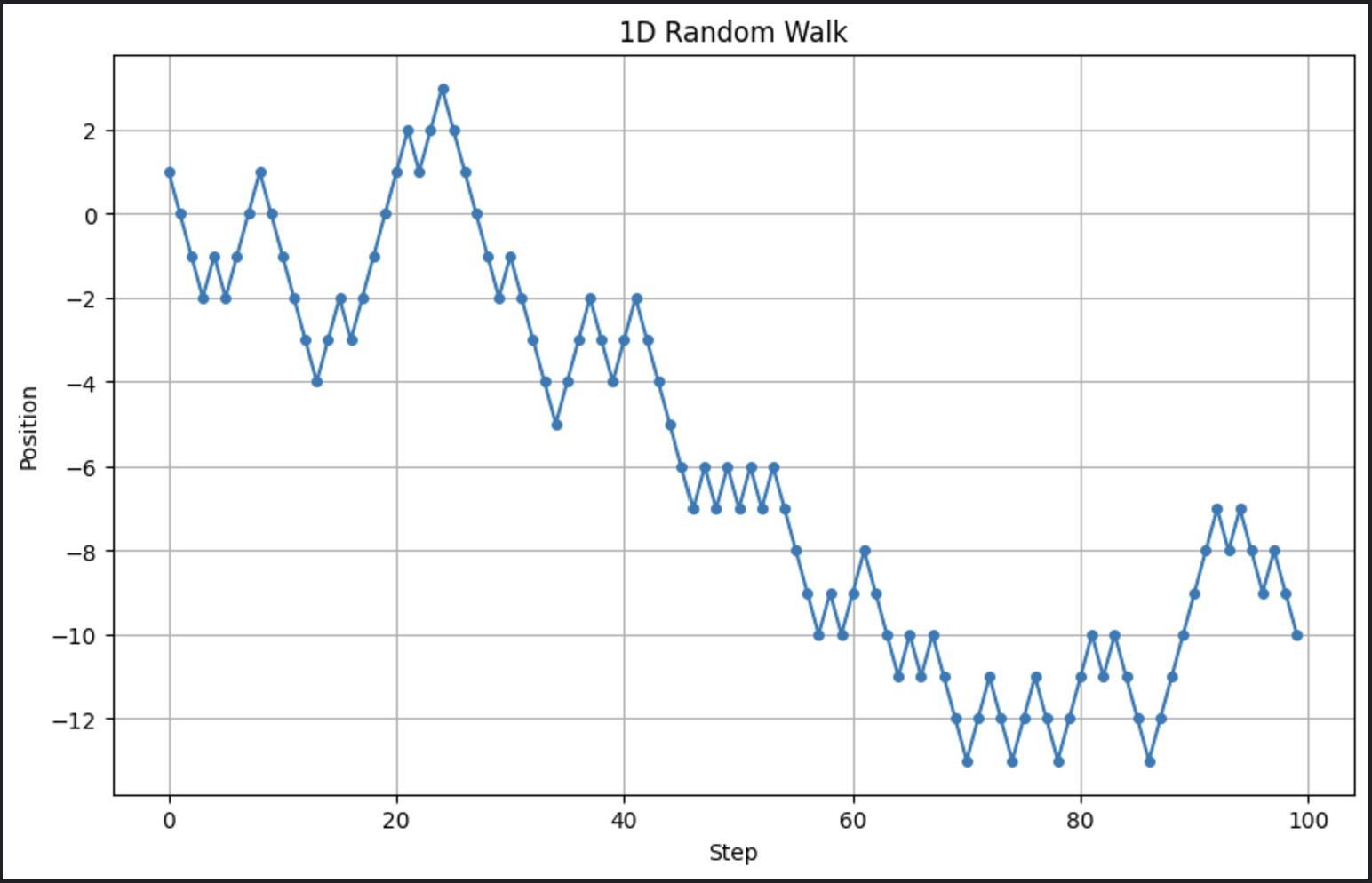
ここで覚えておいてください、私たちは確率モデルを実行しています。つまり、実行するたびに出力は少し異なる見え方をします。
2Dランダムウォーク
さて、ランダムウォークを2次元に拡張しましょう。各ステップで方向はランダムに選択されます。
# パラメータ n_steps = 500 # x方向とy方向のランダムなステップを生成 x_steps = np.random.choice([-1, 1], size=n_steps) y_steps = np.random.choice([-1, 1], size=n_steps) # 位置を計算 x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # 2Dランダムウォークをプロット plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # 開始地点の赤い点 plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # 終了地点の黒い点 plt.title("2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # 両軸のスケーリングを均等にする plt.legend() plt.show()
このコードは、2次元で視覚的に魅力的なパスを作成します。
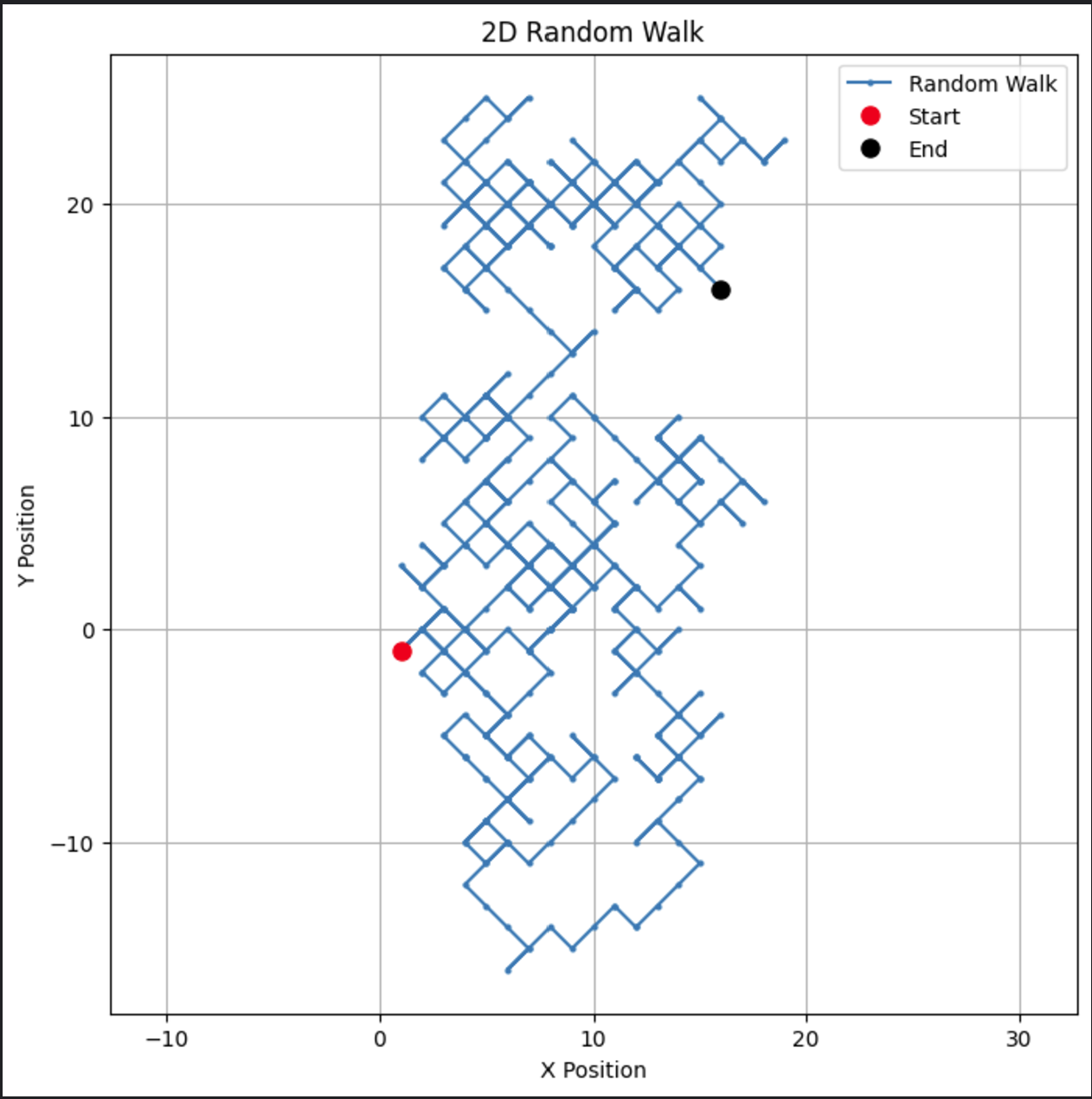
この種の2次元ランダムウォークは、粒子の動きや空間モデリングなどのアプリケーションに適応させることができます。
バイアス付きランダムウォーク
最後に、もう少し複雑な例を見てみましょう:バイアス付きランダムウォーク。バイアスを導入するために、各ステップの方向の確率を調整することができます。たとえば、上向きのステップをより可能性が高くすることができます。
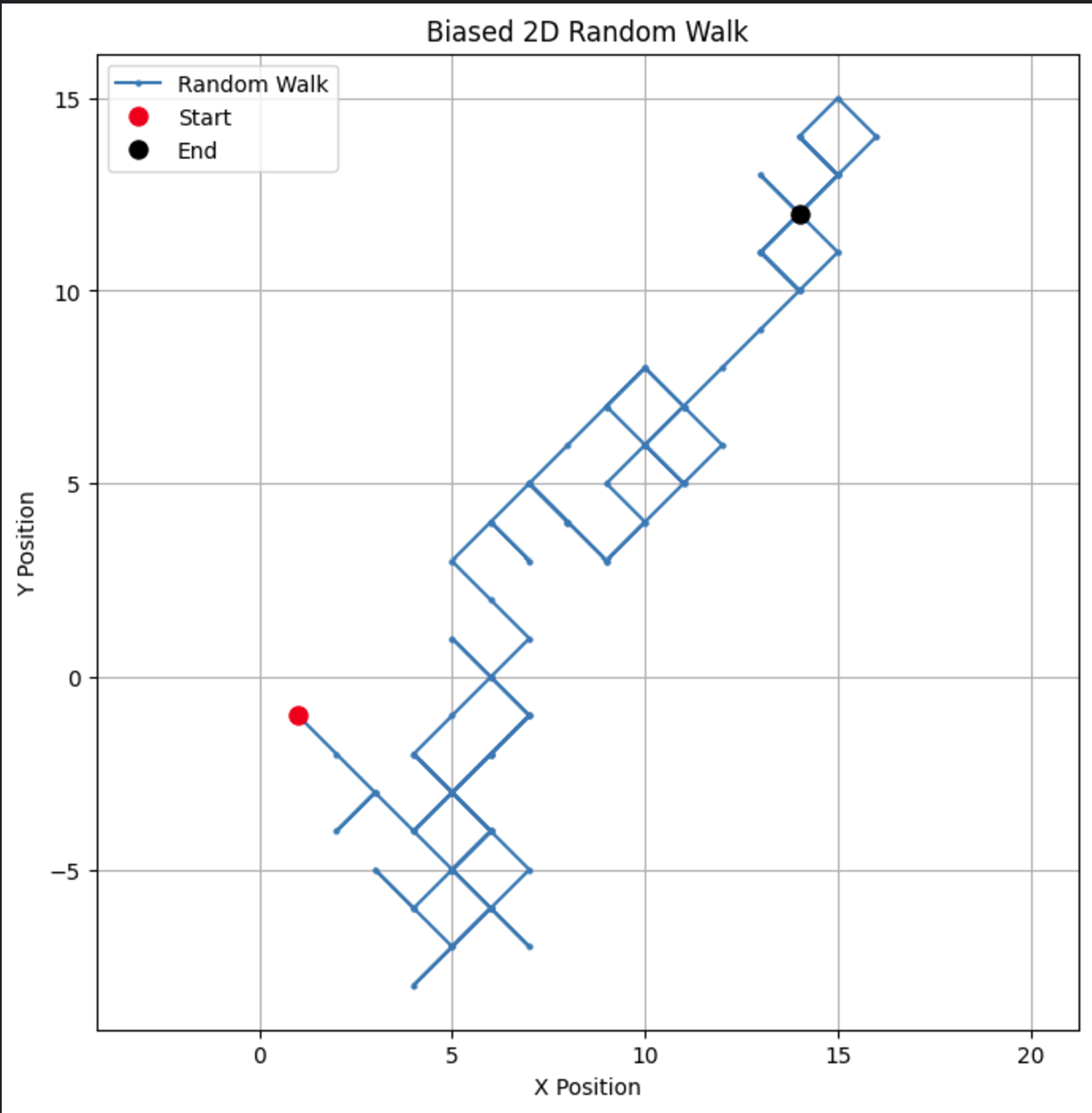
# パラメータ n_steps = 100 bias = 0.7 # +1 ステップの確率 # xおよびy方向のバイアス付きランダムステップを生成 x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) # 位置を計算 x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # バイアス付き2Dランダムウォークをプロット plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # 開始地点の赤い点 plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # 終了地点の黒い点 plt.title("Biased 2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # 両軸の等しいスケーリングを確認 plt.legend() plt.show()
バイアスを変更することで、ウォークが特定の方向を好む傾向がどのようになるかを観察でき、株価のドリフトや動物の移動パターンなどの現実世界のシナリオをシミュレートできます。
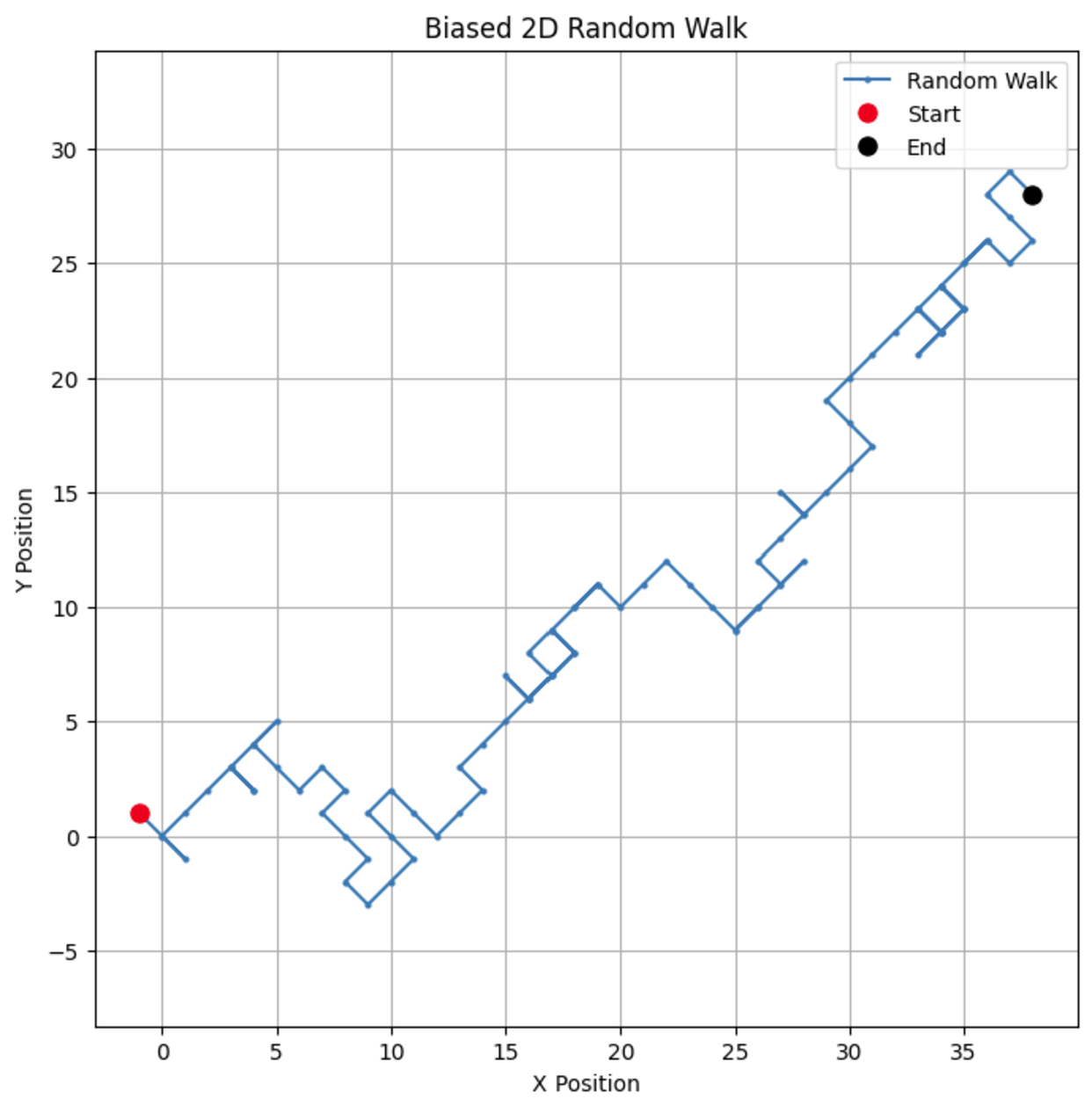
バイアスパラメータを0.55に変更すると、モデルの振る舞いが劇的に異なることがわかります。上昇する方向にバイアスがありますが、それほど強くないため、より多くのループや遠回りが生じます。
結論
ランダムウォークは、物理学から金融などさまざまな分野でデータサイエンティストにとって貴重なモデリングツールです。複雑な確率過程をモデル化する能力は、多くの現実世界のシナリオで不可欠です。
もっと知りたいですか? DataCampの確率と統計のコース群 をチェックしてみてください。PythonとRの両方でさまざまな優れたコースを見つけることができます。より高度な内容に興味がある場合は、DataCampの Pythonにおける統計的シミュレーション コースや 機械学習入門 チュートリアルをチェックしてみてください。知識を試したい場合は、これらの 確率パズル に取り組んでみてください。













