Nel mio primo corso di statistica basato sulla programmazione all’università, il mio insegnante propose una domanda: come possiamo modellare il moto browniano di una singola particella di polline in una bacinella d’acqua? Dopo diversi tentativi errati, i miei compagni di classe ed io alla fine ci imbattemmo nella risposta corretta: una passeggiata casuale. Ho poi scoperto che questo semplice modello viene utilizzato per modellare ogni sorta di cose, dai movimenti degli animali alle fluttuazioni dei prezzi delle azioni.
In questo articolo, esploreremo le basi matematiche delle passeggiate casuali, esamineremo i diversi tipi e discuteremo le loro applicazioni. Parte di ciò che rende interessante la passeggiata casuale è che viene utilizzata in così tante discipline diverse. Oltre al mio esempio, in fisica aiuta a descrivere il movimento delle particelle; in finanza, modella le fluttuazioni dei prezzi delle azioni; e in biologia, spiega i modelli di movimento degli animali. Le passeggiate casuali catturano la casualità del mondo reale, che è fondamentale per simulare processi stocastici.
Per coloro che cercano di costruire una solida base nelle statistiche che sottendono la teoria del cammino casuale, raccomandiamo di iniziare con il corso Introduzione alle Statistiche in R o il corso Introduzione alle Statistiche in Python.
Cosa Sono i Cammini Casuali?
In teoria della probabilità, un cammino casuale è un modello che descrive una sequenza di passi casuali che compongono un percorso. Oppure, potremmo dire che un cammino casuale è un modello matematico che descrive un percorso formato da una sequenza di passi, ciascuno determinato in modo indipendente e con una certa probabilità. Questa stocasticità rende i cammini casuali intrinsecamente imprevedibili.
Immagina una persona che compie un passo in una direzione casuale ad ogni momento. Col passare del tempo, il loro percorso forma un sentiero imprevedibile e tortuoso. Nonostante la sua semplicità, questo concetto ha una sorprendente profondità e versatilità, modellando vari scenari del mondo reale che coinvolgono la casualità.
Una spiegazione concettuale di un cammino casuale. Immagine gentilmente fornita da napkin.ai.
L’idea dei cammini casuali risale ai primi studi sulla probabilità. Uno dei primi esempi, spesso chiamato il cammino del ubriaco, illustra come una persona che si muove casualmente vagherà in modo erratico piuttosto che muoversi in modo prevedibile verso una destinazione. Questa casualità, combinata con l’assunzione che ogni passo è indipendente dai precedenti, ha posto le basi per i moderni modelli di cammino casuale.
Comprendere la Matematica dei Cammini Casuali
Per comprendere i cammini casuali, iniziamo con un caso semplice: un cammino casuale monodimensionale (1D).Immagina una particella su una retta numerica. Può muoversi di +1 o -1 lungo la retta numerica ad ogni passo. Ogni movimento è determinato da una probabilità uguale di muoversi a destra o a sinistra. Nel tempo, la posizione della particella forma una distribuzione di probabilità che si espande, rappresentando la probabilità di trovarla in varie posizioni.
Questo principio può essere esteso a due o tre dimensioni. In un cammino casuale bidimensionale (2D), la particella si muove su un piano e può spostarsi in una delle quattro direzioni cardinali (su, giù, sinistra, destra) con probabilità uguale. Allo stesso modo, in un cammino casuale tridimensionale (3D), la particella si muove nello spazio e può spostarsi in una delle sei direzioni possibili (su, giù, sinistra, destra, avanti, indietro) con probabilità uguale. Questi cammini casuali in dimensioni superiori catturano scenari ancora più complessi e realistici.
Una caratteristica definente dei cammini casuali è la loro natura stocastica, il che significa che ogni passo dipende solo dalla posizione attuale e non dai passi precedenti. Questo li rende un tipo di processo di Markov—un concetto matematico in cui lo stato futuro dipende esclusivamente dallo stato presente, non dalla sequenza di eventi che lo hanno preceduto. Questo movimento “senza memoria”, combinato con distribuzioni di probabilità che descrivono posizioni potenziali, fornisce una solida base matematica per comprendere i cammini casuali.
Possiamo analizzare una camminata casuale utilizzando proprietà statistiche per comprendere il suo comportamento nel tempo. Ciò implica esaminare aspetti come la distanza attesa dal punto di partenza, la distribuzione di probabilità delle posizioni possibili e la probabilità di tornare all’origine. Queste analisi ci aiutano a quantificare la casualità e la prevedibilità, fornendo intuizioni sui modelli e facendo previsioni.
Proprietà Chiave delle Camminate Casuali
Le camminate casuali hanno diverse proprietà importanti che ci aiutano a comprendere il loro comportamento e le applicazioni. Ecco alcuni aspetti chiave da considerare:
Aspettativa e varianza
In una camminata casuale unidimensionale, possiamo calcolare la distanza attesa (o posizione media) dal punto di partenza nel tempo. Se ogni passo ha un’uguale probabilità di muoversi a sinistra o a destra, la posizione attesa dopo molti passi rimane zero, implicando che, in media, il camminatore rimane vicino al punto di partenza.
Tuttavia, la varianza della posizione, che misura la dispersione o la diffusione delle posizioni possibili, aumenta ad ogni passo. Specificamente, in un passeggiata casuale simmetrica, la varianza cresce linearmente con il numero di passi, rendendola un indicatore utile della distanza tipica dall’origine nel tempo.
Autocorrelazione
Mentre le passeggiate casuali semplici non hanno correlazione tra i passi (ogni passo è indipendente dall’ultimo), certi tipi di passeggiate casuali introducono autocorrelazione, dove i passi passati possono influenzare i futuri. Ad esempio, in una passeggiata casuale sbilanciata, i passi possono avere una leggera tendenza in una direzione, rendendo le posizioni più prevedibili.
L’autocorrelazione in una passeggiata casuale influisce su come modelli e prevedi il progresso della passeggiata. Questo è particolarmente rilevante in applicazioni dove il comportamento passato influenza i passi futuri, come in certi modelli finanziari.
Teorema del limite centrale
Il teorema del limite centrale (TLC) ci dice che la somma di un gran numero di variabili casuali indipendenti tende a seguire una distribuzione normale (o gaussiana), indipendentemente dalla distribuzione originale. Nel contesto delle passeggiate casuali, questo significa che man mano che il numero di passi aumenta, la distribuzione delle posizioni tende a somigliare a una distribuzione normale. Questa è una proprietà utile perché ci consente di approssimare la probabilità di trovare il camminatore a certe distanze dal punto di partenza.
Legge dei grandi numeri
La legge dei grandi numeri (LGN) spiega che man mano che il numero di prove o passi aumenta, la media dei risultati converge alla vera media. Per le passeggiate casuali, questo significa che mentre la posizione media rimane zero, la varianza e l’intervallo delle posizioni possibili crescono in modo prevedibile ad ogni passo aggiuntivo. Questo principio aiuta a colmare il divario tra pura casualità e schemi statistici prevedibili in grandi campioni.
Tipi di passeggiate casuali
I cammini casuali variano ampiamente a seconda delle regole che governano ciascun passo. Questi tipi influenzano il comportamento del cammino. Alcuni sono progettati per ambienti semplici o strutturati, mentre altri sono attrezzati per fenomeni del mondo reale più complessi. Esploriamo alcuni dei tipi più comuni di cammini casuali.
Cammini casuali 1D, 2D e 3D
La dimensionalità di un cammino casuale gioca un ruolo fondamentale nel suo comportamento. In un cammino casuale 1D, ogni passo è o un movimento in avanti o un movimento all’indietro lungo una linea. Questo rende il cammino relativamente facile da modellare e prevedere.
Tuttavia, man mano che ci spostiamo verso cammini 2D (piano) e 3D (spazio), i percorsi possibili aumentano significativamente, introducendo nuovi comportamenti. Ad esempio, in un cammino casuale 2D, la probabilità di tornare al punto di partenza rimane alta, mentre in un cammino casuale 3D, questa probabilità diminuisce.
Questa modifica è importante in campi come la fisica e la chimica, dove le particelle possono diffondere in modo diverso a seconda dei vincoli dimensionali.
Camminata casuale su reticolo
In una camminata casuale su reticolo, il movimento è confinato a punti discreti su una griglia o reticolo. Questo tipo di camminata è comunemente usato in fisica e teoria delle reti, dove i nodi sono disposti in una griglia, e il movimento può avvenire solo verso nodi adiacenti.
Un esempio comune è un reticolo 2D, dove ogni passo consente il movimento verso punti adiacenti su una griglia cartesiana. Questo vincolo semplifica la modellazione limitando i percorsi di movimento, il che è utile quando si simulano reti complesse o strutture molecolari.
Camminata casuale gaussiana
In una passeggiata casuale gaussiana, la dimensione di ciascun passo è determinata da una distribuzione gaussiana (o normale). Invece di muoversi a una distanza fissa, la dimensione del passo varia in base a una distribuzione a campana, con la maggior parte dei passi piccoli e occasionali salti più grandi. Questo tipo di passeggiata è frequentemente utilizzato nella modellazione finanziaria per tenere conto della variabilità nei cambiamenti dei prezzi degli attivi.
Passeggiate casuali eterogenee e biased
Le passeggiate casuali eterogenee e biased consentono variazioni nella direzione e nella dimensione del passo in base a determinate probabilità. Questa flessibilità le rende più adattabili a scenari del mondo reale.
In una passeggiata casuale eterogenea, la probabilità di muoversi in qualsiasi direzione può cambiare in base alla posizione o alle condizioni esterne. Ad esempio, gli animali che cercano cibo possono favorire aree con risorse note, creando una passeggiata casuale biased. Queste passeggiate sono utili per studiare comportamenti che dipendono da fattori contestuali.
Passeggiata casuale con deriva
In un passeggiata casuale con deriva, c’è una tendenza costante a muoversi in una direzione. Ad esempio, i prezzi delle azioni possono mostrare una tendenza generale al rialzo nel tempo nonostante le fluttuazioni quotidiane. La deriva in queste passeggiate rappresenta una forza esterna o una tendenza che influenza il percorso. Questo tipo è spesso visto in finanza, dove i modelli incorporano un termine di deriva per rappresentare crescita o declino, fornendo un approccio più realistico alla previsione dei prezzi degli asset e delle tendenze di mercato.
Ognuno di questi tipi di passeggiata casuale ha uno scopo unico, offrendo diversi modi per modellare comportamenti casuali, ma strutturati. I vincoli dimensionali, la distribuzione dei passi e la presenza di deriva o bias rendono le passeggiate casuali altamente versatili per la modellazione e la simulazione dei dati in vari campi.
Applicazioni nel Mondo Reale delle Passeggiate Casuali
Le passeggiate casuali sono più di semplici costrutti teorici; svolgono un ruolo essenziale in molte applicazioni pratiche in diverse discipline. Esploriamo come le passeggiate casuali informano la risoluzione di problemi nel mondo reale in vari settori.
Applicazioni nella scienza dei dati e nell’apprendimento automatico
Informatica
I percorsi casuali sono alla base di diversi algoritmi di informatica, come il campionamento casuale, la traversata dei grafi web e la segmentazione delle immagini. Ad esempio, l’algoritmo PageRank di Google utilizza percorsi casuali per classificare le pagine web in base alla loro rilevanza, simulando come un utente potrebbe navigare casualmente tra i link su Internet.
Estrazione delle caratteristiche
Nell’apprendimento automatico, i percorsi casuali possono aiutare a estrarre caratteristiche evidenziando le relazioni tra i punti dati. Ad esempio, nell’analisi delle reti, i percorsi casuali possono rivelare cluster o comunità, assistendo in compiti come i sistemi di raccomandazione e l’analisi delle reti sociali.
Rilevamento delle anomalie
I percorsi casuali possono essere utilizzati anche per rilevare anomalie nei dataset. Ad esempio, se i punti dati deviano in modo significativo da un percorso tipico in un modello di percorso casuale, questi punti potrebbero indicare eventi insoliti o errori nei dati. Il rilevamento delle anomalie è particolarmente prezioso in campi come la cybersecurity e la rilevazione delle frodi.
Simulazione di processi stocastici
I cammini casuali simulano processi stocastici, o determinati casualmente, consentendo agli scienziati dei dati di modellare fenomeni imprevedibili del mondo reale. Simulando cammini casuali, possiamo ottenere intuizioni su sistemi in cui la previsione precisa è impegnativa, come i modelli meteorologici o il comportamento dei clienti.
Previsione delle serie temporali
Nell’analisi delle serie temporali, i cammini casuali formano la base per alcuni modelli di previsione, inclusa l’ipotesi del cammino casuale in finanza. Questi modelli assumono che i valori futuri in una serie temporale dipendano esclusivamente dall’ultimo valore, senza correlazione con le tendenze passate.Per ulteriori informazioni sulla previsione delle serie temporali, dai un’occhiata a ARIMA per la Previsione delle Serie Temporali: Una Guida Completa. Inoltre, segui il nostro corso Previsione in R con il Professore Hyndman, che collega i modelli di cammino casuale ai metodi di previsione naive e naive stagionali.
Applicazioni in altri campi
Finanza
Uno degli usi più notevoli dei cammini casuali è nella modellizzazione finanziaria, in particolare per prevedere i prezzi delle azioni. L’ipotesi del mercato efficiente suggerisce che i movimenti dei prezzi delle azioni siano essenzialmente casuali, poiché nuove informazioni vengono assorbite istantaneamente, rendendo i prezzi futuri imprevedibili. I cammini casuali possono essere utilizzati per modellare le variazioni dei prezzi delle azioni nel tempo, illustrando come i prezzi fluttuano senza un percorso prevedibile.
Matematica
In matematica pura, i cammini casuali forniscono soluzioni a problemi complessi. Ad esempio, sono utili per risolvere l’equazione di Laplace, analizzare reti ed esplorare combinatoria.
Fisica e chimica
Nelle scienze fisiche, i cammini casuali sono fondamentali per modellare i processi di diffusione, come il modo in cui le molecole si diffondono attraverso un mezzo. Il moto browniano, in cui particelle sospese in un fluido si muovono in modo imprevedibile a causa delle collisioni con molecole circostanti, è un esempio classico che può essere simulato accuratamente utilizzando cammini casuali. Questo è effettivamente come ho imparato per la prima volta sui cammini casuali.
Biologia
I cammini casuali sono preziosi in ecologia per studiare i modelli di movimento degli animali. Gli animali che cercano risorse possono sembrare muoversi in un cammino casuale, talvolta inclinato verso regioni con risorse conosciute. Altri concetti biologici, come la diffusione di popolazioni o geni, possono spesso essere modellati con i principi del cammino casuale, rendendo più facile comprendere e prevedere i cambiamenti all’interno degli ecosistemi.
Casi speciali e varianti dei cammini casuali
Oltre al cammino casuale classico, diverse varianti avanzate estendono il concetto per adattarsi a applicazioni specializzate.
Cammini autoevitanti
Un cammino autoevitante è un cammino casuale in cui il percorso non ritorna mai su nessuna posizione già visitata. Questa variante è particolarmente utile in campi come la chimica dei polimeri, dove può modellare come si formano le catene polimeriche senza attraversarsi. Poiché ogni passo evita punti già visitati, i cammini autoevitanti sono più vincolati rispetto ai cammini casuali tradizionali. Ciò significa che sono computazionalmente impegnativi ma utili per comprendere percorsi non sovrapposti in spazi ristretti.
Diramazione
Nelle camminate casuali ramificate, il percorso può dividersi in più rami, con ogni ramo che segue una camminata casuale. Questo tipo di camminata è fondamentale per modellare processi ramificati come la divisione cellulare o la diffusione di informazioni attraverso le reti. Ogni “ramo” rappresenta un percorso casuale indipendente che origina da una fonte comune.
Camminate correlate
Le camminate correlate portano questo concetto un passo oltre, dove la direzione di ogni passo è parzialmente influenzata dal passo precedente. Questa variante è utile per modellare l’inerzia in sistemi in cui i cambiamenti avvengono gradualmente anziché casualmente. Le camminate correlate sono spesso applicate in finanza per simulare tendenze dei prezzi o in ecologia del movimento per comprendere come gli animali navigano nei loro ambienti con una certa memoria della loro direzione passata.
Camminate senza cicli
Una camminata senza cicli è una variante in cui i cicli, o i percorsi che si incrociano, vengono rimossi man mano che si formano. Ogni volta che un passo visita nuovamente una posizione, il ciclo intermedio viene cancellato, lasciando un percorso snodato e non ripetitivo. Le camminate senza cicli sono comunemente applicate nell’analisi delle reti e negli algoritmi di generazione di labirinti perché creano percorsi che evitano la ridondanza.
Implementazione dei Random Walk in Python
Proviamo a implementare un random walk in Python.Per iniziare, assicurati di avere Python installato (utilizzeremo Python 3.10) e le librerie necessarie disponibili. Puoi installare eventuali librerie mancanti utilizzando pip. Ecco cosa utilizzeremo:
import numpy as np # per operazioni numeriche e generazione di passi casuali import matplotlib.pyplot as plt # per tracciare e visualizzare i random walk
Random walk 1D
Iniziamo con un semplice random walk unidimensionale, dove ogni passo è +1 o -1, scelto casualmente.
# Parametri n_steps = 100 # Numero di passi # Genera passi casuali: +1 o -1 steps = np.random.choice([-1, 1], size=n_steps) # Calcola le posizioni positions = np.cumsum(steps) # Traccia il random walk plt.figure(figsize=(10, 6)) plt.plot(positions, marker='o', linestyle='-', markersize=4) plt.title("1D Random Walk") plt.xlabel("Step") plt.ylabel("Position") plt.grid(True) plt.show()
Questo genera una semplice passeggiata casuale e visualizza la progressione nel tempo. Ecco l’output quando eseguo questo codice:
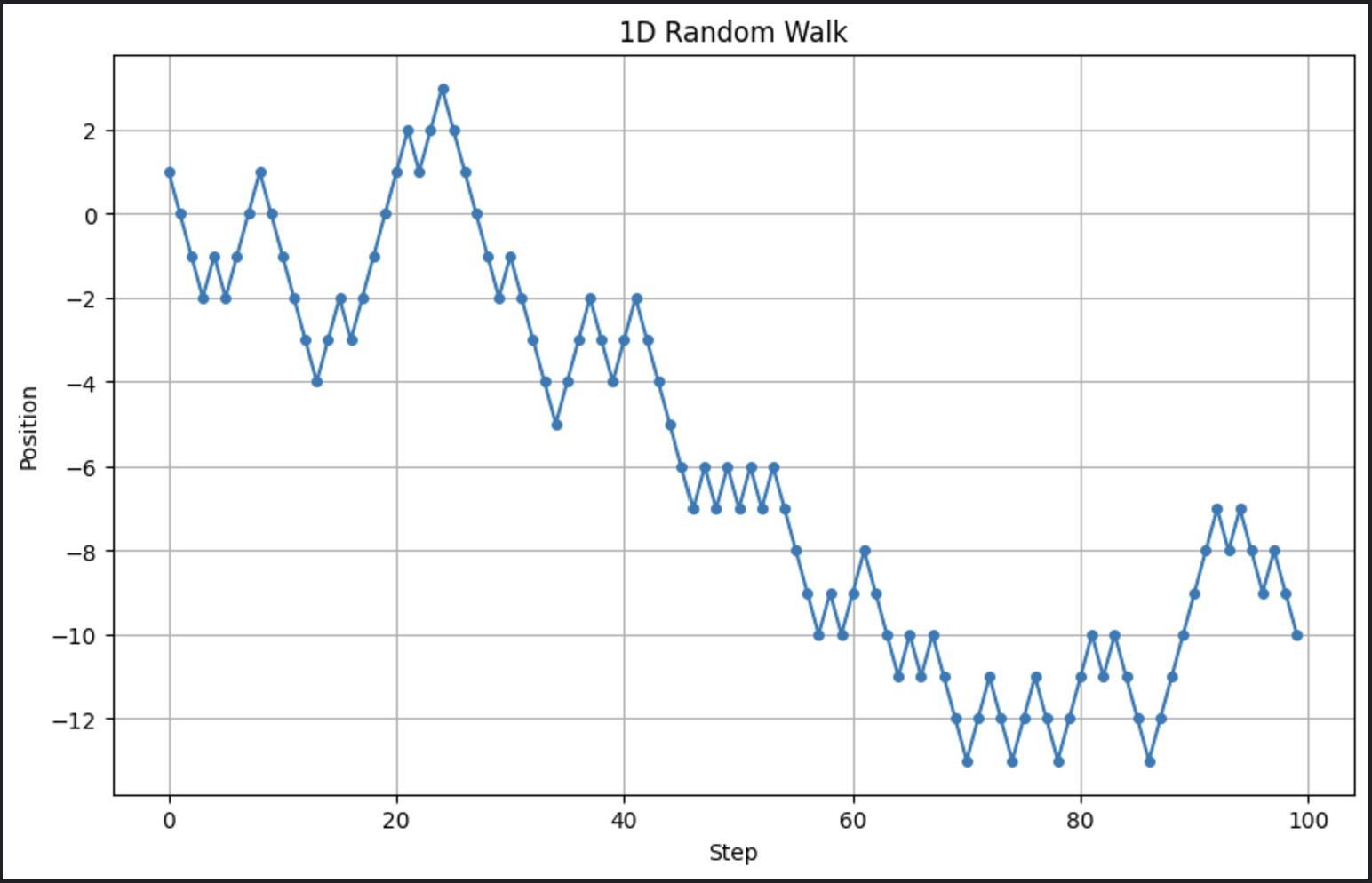
Ora ricorda, stiamo eseguendo un modello stocastico. Questo significa che ogni volta che lo eseguiamo, l’output apparirà un po’ diverso.
Passeggiata casuale 2D
Ora estendiamo la passeggiata casuale a due dimensioni. Ad ogni passo, la direzione sarà scelta casualmente.
# Parametri n_steps = 500 # Genera passi casuali nelle direzioni x e y x_steps = np.random.choice([-1, 1], size=n_steps) y_steps = np.random.choice([-1, 1], size=n_steps) # Calcola le posizioni x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Traccia la passeggiata casuale 2D plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Punto rosso per l'inizio plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Punto nero per la fine plt.title("2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Garantisce una scala uguale per entrambi gli assi plt.legend() plt.show()
Questo codice crea un percorso visivamente coinvolgente in due dimensioni.
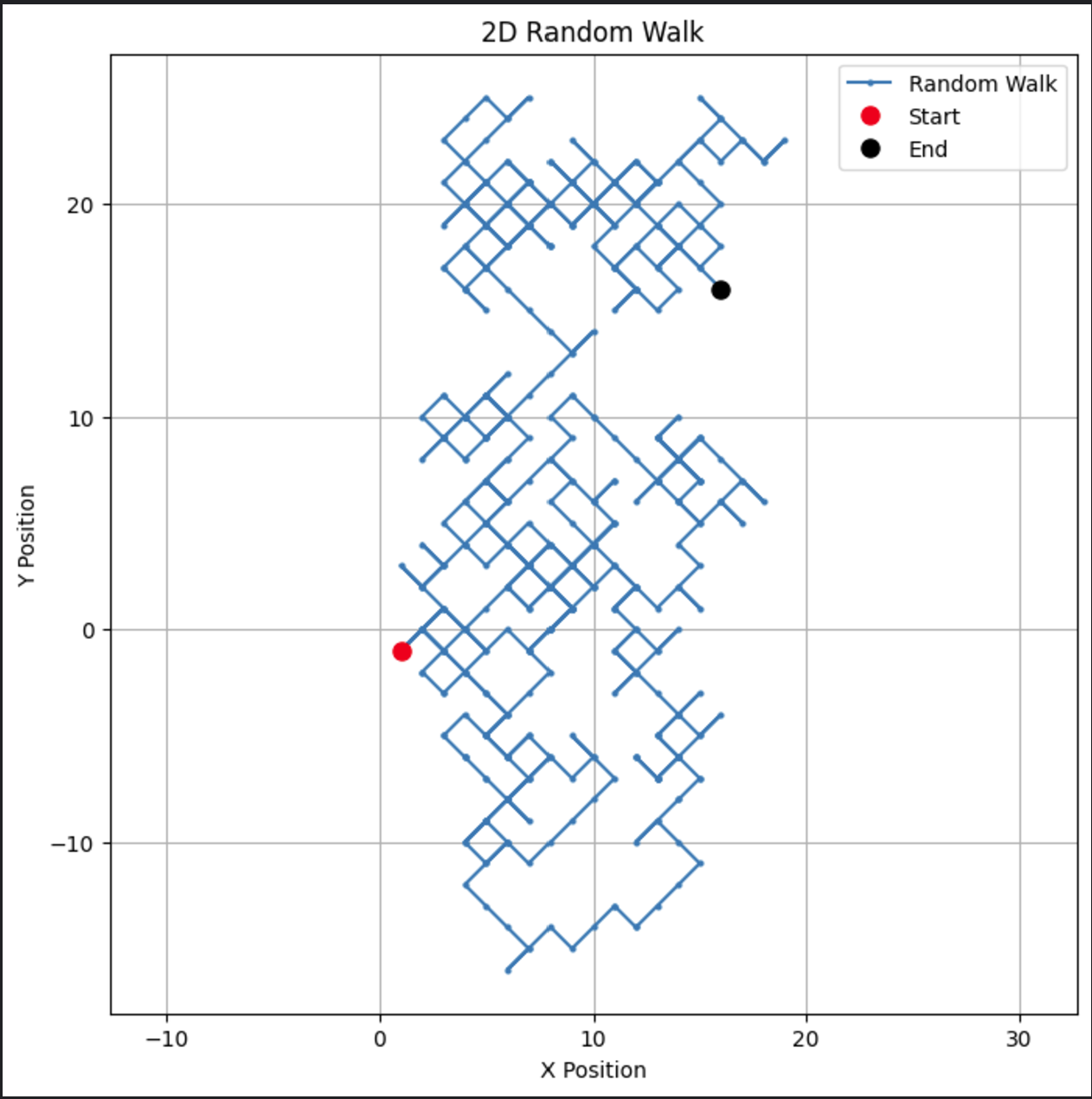
Questo tipo di passeggiata casuale bidimensionale potrebbe essere modificato per ospitare applicazioni come il movimento delle particelle o la modellazione spaziale.
Passeggiata casuale con bias
Infine, diamo un’occhiata a un esempio leggermente più complesso: una passeggiata casuale con bias. Per introdurre il bias, possiamo regolare le probabilità di ciascuna direzione del passo. Ad esempio, potremmo rendere i passi verso l’alto più probabili.
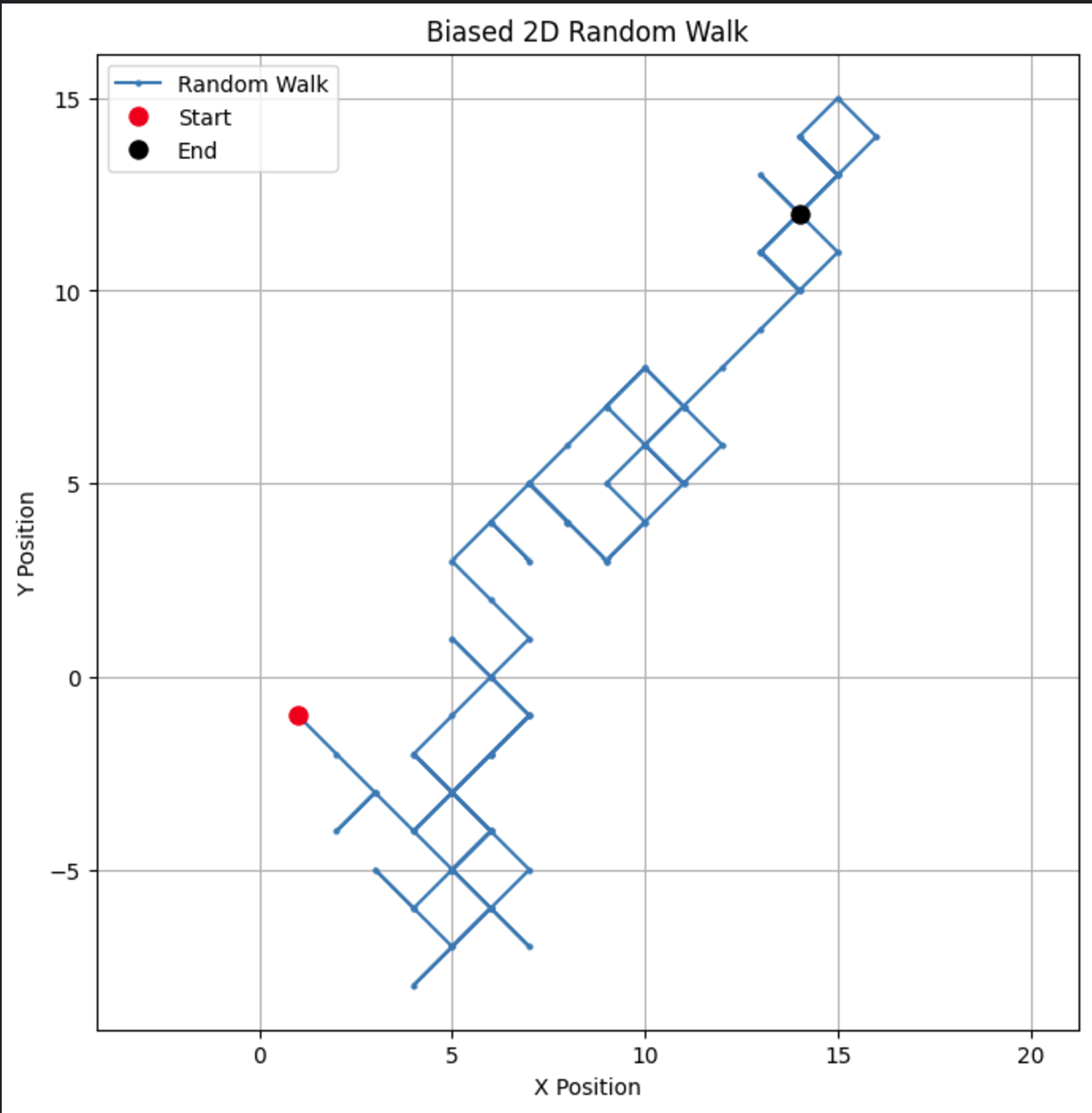
# Parametri n_steps = 100 bias = 0.7 # Probabilità di fare un passo +1 # Generare passi casuali biased nelle direzioni x e y x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) # Calcolare le posizioni x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Tracciare la passeggiata casuale 2D con bias plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Punto rosso per l'inizio plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Punto nero per la fine plt.title("Biased 2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Garantisce una scala uguale per entrambi gli assi plt.legend() plt.show()
Modificando il bias, puoi osservare come il cammino tende a favorire una direzione particolare, simulando scenari del mondo reale come il drift nei prezzi delle azioni o i modelli di migrazione degli animali.
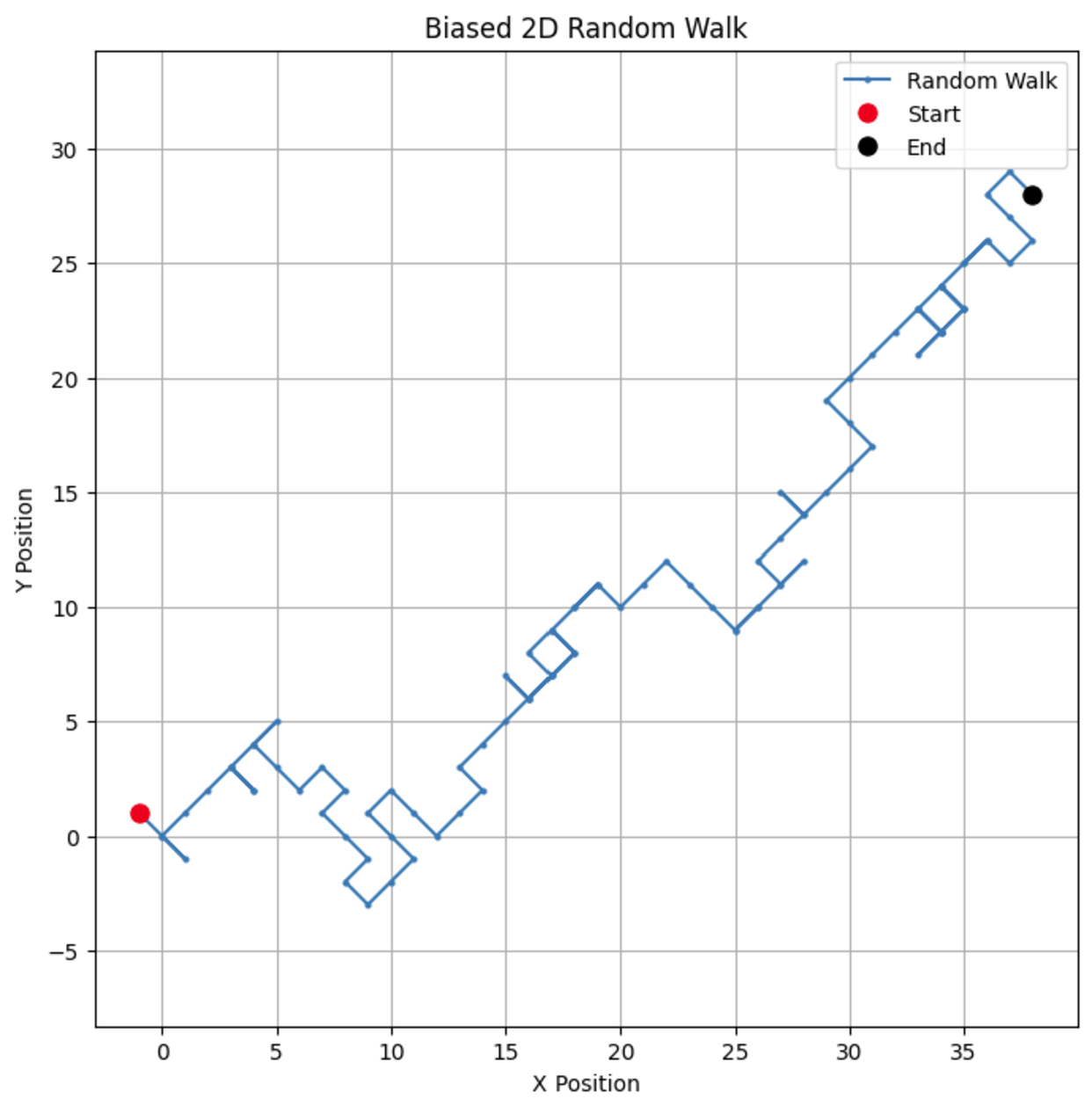
Cambiando il parametro di bias a 0.55, possiamo vedere una differenza drammatica nel modo in cui si comporta il modello. Sebbene abbia ancora un bias verso l’alto, il bias non è così forte, portando a più anelli e deviazioni.
Conclusione
I cammini casuali sono uno strumento di modellazione prezioso per i data scientist, applicabile in campi che vanno dalla fisica alla finanza e oltre. La loro capacità di modellare processi complessi e stocastici li rende indispensabili in molti scenari del mondo reale.
Hai fame di più? Dai un’occhiata a DataCamp’s suite di corsi su probabilità e statistica. Troverai tutti i tipi di ottimi corsi sia in Python che in R. Se sei interessato a contenuti più avanzati, dai un’occhiata al corso di DataCamp su Simulazione Statistica in Python e al tutorial Introduzione al Machine Learning. Oppure, se sei pronto a mettere alla prova le tue conoscenze, affronta alcuni di questi enigmi di probabilità.













