No meu primeiro curso de estatística baseado em programação na faculdade, meu professor propôs uma pergunta: como podemos modelar o movimento browniano de uma única partícula de pólen em uma tigela de água? Depois de várias tentativas equivocadas, eu e meus colegas de classe finalmente encontramos a resposta correta: uma caminhada aleatória. Mais tarde, descobri que esse modelo simples é usado para modelar todo tipo de coisas, desde movimentos de animais até flutuações de preços de ações.
Neste artigo, vamos explorar os fundamentos matemáticos das caminhadas aleatórias, examinar diferentes tipos e discutir suas aplicações. Parte do que torna a caminhada aleatória interessante é que ela é usada em tantas disciplinas diferentes. Além do meu exemplo, na física, ela ajuda a descrever o movimento de partículas; em finanças, ela modela as flutuações de preços das ações; e na biologia, ela explica os padrões de movimento dos animais. As caminhadas aleatórias capturam a aleatoriedade do mundo real, o que é fundamental para simular processos estocásticos.
Para aqueles que procuram construir uma base sólida nas estatísticas que fundamentam a teoria do passeio aleatório, recomendamos começar com o curso Introdução à Estatística em R ou o curso Introdução à Estatística em Python.
O que são passeios aleatórios?
Na teoria da probabilidade, um passeio aleatório é um modelo que descreve uma sequência de passos aleatórios que formam um caminho. Ou seja, poderíamos dizer que um passeio aleatório é um modelo matemático que descreve um caminho formado por uma sequência de passos, cada um determinado de forma independente e com uma certa probabilidade. Essa estocasticidade torna os passeios aleatórios inerentemente imprevisíveis.
Imagine uma pessoa dando um passo em uma direção aleatória a cada momento. Com o tempo, seu caminho forma uma trilha imprevisível e sinuosa. Apesar de sua simplicidade, esse conceito possui uma profundidade e versatilidade surpreendentes, modelando vários cenários do mundo real que envolvem aleatoriedade.
Uma explicação conceitual de um passeio aleatório. Imagem cortesia de napkin.ai.
A ideia de passeios aleatórios remonta aos primeiros estudos de probabilidade. Um dos exemplos mais antigos, frequentemente chamado de passeio do bêbado, ilustra como uma pessoa que dá passos aleatórios vagará erraticamente em vez de se mover previsivelmente em direção a um destino. Essa aleatoriedade, combinada com a suposição de que cada passo é independente dos anteriores, lançou as bases para os modelos modernos de passeio aleatório.
Compreendendo a Matemática dos Passeios Aleatórios
Para entender os passeios aleatórios, vamos começar com um caso simples: um passeio aleatório unidimensional (1D).Imagine uma partícula em uma linha numérica. Ela pode se mover tanto +1 quanto -1 ao longo da linha numérica a cada passo. Cada movimento é determinado por uma probabilidade igual de ir para a direita ou para a esquerda. Com o tempo, a posição da partícula forma uma distribuição de probabilidade que se espalha, representando a probabilidade de encontrá-la em várias localizações.
Esse princípio pode ser expandido para duas ou três dimensões. Em uma caminhada aleatória bidimensional (2D), a partícula se move em um plano e pode dar passos em qualquer uma das quatro direções cardeais (cima, baixo, esquerda, direita) com igual probabilidade. Da mesma forma, em uma caminhada aleatória tridimensional (3D), a partícula se move no espaço e pode dar passos em qualquer uma das seis direções possíveis (cima, baixo, esquerda, direita, para frente, para trás) com igual probabilidade. Essas caminhadas aleatórias de dimensões mais altas capturam cenários ainda mais complexos e realistas.
Uma característica definidora das caminhadas aleatórias é sua natureza estocástica, o que significa que cada passo depende apenas da posição atual e não dos passos anteriores. Isso as torna um tipo de processo de Markov—um conceito matemático onde o estado futuro depende apenas do estado presente, e não da sequência de eventos que o antecedeu. Esse movimento “sem memória”, combinado com distribuições de probabilidade que descrevem posições potenciais, fornece uma base matemática sólida para entender as caminhadas aleatórias.
Pode-se analisar um passeio aleatório usando propriedades estatísticas para entender seu comportamento ao longo do tempo. Isso envolve examinar aspectos como a distância esperada do ponto de partida, a distribuição de probabilidade de possíveis posições e a probabilidade de retornar à origem. Essas análises nos ajudam a quantificar aleatoriedade e previsibilidade, fornecer insights sobre padrões e fazer previsões.
Principais Propriedades dos Passeios Aleatórios
Os passeios aleatórios têm várias propriedades importantes que nos ajudam a entender seu comportamento e aplicações. Aqui estão alguns aspectos-chave a serem considerados:
Expectativa e variância
Em um passeio aleatório unidimensional, podemos calcular a distância esperada (ou posição média) a partir do ponto de partida ao longo do tempo. Se cada passo tiver uma probabilidade igual de se mover para a esquerda ou para a direita, a posição esperada após muitos passos permanece zero, o que implica que, em média, o caminhante permanece perto do ponto de partida.
No entanto, a variância da posição, que mede a dispersão de posições possíveis, aumenta a cada passo. Especificamente, em uma caminhada aleatória simétrica, a variância cresce linearmente com o número de passos, tornando-se um indicador útil da distância típica da origem ao longo do tempo.
Autocorrelação
Enquanto caminhadas aleatórias simples não têm correlação entre os passos (cada passo é independente do anterior), certos tipos de caminhadas aleatórias introduzem autocorrelação, onde os passos passados podem influenciar os futuros. Por exemplo, em uma caminhada aleatória enviesada, os passos podem ter uma leve tendência em uma direção, tornando as posições mais previsíveis.
A autocorrelação em uma caminhada aleatória impacta como modelamos e prevemos a progressão da caminhada. Isso é especialmente relevante em aplicações onde o comportamento passado influencia os passos futuros, como em certos modelos financeiros.
Teorema do limite central
O teorema do limite central (TLC) nos diz que a soma de um grande número de variáveis aleatórias independentes tende a seguir uma distribuição normal (ou gaussiana), independentemente da distribuição original. No contexto de caminhadas aleatórias, isso significa que conforme o número de passos aumenta, a distribuição das posições tende a se assemelhar a uma distribuição normal. Essa é uma propriedade útil porque nos permite aproximar a probabilidade de encontrar o caminhante a certas distâncias do ponto de partida.
Lei dos grandes números
A lei dos grandes números (LGN) explica que conforme o número de tentativas ou passos aumenta, a média dos resultados converge para a média verdadeira. Para caminhadas aleatórias, isso significa que enquanto a posição média permanece zero, a variância e o intervalo de posições possíveis crescem de forma previsível a cada passo adicional. Esse princípio ajuda a preencher a lacuna entre a aleatoriedade pura e padrões estatísticos previsíveis em amostras grandes.
Tipos de Caminhadas Aleatórias
As caminhadas aleatórias variam amplamente dependendo das regras que regem cada passo. Esses tipos influenciam o comportamento da caminhada. Alguns são projetados para ambientes simples ou estruturados, enquanto outros estão equipados para fenômenos do mundo real mais complexos. Vamos explorar alguns dos tipos mais comuns de caminhadas aleatórias.
1D, 2D e 3D caminhadas aleatórias
A dimensionalidade de uma caminhada aleatória desempenha um papel fundamental em seu comportamento. Em uma caminhada aleatória de 1D, cada passo é ou avançar ou retroceder ao longo de uma linha. Isso torna a caminhada relativamente fácil de modelar e prever.
No entanto, à medida que avançamos para caminhadas em 2D (plano) e 3D (espaço), os caminhos possíveis aumentam significativamente, introduzindo novo comportamento. Por exemplo, em uma caminhada aleatória em 2D, a probabilidade de retornar ao ponto de partida permanece alta, enquanto em uma caminhada aleatória em 3D, essa probabilidade diminui.
Essa mudança é importante em campos como física e química, onde partículas podem difundir de maneira diferente dependendo das restrições dimensionais.
Caminhada aleatória em grade
Em uma caminhada aleatória em grade, o movimento é restrito a pontos discretos em uma grade ou rede. Esse tipo de caminhada é comumente utilizado em física e teoria de redes, onde os nós são dispostos em uma grade, e o movimento só pode ocorrer para nós vizinhos.
Um exemplo comum é uma grade 2D, onde cada passo permite o movimento para pontos adjacentes em uma grade cartesiana. Essa restrição simplifica a modelagem ao limitar os caminhos de movimento, o que é útil ao simular redes complexas ou estruturas moleculares.
Caminhada aleatória gaussiana
Em uma caminhada aleatória gaussiana, o tamanho de cada passo é determinado por uma distribuição gaussiana (ou normal). Em vez de se mover por uma distância fixa, o tamanho do passo varia de acordo com uma distribuição em forma de sino, com a maioria dos passos sendo pequenos e alguns saltos maiores ocasionais. Esse tipo de caminhada é frequentemente utilizado em modelagem financeira para considerar a variabilidade nas mudanças de preço de ativos.
Caminhadas aleatórias heterogêneas e enviesadas
Caminhadas aleatórias heterogêneas e enviesadas permitem variação na direção e tamanho do passo com base em certas probabilidades. Essa flexibilidade as torna mais adaptáveis a cenários do mundo real.
Em uma caminhada aleatória heterogênea, a probabilidade de se mover em qualquer direção pode mudar com base na localização ou condições externas. Por exemplo, animais em busca de alimentos podem favorecer áreas com recursos conhecidos, criando uma caminhada aleatória enviesada. Essas caminhadas são úteis para estudar comportamentos que dependem de fatores contextuais.
Caminhada aleatória com derivação
Em uma caminhada aleatória com deriva, há uma tendência consistente de se mover em uma direção. Por exemplo, os preços das ações podem apresentar uma tendência geral de alta ao longo do tempo, apesar das flutuações diárias. A deriva nessas caminhadas representa uma força externa ou tendência influenciando o caminho. Esse tipo é frequentemente visto em finanças, onde os modelos incorporam um termo de deriva para representar crescimento ou declínio, fornecendo uma abordagem mais realista para prever os preços dos ativos e as tendências de mercado.
Cada um desses tipos de caminhada aleatória serve a um propósito único, oferecendo diferentes maneiras de modelar comportamentos aleatórios, porém estruturados. As restrições dimensionais, distribuição de passos e presença de deriva ou viés tornam as caminhadas aleatórias altamente versáteis para modelagem de dados e simulação em diversas áreas.
Aplicações do Mundo Real das Caminhadas Aleatórias
As caminhadas aleatórias são mais do que simples construções teóricas; elas desempenham um papel essencial em muitas aplicações práticas em diversas disciplinas. Vamos explorar como as caminhadas aleatórias informam a resolução de problemas do mundo real em diversos setores.
Aplicações em ciência de dados e aprendizado de máquina
Ciência da computação
Passeios aleatórios fundamentam vários algoritmos de ciência da computação, como amostragem aleatória, travessia de gráficos da web e segmentação de imagens. Por exemplo, O algoritmo PageRank do Google usou passeios aleatórios para classificar páginas da web com base em sua relevância, simulando como um usuário poderia navegar aleatoriamente entre links na internet.
Extração de características
No aprendizado de máquina, passeios aleatórios podem ajudar a extrair características destacando relacionamentos entre pontos de dados. Por exemplo, na análise de redes, passeios aleatórios podem revelar clusters ou comunidades, auxiliando em tarefas como sistemas de recomendação e análise de redes sociais.
Deteção de anomalias
Passeios aleatórios também podem ser usados para detectar anomalias em conjuntos de dados. Por exemplo, se os pontos de dados se desviarem significativamente de um caminho típico em um modelo de passeio aleatório, esses pontos podem indicar eventos incomuns ou erros nos dados. A detecção de anomalias é especialmente valiosa em áreas como segurança cibernética e detecção de fraudes.
Simulando processos estocásticos
As caminhadas aleatórias simulam processos estocásticos, ou aleatórios, permitindo que cientistas de dados modelem fenômenos imprevisíveis do mundo real. Ao simular caminhadas aleatórias, podemos obter insights sobre sistemas nos quais a previsão precisa é desafiadora, como padrões climáticos ou comportamento do cliente.
Previsão de séries temporais
Na análise de séries temporais, as caminhadas aleatórias formam a base para certos modelos de previsão, incluindo a hipótese da caminhada aleatória em finanças. Esses modelos assumem que os valores futuros em uma série temporal dependem exclusivamente do valor mais recente, sem correlação com tendências passadas.Para mais informações sobre previsão de séries temporais, confira ARIMA para Previsão de Séries Temporais: Um Guia Completo. Além disso, faça nosso curso Previsão em R com o Professor Hyndman, que conecta modelos de caminhada aleatória a métodos de previsão ingênuos e sazonalmente ingênuos.
Aplicações em outros campos
Finanças
Um dos usos mais notáveis das caminhadas aleatórias está na modelagem financeira, especialmente na previsão de preços de ações. A hipótese de mercado eficiente sugere que os movimentos de preços das ações são essencialmente aleatórios, pois novas informações são instantaneamente absorvidas, tornando os preços futuros imprevisíveis. As caminhadas aleatórias podem ser usadas para modelar as mudanças nos preços das ações ao longo do tempo, ilustrando como os preços flutuam sem um caminho previsível.
Matemática
Na matemática pura, as caminhadas aleatórias fornecem soluções para problemas complexos. Por exemplo, elas são úteis na resolução da equação de Laplace, na análise de redes e na exploração da combinatória.
Física e química
Nas ciências físicas, as caminhadas aleatórias são cruciais para a modelagem de processos de difusão, como a forma como as moléculas se espalham por um meio. O movimento browniano, onde partículas suspensas em um fluido se movem de forma imprevisível devido a colisões com moléculas ao redor, é um exemplo clássico que pode ser simulado com precisão usando caminhadas aleatórias. Foi assim que eu aprendi sobre caminhadas aleatórias pela primeira vez.
Biologia
As caminhadas aleatórias são valiosas na ecologia para estudar os padrões de movimento dos animais. Animais em busca de recursos podem parecer se mover em uma caminhada aleatória, às vezes com viés em direção a regiões com recursos conhecidos. Outros conceitos biológicos, como a dispersão de populações ou genes, frequentemente podem ser modelados com princípios de caminhada aleatória, tornando mais fácil entender e prever mudanças dentro dos ecossistemas.
Casos Especiais e Variantes de Caminhadas Aleatórias
Além da caminhada aleatória clássica, várias variantes avançadas estendem o conceito para se adequar a aplicações especializadas.
Caminhadas autoevitantes
Uma caminhada autoevitante é uma caminhada aleatória na qual o caminho não revisita nenhuma posição que já passou. Essa variante é particularmente útil em campos como a química de polímeros, onde pode modelar como cadeias de polímeros se formam sem se cruzar. Como cada passo evita pontos visitados anteriormente, as caminhadas autoevitantes são mais restritas do que as caminhadas aleatórias tradicionais. Isso significa que são desafiadoras computacionalmente, mas úteis para entender caminhos não sobrepostos em espaços confinados.
Ramificação
Nas caminhadas aleatórias ramificadas, o caminho pode se dividir em múltiplos ramos, sendo que cada ramo segue uma caminhada aleatória. Esse tipo de caminhada é fundamental na modelagem de processos de ramificação, como a divisão celular ou a propagação de informações por meio de redes. Cada “ramo” representa um caminho aleatório independente que se origina de uma fonte comum.
Caminhadas correlacionadas
As caminhadas correlacionadas levam esse conceito um passo adiante, onde a direção de cada passo é parcialmente influenciada pelo passo anterior. Essa variante é útil para modelar inércia em sistemas onde as mudanças ocorrem gradualmente, em vez de aleatoriamente. Caminhadas correlacionadas são frequentemente aplicadas em finanças para simular tendências de preços ou em ecologia de movimento para entender como os animais navegam em seus ambientes com alguma memória de sua direção passada.
Caminhadas com eliminação de loops
Uma caminhada com eliminação de loops é uma variante onde os loops, ou caminhos que se cruzam, são removidos conforme se formam. Cada vez que um passo revisita uma posição, o loop intermediário é apagado, deixando um caminho simplificado e não repetitivo. As caminhadas com eliminação de loops são comumente aplicadas em análise de redes e algoritmos de geração de labirintos, pois criam caminhos que evitam a redundância.
Implementando Caminhadas Aleatórias em Python
Vamos tentar implementar uma caminhada aleatória em Python.Para começar, certifique-se de ter o Python instalado (vamos usar o Python 3.10) e as bibliotecas necessárias disponíveis. Você pode instalar quaisquer bibliotecas ausentes usando o pip. Aqui está o que vamos usar:
import numpy as np # para operações numéricas e gerar passos aleatórios import matplotlib.pyplot as plt # para plotar e visualizar as caminhadas aleatórias
Caminhada aleatória 1D
Vamos começar com uma caminhada aleatória unidimensional simples, onde cada passo é +1 ou -1, escolhido aleatoriamente.
# Parâmetros n_steps = 100 # Número de passos # Gerar passos aleatórios: +1 ou -1 steps = np.random.choice([-1, 1], size=n_steps) # Calcular posições positions = np.cumsum(steps) # Plotar a caminhada aleatória plt.figure(figsize=(10, 6)) plt.plot(positions, marker='o', linestyle='-', markersize=4) plt.title("1D Random Walk") plt.xlabel("Step") plt.ylabel("Position") plt.grid(True) plt.show()
Isso gera um passeio aleatório simples e visualiza a progressão ao longo do tempo. Aqui está a saída quando eu executo este código:
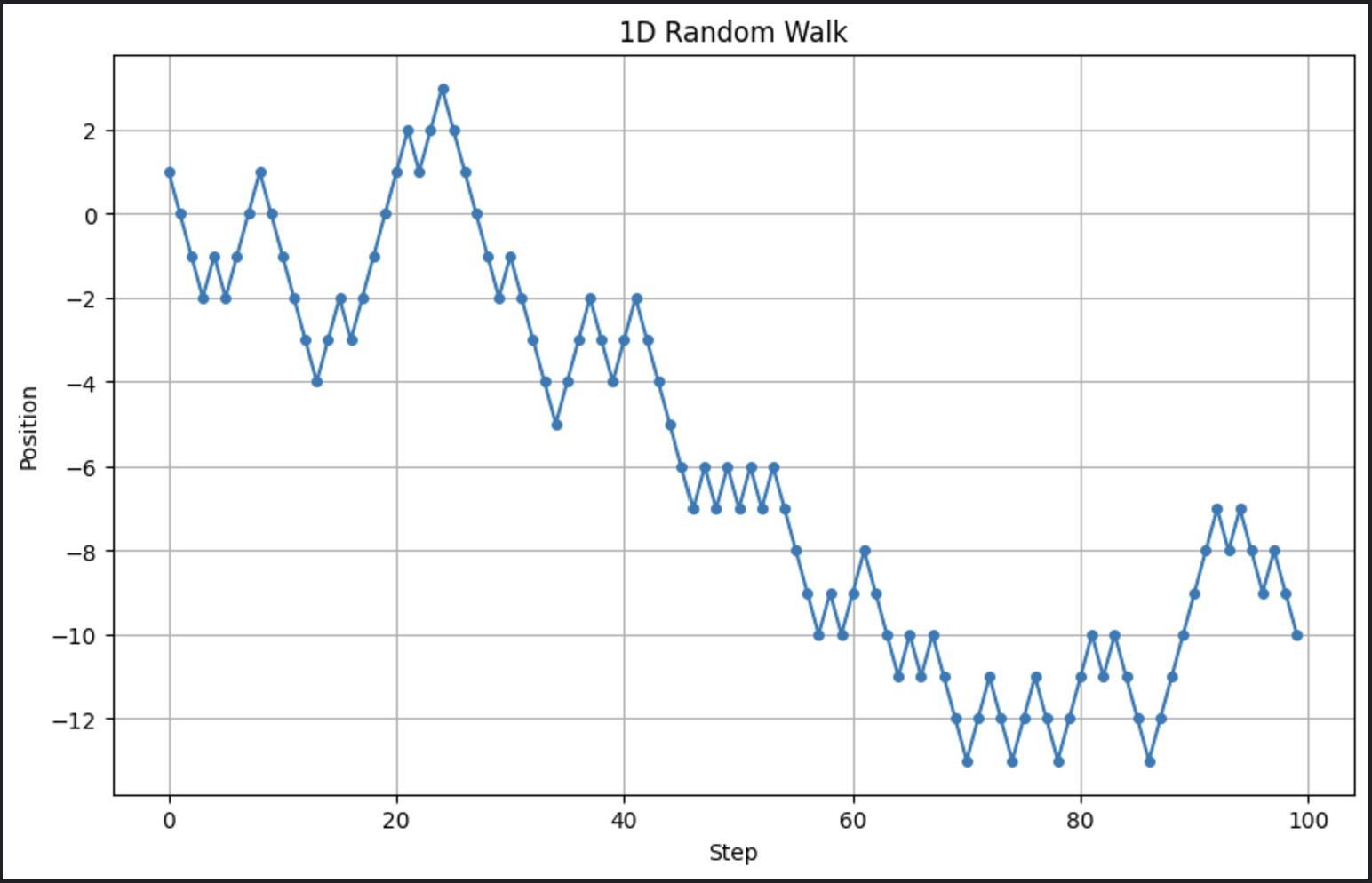
Agora lembre-se, estamos executando um modelo estocástico. Isso significa que toda vez que o executamos, a saída parecerá um pouco diferente.
Passeio aleatório 2D
Agora vamos estender o passeio aleatório para duas dimensões. A cada passo, a direção será escolhida aleatoriamente.
# Parâmetros n_steps = 500 # Gera passos aleatórios nas direções x e y x_steps = np.random.choice([-1, 1], size=n_steps) y_steps = np.random.choice([-1, 1], size=n_steps) # Calcula posições x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Plota o passeio aleatório 2D plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Ponto vermelho para o início plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Ponto preto para o fim plt.title("2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Garante escala igual para ambos os eixos plt.legend() plt.show()
Este código cria um caminho visualmente envolvente em duas dimensões.
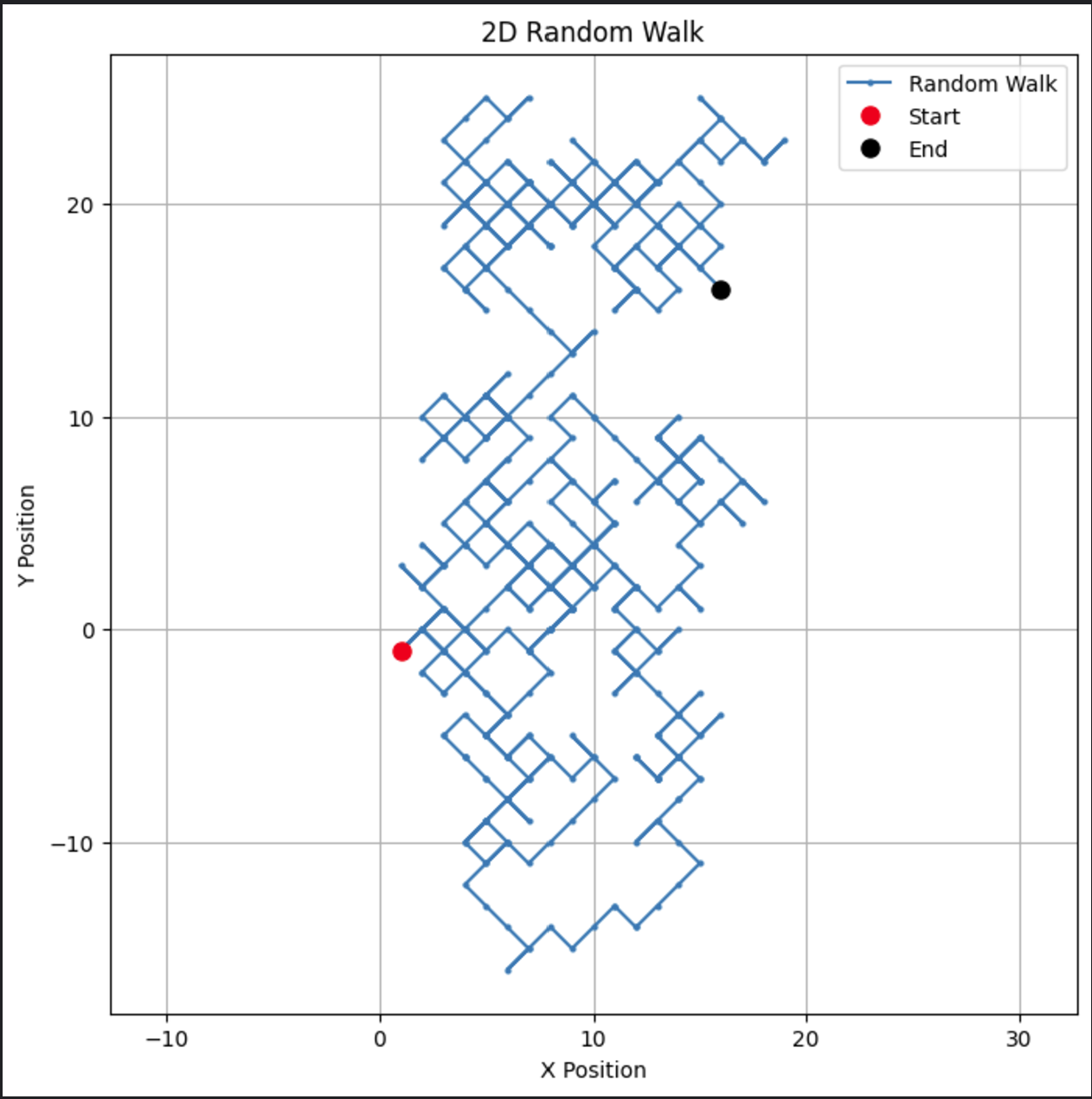
Este tipo de caminhada aleatória bidimensional poderia ser modificado para acomodar aplicações como movimento de partículas ou modelagem espacial.
Caminhada aleatória enviesada
Por fim, vamos ver um exemplo um pouco mais complexo: uma caminhada aleatória enviesada. Para introduzir viés, podemos ajustar as probabilidades de cada direção do passo. Por exemplo, poderíamos tornar os passos para cima mais prováveis.
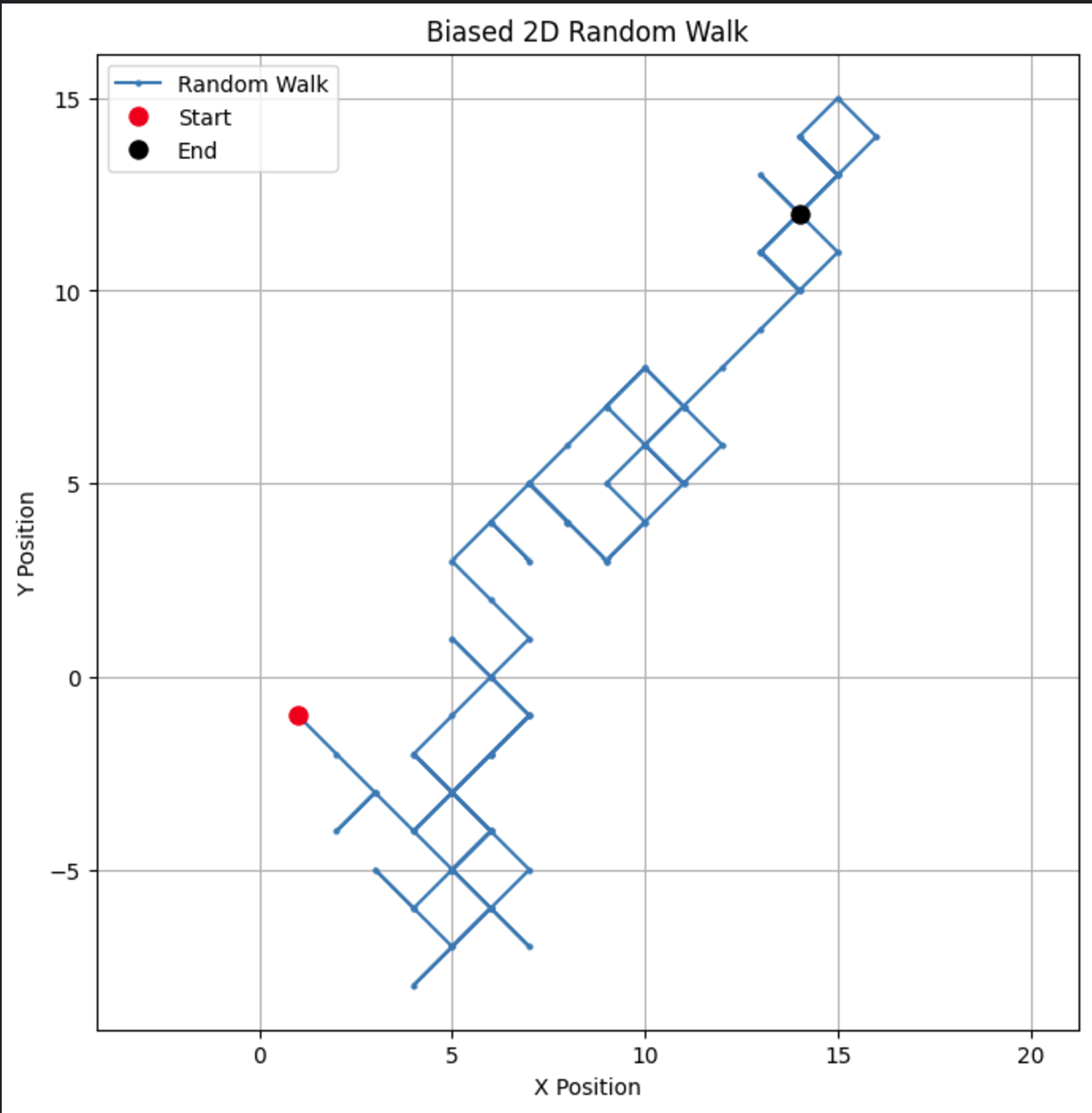
# Parâmetros n_steps = 100 bias = 0.7 # Probabilidade de dar um passo +1 # Gerar passos aleatórios enviesados nas direções x e y x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) # Calcular posições x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Plotar a caminhada aleatória 2D enviesada plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Ponto vermelho para início plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Ponto preto para fim plt.title("Biased 2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Garante escala igual para ambos os eixos plt.legend() plt.show()
Ao alterar o viés, você pode observar como o passeio tende a favorecer uma direção específica, simulando cenários do mundo real como a deriva nos preços das ações ou padrões de migração animal.
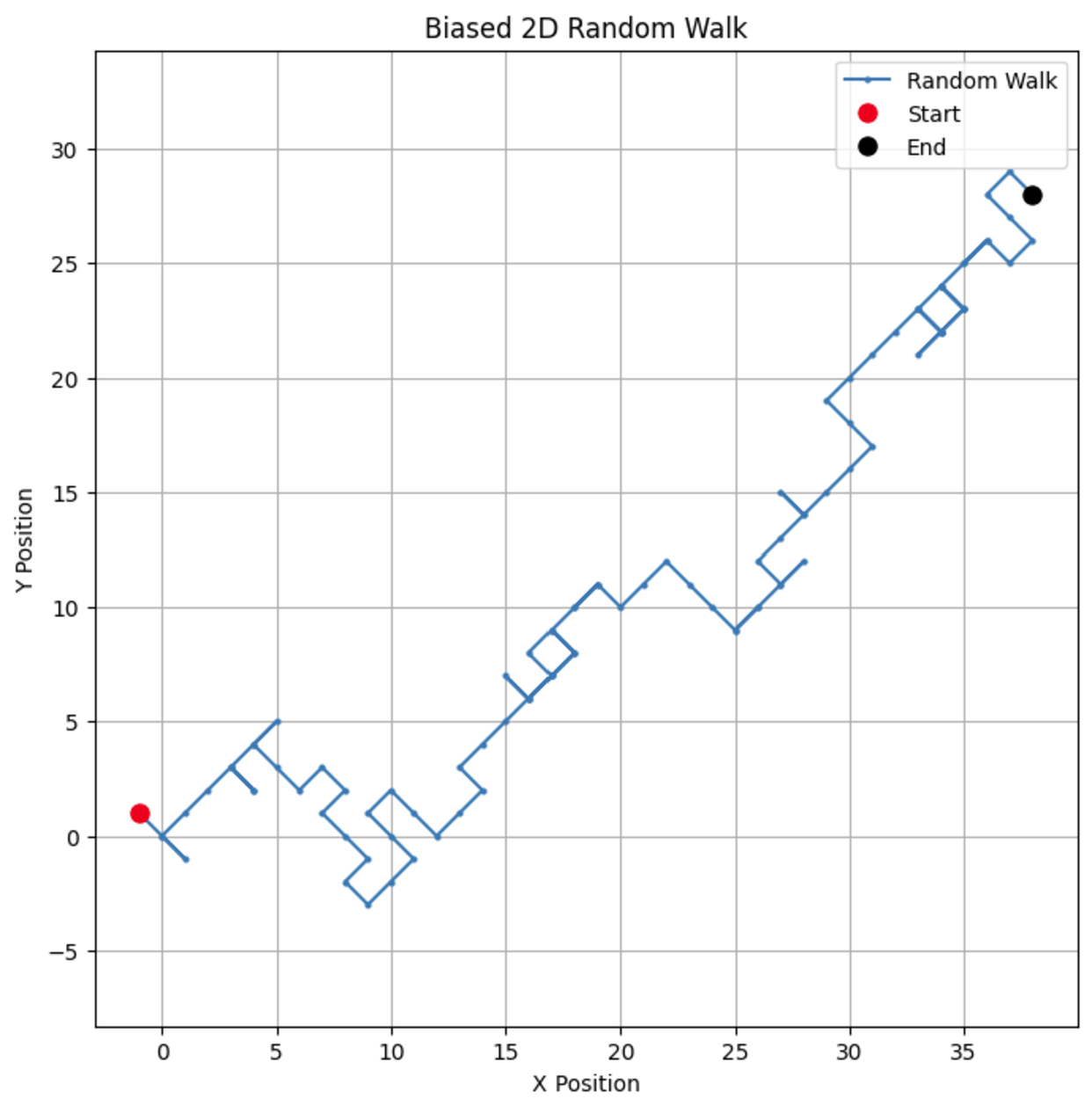
Se alterarmos o parâmetro de viés para 0,55, podemos ver uma diferença dramática na forma como o modelo se comporta. Embora ainda tenha um viés para cima, o viés não é tão forte, levando a mais voltas e desvios.
Conclusão
Os passeios aleatórios são uma ferramenta de modelagem valiosa para cientistas de dados, aplicável em campos que vão da física às finanças e além. Sua capacidade de modelar processos complexos e estocásticos os torna indispensáveis em muitos cenários do mundo real.
Com fome de mais? Confira a suite de cursos de probabilidade e estatística da DataCamp. Você encontrará todos os tipos de ótimos cursos em Python e R. Se você estiver interessado em conteúdo mais avançado, confira o curso da DataCamp sobre Simulação Estatística em Python e o tutorial Introdução ao Aprendizado de Máquina. Ou se estiver pronto para testar seus conhecimentos, enfrente alguns desses quebra-cabeças de probabilidade.













