In mijn eerste op codering gebaseerde statistiekcursus op de universiteit stelde mijn docent een vraag voor: hoe kunnen we de Brownse beweging van een enkel stuifmeeldeeltje in een schaaltje water modelleren? Na verschillende verkeerde pogingen kwamen mijn klasgenoten en ik uiteindelijk op het juiste antwoord: een willekeurige wandeling. Later leerde ik dat dit eenvoudige model wordt gebruikt om allerlei zaken te modelleren, van dierbewegingen tot schommelingen in aandelenprijzen.
In dit artikel zullen we de wiskundige grondslagen van willekeurige wandelingen verkennen, verschillende typen onderzoeken en hun toepassingen bespreken. Een deel van wat de willekeurige wandeling interessant maakt, is dat het wordt gebruikt in zoveel verschillende disciplines. Naast mijn voorbeeld helpt het in de natuurkunde bij het beschrijven van de beweging van deeltjes; in de financiën modelleert het schommelingen in aandelenprijzen; en in de biologie verklaart het bewegingspatronen van dieren. Willekeurige wandelingen vangen willekeur in de echte wereld, wat essentieel is voor het simuleren van stochastische processen.
Voor degenen die een sterke basis willen opbouwen in de statistiek die ten grondslag ligt aan de theorie van de willekeurige wandeling, raden wij aan te beginnen met de cursus Inleiding tot Statistiek in R of de cursus Inleiding tot Statistiek in Python.
Wat Zijn Willekeurige Wandelingen?
In de kansrekening is een willekeurige wandeling een model dat een reeks willekeurige stappen beschrijft die een pad vormen. Anders gezegd is een willekeurige wandeling een wiskundig model dat een pad beschrijft dat wordt gevormd door een reeks stappen, elk onafhankelijk en met een bepaalde kans bepaald. Deze stochastiek maakt willekeurige wandelingen inherent onvoorspelbaar.
Stel je voor dat een persoon bij elk moment een stap in een willekeurige richting zet. Na verloop van tijd vormt hun pad een onvoorspelbaar, kronkelend spoor. Ondanks zijn eenvoud heeft dit concept verrassende diepgang en veelzijdigheid, waarbij verschillende realistische scenario’s die willekeurigheid omvatten, worden gemodelleerd.
Een conceptuele uitleg van een willekeurige wandeling. Afbeelding met dank aan napkin.ai.
Het idee van willekeurige wandelingen dateert uit de vroege kansstudies. Een van de vroegste voorbeelden, vaak de wandeling van de dronkaard genoemd, illustreert hoe een persoon die willekeurig stapt, onvoorspelbaar zal zwerven in plaats van voorspelbaar naar een bestemming te bewegen. Deze willekeurigheid, gecombineerd met de aanname dat elke stap onafhankelijk is van de vorige, legde de basis voor moderne modellen van willekeurige wandelingen.
De Wiskunde van Willekeurige Wandelingen Begrijpen
Om willekeurige wandelingen te begrijpen, beginnen we met een eenvoudig geval: een eendimensionale (1D) willekeurige wandeling.Stel je een deeltje voor op een getallenlijn. Het kan met elke stap ofwel +1 ofwel -1 langs de getallenlijn bewegen. Elke beweging wordt bepaald door een gelijke kans om naar rechts of naar links te stappen. Na verloop van tijd vormt de positie van het deeltje een kansverdeling die zich verspreidt en de waarschijnlijkheid vertegenwoordigt om het op verschillende locaties te vinden.
Dit principe kan worden uitgebreid naar twee of drie dimensies. In een tweedimensionale (2D) willekeurige wandeling beweegt het deeltje op een vlak en kan het met gelijke waarschijnlijkheid in een van de vier hoofd richtingen stappen (omhoog, omlaag, links, rechts). Evenzo, in een driedimensionale (3D) willekeurige wandeling, beweegt het deeltje in de ruimte en kan het met gelijke waarschijnlijkheid in een van de zes mogelijke richtingen stappen (omhoog, omlaag, links, rechts, vooruit, achteruit). Deze hoger-dimensionale willekeurige wandelingen vangen zelfs nog complexere en realistischere scenario’s.
Een kenmerkende eigenschap van willekeurige wandelingen is hun stochastische natuur, wat betekent dat elke stap alleen afhangt van de huidige positie en niet van de voorgaande stappen. Dit maakt ze een type Markov-proces — een wiskundig concept waarbij de toekomstige staat uitsluitend afhangt van de huidige staat, niet van de volgorde van gebeurtenissen die eraan voorafgingen. Deze “geheugenvrije” beweging, gecombineerd met waarschijnlijkheidsverdelingen die potentiële posities beschrijven, biedt een solide wiskundige basis voor het begrijpen van willekeurige wandelingen.
We kunnen een willekeurige wandeling analyseren met behulp van statistische eigenschappen om het gedrag ervan in de loop van de tijd te begrijpen. Dit houdt in dat we aspecten onderzoeken zoals de verwachte afstand van het startpunt, de waarschijnlijkheidsverdeling van mogelijke posities en de kans om naar de oorsprong terug te keren. Deze analyses helpen ons om willekeurigheid en voorspelbaarheid te kwantificeren, inzicht te geven in patronen en voorspellingen te doen.
Belangrijke Eigenschappen van Willekeurige Wandelingen
Willekeurige wandelingen hebben verschillende belangrijke eigenschappen die ons helpen hun gedrag en toepassingen te begrijpen. Hier zijn enkele belangrijke aspecten om te overwegen:
Verwachting en variantie
In een eendaagse willekeurige wandeling kunnen we de verwachte afstand (of gemiddelde positie) van het startpunt in de loop van de tijd berekenen. Als elke stap een gelijke kans heeft om naar links of naar rechts te bewegen, blijft de verwachte positie na veel stappen nul, wat betekent dat de wandelaar gemiddeld dicht bij het startpunt blijft.
De variantie van de positie, die de spreiding of verspreiding van mogelijke posities meet, neemt toe met elke stap. Specifiek, in een symmetrische willekeurige wandeling, groeit de variantie lineair met het aantal stappen, waardoor het een bruikbare indicator is van de typische afstand van de oorsprong in de loop van de tijd.
Autocorrelatie
Terwijl eenvoudige willekeurige wandelingen geen correlatie hebben tussen stappen (elke stap is onafhankelijk van de vorige), introduceren bepaalde soorten willekeurige wandelingen autocorrelatie, waarbij eerdere stappen toekomstige kunnen beïnvloeden. Bijvoorbeeld, in een bevooroordeelde willekeurige wandeling, kunnen stappen een lichte neiging hebben in één richting, waardoor posities voorspelbaarder worden.
Autocorrelatie in een willekeurige wandeling heeft invloed op hoe we de voortgang van de wandeling modelleren en voorspellen. Dit is vooral relevant in toepassingen waarbij het verleden gedrag toekomstige stappen beïnvloedt, zoals bepaalde financiële modellen.
Centrale limietstelling
Het centrale limietstelling (CLT) vertelt ons dat de som van een groot aantal onafhankelijke willekeurige variabelen neigt om een normale (of Gaussische) verdeling te volgen, ongeacht de oorspronkelijke verdeling. In de context van willekeurige wandelingen betekent dit dat naarmate het aantal stappen toeneemt, de verdeling van posities neigt naar een normale verdeling. Dit is een nuttige eigenschap omdat het ons in staat stelt om de waarschijnlijkheid te benaderen van het vinden van de wandelaar op bepaalde afstanden van het startpunt.
Wet van de grote getallen
De wet van de grote getallen (LLN) legt uit dat naarmate het aantal pogingen of stappen toeneemt, het gemiddelde van de resultaten convergeert naar het ware gemiddelde. Voor willekeurige wandelingen betekent dit dat terwijl de gemiddelde positie nul blijft, de variantie en het bereik van mogelijke posities voorspelbaar groeien met elke extra stap. Dit principe helpt de kloof te overbruggen tussen pure willekeur en voorspelbare statistische patronen in grote steekproeven.
Soorten Willekeurige Wandelingen
Willekeurige wandelingen variëren sterk, afhankelijk van de regels die elke stap bepalen. Deze types beïnvloeden hoe de wandeling zich gedraagt. Sommige zijn ontworpen voor eenvoudige of gestructureerde omgevingen, terwijl andere zijn uitgerust voor complexere, realistische fenomenen. Laten we enkele van de meest voorkomende types van willekeurige wandelingen verkennen.
1D, 2D en 3D willekeurige wandelingen
De dimensionaliteit van een willekeurige wandeling speelt een fundamentele rol in zijn gedrag. In een 1D willekeurige wandeling is elke stap ofwel een stap vooruit of een stap achteruit langs een lijn. Dit maakt de wandeling relatief eenvoudig te modelleren en te voorspellen.
Echter, naarmate we overgaan naar 2D (vlak) en 3D (ruimte) wandelingen, neemt het aantal mogelijke paden aanzienlijk toe, wat nieuw gedrag introduceert. In een 2D willekeurige wandeling blijft de kans om naar het startpunt terug te keren hoog, terwijl deze kans in een 3D willekeurige wandeling afneemt.
Deze verandering is belangrijk in vakgebieden zoals de natuurkunde en scheikunde, waar deeltjes mogelijk anders diffunderen afhankelijk van de dimensionale beperkingen.
Lattice random walk
Bij een lattice random walk is de beweging beperkt tot discrete punten op een rooster of lattice. Dit type wandeling wordt vaak gebruikt in de natuurkunde en netwerktheorie, waar knooppunten in een rooster zijn gerangschikt en beweging alleen kan plaatsvinden naar naburige knooppunten.
Een veelvoorkomend voorbeeld is een 2D-rooster, waar elke stap beweging naar aangrenzende punten op een cartesisch rooster mogelijk maakt. Deze beperking vereenvoudigt het modelleren door de bewegingspaden te beperken, wat nuttig is bij het simuleren van complexe netwerken of moleculaire structuren.
Gaussiaanse random walk
In een Gaussische random walk wordt de grootte van elke stap bepaald door een Gaussische (of normale) verdeling. In plaats van te bewegen over een vaste afstand, varieert de stapgrootte volgens een klokvormige verdeling, waarbij de meeste stappen klein zijn en af en toe grotere sprongen voorkomen. Dit type wandeling wordt vaak gebruikt in financiële modellen om rekening te houden met de variabiliteit in veranderingen van activa prijzen.
Heterogene en bevooroordeelde random walks
Heterogene en bevooroordeelde random walks staan variatie in staprichting en grootte toe op basis van bepaalde waarschijnlijkheden. Deze flexibiliteit maakt ze beter aanpasbaar aan situaties in de echte wereld.
In een heterogene random walk kan de kans om in welke richting dan ook te bewegen veranderen op basis van locatie of externe omstandigheden. Bijvoorbeeld, dieren die voedsel zoeken, kunnen gebieden met bekende bronnen bevoordelen, wat leidt tot een bevooroordeelde random walk. Deze wandelingen zijn nuttig voor het bestuderen van gedragingen die afhankelijk zijn van contextuele factoren.
Random walk met drift
In een willekeurige wandeling met drift is er een consistente neiging om in één richting te bewegen. Bijvoorbeeld, aandelenprijzen kunnen in de loop der tijd een algemene opwaartse trend vertonen ondanks dagelijkse schommelingen. De drift in deze wandelingen vertegenwoordigt een externe kracht of trend die het pad beïnvloedt. Dit type wordt vaak gezien in de financiën, waar modellen een driftterm opnemen om groei of achteruitgang te vertegenwoordigen, wat een realistischere benadering biedt voor het voorspellen van activaprijzen en markttrends.
Elk van deze types willekeurige wandelingen heeft een uniek doel en biedt verschillende manieren om willekeurig, maar gestructureerd, gedrag te modelleren. De dimensionale beperkingen, verdeling van stappen en de aanwezigheid van drift of bias maken willekeurige wandelingen zeer veelzijdig voor datamodellering en simulatie in diverse velden.
Toepassingen van Willekeurige Wandelingen in de Praktijk
Willekeurige wandelingen zijn meer dan alleen theoretische constructen; ze spelen een essentiële rol in veel praktische toepassingen in verschillende disciplines. Laten we verkennen hoe willekeurige wandelingen bijdragen aan het oplossen van echte problemen in verschillende sectoren.
Toepassingen in datawetenschap en machine learning
Informatica
Willekeurige wandelingen liggen ten grondslag aan verschillende algoritmen in de informatica, zoals willekeurige steekproeven, webgrafiekdoorlopen en beeldsegmentatie. Bijvoorbeeld, het PageRank-algoritme van Google gebruikte willekeurige wandelingen om webpagina’s te rangschikken op basis van hun relevantie, waarbij werd gesimuleerd hoe een gebruiker willekeurig tussen links op het internet zou navigeren.
Kenmerkenextractie
In machine learning kunnen willekeurige wandelingen helpen bij het extraheren van kenmerken door relaties binnen datapunten te benadrukken. Bijvoorbeeld, in netwerkanalyse kunnen willekeurige wandelingen clusters of gemeenschappen onthullen, wat helpt bij taken zoals aanbevelingssystemen en sociale netwerkanalyse.
Anomaliedetectie
Willekeurige wandelingen kunnen ook worden gebruikt om anomalieën in datasets te detecteren. Bijvoorbeeld, als datapunten significant afwijken van een typisch pad in een willekeurige wandelingsmodel, kunnen deze punten ongebruikelijke gebeurtenissen of fouten in de gegevens aanduiden. Anomaliedetectie is vooral waardevol in velden zoals cybersecurity en fraudedetectie.
Het simuleren van stochastische processen
Willekeurige wandelingen simuleren stochastische, of willekeurig bepaalde, processen, waardoor datawetenschappers onvoorspelbare verschijnselen in de echte wereld kunnen modelleren. Door het simuleren van willekeurige wandelingen kunnen we inzicht krijgen in systemen waarbij nauwkeurige voorspellingen moeilijk zijn, zoals weerpatronen of klantengedrag.
Tijdreeksen voorspellen
In tijdreeksanalyse vormen willekeurige wandelingen de basis voor bepaalde voorspellingsmodellen, waaronder de willekeurige wandelhypothese in de financiën. Deze modellen gaan ervan uit dat toekomstige waarden in een tijdreeks uitsluitend afhankelijk zijn van de meest recente waarde, zonder correlatie met eerdere trends.Voor meer informatie over tijdreeksen voorspellen, bekijk ARIMA voor Tijdreeksen Voorspellingen: Een Compleet Gids. Neem ook onze Voorspellen in R cursus met Professor Hyndman, die willekeurige wandelmodellen verbindt met naïeve en seizoensgebonden naïeve voorspellingsmethoden.
Toepassingen in andere vakgebieden
Financiën
Een van de meest opmerkelijke toepassingen van willekeurige wandelingen is in financiële modellering, vooral voor het voorspellen van aandelenprijzen. De efficiënte-markthypothese suggereert dat de bewegingen van aandelenprijzen in wezen willekeurig zijn, omdat nieuwe informatie onmiddellijk wordt opgenomen, waardoor toekomstige prijzen onvoorspelbaar zijn. Willekeurige wandelingen kunnen worden gebruikt om veranderingen in aandelenprijzen in de loop van de tijd te modelleren, waarbij wordt geïllustreerd hoe prijzen fluctueren zonder een voorspelbaar pad.
Wiskunde
In de zuivere wiskunde bieden willekeurige wandelingen oplossingen voor complexe problemen. Ze zijn bijvoorbeeld nuttig bij het oplossen van de vergelijking van Laplace, het analyseren van netwerken en het verkennen van combinatoriek.
Natuurkunde en chemie
In de natuurwetenschappen zijn willekeurige wandelingen cruciaal voor het modelleren van diffusieprocessen, zoals de manier waarop moleculen zich door een medium verspreiden. Brownse beweging, waarbij de deeltjes die in een vloeistof zijn gesuspendeerd onvoorspelbaar bewegen door botsingen met omringende moleculen, is een klassiek voorbeeld dat nauwkeurig kan worden gesimuleerd met behulp van willekeurige wandelingen. Dit is eigenlijk hoe ik voor het eerst over willekeurige wandelingen leerde.
Biologie
Willekeurige wandelingen zijn waardevol in de ecologie voor het bestuderen van dierenbewegingen. Dieren die op zoek zijn naar hulpbronnen lijken soms een willekeurige wandeling te maken, soms bevooroordeeld naar gebieden met bekende hulpbronnen. Andere biologische concepten, zoals de verspreiding van populaties of genen, kunnen vaak gemodelleerd worden met principes van willekeurige wandelingen, wat het gemakkelijker maakt om veranderingen binnen ecosystemen te begrijpen en te voorspellen.
Bijzondere gevallen en varianten van willekeurige wandelingen
Naast de klassieke willekeurige wandeling zijn er verschillende geavanceerde varianten die het concept uitbreiden voor gespecialiseerde toepassingen.
Zichzelf ontwijkende wandelingen
Een zichzelf ontwijkende wandeling is een willekeurige wandeling waarin het pad geen enkele positie herbezoekt die het al is gepasseerd. Deze variant is bijzonder nuttig in gebieden zoals de polymeerchemie, waar het kan modelleren hoe polymeerketens zich vormen zonder zichzelf te kruisen. Omdat elke stap eerder bezochte punten vermijdt, zijn zichzelf ontwijkende wandelingen meer beperkt dan traditionele willekeurige wandelingen. Dit betekent dat ze computationeel uitdagend zijn, maar nuttig voor het begrijpen van niet-overlappende paden in beperkte ruimtes.
Vertakking
Bij vertakkende willekeurige wandelingen kan het pad zich opsplitsen in meerdere takken, waarbij elke tak een willekeurige wandeling volgt. Dit type wandeling is essentieel bij het modelleren van vertakkingsprocessen zoals celverdeling of de verspreiding van informatie door netwerken. Elke “tak” vertegenwoordigt een onafhankelijk willekeurig pad dat afkomstig is van een gemeenschappelijke bron.
Correlerende wandelingen
Correlerende wandelingen gaan nog een stap verder, waarbij de richting van elke stap gedeeltelijk wordt beïnvloed door de vorige stap. Deze variant is nuttig voor het modelleren van traagheid in systemen waar veranderingen geleidelijk plaatsvinden in plaats van willekeurig. Correlerende wandelingen worden vaak toegepast in de financiële sector om prijstrends te simuleren of in bewegingsecologie om te begrijpen hoe dieren zich in hun omgeving verplaatsen met enige herinnering aan hun vorige richting.
Loop-gewiste wandelingen
Een loop-gewiste wandeling is een variant waarbij lussen, of paden die zichzelf kruisen, worden verwijderd zodra ze worden gevormd. Elke keer dat een stap een positie opnieuw bezoekt, wordt de tussenliggende lus gewist, waardoor een gestroomlijnd, niet-herhalend pad overblijft. Loop-gewiste wandelingen worden veel toegepast in netwerkanalyse en doolhofgeneratie-algoritmes omdat ze paden creëren die redundantie vermijden.
Random Walks Implementeren in Python
Laten we proberen een random walk in Python te implementeren.Om te beginnen, zorg ervoor dat je Python hebt geïnstalleerd (we gebruiken Python 3.10) en de benodigde bibliotheken beschikbaar zijn. Je kunt eventuele ontbrekende bibliotheken installeren met pip. Dit is wat we zullen gebruiken:
import numpy as np # voor numerieke operaties en het genereren van willekeurige stappen import matplotlib.pyplot as plt # voor het plotten en visualiseren van de random walks
1D random walk
We beginnen met een eenvoudige eendimensionale random walk, waarbij elke stap ofwel +1 of -1 is, willekeurig gekozen.
# Parameters n_steps = 100 # Aantal stappen # Genereer willekeurige stappen: +1 of -1 steps = np.random.choice([-1, 1], size=n_steps) # Bereken posities positions = np.cumsum(steps) # Plot de random walk plt.figure(figsize=(10, 6)) plt.plot(positions, marker='o', linestyle='-', markersize=4) plt.title("1D Random Walk") plt.xlabel("Step") plt.ylabel("Position") plt.grid(True) plt.show()
Dit genereert een eenvoudige willekeurige wandeling en visualiseert de voortgang in de loop van de tijd. Hier is de output wanneer ik deze code uitvoer:
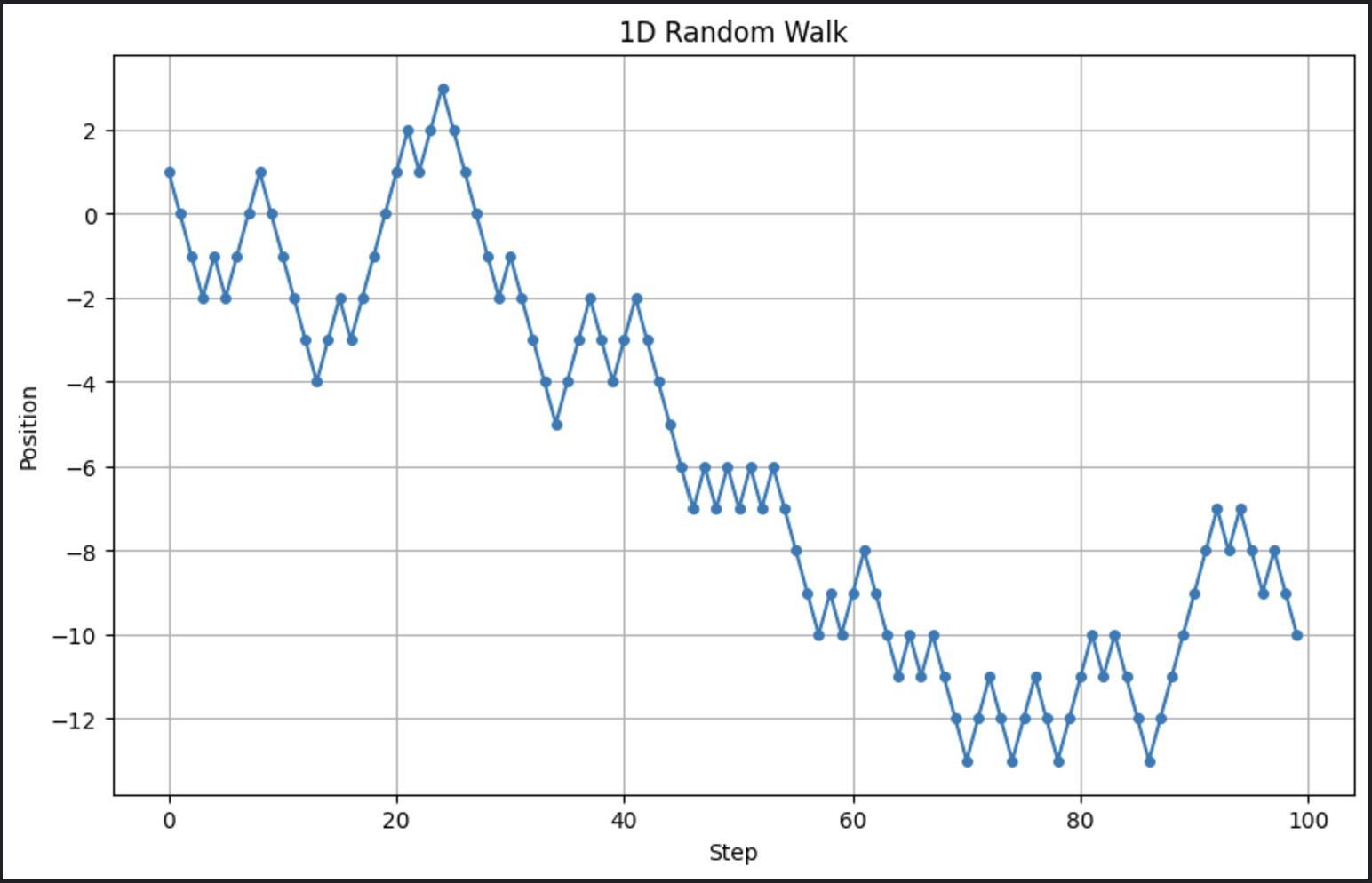
Onthoud, we draaien een stochastisch model. Dit betekent dat elke keer dat we het uitvoeren, de output er een beetje anders uit zal zien.
2D willekeurige wandeling
Laten we nu de willekeurige wandeling uitbreiden naar twee dimensies. Bij elke stap wordt de richting willekeurig gekozen.
# Parameters n_steps = 500 # Genereer willekeurige stappen in de x- en y-richtingen x_steps = np.random.choice([-1, 1], size=n_steps) y_steps = np.random.choice([-1, 1], size=n_steps) # Bereken posities x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Plot de 2D willekeurige wandeling plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Rode stip voor start plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Zwarte stip voor eind plt.title("2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Zorgt voor gelijke schaalverdeling voor beide assen plt.legend() plt.show()
Deze code creëert een visueel aantrekkelijke pad in twee dimensies.
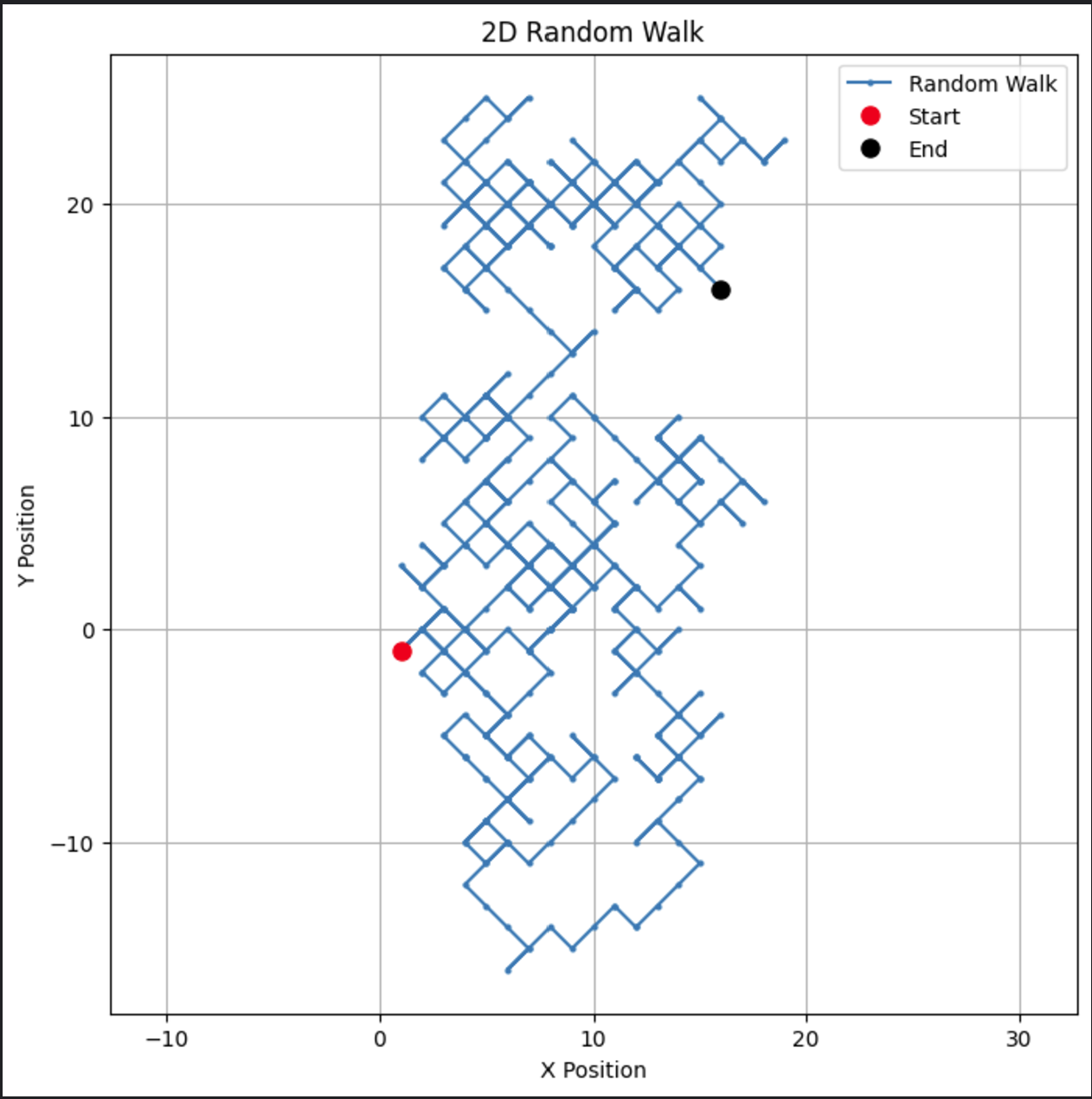
Dit type van tweedimensionale willekeurige wandeling kan worden aangepast voor toepassingen zoals de beweging van deeltjes of ruimtelijke modellering.
Vooringenomen willekeurige wandeling
Laten we ten slotte kijken naar een iets complexer voorbeeld: een vooringenomen willekeurige wandeling. Om vooringenomenheid in te voeren, kunnen we de kansen van elke staprichting aanpassen. Bijvoorbeeld, we zouden omhoog stappen waarschijnlijker kunnen maken.
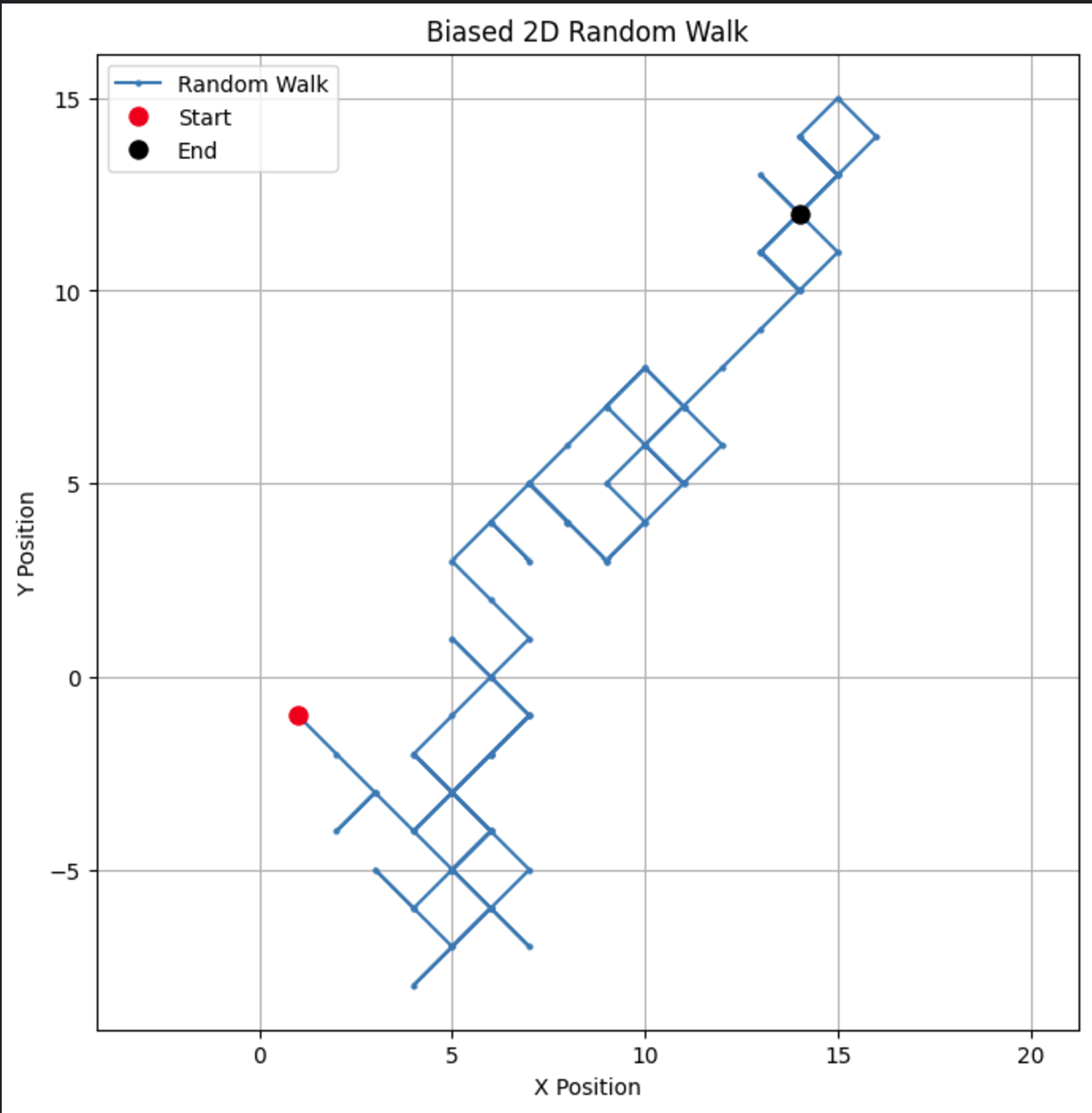
# Parameters n_steps = 100 bias = 0.7 # Kans om +1 te stappen # Genereer vooringenomen willekeurige stappen in de x- en y-richting x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) # Bereken posities x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Plot de vooringenomen 2D willekeurige wandeling plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Rode stip voor start plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Zwarte stip voor einde plt.title("Biased 2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Zorgt voor gelijke schaalverdeling voor beide assen plt.legend() plt.show()
Door de bias te veranderen, kun je observeren hoe de wandeling een bepaalde richting lijkt te begunstigen, wat real-world scenario’s simuleert zoals drift in aandelenkoersen of dierenmigratiepatronen.
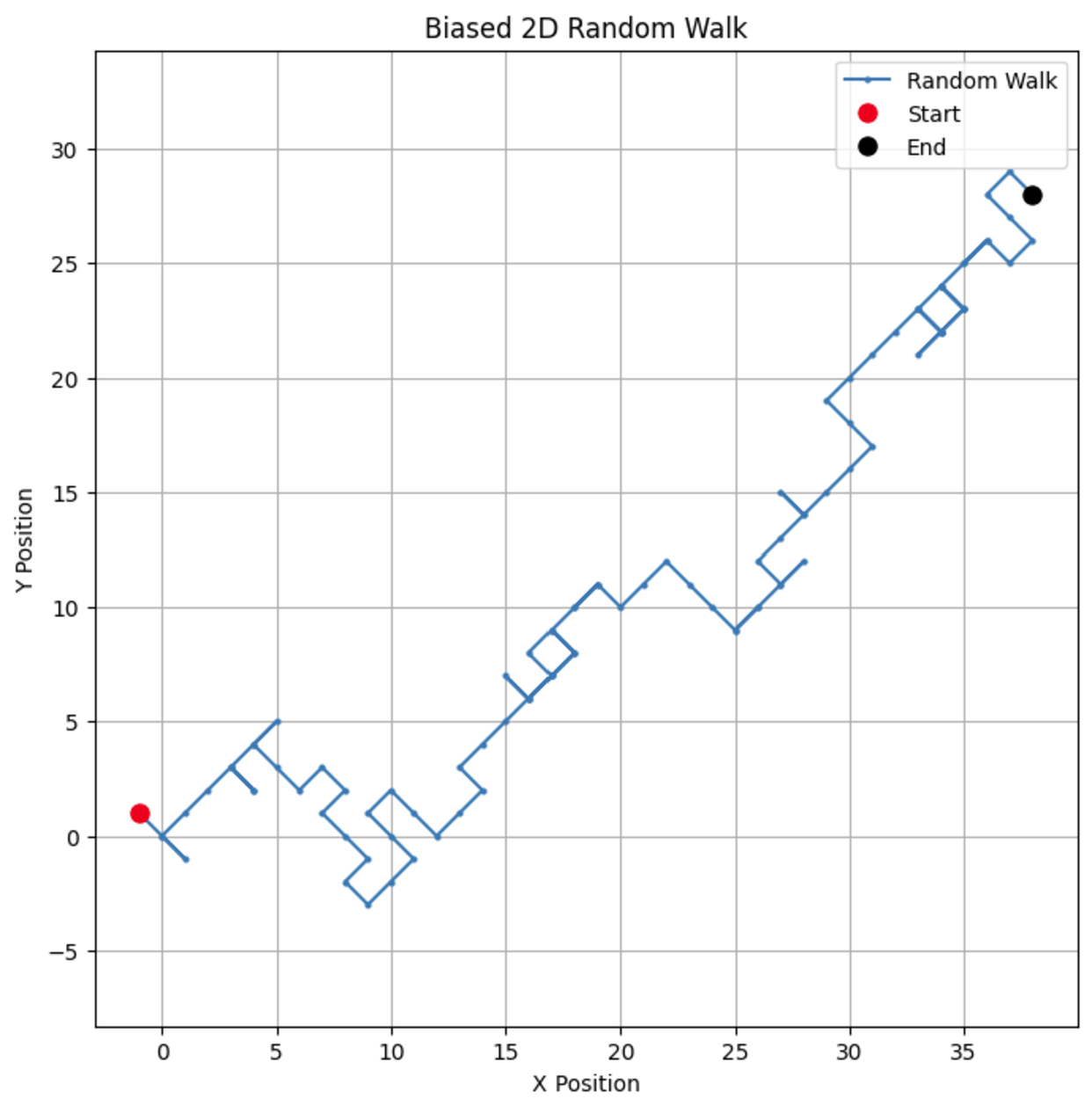
Als we de bias parameter veranderen naar 0.55, kunnen we een dramatisch verschil zien in hoe het model zich gedraagt. Hoewel het nog steeds een voorkeur heeft om omhoog te gaan, is de bias niet zo sterk, wat leidt tot meer lussen en omwegen.
Conclusie
Willekeurige wandelingen zijn een waardevol modelleringsinstrument voor datawetenschappers, toepasbaar in vakgebieden van natuurkunde tot financiën en verder. Hun vermogen om complexe, stochastische processen te modelleren maakt ze onmisbaar in veel real-world scenario’s.
Zin in meer? Bekijk de reeks kans- en statistiekcursussen van DataCamp. Je vindt allerlei geweldige cursussen in zowel Python als R. Als je geïnteresseerd bent in meer geavanceerde inhoud, bekijk dan de cursus van DataCamp over Statistische Simulatie in Python en de zelfstudie Inleiding tot Machine Learning. Of als je klaar bent om je kennis te testen, probeer dan een aantal van deze kanspuzzels.













