الخطوة بالخطوة: استكشاف نموذج المشي العشوائي

في دورتي الأولى التي تتضمن البرمجة في مجال الإحصاءات في الجامعة، قدم معلمي سؤالًا: كيف يمكننا نمذجة حركة براونية لجسيم حبيبات واحد في صحن ماء؟ بعد عدة محاولات خاطئة، تعثرت أنا وزملائي في النهاية على الإجابة الصحيحة: مسار عشوائي. فيما بعد تعلمت أن هذا النموذج البسيط يُستخدم لنمذجة أنواع مختلفة من الأشياء، بدءًا من حركة الحيوانات إلى تقلبات أسعار الأسهم.

في هذا المقال، سنستكشف الأسس الرياضية للمسارات العشوائية، وندرس أنواعًا مختلفة، ونناقش تطبيقاتها. جزء مما يجعل المسار العشوائي مثيرًا للاهتمام هو استخدامه في العديد من التخصصات المختلفة. بالإضافة إلى مثالي، في الفيزياء، يساعد في وصف حركة الجسيمات؛ في المالية، يُنمذج تقلبات أسعار الأسهم؛ وفي علم الأحياء، يشرح أنماط حركة الحيوانات. تلتقط المسارات العشوائية العشوائية الحقيقية، وهو أمر أساسي لمحاكاة العمليات العشوائية.

لأولئك الذين يبحثون عن بناء أسس قوية في الإحصاءات التي تدعم نظرية المشي العشوائي، نوصي بالبدء مع دورة مقدمة إلى الإحصاء في R أو دورة مقدمة إلى الإحصاء في Python.

ما هي المشي العشوائي؟

في نظرية الاحتمالات، المشي العشوائي هو نموذج يصف سلسلة من الخطوات العشوائية التي تشكل مسارًا. أو بمعنى آخر، يمكننا القول إن المشي العشوائي هو نموذج رياضي يصف مسارًا يتكون من سلسلة من الخطوات، حيث يتم تحديد كل خطوة بشكل مستقل وباحتمال معين. هذه العشوائية تجعل المشي العشوائي غير قابل للتنبؤ.

تخيل شخصًا يأخذ خطوة في اتجاه عشوائي في كل لحظة. مع مرور الوقت، يتكون مسارهم من درب غير قابل للتنبؤ. على الرغم من بساطته، فإن هذا المفهوم يحمل عمقًا وقدرة مدهشة، حيث يمكنه تمثيل سيناريوهات حقيقية مختلفة تشمل العشوائية.

شرح مفاهيمي للتجول العشوائي. الصورة مأخوذة برخصة من napkin.ai.

تعود فكرة التجول العشوائي إلى دراسات الاحتمالات البدائية. أحد أقدم الأمثلة، يُسمى في كثير من الأحيان بتجول المُخمور، يوضح كيف يتجول الشخص عشوائيًا بدلاً من التحرك بشكل قابل للتنبؤ نحو وجهته. هذا العشوائية، بالاقتران مع افتراض أن كل خطوة مستقلة عن السابقة، وضعت أسس نماذج التجول العشوائي الحديثة.

فهم رياضيات التجول العشوائي

لفهم التجول العشوائي، دعنا نبدأ بحالة بسيطة: تجول عشوائي أحادي البُعد (1D).تخيل جسيمًا على خط أعداد. يمكنه التحرك إما +1 أو -1 على طول الخط مع كل خطوة. يُحدد كل حركة بانحياز متساوي لليمين أو اليسار. مع مرور الوقت، تشكل موقع الجسيم توزيع احتمالي يتفرع، يمثل احتمالية العثور عليه في مواقع مختلفة.

يمكن توسيع هذا المبدأ إلى بعدين أو ثلاثة أبعاد. في المشي العشوائي ثنائي الأبعاد (2D)، يتحرك الجسيم على مستوى ويمكنه الخطو في أي من الاتجاهات الأربعة الرئيسية (أعلى، أسفل، يسار، يمين) بنفس الاحتمال. بالمثل، في المشي العشوائي ثلاثي الأبعاد (3D)، يتحرك الجسيم في الفضاء ويمكنه الخطو في أي من الاتجاهات الستة الممكنة (أعلى، أسفل، يسار، يمين، إلى الأمام، إلى الوراء) بنفس الاحتمال. تلتقط هذه المشيات العشوائية ذات الأبعاد الأعلى سيناريوهات أكثر تعقيدًا وواقعية.

ميزة تعريفية للمشيات العشوائية هي طبيعتها العشوائية، مما يعني أن كل خطوة تعتمد فقط على الوضع الحالي وليس على الخطوات السابقة. يجعل ذلك منها نوعًا من العملية ماركوف – مفهوم رياضي حيث يعتمد الحالة المستقبلية فقط على الحالة الحالية، وليس على تسلسل الأحداث التي سبقتها. هذه الحركة “بلا ذاكرة”، بالاشتراك مع توزيعات الاحتمال التي تصف المواقع المحتملة، توفر أساسًا رياضيًا قويًا لفهم المشيات العشوائية.

يمكننا تحليل المشي العشوائي باستخدام الخصائص الإحصائية لفهم سلوكه مع مرور الوقت. يتضمن ذلك فحص جوانب مثل المسافة المتوقعة من نقطة البداية، وتوزيع الاحتمالات للمواقع المحتملة، واحتمالية العودة إلى الأصل. تساعدنا هذه التحليلات على قياس العشوائية والقابلية للتنبؤ، وتوفير رؤى حول الأنماط، وإجراء التنبؤات.

الخصائص الرئيسية للمشي العشوائي

يمتلك المشي العشوائي العديد من الخصائص المهمة التي تساعدنا على فهم سلوكه وتطبيقاته. إليك بعض الجوانب الرئيسية التي يجب مراعاتها:

التوقع والتباين

في المشي العشوائي أحادي الأبعاد، يمكننا حساب المسافة المتوقعة (أو الموقع المتوسط) من نقطة البداية مع مرور الوقت. إذا كانت لكل خطوة احتمالية متساوية للتحرك يسارًا أو يمينًا، فإن الموقع المتوقع بعد العديد من الخطوات يبقى صفرًا، مما يعني أنه، في المتوسط، يبقى المتنقل بالقرب من نقطة البداية.

ومع ذلك، فإن تباين الموقع، الذي يقيس مدى انتشار أو تشتت المواقع المحتملة، يزداد مع كل خطوة. بشكل محدد، في المشي العشوائي المتناظر، ينمو التباين بشكل خطي مع عدد الخطوات، مما يجعله مؤشراً مفيداً على المسافة النموذجية من الأصل مع مرور الوقت.

الارتباط الذاتي

بينما لا توجد علاقة بين الخطوات في المشي العشوائي البسيط (كل خطوة مستقلة عن السابقة)، فإن بعض أنواع المشي العشوائي تقدم ارتباطاً ذاتياً، حيث يمكن أن تؤثر الخطوات السابقة على الخطوات المستقبلية. على سبيل المثال، في المشي العشوائي المنحاز، قد تميل الخطوات قليلاً في اتجاه واحد، مما يجعل المواقع أكثر قابلية للتنبؤ.

يؤثر الارتباط الذاتي في المشي العشوائي على كيفية نمذجة وتوقع تقدم المشي. هذا مهم بشكل خاص في التطبيقات التي يؤثر فيها السلوك السابق على الخطوات المستقبلية، مثل بعض النماذج المالية.

نظرية الحد المركزي

يخبرنا مبرهنة الحد المركزي (CLT) بأن مجموع عدد كبير من المتغيرات العشوائية المستقلة تميل إلى اتباع توزيعًا طبيعيًا (أو غاوسيًا)، بغض النظر عن التوزيع الأصلي. في سياق السير العشوائية، يعني ذلك أنه مع زيادة عدد الخطوات، يميل توزيع المواقع إلى أن يشبه توزيعًا طبيعيًا. هذه خاصية مفيدة لأنها تسمح لنا بتقريب احتمالية العثور على الماشي في بعض المسافات عن نقطة البداية.

قانون الأعداد الكبيرة

قانون الأعداد الكبيرة (LLN) يشرح أن مع زيادة عدد التجارب أو الخطوات، يتقارب متوسط النتائج نحو المتوسط الحقيقي. بالنسبة للسير العشوائية، يعني ذلك أنه في حين تبقى الموقف المتوسط صفرًا، فإن الانحراف المعياري ونطاق المواقف الممكنة ينموان بشكل قابل للتنبؤ مع كل خطوة إضافية. يساعد هذا المبدأ على تقليل الفجوة بين العشوائية النقية والأنماط الإحصائية القابلة للتنبؤ في العينات الكبيرة.

أنواع السير العشوائية

المشيات العشوائية تختلف بشكل واسع اعتمادًا على القواعد التي تحكم كل خطوة. هذه الأنواع تؤثر على سلوك المشي. تم تصميم بعضها للبيئات البسيطة أو المنظمة بينما يتم تجهيز البعض الآخر لظواهر العالم الحقيقي الأكثر تعقيدًا. دعونا نستكشف بعض أنواع المشي العشوائي الأكثر شيوعًا.

المشي العشوائي في الأبعاد 1D و 2D و 3D

تلعب الأبعاد دورًا أساسيًا في سلوك المشي العشوائي. في المشي العشوائي ثنائي الأبعاد، تزداد الطرق الممكنة بشكل كبير، مما يدخل سلوكًا جديدًا. على سبيل المثال، في المشي العشوائي ثنائي الأبعاد، تبقى احتمالية العودة إلى نقطة البداية مرتفعة، بينما في المشي العشوائي ثلاثي الأبعاد، تقل هذه الاحتمالية.

ومع ذلك، بمجرد التحرك إلى المشي العشوائي في الأبعاد 2D (المستوى) و 3D (الفضاء)، يزداد عدد المسارات الممكنة بشكل كبير، مما يدخل سلوكًا جديدًا. على سبيل المثال، في المشي العشوائي ثنائي الأبعاد، تبقى احتمالية العودة إلى نقطة البداية مرتفعة، بينما في المشي العشوائي ثلاثي الأبعاد، تقل هذه الاحتمالية.

هذا التغيير مهم في مجالات مثل الفيزياء والكيمياء، حيث قد تنتشر الجسيمات بشكل مختلف اعتمادًا على القيود البُعدية.

المشي العشوائي على الشبكة

في المشي العشوائي على الشبكة، يتم حصر الحركة في نقاط منفصلة على شبكة أو مصفوفة. يُستخدم هذا النوع من المشي بشكل شائع في الفيزياء ونظرية الشبكات، حيث يتم ترتيب العقد في شبكة، ولا يمكن أن تحدث الحركة إلا إلى العقد المجاورة.

مثال شائع هو شبكة ثنائية الأبعاد، حيث يسمح كل خطوة بالحركة إلى نقاط مجاورة على شبكة كارتيسية. تُبسط هذه القيود النمذجة من خلال تقليل مسارات الحركة، وهو مفيد عند محاكاة الشبكات المعقدة أو الهياكل الجزيئية.

المشي العشوائي الغاوسي

في السير العشوائي الجاوسي، يتم تحديد حجم كل خطوة بواسطة توزيع جاوسي (أو طبيعي). بدلاً من التحرك بمسافة ثابتة، يتغير حجم الخطوة وفقًا لتوزيع منحنى الجرس، حيث تكون معظم الخطوات صغيرة وتحدث قفزات كبيرة أحيانًا. يُستخدم هذا النوع من السير بشكل متكرر في النمذجة المالية لمراعاة التقلبات في تغيرات أسعار الأصول.

السير العشوائي غير المتجانس والمتحيز

السير العشوائي غير المتجانس والمتحيز يسمح بتغيير اتجاه الخطوة وحجمها استنادًا إلى احتمالات معينة. تجعل هذه المرونة هذه الأنواع أكثر قابلية للتكيف مع السيناريوهات الحقيقية.

في السير العشوائي غير المتجانس، قد تتغير احتمالية التحرك في أي اتجاه استنادًا إلى الموقع أو الظروف الخارجية. على سبيل المثال، قد تميل الحيوانات التي تبحث عن الطعام نحو المناطق التي تحتوي على موارد معروفة، مما يخلق سيرًا عشوائيًا متحيزًا. يُستخدم هذا النوع من السير لدراسة السلوكيات التي تعتمد على عوامل السياق.

السير العشوائي بانجراف

في المشي العشوائي مع الانجراف, هناك اتجاه ثابت للحركة في اتجاه واحد. على سبيل المثال, قد تظهر أسعار الأسهم اتجاهًا عامًا صعوديًا مع مرور الوقت على الرغم من التقلبات اليومية. الانجراف في هذه المشيات يمثل قوة خارجية أو اتجاه يؤثر على المسار. يُرى هذا النوع في كثير من الأحيان في المالية, حيث تدمج النماذج مصطلح الانجراف لتمثيل النمو أو الانخفاض, مما يوفر نهجًا أكثر واقعية لتوقع أسعار الأصول واتجاهات السوق.

كل نوع من هذه المشيات العشوائية يخدم غرضًا فريدًا, يقدم طرقًا مختلفة لنمذجة السلوك العشوائي, ولكن المنظم. قيود الأبعاد, توزيع الخطوات, ووجود الانجراف أو التحيز تجعل المشيات العشوائية مرنة للغاية لنمذجة البيانات والمحاكاة عبر المجالات.

تطبيقات العالم الحقيقي للمشيات العشوائية

المشيات العشوائية ليست مجرد بنى نظرية, بل تلعب دورًا أساسيًا في العديد من التطبيقات العملية عبر التخصصات. دعونا نستكشف كيف تُسهم المشيات العشوائية في حل المشاكل العملية في مختلف القطاعات.

التطبيقات في علوم البيانات وتعلم الآلة

علوم الحاسوب

المشيات العشوائية تمثل أساس عدة خوارزميات في علم الحاسوب، مثل عينات عشوائية، عبور الرسوم البيانية على الويب، وتقسيم الصور. على سبيل المثال، استخدم خوارزمية PageRank التابعة لشركة Google المشيات العشوائية لتصنيف صفحات الويب استنادًا إلى صلتها بالموضوع، محاكاة لكيفية تصفح المستخدم بشكل عشوائي بين الروابط على الإنترنت.

استخراج السمات

في تعلم الآلة، يمكن للمشيات العشوائية مساعدة في استخراج السمات عن طريق تسليط الضوء على العلاقات بين نقاط البيانات. على سبيل المثال، في تحليل الشبكات، يمكن للمشيات العشوائية كشف التجمعات أو المجتمعات، مما يساعد في المهام مثل أنظمة التوصيات وتحليل الشبكات الاجتماعية.

كشف الشواذ

يمكن أيضًا استخدام المشيات العشوائية لاكتشاف الشواذ في مجموعات البيانات. على سبيل المثال، إذا انحرفت نقاط البيانات بشكل كبير عن المسار النموذجي في نموذج المشي العشوائي، فقد تشير هذه النقاط إلى أحداث غير عادية أو أخطاء في البيانات. يكون كشف الشواذ قيمة خاصة خاصة في مجالات مثل أمن المعلومات واكتشاف الاحتيال.

محاكاة العمليات الاحتمالية

المشيات العشوائية تحاكي العمليات العشوائية أو المحددة بشكل عشوائي، مما يتيح لعلماء البيانات نمذجة الظواهر العالمية غير المتنبئ بها. من خلال محاكاة المشيات العشوائية، يمكننا الحصول على رؤى حول الأنظمة التي تعتبر التنبؤ الدقيق فيها تحديًا، مثل أنماط الطقس أو سلوك العملاء.

التنبؤ بسلاسل الزمن

في تحليل سلاسل الزمن، تشكل المشيات العشوائية أساسًا لبعض النماذج التنبؤية، بما في ذلك فرضية المشي العشوائي في المالية. تفترض هذه النماذج أن القيم المستقبلية في سلسلة زمنية تعتمد فقط على القيمة الأخيرة، دون أي ارتباط بالاتجاهات السابقة.لمزيد من المعلومات حول التنبؤ بسلاسل الزمن، تحقق من ARIMA لتوقعات سلاسل الزمن: دليل شامل. كما يمكنك أخذ دورتنا التنبؤ في R مع البروفيسور هيندمان، الذي يربط نماذج المشي العشوائي بأساليب التنبؤ الساذجة والساذجة الموسمية.

التطبيقات في مجالات أخرى

المالية

واحدة من أبرز استخدامات المشيات العشوائية هي في النمذجة المالية، خاصةً لتوقع أسعار الأسهم. فرضية السوق الفعال تقترح أن حركات أسعار الأسهم هي عمومًا عشوائية، حيث يتم استيعاب المعلومات الجديدة على الفور، مما يجعل الأسعار المستقبلية غير قابلة للتنبؤ. يمكن استخدام المشيات العشوائية لنمذجة تغييرات أسعار الأسهم مع مرور الوقت، موضحة كيفية تذبذب الأسعار دون مسار قابل للتنبؤ.

الرياضيات

في الرياضيات النقية، توفر المشيات العشوائية حلاً للمشاكل المعقدة. على سبيل المثال، فهي مفيدة في حل معادلة لابلاس، وتحليل الشبكات، واستكشاف العددية.

الفيزياء والكيمياء

في العلوم الطبيعية، تعتبر المشيات العشوائية أمرًا حاسمًا لنمذجة عمليات الانتشار، مثل الطريقة التي تنتشر بها الجزيئات من خلال وسط معين. الحركة البراونية، حيث تتحرك الجسيمات المعلقة في سائل بشكل عشوائي بسبب التصادم مع الجزيئات المحيطة، هي مثال كلاسيكي يمكن محاكاته بدقة باستخدام المشيات العشوائية. هذا هو بالفعل كيف تعلمت عن المشيات العشوائية أول مرة.

علم الأحياء

المشي العشوائي له قيمة في علم البيئة لدراسة أنماط حركة الحيوانات. قد يبدو أن الحيوانات التي تبحث عن الموارد تتحرك في مسار عشوائي، أحيانًا ما تميل نحو المناطق التي تحتوي على موارد معروفة. يمكن أيضًا نمذجة مفاهيم بيولوجية أخرى، مثل انتشار السكان أو الجينات، غالبًا باستخدام مبادئ المشي العشوائي، مما يسهل فهم وتوقع التغيرات داخل النظم البيئية.

حالات خاصة ومتغيرات المشي العشوائي

بالإضافة إلى المشي العشوائي الكلاسيكي، هناك العديد من المتغيرات المتقدمة التي توسع المفهوم ليتناسب مع التطبيقات المتخصصة.

المشي الذاتي التجنب

المشي الذاتي التجنب هو مشي عشوائي حيث لا تعيد المسار زيارة أي موضع قد مر به سابقًا. هذه المتغير مفيد بشكل خاص في مجالات مثل كيمياء البوليمرات، حيث يمكنه نمذجة كيفية تشكيل سلاسل البوليمر دون أن تتقاطع مع نفسها. نظرًا لأن كل خطوة تتجنب النقاط التي تمت زيارتها مسبقًا، فإن المشي الذاتي التجنب يكون أكثر تقييدًا من المشي العشوائي التقليدي. وهذا يعني أنه يمثل تحديًا حسابيًا ولكنه مفيد لفهم المسارات غير المتداخلة في المساحات المغلقة.

التفرع

في المشيات العشوائية الفرعية، يمكن أن ينقسم المسار إلى فروع متعددة، حيث يتبع كل فرع مشيًا عشوائيًا. هذا النوع من المشيات مهم في نمذجة العمليات الفرعية مثل تقسيم الخلايا أو انتشار المعلومات عبر الشبكات. كل “فرع” يمثل مسارًا عشوائيًا مستقل ينبع من مصدر مشترك.

المشيات المترابطة

تأخذ المشيات المترابطة هذا المفهوم خطوة إضافية، حيث يتأثر اتجاه كل خطوة جزئيًا بالخطوة السابقة. هذا النوع مفيد في نمذجة اللزوجة في الأنظمة حيث تحدث التغييرات تدريجيًا بدلاً من عشوائيًا. وتُطبق المشيات المترابطة في العديد من المجالات مثل الشؤون المالية لمحاكاة اتجاهات الأسعار أو في علم الحركة البيئية لفهم كيفية توجيه الحيوانات بيئتها بذاكرة بعض اتجاهات ماضيها.

المشيات المحذوفة الحلقيًا

المشيات المحذوفة الحلقيًا هي نوع يتم فيه إزالة الحلقات، أو المسارات التي تعبر عن نفسها، كلما تكونت. كلما عادت الخطوة لموضع معين، يتم محو الحلقة الوسيطة، مما يترك مسارًا مبسطًا وغير مُكرر. وتُطبق المشيات المحذوفة الحلقيًا عادة في تحليل الشبكات وخوارزميات إنشاء المتاهات لأنها تنشئ مسارات تتجنب التكرار.

تنفيذ المشي العشوائي في بايثون

دعنا نحاول تنفيذ مشي عشوائي في بايثون.للبدء، تأكد من تثبيت بايثون (سنستخدم بايثون 3.10) والمكتبات اللازمة. يمكنك تثبيت أي مكتبات مفقودة باستخدام pip. إليك ما سنستخدمه:

import numpy as np # للعمليات العددية وتوليد الخطوات العشوائية
import matplotlib.pyplot as plt # للرسم والتصور للمشي العشوائي

مشي عشوائي أحادي الأبعاد

سنبدأ بمشي عشوائي بسيط أحادي الأبعاد، حيث تكون كل خطوة إما +1 أو -1، يتم اختيارها عشوائيًا.

# المعلمات
n_steps = 100  # عدد الخطوات

# توليد خطوات عشوائية: +1 أو -1
steps = np.random.choice([-1, 1], size=n_steps)

# حساب المواقع
positions = np.cumsum(steps)

# رسم المشي العشوائي
plt.figure(figsize=(10, 6))
plt.plot(positions, marker='o', linestyle='-', markersize=4)
plt.title("1D Random Walk")
plt.xlabel("Step")
plt.ylabel("Position")
plt.grid(True)
plt.show()

هذا يولد مسار عشوائي بسيط ويصور التقدم على مر الزمن. إليك المخرجات عندما أشغل هذا الكود:

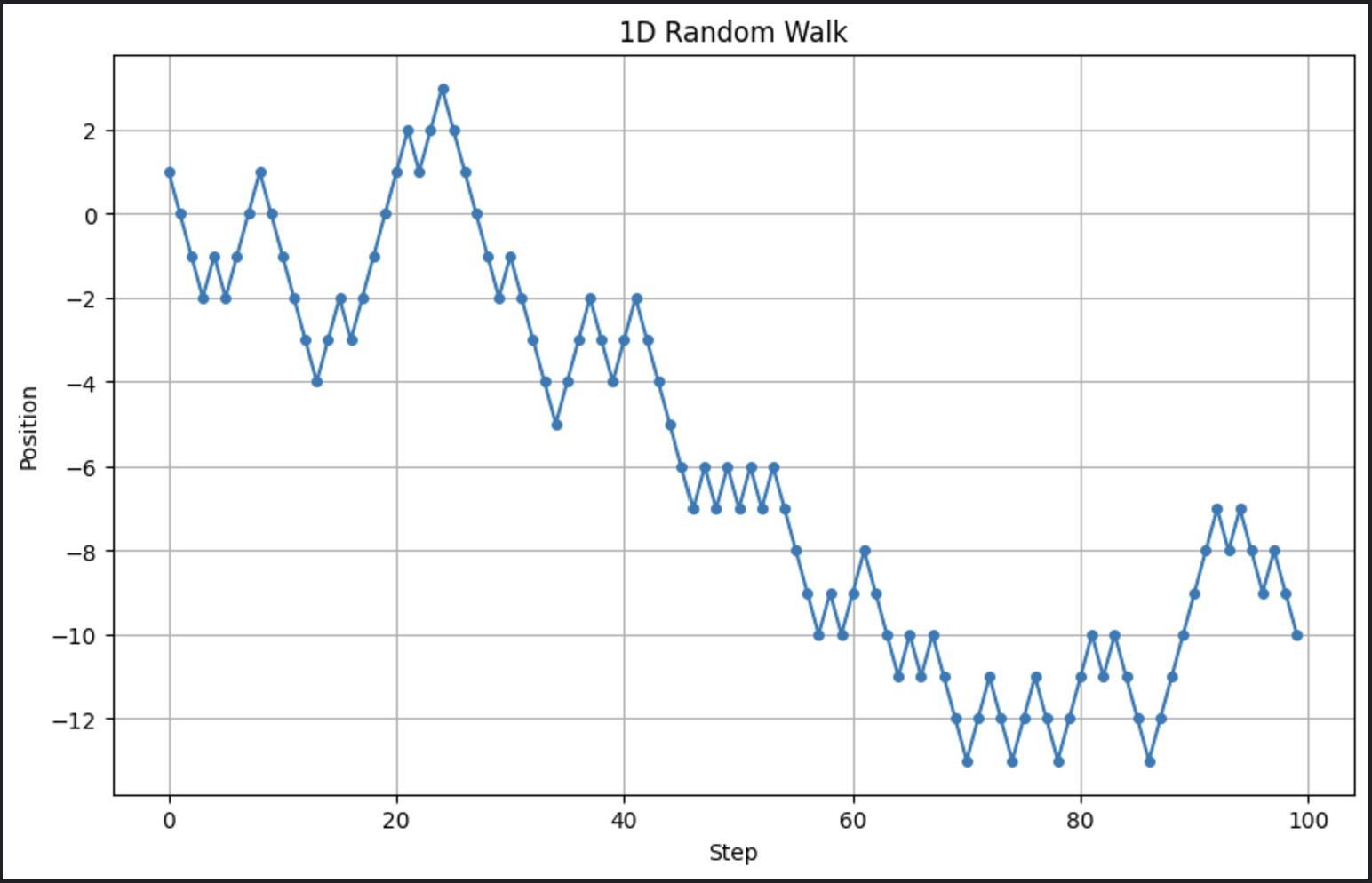
تذكر الآن أننا نشغل نموذجًا عشوائيًا. هذا يعني أنه في كل مرة نشغله، ستبدو المخرجات مختلفة قليلاً.

مسار عشوائي ثنائي الأبعاد

الآن دعنا نمدد المسار العشوائي إلى بعدين. في كل خطوة، سيتم اختيار الاتجاه بشكل عشوائي.

# المعلمات
n_steps = 500

# توليد خطوات عشوائية في اتجاهات x و y
x_steps = np.random.choice([-1, 1], size=n_steps)
y_steps = np.random.choice([-1, 1], size=n_steps)

# حساب المواقع
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# رسم المسار العشوائي ثنائي الأبعاد
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # نقطة حمراء للبداية
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # نقطة سوداء للنهاية
plt.title("2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # يضمن تكافؤ مقياس المحاور
plt.legend()
plt.show()

تُنشئ هذا الكود مسارًا جذابًا بصريًا في بعدين.

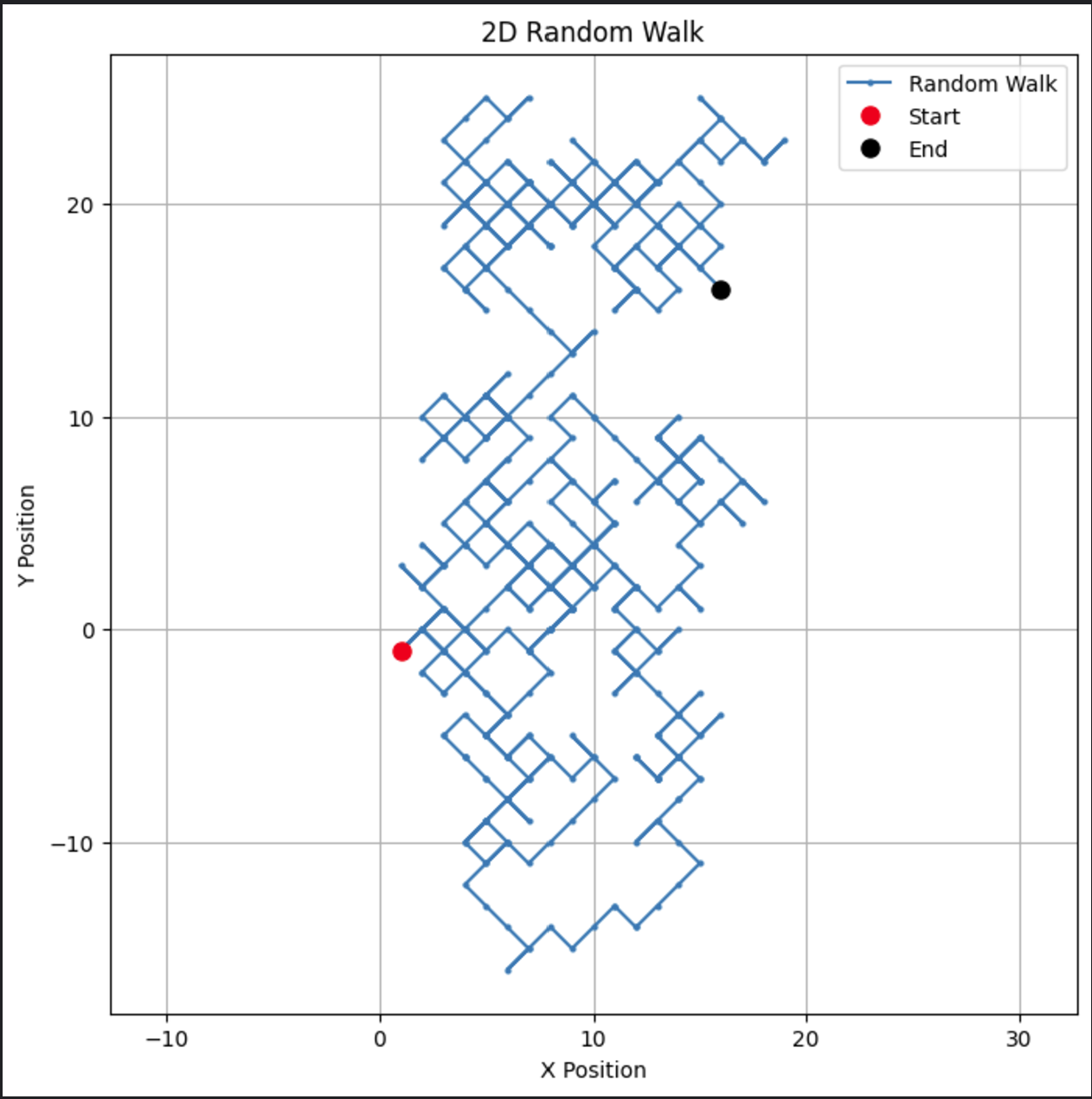
يمكن تعديل هذا النوع من المشي العشوائي ثنائي الأبعاد ليتناسب مع تطبيقات مثل حركة الجسيمات أو النمذجة المكانية.

المشي العشوائي المُحايد

أخيرًا، دعونا نلقي نظرة على مثال أكثر تعقيدًا قليلاً: مشي عشوائي مُحايد. لإدخال التحيز، يمكننا ضبط احتماليات كل اتجاه للخطوة. على سبيل المثال، قد نجعل الخطوات الصعودية أكثر احتمالية.

# المعلمات
n_steps = 100
bias = 0.7  # احتمالية الانتقال +1

# إنتاج خطوات عشوائية محايدة في اتجاهات x و y
x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])
y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])

# حساب المواقع
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# رسم المشي العشوائي ثنائي الأبعاد المحايد
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # نقطة حمراء للبداية
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # نقطة سوداء للنهاية
plt.title("Biased 2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # يضمن التوازن في مقياس الأبعاد المتساوي
plt.legend()
plt.show()

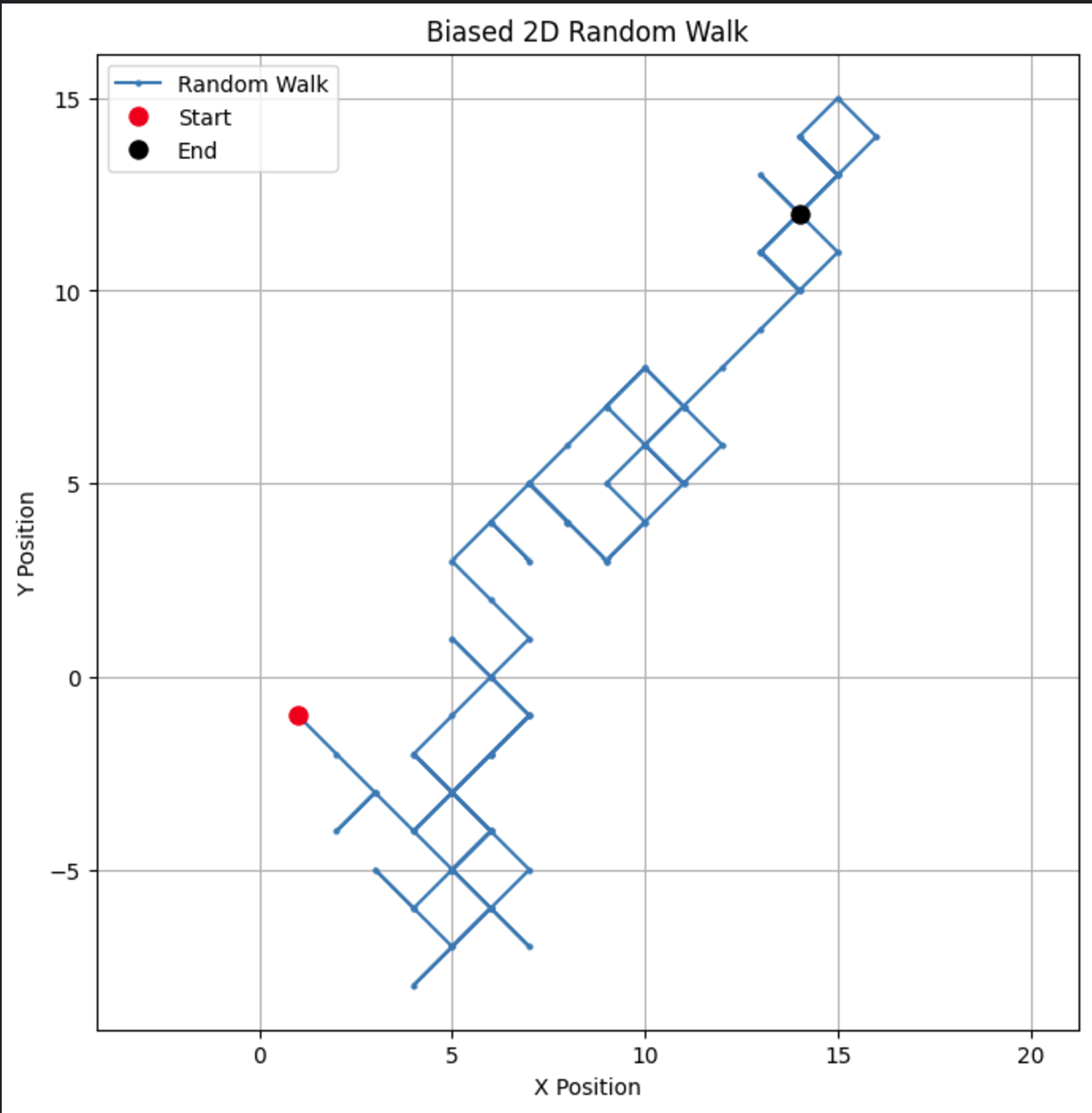
من خلال تغيير الانحياز، يمكنك ملاحظة كيف تميل المشي نحو اتجاه معين، محاكاة سيناريوهات العالم الحقيقي مثل الانجراف في أسعار الأسهم أو أنماط هجرة الحيوانات.

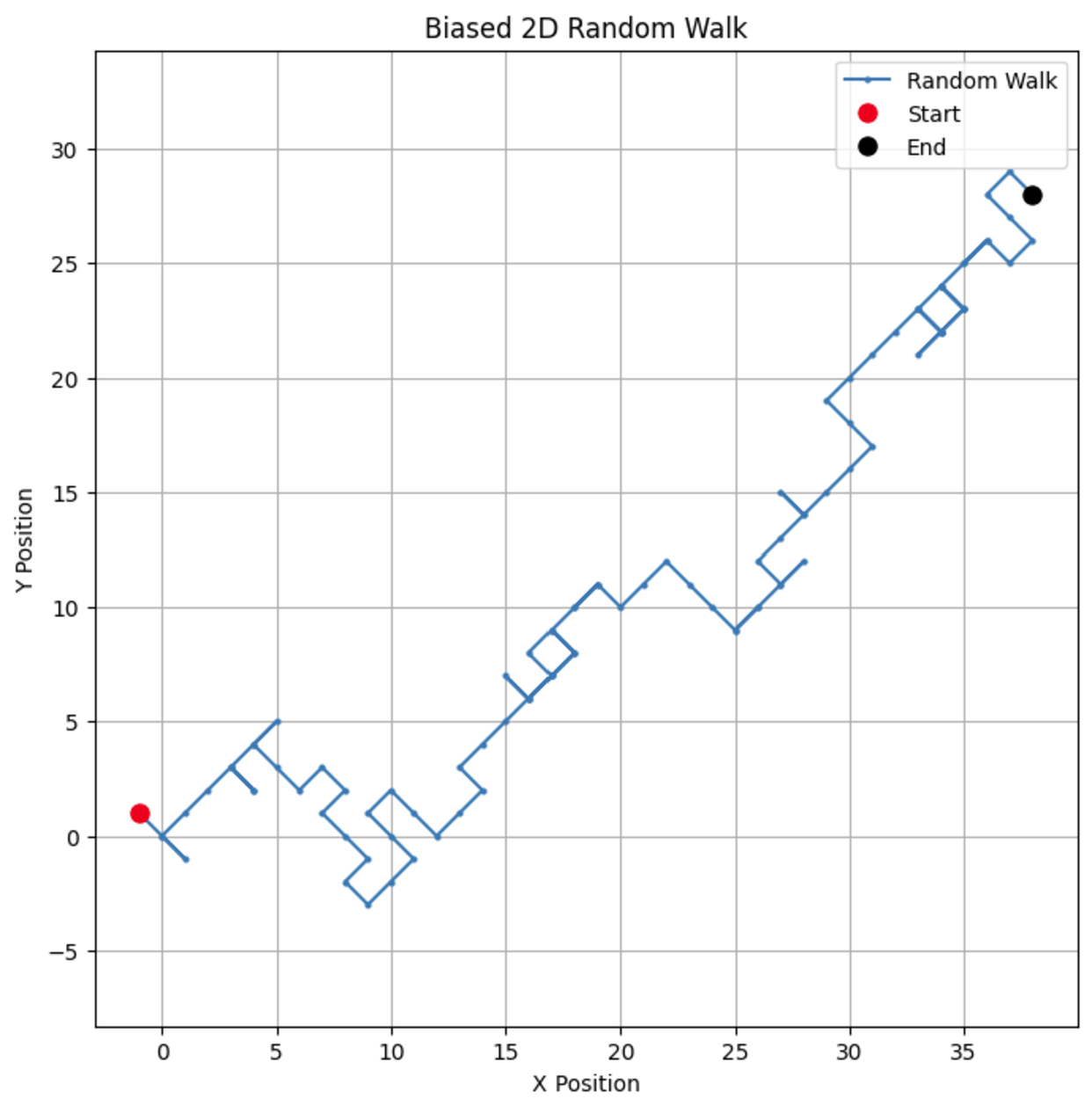
إذا قمنا بتغيير معلمة الانحياز إلى 0.55، يمكننا أن نرى فرقًا دراماتيكيًا في سلوك النموذج. بينما لا يزال لديه انحياز للارتفاع، إلا أن الانحياز ليس قويًا كما كان، مما يؤدي إلى مزيد من الدورات والتفافات.

الخاتمة

المشي العشوائي هو أداة نمذجة قيمة لعلماء البيانات، قابلة للتطبيق في مجالات تتراوح من الفيزياء إلى المالية وما بعدها. إن قدرتها على نمذجة العمليات المعقدة والعشوائية تجعلها لا غنى عنها في العديد من سيناريوهات العالم الحقيقي.

جائع للمزيد؟ تحقق من مجموعة DataCamp من دورات الاحتمالات والإحصاء. ستجد جميع أنواع الدورات الرائعة سواء في Python أو R. إذا كنت مهتمًا بالمحتوى المتقدم أكثر، تفقد دورة DataCamp عن المحاكاة الإحصائية في Python ودليل مقدمة في تعلم الآلة. أو إذا كنت جاهزًا لاختبار معرفتك، جرب بعض هذه ألغاز الاحتمالات.