In meinem ersten codierungsbasierten Statistikkurs an der Universität stellte mein Lehrer eine Frage: Wie können wir die Brownsche Bewegung eines einzelnen Pollenteilchens in einer Wasserschale modellieren? Nach mehreren fehlgeleiteten Versuchen stießen meine Mitschüler und ich schließlich auf die richtige Antwort: einen Zufallsspaziergang. Später erfuhr ich, dass dieses einfache Modell verwendet wird, um alle möglichen Dinge zu modellieren, von Tierbewegungen bis hin zu Schwankungen der Aktienkurse.
In diesem Artikel werden wir die mathematischen Grundlagen von Zufallsspaziergängen untersuchen, verschiedene Typen betrachten und ihre Anwendungen diskutieren. Ein Teil dessen, was den Zufallsspaziergang interessant macht, ist, dass er in so vielen verschiedenen Disziplinen verwendet wird. Neben meinem Beispiel hilft er in der Physik, die Bewegung von Teilchen zu beschreiben; in der Finanzwelt modelliert er Schwankungen der Aktienkurse; und in der Biologie erklärt er Bewegungsmuster von Tieren. Zufallsspaziergänge erfassen reale Zufälligkeit, was entscheidend ist für die Simulation stochastischer Prozesse.
Für diejenigen, die ein solides Fundament in den Statistiken aufbauen möchten, die der Random-Walk-Theorie zugrunde liegen, empfehlen wir, mit dem Kurs Einführung in die Statistik in R oder dem Kurs Einführung in die Statistik in Python zu beginnen.
Was sind Zufallswanderungen?
In der Wahrscheinlichkeitstheorie ist eine Zufallswanderung ein Modell, das eine Abfolge von zufälligen Schritten beschreibt, die einen Weg bilden. Oder anders ausgedrückt, könnte man sagen, dass eine Zufallswanderung ein mathematisches Modell ist, das einen Weg beschreibt, der durch eine Abfolge von Schritten gebildet wird, von denen jeder unabhängig und mit einer bestimmten Wahrscheinlichkeit bestimmt wird. Diese Stochastizität macht Zufallswanderungen grundsätzlich unvorhersehbar.
Stellen Sie sich eine Person vor, die in jedem Moment einen Schritt in eine zufällige Richtung macht. Im Laufe der Zeit bildet ihr Weg einen unvorhersehbaren, schlängelnden Pfad. Trotz seiner Einfachheit hat dieses Konzept erstaunliche Tiefe und Vielseitigkeit und modelliert verschiedene Szenarien in der realen Welt, die Zufälligkeit beinhalten.
Eine konzeptionelle Erklärung eines Zufallsspaziergangs. Bild mit freundlicher Genehmigung von napkin.ai.
Die Idee der Zufallsspaziergänge geht auf frühe Wahrscheinlichkeitsstudien zurück. Eines der frühesten Beispiele, oft als der Betrunkene-Spaziergänger-Weg bezeichnet, veranschaulicht, wie eine Person, die zufällig Schritte macht, eher unregelmäßig umherirrt, anstatt vorhersehbar auf ein Ziel zuzusteuern. Diese Zufälligkeit, kombiniert mit der Annahme, dass jeder Schritt unabhängig von den vorherigen ist, legte den Grundstein für moderne Zufallsspaziergangsmodelle.
Das Verständnis der Mathematik von Zufallsspaziergängen
Um Zufallsspaziergänge zu verstehen, beginnen wir mit einem einfachen Fall: einem eindimensionalen (1D) Zufallsspaziergang.Stellen Sie sich ein Teilchen auf einer Zahlengeraden vor. Es kann sich bei jedem Schritt entweder um +1 oder -1 entlang der Zahlengeraden bewegen. Jeder Schritt wird durch eine gleiche Wahrscheinlichkeit bestimmt, nach rechts oder links zu treten. Im Laufe der Zeit bildet die Position des Teilchens eine Wahrscheinlichkeitsverteilung, die sich ausbreitet und die Wahrscheinlichkeit widerspiegelt, es an verschiedenen Orten zu finden.
Dieses Prinzip kann auf zwei oder drei Dimensionen erweitert werden. Bei einem zweidimensionalen (2D) Zufallsspaziergang bewegt sich das Teilchen auf einer Ebene und kann mit gleicher Wahrscheinlichkeit in eine der vier Himmelsrichtungen (oben, unten, links, rechts) treten. Ebenso bewegt sich das Teilchen bei einem dreidimensionalen (3D) Zufallsspaziergang im Raum und kann mit gleicher Wahrscheinlichkeit in eine der sechs möglichen Richtungen (oben, unten, links, rechts, vorwärts, rückwärts) treten. Diese Zufallsspaziergänge in höheren Dimensionen erfassen noch komplexere und realistischere Szenarien.
Ein charakteristisches Merkmal von Zufallsspaziergängen ist ihre stochastische Natur, was bedeutet, dass jeder Schritt nur von der aktuellen Position abhängt und nicht von den vorherigen Schritten. Dies macht sie zu einer Art von Markow-Prozess – einem mathematischen Konzept, bei dem der zukünftige Zustand ausschließlich vom gegenwärtigen Zustand abhängt, nicht von der Abfolge der Ereignisse, die ihm vorausgingen. Diese „gedächtnislose“ Bewegung, kombiniert mit Wahrscheinlichkeitsverteilungen, die potenzielle Positionen beschreiben, bietet eine solide mathematische Grundlage für das Verständnis von Zufallsspaziergängen.
Wir können einen Zufallsspaziergang mithilfe statistischer Eigenschaften analysieren, um sein Verhalten im Laufe der Zeit zu verstehen. Dies umfasst die Untersuchung von Aspekten wie der erwarteten Entfernung vom Ausgangspunkt, der Wahrscheinlichkeitsverteilung möglicher Positionen und der Wahrscheinlichkeit, zum Ursprung zurückzukehren. Diese Analysen helfen uns, Zufälligkeit und Vorhersagbarkeit zu quantifizieren, Einblicke in Muster zu gewinnen und Vorhersagen zu treffen.
Schlüssel Eigenschaften von Zufallsspaziergängen
Zufallsspaziergänge haben mehrere wichtige Eigenschaften, die uns helfen, ihr Verhalten und ihre Anwendungen zu verstehen. Hier sind einige Schlüsselaspekte, die zu berücksichtigen sind:
Erwartungswert und Varianz
In einem eindimensionalen Zufallsspaziergang können wir die erwartete Entfernung (oder den mittleren Standort) vom Ausgangspunkt im Laufe der Zeit berechnen. Wenn jeder Schritt die gleiche Wahrscheinlichkeit hat, sich nach links oder rechts zu bewegen, bleibt die erwartete Position nach vielen Schritten null, was impliziert, dass der Wanderer im Durchschnitt in der Nähe des Ausgangspunkts bleibt.
Die Varianz der Position, die die Streuung oder Verteilung möglicher Positionen misst, nimmt mit jedem Schritt zu. Speziell bei einem symmetrischen Zufallsspaziergang wächst die Varianz linear mit der Anzahl der Schritte, was sie zu einem nützlichen Indikator für die typische Entfernung vom Ursprung im Laufe der Zeit macht.
Autokorrelation
Während einfache Zufallsspaziergänge keine Korrelation zwischen den Schritten aufweisen (jeder Schritt ist unabhängig vom letzten), führen bestimmte Arten von Zufallsspaziergängen Autokorrelation ein, bei der vergangene Schritte zukünftige beeinflussen können. Zum Beispiel können bei einem geneigten Zufallsspaziergang Schritte eine leichte Tendenz in eine Richtung haben, wodurch Positionen vorhersehbarer werden.
Autokorrelation in einem Zufallsspaziergang beeinflusst, wie wir den Fortschritt des Spaziergangs modellieren und vorhersagen. Dies ist insbesondere in Anwendungen relevant, in denen vergangenes Verhalten zukünftige Schritte beeinflusst, wie bei bestimmten Finanzmodellen.
Zentraler Grenzwertsatz
Das Zentrale Grenzwertsatz (CLT) besagt, dass die Summe einer großen Anzahl unabhängiger Zufallsvariablen dazu neigt, einer normalen (oder Gauß’schen) Verteilung zu folgen, unabhhängig von der ursprünglichen Verteilung. Im Kontext von Zufallsspaziergängen bedeutet dies, dass mit zunehmender Anzahl von Schritten die Verteilung der Positionen einer Normalverteilung ähnelt. Dies ist eine nützliche Eigenschaft, da es uns ermöglicht, die Wahrscheinlichkeit zu approximieren, den Wanderer in bestimmten Entfernungen vom Ausgangspunkt zu finden.
Gesetz der großen Zahlen
Das Gesetz der großen Zahlen (LLN) erklärt, dass mit zunehmender Anzahl von Versuchen oder Schritten der Durchschnitt der Ergebnisse gegen den wahren Durchschnitt konvergiert. Für Zufallsspaziergänge bedeutet dies, dass während die durchschnittliche Position null bleibt, die Varianz und der Bereich möglicher Positionen mit jedem weiteren Schritt vorhersehbar wachsen. Dieses Prinzip hilft, die Kluft zwischen reiner Zufälligkeit und vorhersagbaren statistischen Mustern in großen Stichproben zu überbrücken.
Arten von Zufallsspaziergängen
Zufällige Spaziergänge variieren stark je nach den Regeln, die jeden Schritt regeln. Diese Typen beeinflussen das Verhalten des Spaziergangs. Einige sind für einfache oder strukturierte Umgebungen ausgelegt, während andere für komplexere, realweltliche Phänomene ausgestattet sind. Lassen Sie uns einige der häufigsten Arten von zufälligen Spaziergängen erkunden.
1D, 2D und 3D zufällige Spaziergänge
Die Dimensionalität eines zufälligen Spaziergangs spielt eine grundlegende Rolle in seinem Verhalten. Bei einem 1D-Zufallsspaziergang ist jeder Schritt entweder ein Vorwärtsschritt oder ein Rückwärtsschritt entlang einer Linie. Dies macht den Spaziergang relativ einfach zu modellieren und vorherzusagen.
Wenn wir jedoch zu 2D (Ebene) und 3D (Raum) Spaziergängen übergehen, nehmen die möglichen Pfade signifikant zu und es treten neue Verhaltensweisen auf. Beispielsweise bleibt bei einem 2D-Zufallsspaziergang die Wahrscheinlichkeit, zum Ausgangspunkt zurückzukehren, hoch, während sie bei einem 3D-Zufallsspaziergang abnimmt.
Diese Änderung ist in Bereichen wie Physik und Chemie wichtig, wo sich Partikel je nach den dimensionsbezogenen Einschränkungen unterschiedlich diffundieren können.
Lattice Random Walk
Bei einem Lattice Random Walk ist die Bewegung auf diskrete Punkte eines Gitters oder einer Matrix beschränkt. Diese Art des Gehens wird in der Physik und Netzwerktheorie häufig verwendet, wo Knotenpunkte in einem Gitter angeordnet sind und Bewegungen nur zu benachbarten Knotenpunkten erfolgen können.
Ein häufiges Beispiel ist ein 2D-Gitter, bei dem jeder Schritt eine Bewegung zu benachbarten Punkten auf einem kartesischen Gitter ermöglicht. Diese Einschränkung vereinfacht die Modellierung, indem Bewegungspfade begrenzt werden, was nützlich ist, wenn komplexe Netzwerke oder molekulare Strukturen simuliert werden.
Gaussian Random Walk
In einem Gaußschen Zufallsspaziergang wird die Größe jedes Schritts durch eine Gaußsche (oder normale) Verteilung bestimmt. Anstatt sich um eine feste Entfernung zu bewegen, variiert die Schrittgröße gemäß einer Glockenkurvenverteilung, wobei die meisten Schritte klein sind und gelegentlich größere Sprünge auftreten. Diese Art von Spaziergang wird häufig in der Finanzmodellierung verwendet, um die Variabilität bei Preisänderungen von Vermögenswerten zu berücksichtigen.
Heterogene und voreingenommene Zufallsspaziergänge
Heterogene und voreingenommene Zufallsspaziergänge ermöglichen Variationen in Schrittrichtung und -größe basierend auf bestimmten Wahrscheinlichkeiten. Diese Flexibilität macht sie anpassungsfähiger an reale Szenarien.
In einem heterogenen Zufallsspaziergang kann die Wahrscheinlichkeit, sich in eine bestimmte Richtung zu bewegen, je nach Standort oder externen Bedingungen variieren. Zum Beispiel bevorzugen Tiere bei der Nahrungssuche möglicherweise Gebiete mit bekannten Ressourcen, was einen voreingenommenen Zufallsspaziergang erzeugt. Diese Spaziergänge sind nützlich für die Untersuchung von Verhaltensweisen, die von Kontextfaktoren abhängen.
Zufallsspaziergang mit Drift
In einem zufälligen Spaziergang mit Drift gibt es eine beständige Tendenz, sich in eine Richtung zu bewegen. Zum Beispiel können Aktienkurse trotz täglicher Schwankungen im Laufe der Zeit insgesamt einen Aufwärtstrend aufweisen. Der Drift in diesen Spaziergängen repräsentiert eine externe Kraft oder einen Trend, die den Pfad beeinflussen. Dieser Typ wird oft in der Finanzwelt gesehen, wo Modelle einen Driftterm enthalten, um Wachstum oder Rückgang darzustellen und einen realistischeren Ansatz zur Vorhersage von Vermögenspreisen und Markttrends zu bieten.
Jede dieser Arten von zufälligen Spaziergängen dient einem einzigartigen Zweck und bietet verschiedene Möglichkeiten, zufälliges, aber strukturiertes Verhalten zu modellieren. Die dimensionsbezogenen Einschränkungen, die Verteilung der Schritte und das Vorhandensein von Drift oder Voreingenommenheit machen zufällige Spaziergänge äußerst vielseitig für die Datenmodellierung und Simulation in verschiedenen Bereichen.
Reale Anwendungen von zufälligen Spaziergängen
Zufällige Spaziergänge sind mehr als nur theoretische Konstrukte; sie spielen eine wesentliche Rolle in vielen praktischen Anwendungen in verschiedenen Disziplinen. Lassen Sie uns erkunden, wie zufällige Spaziergänge das reale Problem- und Lösungsfindung in verschiedenen Sektoren beeinflussen.
Anwendungen in den Datenwissenschaften und im maschinellen Lernen
Informatik
Zufällige Spaziergänge bilden die Grundlage für mehrere Informatik-Algorithmen, wie zufällige Stichproben, Webgraph-Durchquerung und Bildsegmentierung. Zum Beispiel verwendete Googles PageRank-Algorithmus zufällige Spaziergänge, um Webseiten basierend auf ihrer Relevanz zu bewerten, indem simuliert wurde, wie ein Benutzer zufällig zwischen Links im Internet navigieren könnte.
Merkmalsextraktion
Im maschinellen Lernen können zufällige Spaziergänge dazu beitragen, Merkmale zu extrahieren, indem Beziehungen zwischen Datenpunkten hervorgehoben werden. Zum Beispiel können zufällige Spaziergänge in der Netzwerkanalyse Cluster oder Gemeinschaften aufzeigen und bei Aufgaben wie Empfehlungssystemen und sozialer Netzwerkanalyse unterstützen.
Anomalieerkennung
Zufällige Spaziergänge können auch verwendet werden, um Anomalien in Datensätzen zu erkennen. Wenn Datenpunkte signifikant von einem typischen Pfad in einem zufälligen Spaziergangsmodell abweichen, könnten diese Punkte auf ungewöhnliche Ereignisse oder Fehler in den Daten hinweisen. Die Anomalieerkennung ist insbesondere in Bereichen wie Cybersicherheit und Betrugsbekämpfung wertvoll.
Simulation stochastischer Prozesse
Zufallswanderungen simulieren stochastische oder zufällig bestimmte Prozesse und ermöglichen es Datenwissenschaftlern, unberechenbare Phänomene der realen Welt zu modellieren. Durch die Simulation von Zufallswanderungen können wir Einblicke in Systeme gewinnen, in denen eine präzise Vorhersage herausfordernd ist, wie zum Beispiel bei Wettermustern oder Kundenverhalten.
Zeitreihenprognosen
Bei der Zeitreihenanalyse bilden Zufallswanderungen die Grundlage für bestimmte Prognosemodelle, einschließlich der Zufallswanderungshypothese in der Finanzwelt. Diese Modelle nehmen an, dass zukünftige Werte in einer Zeitreihe ausschließlich vom letzten Wert abhängen, ohne Korrelation zu vergangenen Trends. Weitere Informationen zur Zeitreihenprognose finden Sie in ARIMA für die Zeitreihenprognose: Ein umfassender Leitfaden. Nehmen Sie auch an unserem Kurs Prognosen in R mit Professor Hyndman teil, der Zufallswanderungsmodelle mit naiven und saisonalen naiven Prognosemethoden verbindet.
Anwendungen in anderen Bereichen
Finanzen
Eine der bemerkenswertesten Anwendungen von Zufallsspaziergängen liegt im Finanzmodellierungsbereich, insbesondere zur Vorhersage von Aktienkursen. Die Effizienzmarkthypothese legt nahe, dass Aktienkursbewegungen im Wesentlichen zufällig sind, da neue Informationen sofort absorbiert werden und zukünftige Preise unberechenbar machen. Zufallsspaziergänge können verwendet werden, um Aktienkursänderungen im Laufe der Zeit zu modellieren und zu veranschaulichen, wie Preise ohne einen vorhersehbaren Pfad schwanken.
Mathematik
In der reinen Mathematik liefern Zufallsspaziergänge Lösungen für komplexe Probleme. Sie sind beispielsweise nützlich zur Lösung der Laplace-Gleichung, zur Analyse von Netzwerken und zur Erforschung der Kombinatorik.
Physik und Chemie
In den Naturwissenschaften sind Zufallsspaziergänge entscheidend für die Modellierung von Diffusionsprozessen, wie beispielsweise die Art und Weise, wie Moleküle sich durch ein Medium ausbreiten. Die Brownsche Bewegung, bei der Teilchen in einer Flüssigkeit aufgrund von Kollisionen mit umgebenden Molekülen unberechenbar bewegt werden, ist ein klassisches Beispiel, das genau mithilfe von Zufallsspaziergängen simuliert werden kann. So habe ich tatsächlich zum ersten Mal von Zufallsspaziergängen erfahren.
Biologie
Zufällige Spaziergänge sind in der Ökologie wertvoll, um Bewegungsmuster von Tieren zu untersuchen. Tiere, die nach Ressourcen suchen, scheinen sich manchmal zufällig zu bewegen, manchmal aber auch in Regionen mit bekannten Ressourcen zu tendieren. Andere biologische Konzepte, wie die Ausbreitung von Populationen oder Genen, können oft mit den Prinzipien zufälliger Spaziergänge modelliert werden, was es einfacher macht, Veränderungen in Ökosystemen zu verstehen und vorherzusagen.
Spezialfälle und Varianten von Zufallsspaziergängen
Neben dem klassischen Zufallsspaziergang gibt es mehrere fortgeschrittene Varianten, die das Konzept für spezialisierte Anwendungen erweitern.
Selbstvermeidende Spaziergänge
Ein selbstvermeidender Spaziergang ist ein Zufallsspaziergang, bei dem der Pfad keine Position wiederholt, die er bereits passiert hat. Diese Variante ist besonders nützlich in Bereichen wie der Polymerchemie, wo sie modellieren kann, wie Polymerketten entstehen, ohne sich zu kreuzen. Da jeder Schritt zuvor besuchte Punkte vermeidet, sind selbstvermeidende Spaziergänge stärker eingeschränkt als traditionelle Zufallsspaziergänge. Das bedeutet, dass sie rechnerisch anspruchsvoll sind, aber nützlich, um nicht überlappende Wege in begrenzten Räumen zu verstehen.
Verzweigende
Bei verzweigenden Zufallswanderungen kann der Pfad in mehrere Zweige aufgeteilt werden, wobei jeder Zweig einer zufälligen Wanderung folgt. Diese Art von Wanderung ist entscheidend für die Modellierung von Verzweigungsprozessen wie Zellteilung oder der Verbreitung von Informationen durch Netzwerke. Jeder „Zweig“ repräsentiert einen unabhängigen zufälligen Pfad, der von einer gemeinsamen Quelle ausgeht.
Korrelierte Wanderungen
Korrelierte Wanderungen gehen einen Schritt weiter, bei dem die Richtung jedes Schrittes teilweise vom vorherigen Schritt beeinflusst wird. Diese Variante ist nützlich für die Modellierung von Trägheit in Systemen, in denen Veränderungen allmählich statt zufällig eintreten. Korrelierte Wanderungen werden häufig in der Finanzwelt angewendet, um Preisentwicklungen zu simulieren, oder in der Bewegungsforschung, um zu verstehen, wie Tiere ihre Umgebung mit einer gewissen Erinnerung an ihre frühere Richtung navigieren.
Schleifenbereinigte Wanderungen
Bei einer schleifenbereinigten Wanderung werden Schleifen oder Pfade, die sich kreuzen, während ihrer Bildung entfernt. Jedes Mal, wenn ein Schritt eine Position erneut besucht, wird die dazwischenliegende Schleife gelöscht und hinterlässt einen schlanken, nicht wiederholenden Pfad. Schleifenbereinigte Wanderungen werden häufig in der Netzwerkanalyse und bei der Erzeugung von Labyrinthen eingesetzt, da sie Pfade erzeugen, die Redundanzen vermeiden.
Implementieren von Zufallswanderungen in Python
Lassen Sie uns versuchen, eine Zufallswanderung in Python zu implementieren. Um zu beginnen, stellen Sie sicher, dass Sie Python installiert haben (wir werden Python 3.10 verwenden) und die erforderlichen Bibliotheken verfügbar sind. Sie können fehlende Bibliotheken mit pip installieren. Hier ist, was wir verwenden werden:
import numpy as np # für numerische Operationen und Generierung von zufälligen Schritten import matplotlib.pyplot as plt # für das Plotten und Visualisieren der Zufallswanderungen
1D Zufallswanderung
Wir beginnen mit einer einfachen eindimensionalen Zufallswanderung, bei der jeder Schritt zufällig entweder +1 oder -1 ist.
# Parameter n_steps = 100 # Anzahl der Schritte # Generiere zufällige Schritte: +1 oder -1 steps = np.random.choice([-1, 1], size=n_steps) # Berechne Positionen positions = np.cumsum(steps) # Plotte die Zufallswanderung plt.figure(figsize=(10, 6)) plt.plot(positions, marker='o', linestyle='-', markersize=4) plt.title("1D Random Walk") plt.xlabel("Step") plt.ylabel("Position") plt.grid(True) plt.show()
Dies erzeugt einen einfachen Zufallsspaziergang und visualisiert die Entwicklung im Laufe der Zeit. Hier ist die Ausgabe, wenn ich diesen Code ausführe:
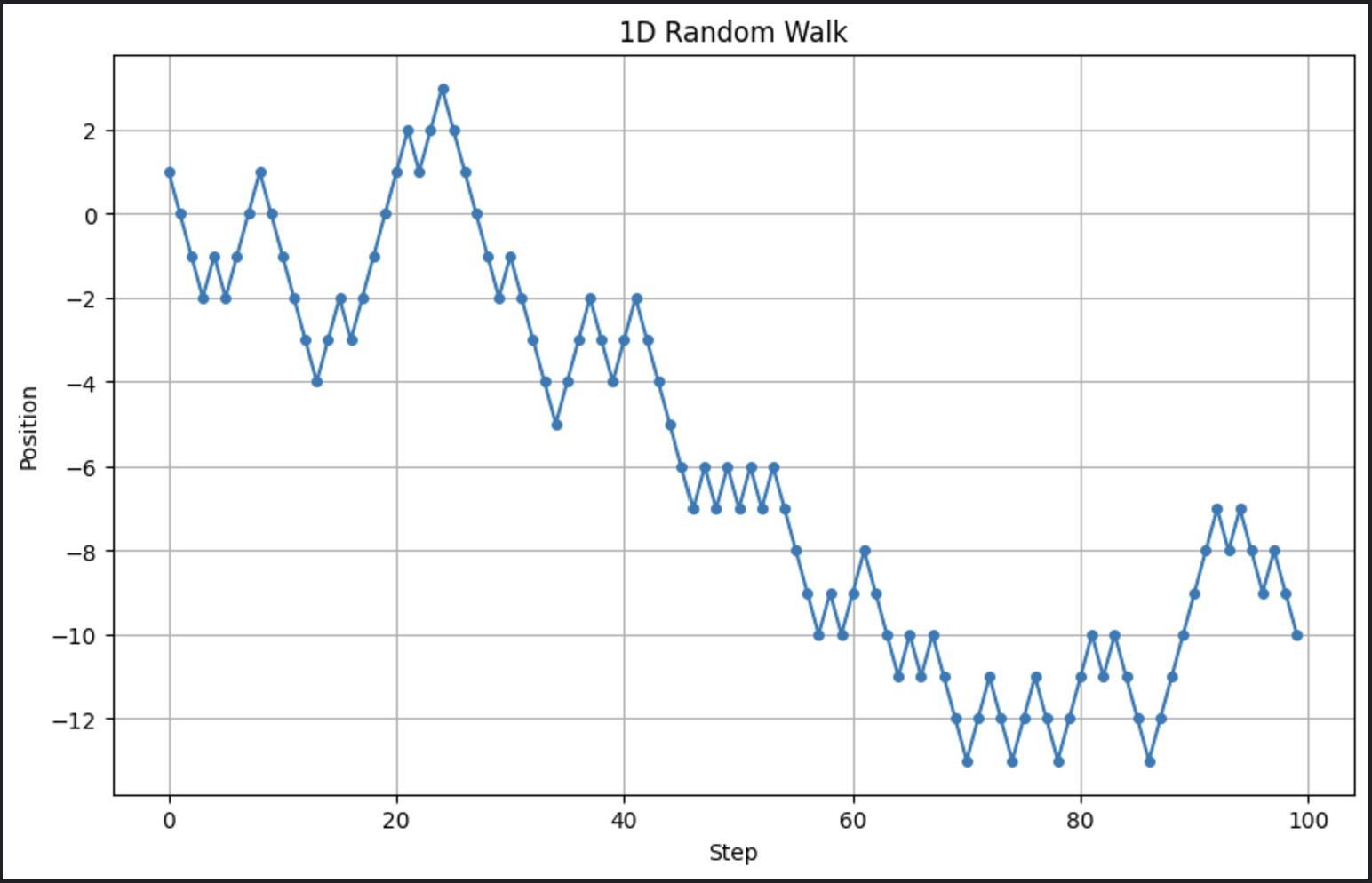
Vergiss nicht, wir führen ein stochastisches Modell aus. Das bedeutet, dass jedes Mal, wenn wir es ausführen, die Ausgabe ein wenig anders aussieht.
2D Zufallsspaziergang
Jetzt erweitern wir den Zufallsspaziergang auf zwei Dimensionen. Bei jedem Schritt wird die Richtung zufällig gewählt.
# Parameter n_steps = 500 # Generiere zufällige Schritte in x- und y-Richtungen x_steps = np.random.choice([-1, 1], size=n_steps) y_steps = np.random.choice([-1, 1], size=n_steps) # Berechne Positionen x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Plot des 2D Zufallsspaziergangs plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Roter Punkt für Start plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Schwarzer Punkt für Ende plt.title("2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Stellt eine gleichmäßige Skalierung für beide Achsen sicher plt.legend() plt.show()
Dieser Code erstellt einen visuell ansprechenden Pfad in zwei Dimensionen.
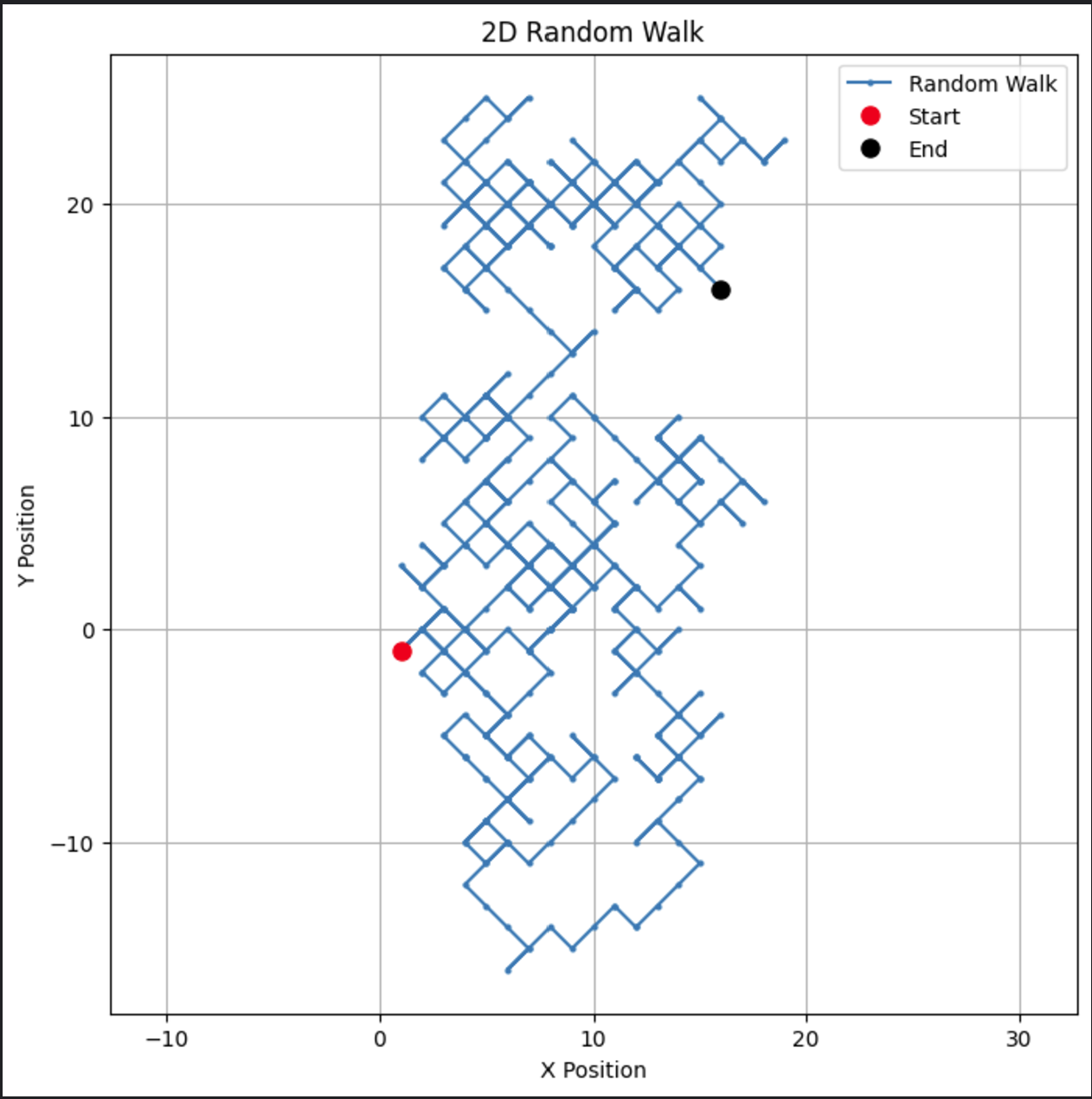
Dieser Typ eines zweidimensionalen Zufallsspaziergangs könnte modifiziert werden, um Anwendungen wie Teilchenbewegungen oder räumliche Modellierung zu ermöglichen.
Verzerrter Zufallsspaziergang
Zuletzt werfen wir einen Blick auf ein etwas komplexeres Beispiel: einen verzerrten Zufallsspaziergang. Um eine Verzerrung einzuführen, können wir die Wahrscheinlichkeiten für jede Schrittrichtung anpassen. Zum Beispiel könnten wir aufwärts gerichtete Schritte wahrscheinlicher machen.
# Parameter n_steps = 100 bias = 0.7 # Wahrscheinlichkeit für einen Schritt von +1 # Erzeugen von verzerrten zufälligen Schritten in x- und y-Richtungen x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) # Berechnen der Positionen x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Plotten des verzerrten 2D-Zufallsspaziergangs plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Roter Punkt für den Start plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Schwarzer Punkt für das Ende plt.title("Biased 2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Sorgt für eine gleichmäßige Skalierung beider Achsen plt.legend() plt.show()
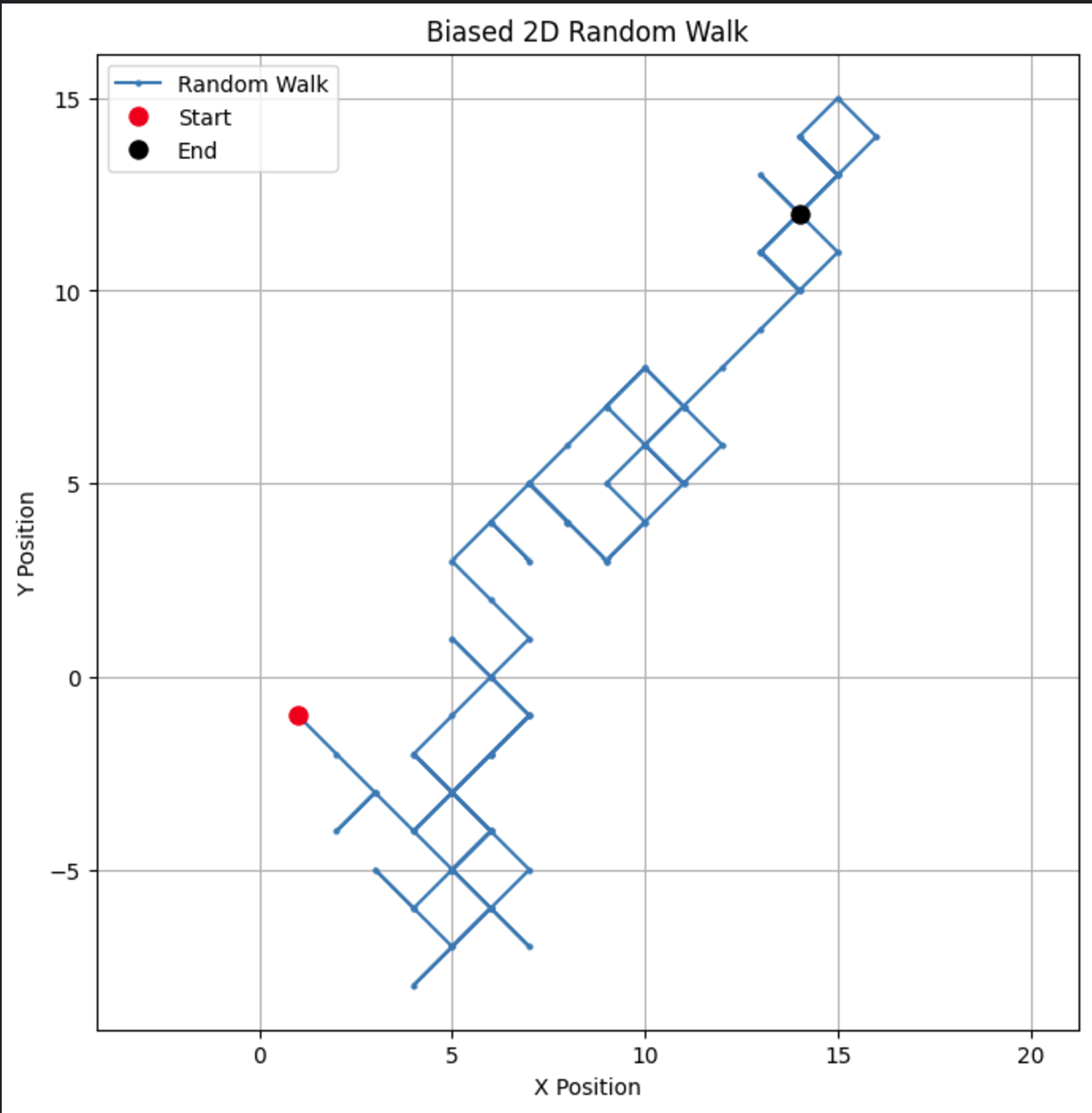
Durch Ändern des Bias können Sie beobachten, wie der Weg dazu neigt, eine bestimmte Richtung zu bevorzugen, wodurch reale Szenarien wie Drift bei Aktienkursen oder Tierwanderungsmuster simuliert werden.
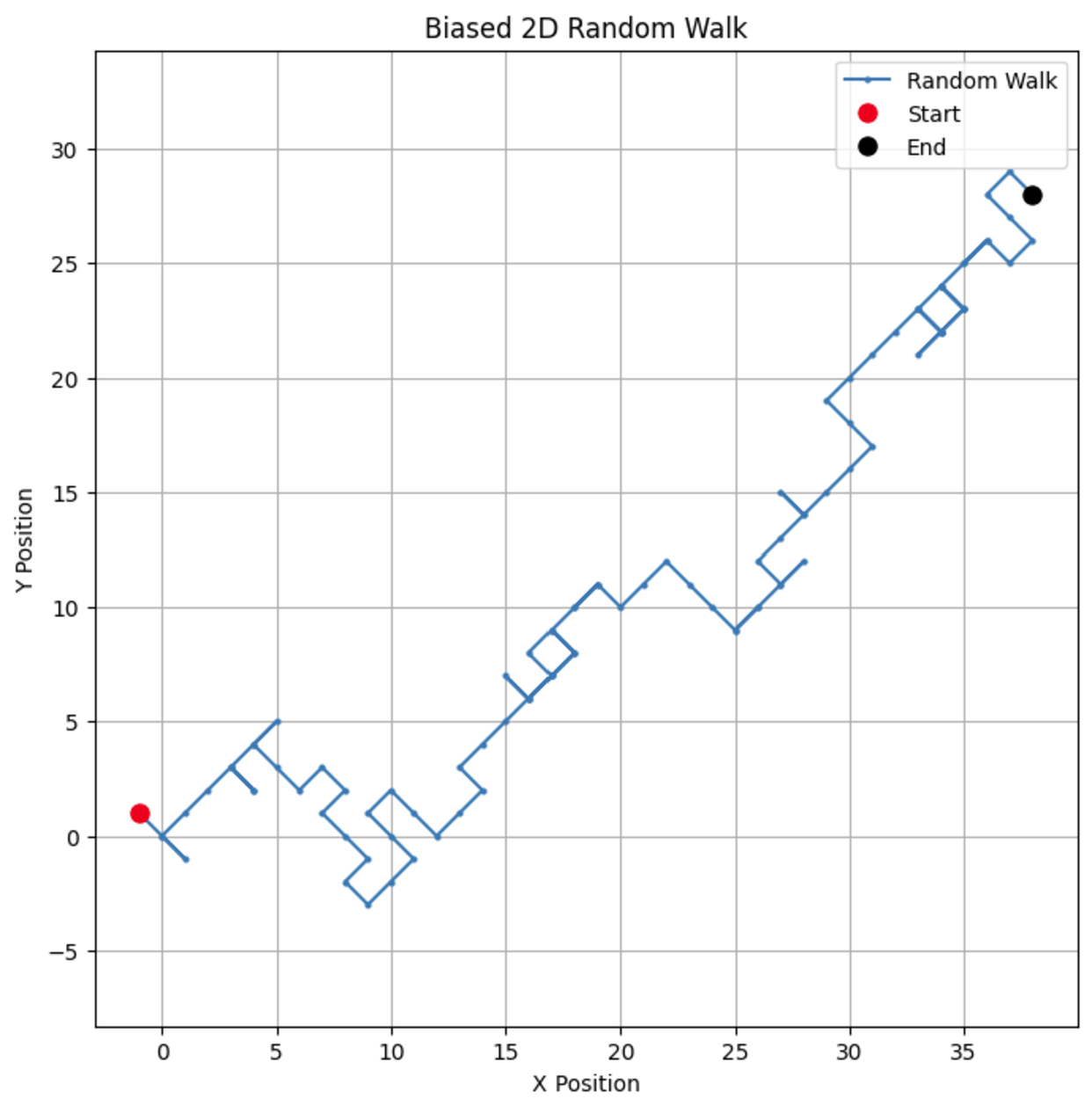
Wenn wir den Bias-Parameter auf 0,55 ändern, sehen wir einen dramatischen Unterschied im Verhalten des Modells. Obwohl es immer noch eine Tendenz zum Aufwärtsgehen hat, ist der Bias nicht so stark, was zu mehr Schleifen und Umwegen führt.
Schlussfolgerung
Zufallswanderungen sind ein wertvolles Modellierungswerkzeug für Datenwissenschaftler und in Bereichen von Physik bis Finanzen und darüber hinaus anwendbar. Ihre Fähigkeit, komplexe stochastische Prozesse zu modellieren, macht sie in vielen realen Szenarien unverzichtbar.
Hungrig nach mehr? Schau dir DataCamps Suite von Wahrscheinlichkeits- und Statistik-Kursen an. Du findest alle Arten von großartigen Kursen sowohl in Python als auch in R. Wenn du an fortgeschrittenerem Inhalt interessiert bist, schau dir DataCamps Kurs zu Statistischer Simulation in Python und das Tutorial zur Einführung in das maschinelle Lernen an. Oder wenn du bereit bist, dein Wissen zu testen, versuche dich an einigen dieser Wahrscheinlichkeitsrätsel.













