На моем первом курсе статистики на основе кодирования в колледже мой преподаватель поставил вопрос: как мы можем моделировать броуновское движение одной пыльцы в чашке с водой? После нескольких ошибочных попыток я и мои однокурсники наконец-то наткнулись на правильный ответ: случайное блуждание. Позже я узнал, что эта простая модель используется для моделирования всевозможных вещей, начиная от движения животных до колебаний цен на фондовом рынке.
В этой статье мы рассмотрим математические основы случайных блужданий, изучим различные типы и обсудим их применение. Часть того, что делает случайное блуждание интересным, заключается в том, что оно используется во многих различных областях. Кроме моего примера, в физике оно помогает описать движение частиц; в финансах моделирует колебания цен на акции; а в биологии объясняет закономерности движения животных. Случайные блуждания отражают случайность реального мира, что является ключом к моделированию стохастических процессов.
Для тех, кто хочет построить прочный фундамент в статистике, лежащей в основе теории случайного блуждания, мы рекомендуем начать с курса Введение в статистику в R или курса Введение в статистику в Python.
Что такое случайные блуждания?
В теории вероятностей случайное блуждание – это модель, описывающая последовательность случайных шагов, образующих путь. Или иначе, можно сказать, что случайное блуждание – это математическая модель, описывающая путь, образованный последовательностью шагов, каждый из которых определяется независимо и с определенной вероятностью. Эта стохастичность делает случайные блуждания непредсказуемыми.
Представьте себе человека, делающего шаг в случайном направлении на каждом шаге. Со временем его путь образует непредсказуемый, извилистый след. Несмотря на свою простоту, этот концепт обладает удивительной глубиной и универсальностью, моделируя различные сценарии реального мира, связанные с случайностью.
Концептуальное объяснение случайного блуждания. Изображение предоставлено napkin.ai.
Идея случайных блужданий уходит корнями в ранние исследования вероятности. Один из ранних примеров, часто называемый блужданием пьяницы, иллюстрирует, как человек, делающий случайные шаги, будет бродить хаотично, а не двигаться предсказуемо к цели. Эта случайность, в сочетании с предположением о том, что каждый шаг независим от предыдущих, заложила основу для современных моделей случайных блужданий.
Понимание математики случайных блужданий
Для понимания случайных блужданий начнем с простого случая: одномерного (1D) случайного блуждания.Представьте частицу на числовой прямой. Она может перемещаться либо +1, либо -1 вдоль числовой прямой с каждым шагом. Каждое движение определяется равной вероятностью шагнуть вправо или влево. Со временем позиция частицы формирует распределение вероятности, которое распространяется, представляя вероятность найти ее в различных местах.
Этот принцип можно расширить на два или три измерения. В двумерном (2D) случайном блуждании частица перемещается по плоскости и может делать шаг в любом из четырех кардинальных направлений (вверх, вниз, влево, вправо) с равной вероятностью. Аналогично, в трехмерном (3D) случайном блуждании частица перемещается в пространстве и может делать шаг в любом из шести возможных направлений (вверх, вниз, влево, вправо, вперед, назад) с равной вероятностью. Эти случайные блуждания более высокой размерности описывают еще более сложные и реалистичные сценарии.
Особенностью случайных блужданий является их стохастический характер, что означает, что каждый шаг зависит только от текущего положения, а не от предыдущих шагов. Это делает их разновидностью процесса Маркова — математического концепта, в котором будущее состояние зависит исключительно от текущего состояния, а не от последовательности событий, предшествовавших ему. Это “безпамятное” движение, совместно с вероятностными распределениями, описывающими потенциальные положения, обеспечивает прочную математическую основу для понимания случайных блужданий.
Мы можем проанализировать случайное блуждание, используя статистические свойства, чтобы понять его поведение со временем. Это включает изучение аспектов, таких как ожидаемое расстояние от начальной точки, вероятностное распределение возможных позиций и вероятность возвращения к началу. Эти анализы помогают нам количественно оценить случайность и предсказуемость, дать представление о закономерностях и сделать прогнозы.
Ключевые свойства случайных блужданий
Случайные блуждания имеют несколько важных свойств, которые помогают нам понять их поведение и применение. Вот несколько ключевых аспектов, которые стоит рассмотреть:
Ожидание и дисперсия
В одномерном случайном блуждании мы можем рассчитать ожидаемое расстояние (или среднюю позицию) от начальной точки со временем. Если каждый шаг имеет равную вероятность движения влево или вправо, ожидаемая позиция после многих шагов остается нулевой, что подразумевает, что в среднем человек остается около начальной точки.
Однако дисперсия позиции, которая измеряет разброс возможных позиций, увеличивается с каждым шагом. Конкретно, в симметричном случайном блуждании, дисперсия растет линейно с числом шагов, делая ее полезным индикатором типичного расстояния от начала координат со временем.
Автокорреляция
Хотя простые случайные блуждания не имеют корреляции между шагами (каждый шаг независим от предыдущего), некоторые типы случайных блужданий вводят автокорреляцию, где прошлые шаги могут влиять на будущие. Например, в смещенном случайном блуждании шаги могут иметь небольшую тенденцию в одном направлении, что делает позиции более предсказуемыми.
Автокорреляция в случайном блуждании влияет на то, как мы моделируем и предсказываем прогресс блуждания. Это особенно актуально в приложениях, где прошлое поведение влияет на будущие шаги, таких как определенные финансовые модели.
Центральная предельная теорема
Центральная предельная теорема (ЦПТ) говорит нам, что сумма большого количества независимых случайных величин имеет тенденцию следовать нормальному (или гауссовскому) распределению, независимо от исходного распределения. В контексте случайных блужданий это означает, что с увеличением числа шагов распределение позиций начинает напоминать нормальное распределение. Это полезное свойство, потому что позволяет нам приблизительно оценить вероятность нахождения человека в определенном расстоянии от начальной точки.
Закон больших чисел
Закон больших чисел (ЗБЧ) объясняет, что с увеличением числа испытаний или шагов среднее значение результатов сходится к истинному среднему. Для случайных блужданий это означает, что в то время как средняя позиция остается нулевой, дисперсия и диапазон возможных позиций предсказуемо увеличиваются с каждым дополнительным шагом. Этот принцип помогает сократить разрыв между чистой случайностью и предсказуемыми статистическими закономерностями в больших выборках.
Типы случайных блужданий
Случайные блуждания сильно различаются в зависимости от правил, регулирующих каждый шаг. Эти типы влияют на поведение блуждания. Некоторые из них предназначены для простых или структурированных сред, в то время как другие предназначены для более сложных, реальных явлений. Давайте рассмотрим некоторые из наиболее распространенных типов случайных блужданий.
1D, 2D и 3D случайные блуждания
Размерность случайного блуждания играет фундаментальную роль в его поведении. В 1D случайном блуждании каждый шаг представляет собой либо движение вперед, либо движение назад по линии. Это делает моделирование и прогнозирование блуждания относительно простым.
Однако, когда мы переходим к 2D (плоскость) и 3D (пространство) блужданиям, возможные пути значительно увеличиваются, что приводит к появлению нового поведения. Например, в 2D случайном блуждании вероятность вернуться в исходную точку остается высокой, в то время как в 3D случайном блуждании эта вероятность уменьшается.
Это изменение важно в таких областях, как физика и химия, где частицы могут диффундировать по-разному в зависимости от размерных ограничений.
Случайное блуждание по решетке
В случайном блуждании по решетке движение ограничено дискретными точками на сетке или решетке. Этот тип блуждания часто используется в физике и теории сетей, где узлы расположены в сетке, и перемещение может происходить только к соседним узлам.
Одним из распространенных примеров является 2D-решетка, где каждый шаг позволяет перемещаться к смежным точкам на декартовой сетке. Это ограничение упрощает моделирование, ограничивая пути перемещения, что полезно при симуляции сложных сетей или молекулярных структур.
Гауссово случайное блуждание
В гауссовом случайном блуждании, размер каждого шага определяется гауссовым (или нормальным) распределением. Вместо движения на фиксированное расстояние размер шага варьируется в соответствии с распределением колокольчика, где большинство шагов маленькие, а иногда бывают и большие скачки. Этот тип блуждания часто используется в финансовом моделировании для учета изменчивости цен на активы.
Гетерогенные и смещенные случайные блуждания
Гетерогенные и смещенные случайные блуждания позволяют варьировать направление и размер шага на основе определенных вероятностей. Эта гибкость делает их более приспособленными к реальным сценариям.
В гетерогенном случайном блуждании вероятность движения в любом направлении может изменяться в зависимости от местоположения или внешних условий. Например, животные, ищущие пищу, могут предпочитать области с известными ресурсами, что создает смещенное случайное блуждание. Эти блуждания полезны для изучения поведения, зависящего от контекстуальных факторов.
Случайное блуждание с дрейфом
В случайном блуждании с дрейфом, существует постоянная тенденция двигаться в одном направлении. Например, цены на акции могут проявлять общий восходящий тренд со временем, несмотря на ежедневные колебания. Дрейф в этих блужданиях представляет собой внешнюю силу или тенденцию, влияющую на путь. Этот тип часто встречается в финансах, где модели включают дрейфовый член для представления роста или упадка, обеспечивая более реалистичный подход к прогнозированию цен на активы и тенденций на рынке.
Каждый из этих типов случайного блуждания служит уникальной цели, предлагая различные способы моделирования случайного, но структурированного поведения. Размерные ограничения, распределение шагов и наличие дрейфа или смещения делают случайные блуждания чрезвычайно универсальными для моделирования данных и симуляции в различных областях.
Прикладные задачи случайных блужданий
Случайные блуждания – это не просто теоретические конструкции; они играют важную роль во многих практических приложениях в различных областях. Давайте исследуем, как случайные блуждания информируют о решении реальных проблем в различных секторах.
Применения в области науки о данных и машинного обучения
Информатика
Случайные блуждания лежат в основе нескольких алгоритмов в области компьютерных наук, таких как случайная выборка, обход веб-графа и сегментация изображений. Например, алгоритм PageRank Google использует случайные блуждания для ранжирования веб-страниц на основе их релевантности, имитируя, как пользователь может случайно перемещаться между ссылками в интернете.
Извлечение признаков
В машинном обучении случайные блуждания могут помочь извлечь признаки, выделяя отношения между точками данных. Например, в анализе сетей случайные блуждания могут выявить кластеры или сообщества, помогая в задачах, таких как рекомендательные системы и анализ социальных сетей.
Выявление аномалий
Случайные блуждания также могут использоваться для обнаружения аномалий в наборах данных. Например, если точки данных значительно отклоняются от типичного пути в модели случайного блуждания, эти точки могут указывать на необычные события или ошибки в данных. Выявление аномалий особенно ценно в областях, таких как кибербезопасность и обнаружение мошенничества.
Моделирование стохастических процессов
Случайные блуждания моделируют стохастические, или случайно обусловленные, процессы, позволяя специалистам по данным моделировать непредсказуемые явления реального мира. Симулируя случайные блуждания, мы можем получить понимание систем, где точное предсказание сложно, таких как погодные условия или поведение клиентов.
Прогнозирование временных рядов
В анализе временных рядов случайные блуждания являются основой для определенных моделей прогнозирования, включая гипотезу о случайном блуждании в финансах. Эти модели предполагают, что будущие значения во временном ряду зависят исключительно от последнего значения, не имея корреляции с прошлыми тенденциями.Для получения дополнительной информации о прогнозировании временных рядов, ознакомьтесь с ARIMA для прогнозирования временных рядов: Полное руководство. Также пройдите наш курс Прогнозирование в R с профессором Хиндманом, который связывает модели случайного блуждания с наивными и сезонными наивными методами прогнозирования.
Применение в других областях
Финансы
Одно из наиболее заметных применений случайных блужданий – в финансовом моделировании, особенно для прогнозирования цен на акции. Гипотеза об эффективности рынка предполагает, что движения цен на акции в основном случайны, поскольку новая информация моментально усваивается, что делает будущие цены непредсказуемыми. Случайные блуждания могут использоваться для моделирования изменений цен на акции со временем, иллюстрируя, как цены колеблются без предсказуемого пути.
Математика
В чистой математике случайные блуждания предоставляют решения для сложных проблем. Например, они полезны для решения уравнения Лапласа, анализа сетей и изучения комбинаторики.
Физика и химия
В естественных науках случайные блуждания имеют важное значение для моделирования процессов диффузии, таких как распространение молекул через среду. Броуновское движение, где частицы, подвешенные в жидкости, двигаются непредсказуемо из-за столкновений с окружающими молекулами, является классическим примером, который можно точно смоделировать с использованием случайных блужданий. Именно так я впервые узнал о случайных блужданиях.
Биология
Случайные блуждания ценны в экологии для изучения движения животных. Животные, ищущие пищу, могут казаться двигающимися в случайном порядке, иногда смещаясь в сторону областей с известными ресурсами. Другие биологические концепции, такие как распространение популяций или генов, часто могут быть смоделированы с принципами случайного блуждания, что упрощает понимание и прогнозирование изменений в экосистемах.
Специальные случаи и варианты случайных блужданий
Помимо классического случайного блуждания, существует несколько продвинутых вариантов, расширяющих концепцию для специализированных приложений.
Самоизбегающие блуждания
Самоизбегающее блуждание – это случайное блуждание, в котором путь не посещает ни одной позиции, которую он уже прошел. Этот вариант особенно полезен в областях, таких как полимерная химия, где он может моделировать, как цепи полимеров формируются, не пересекаясь. Поскольку каждый шаг избегает ранее посещенных точек, самоизбегающие блуждания более ограничены, чем традиционные случайные блуждания. Это означает, что они представляют вычислительные сложности, но полезны для понимания не пересекающихся путей в ограниченных пространствах.
Разветвляющийся
В ветвящихся случайных блужданиях путь может разделяться на несколько ветвей, при этом каждая ветвь следует случайному пути. Этот тип блуждания является важным при моделировании ветвящихся процессов, таких как деление клеток или распространение информации через сети. Каждая “ветвь” представляет собой независимый случайный путь, исходящий из общего источника.
Коррелированные блуждания
Коррелированные блуждания заходят еще дальше, где направление каждого шага частично зависит от предыдущего шага. Этот вариант полезен для моделирования инерции в системах, где изменения происходят постепенно, а не случайным образом. Коррелированные блуждания часто применяются в финансах для моделирования тенденций цен или в экологии движения для понимания того, как животные ориентируются в своем окружении с некоторой памятью о своем прошлом направлении.
Блуждания с удалением петель
Блуждание с удалением петель – это вариант, при котором петли или пути, пересекающие себя, удаляются по мере их образования. Каждый раз, когда шаг повторно посещает позицию, промежуточная петля удаляется, оставляя упрощенный, не повторяющийся путь. Блуждания с удалением петель часто применяются в анализе сетей и алгоритмах генерации лабиринтов, потому что они создают пути, избегающие избыточности.
Реализация случайных блужданий на Python
Давайте попробуем реализовать случайное блуждание на Python. Для начала убедитесь, что у вас установлен Python (мы будем использовать Python 3.10) и необходимые библиотеки доступны. Вы можете установить недостающие библиотеки с помощью pip. Вот что мы будем использовать:
import numpy as np # для числовых операций и генерации случайных шагов import matplotlib.pyplot as plt # для построения графиков и визуализации случайных блужданий
Одномерное случайное блуждание
Мы начнем с простого одномерного случайного блуждания, где каждый шаг равен либо +1, либо -1, выбирается случайно.
# Параметры n_steps = 100 # Количество шагов # Генерация случайных шагов: +1 или -1 steps = np.random.choice([-1, 1], size=n_steps) # Расчет позиций positions = np.cumsum(steps) # Построение случайного блуждания plt.figure(figsize=(10, 6)) plt.plot(positions, marker='o', linestyle='-', markersize=4) plt.title("1D Random Walk") plt.xlabel("Step") plt.ylabel("Position") plt.grid(True) plt.show()
Этот код генерирует простую случайную прогулку и визуализирует прогресс со временем. Вот вывод при запуске этого кода:
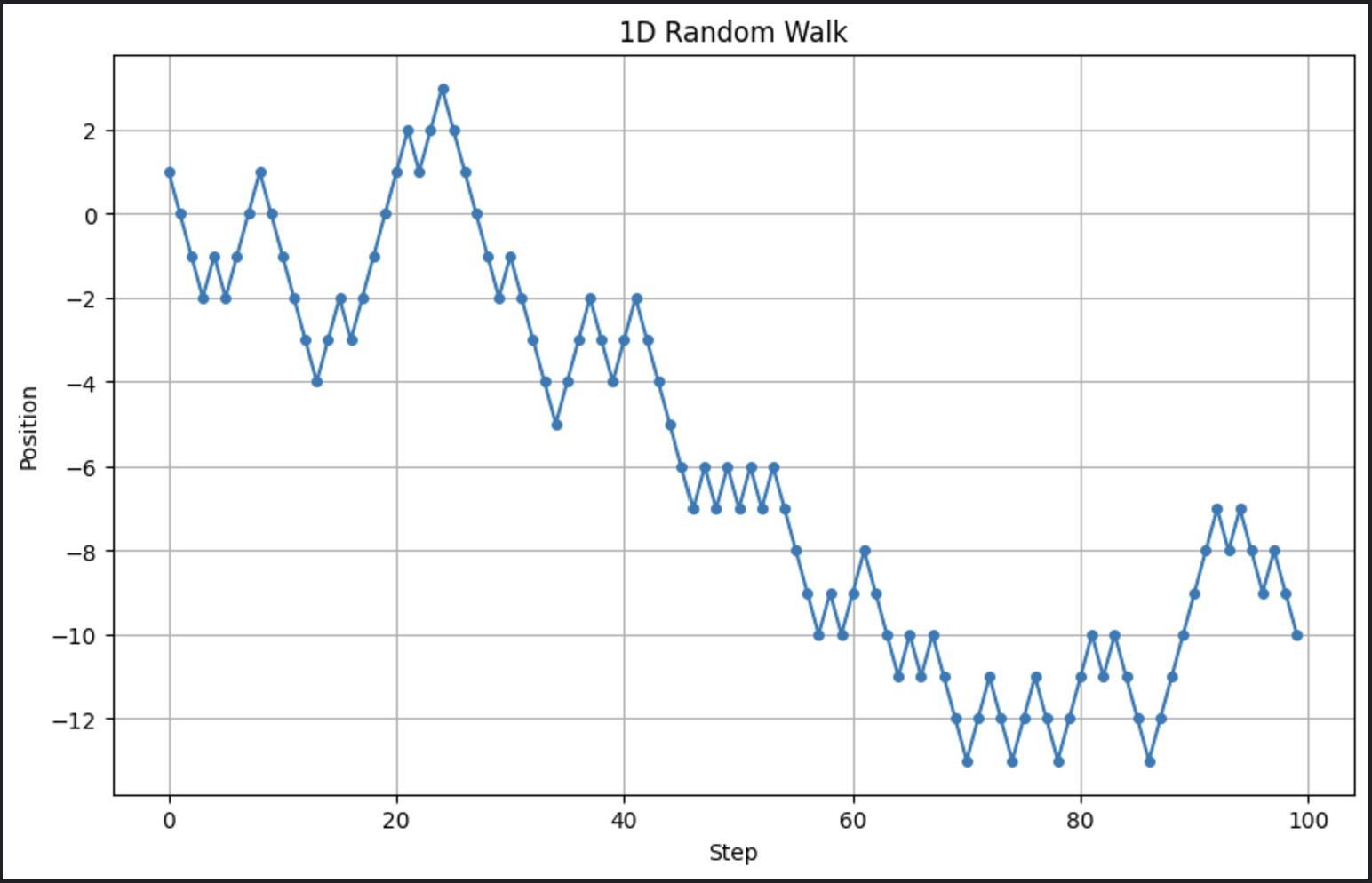
Теперь помните, что мы запускаем стохастическую модель. Это означает, что каждый раз, когда мы ее запускаем, вывод будет немного отличаться.
2D случайная прогулка
Теперь давайте расширим случайную прогулку до двух измерений. На каждом шаге направление будет выбираться случайным образом.
# Параметры n_steps = 500 # Генерация случайных шагов в направлениях x и y x_steps = np.random.choice([-1, 1], size=n_steps) y_steps = np.random.choice([-1, 1], size=n_steps) # Вычисление позиций x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Построение 2D случайной прогулки plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Красная точка для начала plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Черная точка для конца plt.title("2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Обеспечивает равномасштабное отображение по обеим осям plt.legend() plt.show()
Этот код создает визуально привлекательный путь в двух измерениях.
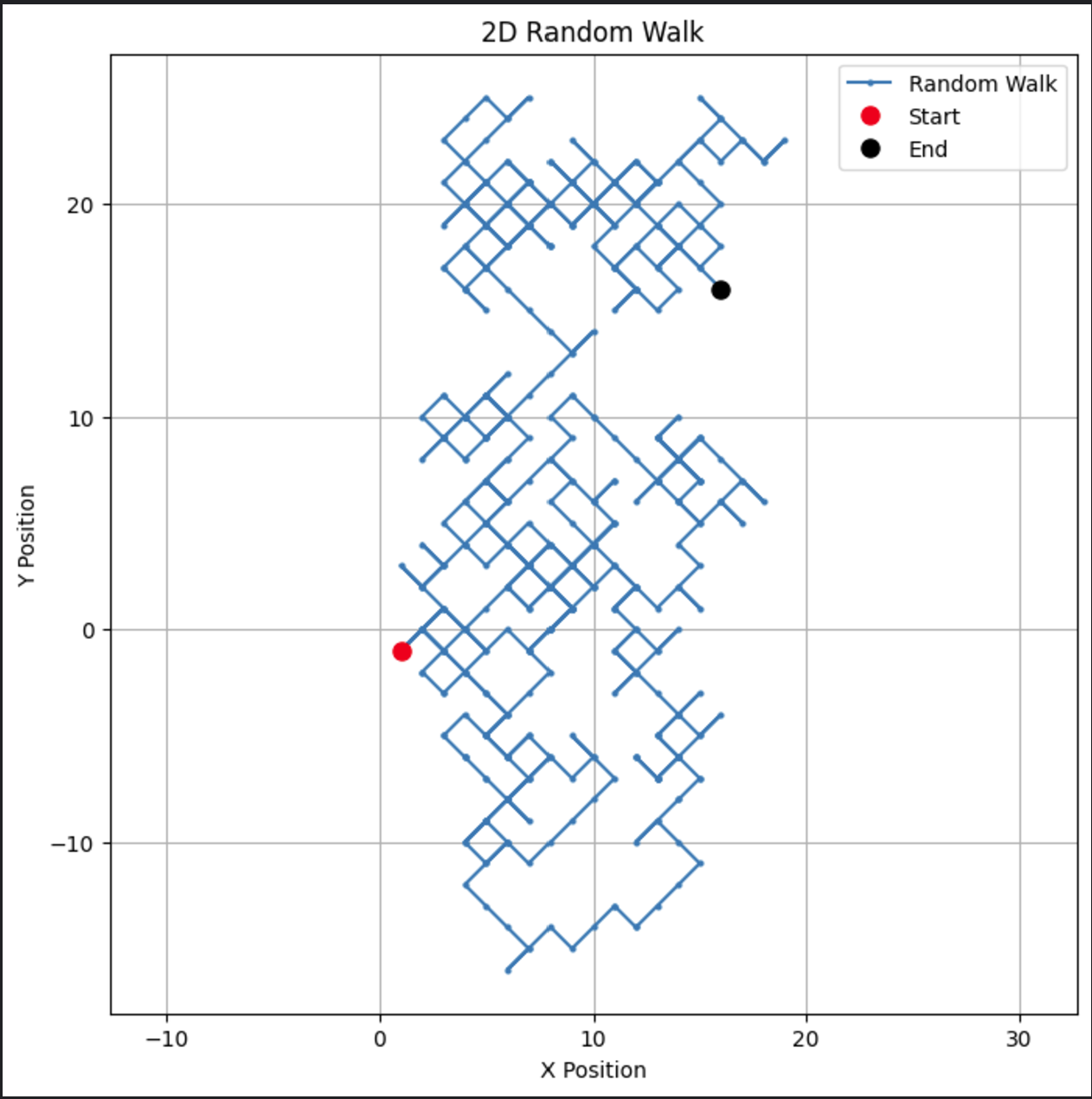
Этот тип двумерного случайного блуждания может быть изменен для применения в таких областях, как движение частиц или пространственное моделирование.
Смещенное случайное блуждание
Наконец, давайте рассмотрим немного более сложный пример: смещенное случайное блуждание. Чтобы ввести смещение, мы можем изменить вероятности каждого направления шага. Например, мы можем сделать вероятность шагов вверх более вероятной.
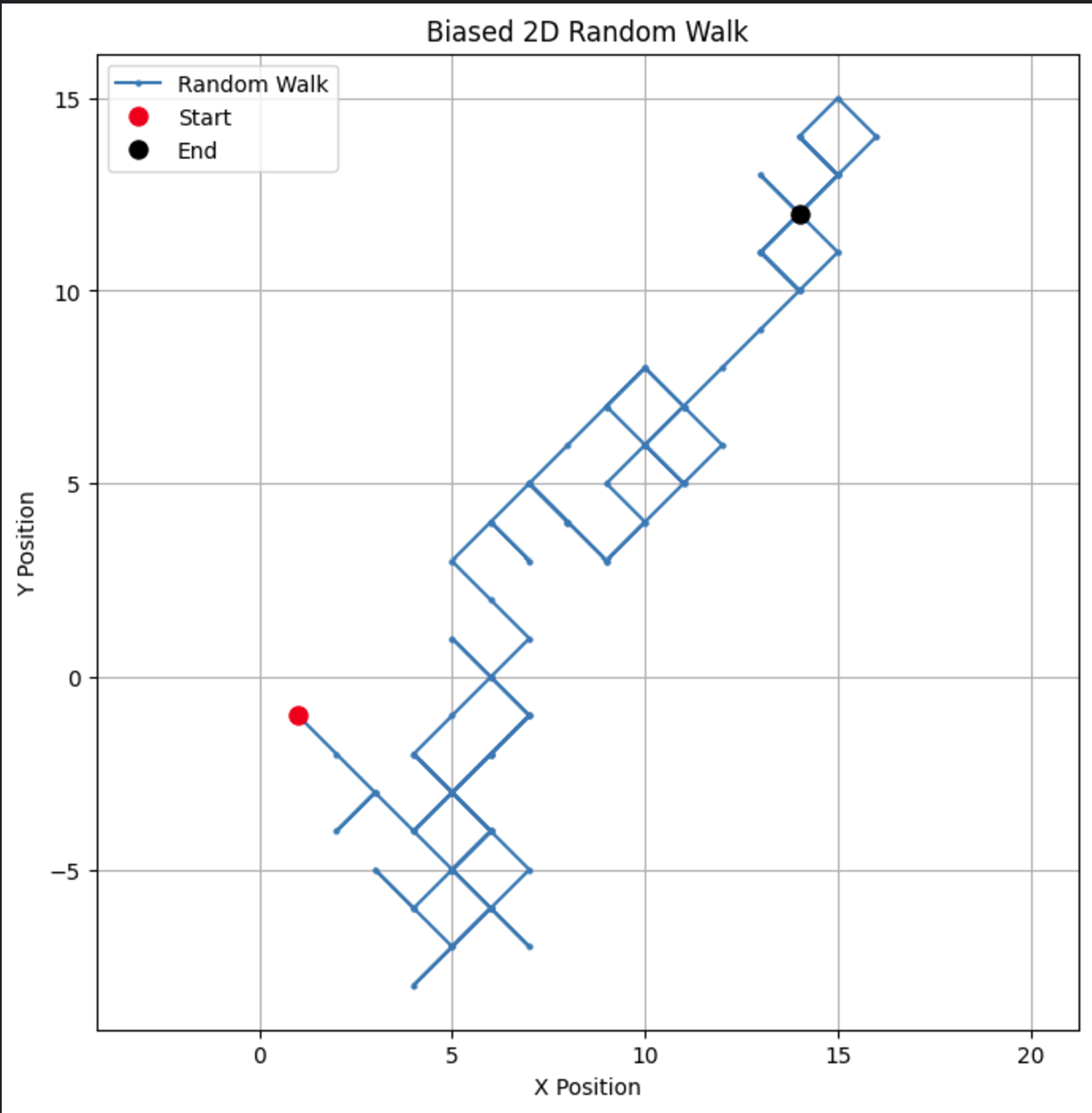
# Параметры n_steps = 100 bias = 0.7 # Вероятность сделать шаг +1 # Генерация смещенных случайных шагов по направлениям x и y x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias]) # Расчет позиций x_positions = np.cumsum(x_steps) y_positions = np.cumsum(y_steps) # Построение смещенного двумерного случайного блуждания plt.figure(figsize=(8, 8)) plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk') plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start') # Красная точка для начала plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End') # Черная точка для конца plt.title("Biased 2D Random Walk") plt.xlabel("X Position") plt.ylabel("Y Position") plt.grid(True) plt.axis('equal') # Обеспечивает одинаковое масштабирование для обеих осей plt.legend() plt.show()
Изменяя смещение, можно наблюдать, как ход имеет тенденцию к определенному направлению, имитируя реальные сценарии, такие как дрейф в ценах на акции или образцы миграции животных.
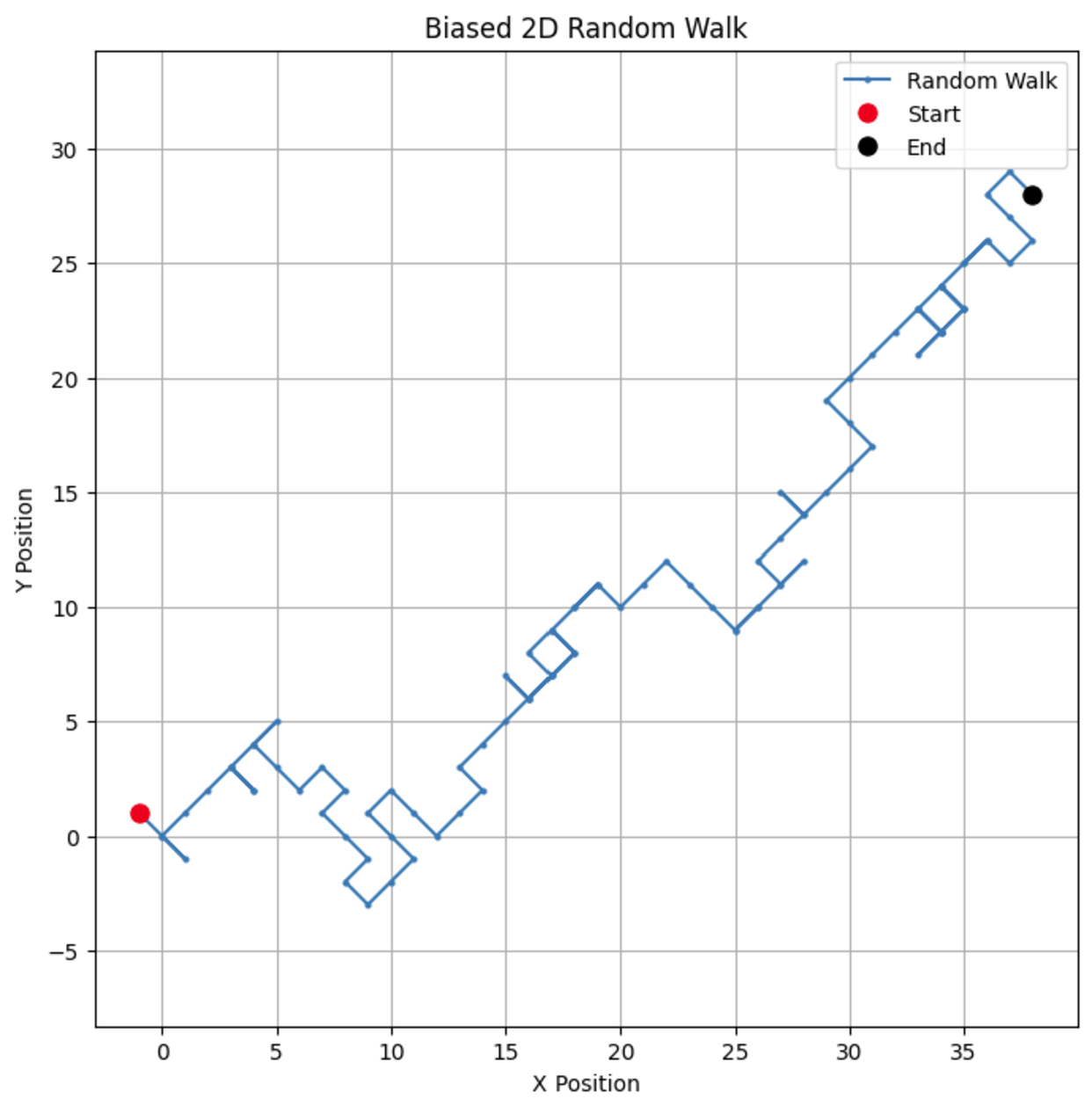
Если мы изменим параметр смещения на 0,55, мы увидим драматическую разницу в поведении модели. Хотя она все еще имеет предвзятость к движению вверх, смещение не такое сильное, что приводит к большему количеству петель и обходов.
Заключение
Случайные блуждания являются ценным инструментом моделирования для специалистов по данным, применимым в областях от физики до финансов и далее. Их способность моделировать сложные стохастические процессы делает их незаменимыми во многих реальных сценариях.
Хотите больше? Посмотрите набор курсов по вероятности и статистике от DataCamp. Здесь вы найдете множество отличных курсов как на Python, так и на R. Если вас интересует более продвинутый контент, обратите внимание на курс DataCamp по статистическому моделированию в Python и обучающий материал Введение в машинное обучение. Или если вы готовы проверить свои знания, попробуйте решить некоторые из этих задач по вероятности.













