שלב אחר שלב: חקירת המודל של צעד רנדומלי

בקורס הראשון שלי לסטטיסטיקה מבוססת קוד במכללה, המורה שלי הציע שאלה: איך נוכל למודד את התנועה הבראונית של חלקיק אבקה בודד בכלי עם מים? לאחר מספר ניסיונות לא מוצלחים, הגעתי עם חבריי לכיתה בסופו של דבר לתשובה הנכונה: הליכה אקראית. מאוחר יותר למדתי שהמודל הפשוט הזה משמש למודד כל מיני דברים, מהנעות של בעלי חיים ועד לתנודות במחירי מניות.

במאמר הזה, נחקור את היסודות המתמטיים של הליכות אקראיות, נבחן סוגים שונים, ונדון ביישומים שלהם. חלק ממה שהופך את ההליכה האקראית למעניינת הוא שהיא משמשת כל כך הרבה תחומים שונים. בנוסף לדוגמה שלי, בפיזיקה, זה עוזר לתאר את תנועת החלקיקים; במימון, זה מודד את תנודות מחירי המניות; ובביולוגיה, זה מסביר את דפוסי התנועה של בעלי חיים. הליכות אקראיות תופסות את האקראיות של העולם האמיתי, מה שחשוב לסימולציה של תהליכים סטוכסטיים.

עבור אלה שמחפשים לבנות בסיס חזק בסטטיסטיקות שעומדות בבסיס תאוריית הצעד האקראי, אנו ממליצים להתחיל עם הקורס Introduction to Statistics in R או עם הקורס Introduction to Statistics in Python.

מהן הצעדים האקראיים?

בתוריית ההסתברות, צעד אקראי הוא מודל המתאר רצפי צעדים אקראיים המהווים נתיב. או שנוכל לומר שצעד אקראי הוא מודל מתמטי המתאר נתיב שנוצר על ידי רצף של צעדים, כאשר כל צעד מוחלט באופן עצמאי ועם סיכוי מסוים. הסטוכסטיקה הזו הופכת את הצעדים האקראיים לאפייניים לא ניתני תחזייתיות.

דמיינו אדם שעושה צעד בכיוון אקראי בכל רגע. במהלך הזמן, הנתיב שלו מתקיים כנתיב מבלבל ולא ניתן לחזאות. למרות פשטותה, המושג הזה מסתיר עומק וגמישות מדהימים, מייצג תרחישים שונים בעולם האמיתי שכוללים אקראיות.

הסבר קונספטואלי של צעד רנדומלי. תמונה באדיבות napkin.ai.

רעיון הצעדים הרנדומליים חוזר ללימודי עניין בהתפלגות הסתברותית בתחילת הדרך. אחד הדוגמאות המוקדמות, המכונה לעיתים "צעד השיכור", ממחישה כיצד אדם הולך בצעדים באופן רנדומלי יתהפך בצורה בלתי צפויה במקום להתקדם בצורה חסומה ליעד. הרנדומיות הזו, בשילוב עם הנחה שכל צעד הוא תלוי באופן עצמאי בצעדים קודמים, הקימה את יסודות דגמי הצעד הרנדומלי המודרניים.

הבנת המתמטיקה של צעדי רנדום

כדי להבין צעדי רנדום, בואו נתחיל עם מקרה פשוט: צעד רנדומלי חד-מימדי (1D).תיאמו חלקיק על ציר המספרים. הוא יכול לזוז בין +1 ו-1 לאורך קו המספרים בכל צעד. כל צעד נקבע על ידי סיכוי שווה לזוז ימינה או שמאלה. במהלך הזמן, מיקום החלקיק יוצר תפיצות סבירות שמתפשטת, המייצגת את הסתברות מציאתו במקומות שונים.

העקרון הזה יכול להתרחש בשתי או שלוש מימדים. בהליכה אקראית דו-ממדית (2D), החלקיק זז על מישור ויכול לצעוד באחת מארבעת הכיוונים הראשיים (למעלה, למטה, שמאלה, ימינה) בסיכוי שווה. באופן דומה, בהליכה אקראית שלושת הממדים (3D), החלקיק זז במרחב ויכול לצעוד באחד מששת הכיוונים האפשריים (למעלה, למטה, שמאלה, ימינה, קדימה, אחורה) בסיכוי שווה. ההליכות האקראיות בממדים גבוהים אלו מתעסקות עם תרחישים עוד מורכבים וממציאים יותר.

מאפיין מובהק של הליכות אקראיות הוא הטבע הסטוכסטי שלהן, כלומר כל צעד תלוי רק במיקום הנוכחי ולא בצעדים הקודמים. זה מהווה סוג של תהליך מרקוב—עקרון מתמטי כפי שהמצב העתידי תלוי רק במצב הנוכחי, ולא בסדר האירועים שקדמו לו. התנועה "חסרת זיכרון" הזו, בשילוב עם התפלגויות סבירות המתארות מיקומים אפשריים, מספקת יסוד מתמטי סולידי להבנת הליכות אקראיות.

ניתן לנתח צעד רנדומלי באמצעות מאפיינים סטטיסטיים כדי להבין את ההתנהגות שלו לאורך זמן. כך ניתן לבדוק אספקטים כמו המרחק הצפוי מנקודת ההתחלה, חלוקת הסתברות של התפקודים האפשריים, והסיכוי לחזור למוצא. הניתוחים הללו עוזרים לנו לכמת את האקראיות והניבוי, לספק תובנות בתבניות, ולבצע חיזויים.

מאפיינים מרכזיים של צעדים רנדומליים

צעדי רנדומליים מציעים מאפיינים חשובים שמסייעים לנו להבין את ההתנהגות והיישומים שלהם. הנה כמה נקודות מרכזיות לשקול:

ציפיות ושונות

בצעד רנדומלי חד-ממדי, ניתן לחשב את המרחק הצפוי (או המיקום הממוצע) מנקודת ההתחלה לאורך זמן. אם כל צעד יש סיכוי שווה להזוז שמאלה או ימינה, המיקום הצפוי לאחר מספר גדול של צעדים נשאר אפס, מה שמרמז על כך שבממוצע, הלוך על המקור.

עם זאת, השונות של המיקום, המודדת את התפשטות או הפיזור של מיקומים אפשריים, גדלה עם כל צעד. ספציפית, בהליכה רנדומלית סימטרית, השונות גדלה באופן ליניארי עם מספר הצעדים, מה שהופך אותה לאינדיקטור שימושי של המרחק הטיפוסי מהמקור לאורך זמן.

אוטוקורלציה

בעוד שהליכי רנדום פשוטים אינם מציגים קורלציה בין צעדים (כל צעד הוא עצמאי מהאחרון), סוגים מסוימים של הליכות רנדומליות מביאים לאוטוקורלציה, שבה צעדים קודמים יכולים להשפיע על צעדים עתידיים. לדוגמה, בהליכה רנדומלית עם הטיה, צעדים עשויים להיות בעלי נטייה קלה בכיוון אחד, מה שגורם למיקומים להיות יותר צפויים.

האוטוקורלציה בהליכה רנדומלית משפיעה על איך אנו מודלים וחוזים את התקדמות ההליכה. זה במיוחד רלוונטי ביישומים שבהם התנהגות קודמת משפיעה על צעדים עתידיים, כמו במודלים פיננסיים מסוימים.

תיאוריית הגבול המרכזי

המשפט המרכזי של הממוצעים (CLT) מסביר לנו כי סכום של מספר גדול של משתנים רנדומליים תופס גישה של התפלגות נורמלית (או גאוסית), בלתי תלוי בהתפלגות המקורית. בהקשר של צעדי רנדום, זה אומר כי ככל שמספר הצעדים עולה, ההתפלגות של המיקומים מתקרבת להתפלגות נורמלית. זוהי מאפיין שימושי מכיוון שזה מאפשר לנו לאפרוק את ההסתברות למציאת הלוחץ במרחקים מסוימים מנקודת ההתחלה.

חוק הממספרים הגדולים

חוק הממספרים הגדולים (LLN) מסביר כי ככל שמספר הניסויים או הצעדים עולה, ממוצע התוצאות מתכנס לממוצע האמיתי. בצעדי רנדום, זה אומר כי בעוד המיקום הממוצע נשאר אפס, השונות והטווח של המיקומים האפשריים גדלים באופן צפוי עם כל צעד נוסף. עקרון זה עוזר לגשר על הפער בין האקראיות הטהורה והתבניות הסטטיסטיות הניתנות לניבוי בדגמים גדולים.

סוגי צעדי רנדום

הליכות אקראיות משתנות במידה ניכרת בהתאם לחוקים השולטים בכל צעד. סוגים אלה משפיעים על אופן ההתנהגות של ההליכה. חלקם מיועדים לסביבות פשוטות או מובנות בעוד אחרים מצוידים לתופעות מורכבות יותר מהעולם האמיתי. בואו נחקור כמה מהסוגים הנפוצים ביותר של הליכות אקראיות.

הליכות אקראיות ב-1D, 2D ו-3D

הממדיות של הליכה אקראית משחקת תפקיד בסיסי בהתנהגות שלה. בהליכה אקראית ב-1D, כל צעד הוא או תנועה קדימה או תנועה אחורה לאורך קו. זה מקל על המודל והניבוי של ההליכה.

עם זאת, כאשר אנו עוברים להליכות ב-2D (מישור) וב-3D (חלל), האפשרויות להליכי הליכה גדלות בצורה משמעותית, ומביאות להתנהגות חדשה. לדוגמה, בהליכה אקראית ב-2D, הסיכוי לחזור לנקודת ההתחלה נשאר גבוה, בעוד שבהליכה אקראית ב-3D, הסיכוי הזה פוחת.

השינוי הזה חשוב בתחומים כמו פיזיקה וכימיה, שם חלקיקים עשויים להתפשט באופן שונה בהתאם להגבלות ממדיות.

הליכה אקראית ברשת

בהליכה אקראית ברשת, התנועה מוגבלת לנקודות דיסקרטיות על רשת או רשת. סוג זה של הליכה נפוץ בפיזיקה ובתאוריית רשתות, שבהן הצמתים מאוחסנים ברשת, והתנועה יכולה להתרחש רק לצמתים שסמוכים.

דוגמה נפוצה היא רשת דו-ממדית, שבה כל צעד מאפשר תנועה לנקודות שסמוכות על רשת קרטזית. ההגבלה הזו מפשטת את המודלים על ידי הגבלת נתיבי תנועה, מה שמועיל בדמיות של רשתות מורכבות או מבני מולקולות.

הליכה אקראית גאוסית

בהליכת ווק רנדומלי גאוסי, גודל כל צעד נקבע על ידי התפלגות גאוסית (או נורמלית). במקום לנוע במרחק קבוע, גודל הצעד משתנה לפי התפלגות בצורת פעמון, כאשר רוב הצעדים קטנים וקיימים קפיצים גדולים לעיתים. סוג זה של הליכה נמצא בשימוש תדיר במודלים פיננסיים כדי לקחת בחשבון את השונות בשינויים במחירי נכסים.

הליכות רנדומליות הטרוגניות ומוטות

הליכות רנדומליות הטרוגניות ומוטות מאפשרות שונות בכיוון ובגודל הצעד בהתאם לסיכויים מסוימים. גמישות זו הופכת אותן ליותר מתאימות לתרחישים מהעולם האמיתי.

בהליכת ווק רנדומלי הטרוגני, הסיכוי לנוע בכל כיוון עשוי להשתנות בהתאם למיקום או לתנאים חיצוניים. לדוגמה, בעלי חיים שמחפשים מזון עשויים להעדיף אזורים עם משאבים ידועים, מה שמייצר הליכת רנדומלית מוטה. הליכות אלו מועילות ללימוד התנהגויות שתלויות בגורמים הקשריים.

הליכה רנדומלית עם דריפט

בהליכה אקראית עם הטיית תנועה, קיימת מגמה קבועה להתקדם בכיוון אחד. לדוגמה, מחירי המניות עשויים להציג טרנד כללי של עלייה לאורך הזמן למרות הנפילות היומיומיות. הטיית התנועה במהלכים אלו מייצגת כוח חיצוני או טרנד שמשפיע על הנתיב. סוג זה נראה לעתים תכופות בעולם הפיננסי, שם המודלים משתמשים במונח הטיית תנועה כדי לייצג צמיחה או ירידה, ומספקים גישה יותר ריאליסטית לחזית מחירי הנכסים וטרנדים שוק.

כל אחד מסוגי ההליכה האקראית הללו משרת מטרה ייחודית, מציע דרכים שונות לחידוד ההתנהגות האקראית, עם מבנה. האילוצים הממדיים, ההפצה של הצעדים, והטיית התנועה או הקידה מפכים את ההליכות האקראיות לכלי גמיש מאוד למודלים נתונים ולסימולציה בכל תחום.

יישומים ממומשים של הליכות אקראיות

הליכות אקראיות הן לא רק בניינים תיאורטיים; הן משמשות תפקיד חיוני ביישומים מעשיים רבים במגוון תחומים. בואו נשקול כיצד הליכות אקראיות מסייעות בפתרון בעיות בפועל בתחומים שונים.

יישומים במדעי הנתונים ולמידת מכונה

מדעי המחשב

הליכות אקראיות מהוות בסיס למספר אלגוריתמים במדעי המחשב, כגון דגימה אקראית, חיפוש בגרף האינטרנט וסגמנטציה של תמונות. לדוגמה, אלגוריתם PageRank של גוגל השתמש בהליכי אקראיות כדי לדרג דפי אינטרנט לפי הרלוונטיות שלהם, תוך סימולציה של איך משתמש עשוי לנווט באופן אקראי בין קישורים באינטרנט.

חילוץ תכונות

בלמידת מכונה, הליכות אקראיות יכולות לסייע בחילוץ תכונות על ידי הדגשת קשרים בין נקודות נתונים. לדוגמה, בניתוח רשתות, הליכות אקראיות יכולות לחשוף אשכולות או קהילות, ולסייע במשימות כמו מערכות המלצה וניתוח רשתות חברתיות.

זיהוי אנומליות

הליכות אקראיות יכולות גם לשמש לזיהוי אנומליות בסטי נתונים. לדוגמה, אם נקודות נתונים סוטות באופן משמעותי מדרך טיפוסית במודל הליכה אקראית, נקודות אלו עשויות להעיד על אירועים לא רגילים או שגיאות בנתונים. זיהוי אנומליות הוא בעל ערך במיוחד בתחומים כמו אבטחת סייבר וגילוי הונאות.

סימולציה של תהליכים סטוכסטיים

הליכות אקראיות מדמות תהליכים סטוכסטיים, או תהליכים שהוגדרו באקראי, ומאפשרות למדעני נתונים לדגם תופעות בלתי צפויות מהעולם האמיתי. על ידי סימולציה של הליכות אקראיות, אנו יכולים לקבל תובנות על מערכות שבהן חיזוי מדויק הוא אתגר, כמו דפוסי מזג האוויר או התנהגות לקוחות.

חיזוי סדרות זמן

בניתוח סדרות זמן, הליכות אקראיות מהוות את הבסיס לדגמים מסוימים של חיזוי, כולל ההנחה על הליכת אקראית במימון. מודלים אלה מניחים כי הערכים העתידיים בסדרת זמן תלויים אך ורק בערך האחרון, ללא קשר למגמות העבר.לפרטים נוספים על חיזוי סדרות זמן, בדקו את ARIMA לחיזוי סדרות זמן: מדריך מקיף. כמו כן, קחו את הקורס שלנו חיזוי ב-R עם פרופסור היינדמן, שמקשר מודלים של הליכות אקראיות לשיטות חיזוי נאיביות ונאיביות עונתיות.

יישומים בתחומים אחרים

מימון

אחת השימושים המצטיינים ביותר של הליכות אקראיים היא בדיגיטל מודלינג, בעיקר לצורך חיזוי מחירי המניות. ההשקעה בשוק מופיעה ומחירי המניות בעצם אקראיים, כשמידע חדש מוטמע מיד, עשוי מחירים עתידיים שאי-אפשר לחזות. הליכות אקראיים יכולים לשמש למודל תהליכי שינוי במחירי המניות לאורך זמן, ממחישים איך מחירים מתנדנדים בלי נתיב צפוי.

מתמטיקה

במתמטיקה טהורה, הליכות אקראיים מספקות פתרונות לבעיות מורכבות. למשל, הן שימושיות בפתרון משוואת לפלס, בניתוח רשתות ובחקירת קומבינטוריקה.

פיזיקה וכימיה

במדעי הטבע, הליכות אקראיים מרכזיות למודלים של תהליכי התפשטות, כגון דרכם של חומרים באמצע. תנועת בראונית, שבה חלקיקים תלויים בנוזל זזים באופן לא צפוי עקב התנגשויות עם חומרים סביבתיים, היא דוגמה קלאסית שניתן לדמות באופן מדויק באמצעות הליכות אקראיים. בכך ממוצעת הליכות זו למדתי בפועל ראשונית.

ביולוגיה

הליכות אקראיים חשובים באקולוגיה ללימוד דפוסי תנועה של בעלי חיים. בעלי חיים שמחפשים משאבים עשויים לנראות כאילו נעים בהליכה אקראית, לפעמים עם הטייה לאזורים עם משאבים ידועים. עקרונות ההליכה האקראית יכולים לשמש גם לדמות מושגים ביולוגיים אחרים, כגון התפשטות אוכלוסיות או גנים, ולעיתים קרובות ניתן לדמות אותם בעקרונות ההליכה האקראית, מה שהופך קל יותר להבין ולחזות שינויים באקוסיסטמות.

מקרים מיוחדים וגרסאות שונות של הליכות אקראיות

בנוסף להליכה האקראית הקלאסית, קיימות מספר גרסאות מתקדמות שמרחיבות את המושג כדי להתאים ליישומים מותאמים.

הליכות שממנות עצמן

הליכה שממנה את עצמה היא הליכה אקראית שבו הנתיב אינו משוב לכל עמדה שכבר עבר עליה. גרסה זו מיוחדת ושימושית במיוחד בתחומים כמו כימיה של פולימרים, שבה ניתן לדמות כיצד שרשראות הפולימר נוצרות בלע צלב אחת את השנייה. בשל כך שכל צעד ממנה את הנקודות שכבר נכנסו אליהן, הליכות שממנות עצמן מוגבלות יותר מהליכות אקראיות קלאסיות. זה אומר שהן מאתגרות מבחינה חישובית אך שימושיות להבנת נתיבים לא מכסים במרחבים מצומצמים.

סניפות

בצעדי הליכה אקראית המפוצלת, הנתיב יכול להתפצל לכמה ענפים, עם כל ענף נוסף שעליו נעקבת הליכה אקראית. סוג זה של הליכה חשוב במודלים של תהליכי פיצול כמו התחלקות תאים או פיזור מידע דרך רשתות. כל "ענף" מייצג נתיב אקראי עצמאי שמתפוצל ממקור משותף.

הליכות מקורלים

הליכות מקורלים מעבירים את המושג הזה צעד קדימה, כאשר כיוון כל צעד נמען חלקית על ידי הצעד הקודם. משתנה זה יעיל למודלים שבהם שינויים מתרחשים באופן בדרך כלל באופן הדרגתי ולא אקראי. הליכות מקורלים מיושבים לעיתים קרובות בתחומים כמו כלכלה לדמות מגמות מחירים או באקולוגית תנועה להבין איך בעלי חיים ניווטים בסביבותיהם עם זיכרון מכיוון העבר שלהם.

הליכות בלי לולאות

הליכה בלי לולאות היא נוסחה שבה לולאות, או נתיבים שחותכים את עצמם, מוסרים בזמן צורת חיובית. בכל פעם שצעד מחדש מבקר במיקום, הלולאה המערבת נמחקת, משאירה נתיב משוטף, לא מחזורי. הליכות בלי לולאות מיושבות באופן נפוץ בניתוח רשתות ואלגוריתמי יצירת מבוך מכיוון שהן יוצרות נתיבים שממנעים דומהות.

יישום צעדי רנדום בפייתון

בואו ננסה ליישם צעד רנדומלי בפייתון.כדי להתחיל, וודאו שיש לכם את פייתון מותקן (נשתמש בפייתון 3.10) ואת הספריות הנחוצות זמינות. ניתן להתקין ספריות חסרות בעזרת pip. הנה מה שנצטרך:

import numpy as np # לפעולות מספריות ויצירת צעדים רנדומליים
import matplotlib.pyplot as plt # לעיבוד נתונים והצגת הצעדים הרנדומליים

צעד רנדומלי ב-1 ממד

נתחיל עם צעד רנדומלי חד-ממדי פשוט, כאשר כל צעד הוא או +1 או -1, בחירה רנדומלית.

# פרמטרים
n_steps = 100  # מספר הצעדים

# יצירת צעדים רנדומליים: +1 או -1
steps = np.random.choice([-1, 1], size=n_steps)

# חישוב עמדות
positions = np.cumsum(steps)

# עיצוב הצעד הרנדומלי
plt.figure(figsize=(10, 6))
plt.plot(positions, marker='o', linestyle='-', markersize=4)
plt.title("1D Random Walk")
plt.xlabel("Step")
plt.ylabel("Position")
plt.grid(True)
plt.show()

זה יוצר צעד רנדומלי פשוט ומחזיר את ההתקדמות במהלך הזמן. הנה הפלט כאשר אני מריץ את הקוד:

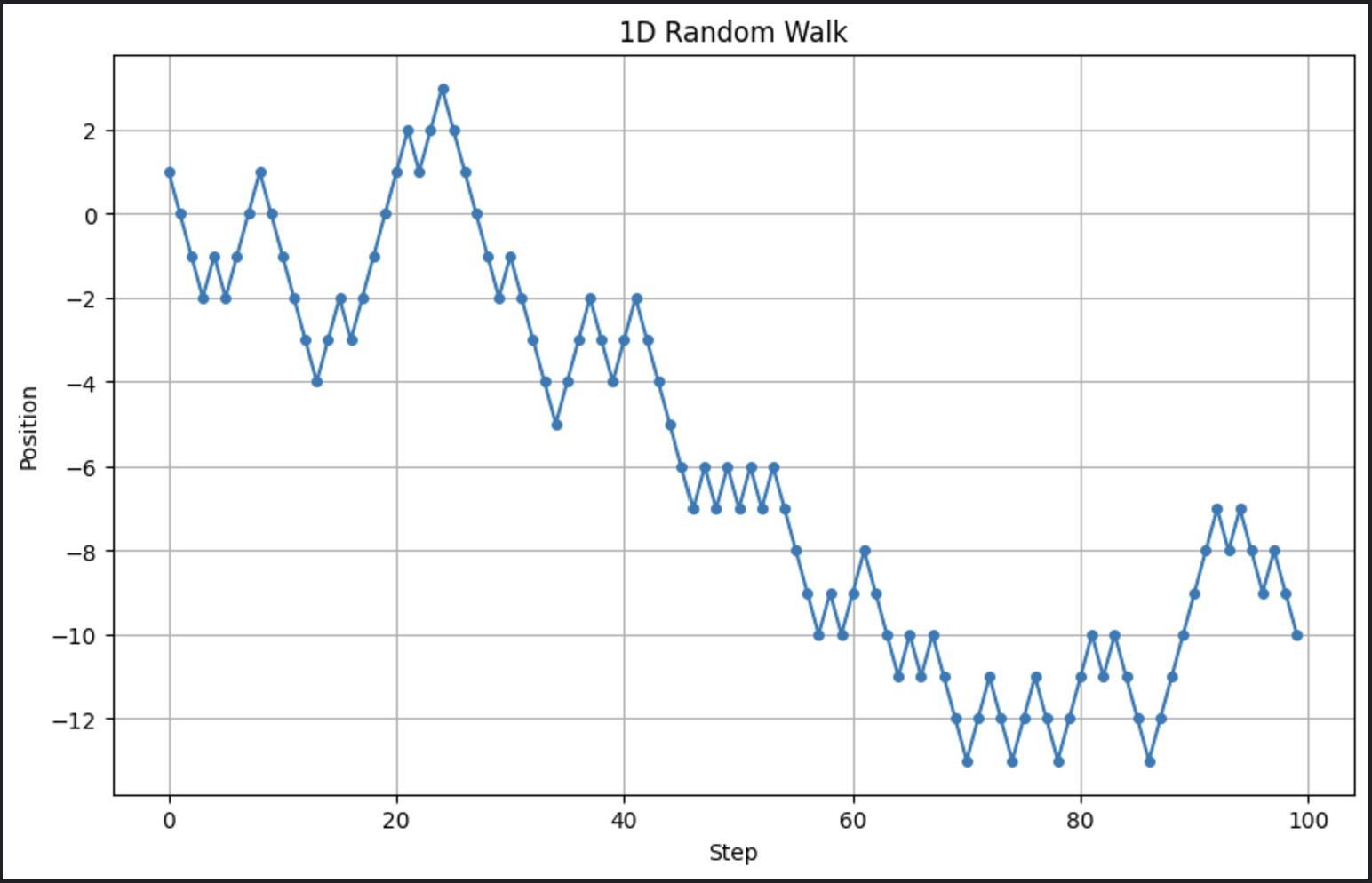
זכור, אנחנו מריצים מודל סטוכסטי. זה אומר שבכל פעם שנריץ אותו, הפלט ייראה קצת שונה.

צעד רנדומלי ב-2D

כעת נרחיב את הצעד הרנדומלי לשתי מימדים. בכל צעד, הכיוון ייבחר באופן רנדומלי.

# פרמטרים
n_steps = 500

# יצירת צעדים אקראיים בכיוון x ו-y
x_steps = np.random.choice([-1, 1], size=n_steps)
y_steps = np.random.choice([-1, 1], size=n_steps)

# חישוב עמדות
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# עיצוב הצעד הרנדומלי ב-2D
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # נקודה אדומה להתחלה
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # נקודה שחורה לסיום
plt.title("2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # מבטיח קנייה שווה לשני הצירים
plt.legend()
plt.show()

קוד זה יוצר מסלול חזותי מעניין בשני ממדים.

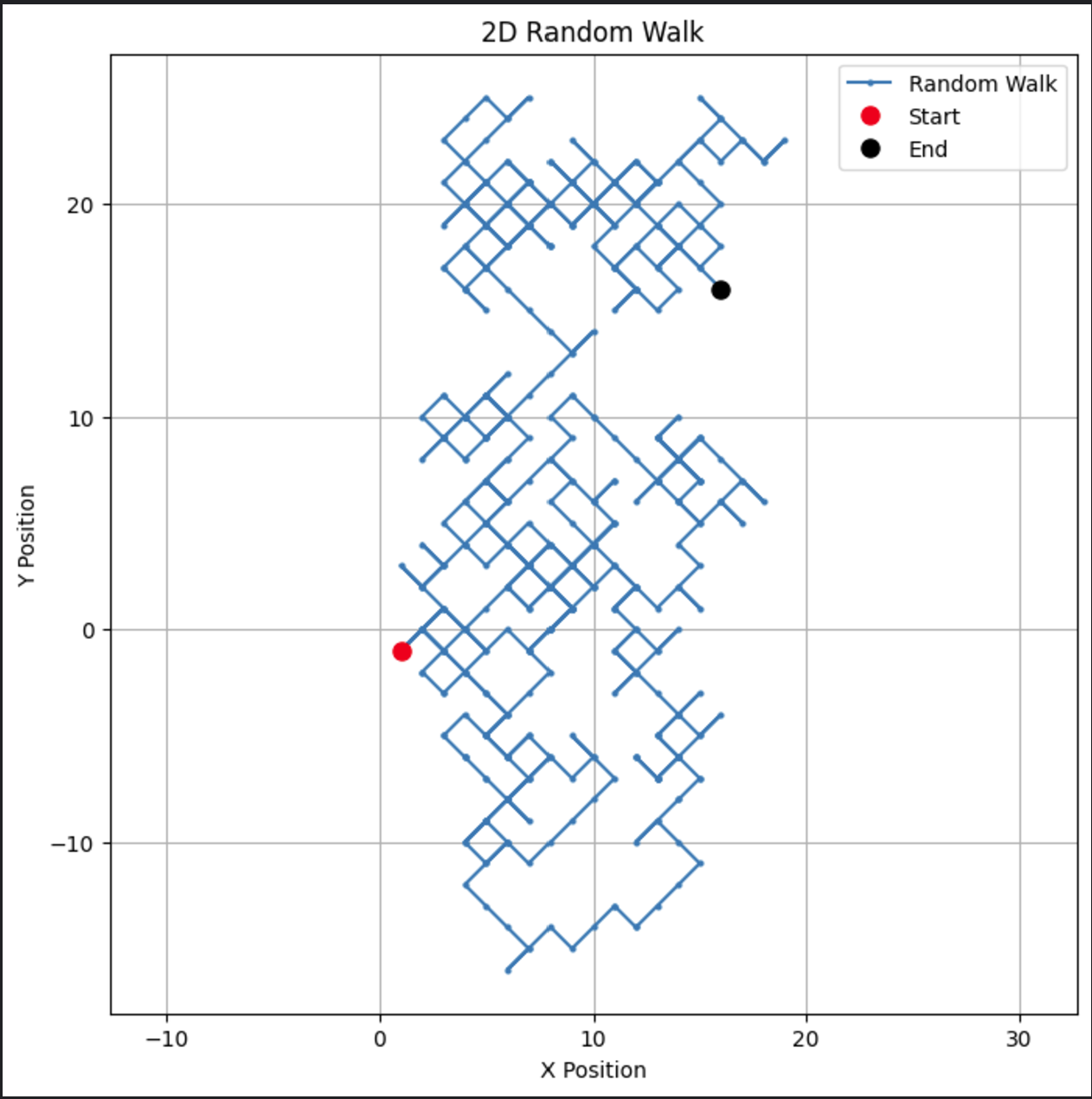
סוג זה של הליכה רנדומלית דו-ממדית יכול להיות מותאם ליישומים כמו תנועת חלקיקים או מודליזציה מרחבית.

הליכה רנדומלית מעודפת

לבסוף, נבחן דוגמה מעט יותר מורכבת: הליכה רנדומלית מעודפת. כדי להציג הטיה, אנו יכולים להתאים את ההסתברויות של כל כיוון צעד. לדוגמה, ייתכן שנגרום לצעדים כלפי מעלה להיות סבירים יותר.

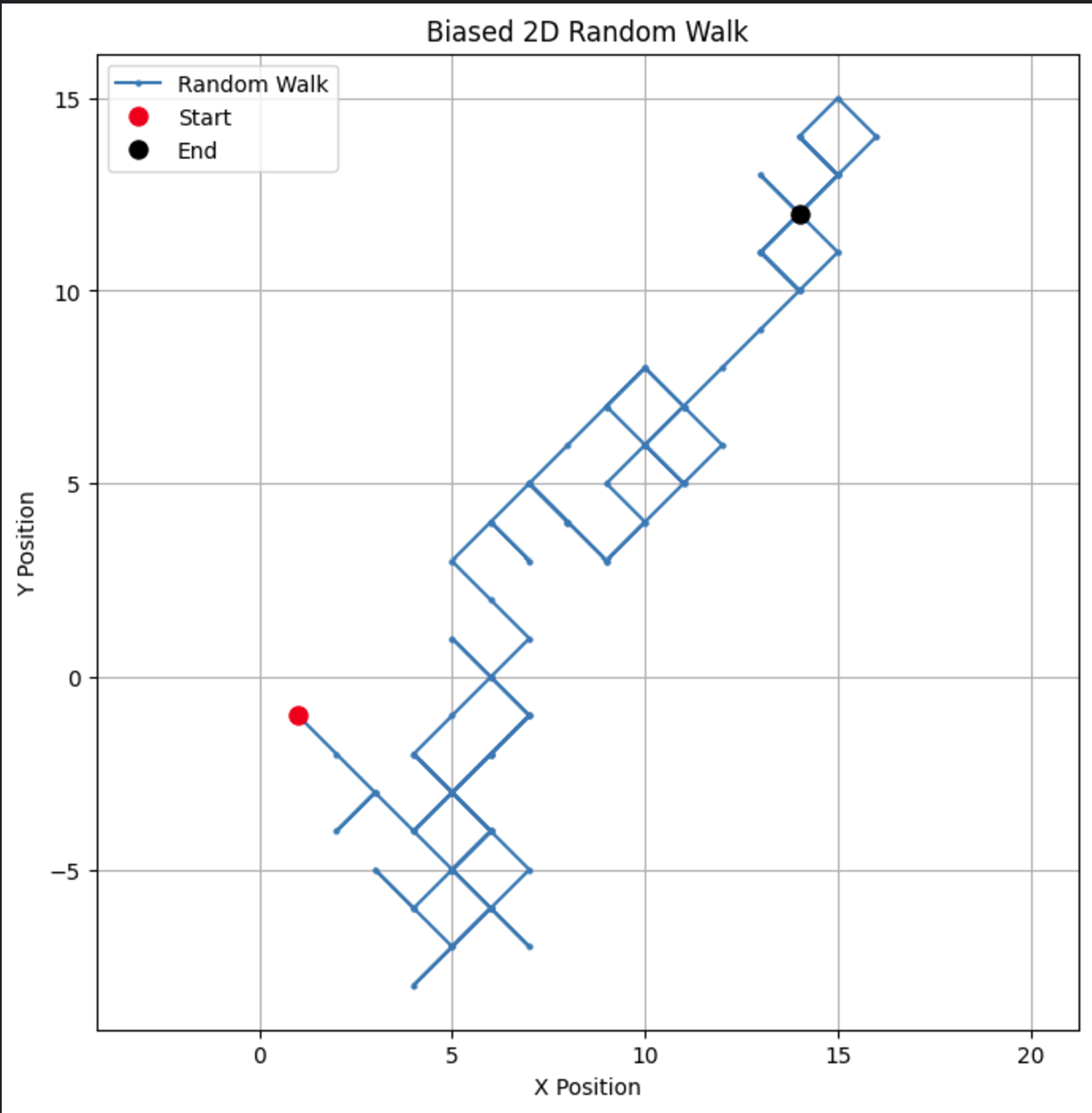
# פרמטרים
n_steps = 100
bias = 0.7  # הסתברות של צעידה +1

# לייצר צעדים רנדומליים מעודפים בכיווני x ו-y
x_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])
y_steps = np.random.choice([-1, 1], size=n_steps, p=[1-bias, bias])

# לחשב מיקומים
x_positions = np.cumsum(x_steps)
y_positions = np.cumsum(y_steps)

# לצייר את ההליכה הרנדומלית המעודפת ב-2D
plt.figure(figsize=(8, 8))
plt.plot(x_positions, y_positions, marker='o', linestyle='-', markersize=2, label='Random Walk')
plt.plot(x_positions[0], y_positions[0], 'ro', markersize=8, label='Start')  # נקודה אדומה להתחלה
plt.plot(x_positions[-1], y_positions[-1], 'ko', markersize=8, label='End')  # נקודה שחורה לסיום
plt.title("Biased 2D Random Walk")
plt.xlabel("X Position")
plt.ylabel("Y Position")
plt.grid(True)
plt.axis('equal')  # מבטיח סקלינג שווה לשני הצירים
plt.legend()
plt.show()

על ידי שינוי ההיטל, ניתן לראות איך ההליכה נטה לטובת כיוון מסוים, סימולציה של תרחישים בעולם האמיתי כמו התרעשות במחירי המניות או דפוסי הגירות של בעלי חיים.

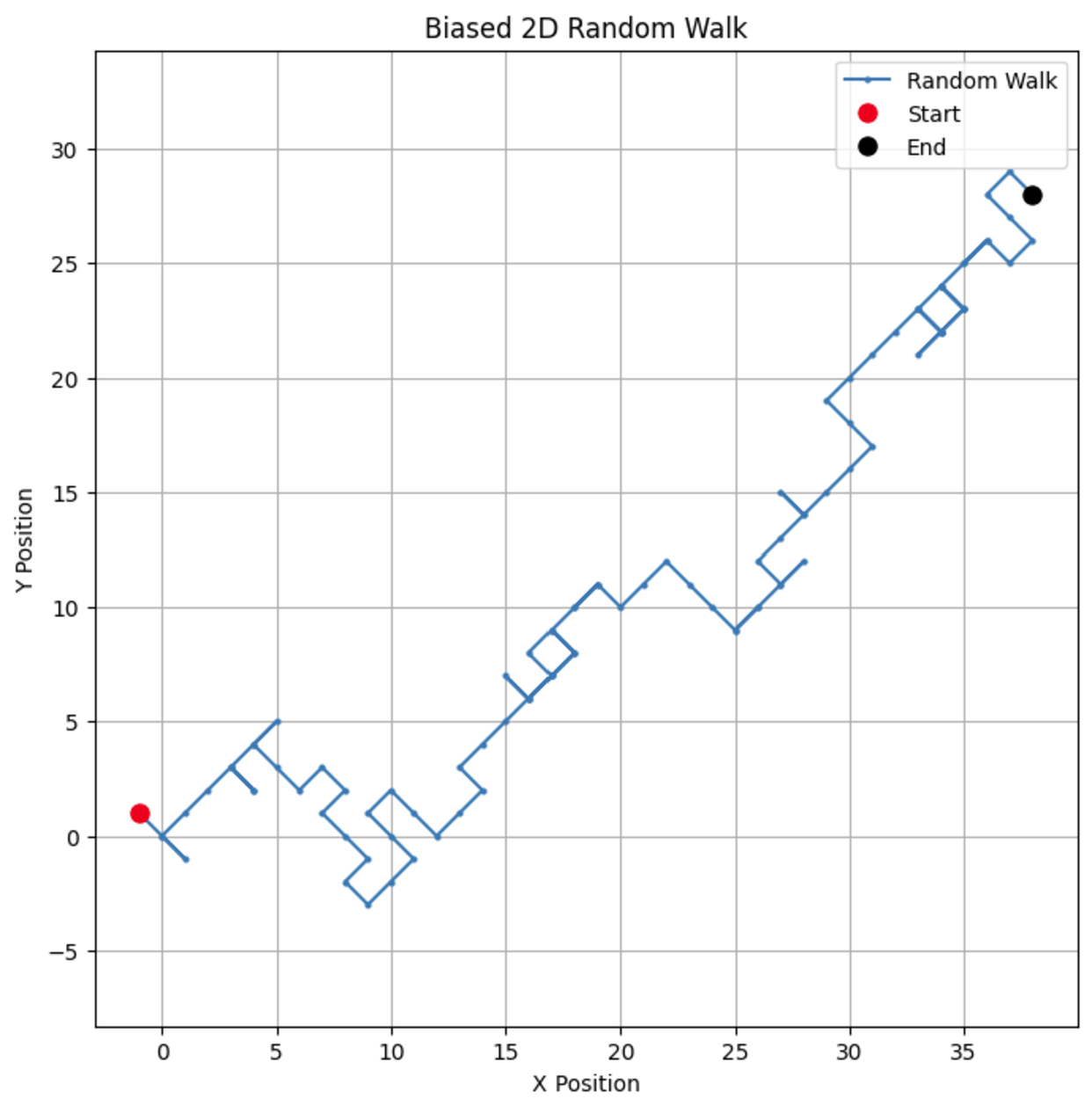
אם נשנה את פרמטר ההיטל ל-0.55, ניתן לראות הבדל מרשים בהתנהגות המודל. בעוד שיש לו עדיין היטל לעלות, ההיטל אינו כה חזק, מה שמביא לפליטות ולסיבובים נוספים.

מסקנה

הליכות אקראיות הן כלי דמודלציה יקר של מדעני נתונים, שימושיים בתחומים מפיזיקה ועד פיננסים ומעבר להם. יכולתם לדמות תהליכים מורכבים סטוכסטיים הופכת אותם לבלתי נמנעים בתרחישים רבים בעולם האמיתי.

רעב לעוד? בדוק את אוסף קורסי ההסתברות והסטטיסטיקה של DataCamp. תמצא קורסים נהדרים בשפת פייתון ו-R. אם אתה מעוניין בתוכן מתקדם יותר, בדוק את הקורס של DataCamp על סימולציות סטטיסטיות בפייתון ואת המדריך המבוא ללמידת מכונה. או אם אתה מוכן לבחון את ידעך, עסוק בכמה מ-פאזלי ההסתברות אלו.