Самоорганизующиеся карты: Интуитивное руководство с примерами на Python

Настройка окружения для SOM

Перед созданием SOM нам необходимо подготовить окружение с необходимыми пакетами.

Установка библиотек Python

Нам нужны следующие пакеты:

• MiniSom — это инструмент на основе NumPy для создания и обучения SOM.
• NumPy используется для доступа к математическим функциям, таким как разделение массивов, получение уникальных значений и т.д.
• matplotlib используется для построения различных графиков и диаграмм для визуализации данных.
• Пакет datasets из sklearn используется для импорта наборов данных, к которым будет применяться SOM. 
• Пакет MinMaxScaler из sklearn нормализует набор данных. 

Следующий фрагмент кода импортирует эти пакеты: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

Подготовка набора данных

В этом учебном пособии мы используем MiniSom для построения SOM, а затем обучаем его на каноническом наборе данных IRIS. Этот набор данных состоит из 3 классов ирисов. Каждый класс содержит 50 экземпляров. Чтобы подготовить данные, мы выполняем следующие шаги: 

• Импортируем набор данных Iris из sklearn, 
• Извлекаем векторы данных и целевые скаляры. 
• Нормализуйте векторы данных. В этом руководстве мы используем MinMaxScaler из scikit-learn.
• Объявите набор меток для каждого из трех классов растений Ирис.

Следующий код реализует эти шаги:

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

Реализация самоорганизующихся карт (SOM) на Python

Чтобы реализовать SOM на Python, мы определяем и инициализируем сетку перед обучением ее на наборе данных. Затем мы можем визуализировать обученные нейроны и сгруппированный набор данных.

Определение сетки SOM

Как уже объяснялось ранее, SOM представляет собой сетку нейронов. С помощью MiniSom мы можем создать двумерные сетки. Размеры сетки по осям X и Y определяются количеством нейронов вдоль каждой оси. Чтобы определить сетку SOM, нам также нужно указать:

• Размеры сетки по осям X и Y
• Количество входных переменных – это количество строк данных.

Объявите эти параметры как константы Python:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

Пример кода ниже иллюстрирует, как объявить сетку с использованием MiniSom:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

Первые два параметра – это количество нейронов вдоль осей X и Y, а третий параметр – это количество переменных.

Мы объявляем другие параметры и гиперпараметры при создании сетки SOM. Мы объясним их позже в учебнике. Пока объявите эти параметры, как показано ниже:

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

Создайте SOM, используя эти параметры:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

Инициализация нейронов

Вышеуказанная команда создает SOM со случайными весами для всех нейронов. Инициализация нейронов с весами, взятыми из данных (вместо случайных чисел), может сделать процесс обучения более эффективным.

При использовании MiniSom для создания самоорганизующейся карты (SOM) есть два способа инициализации весов нейронов на основе данных:

• Случайная инициализация: Начальные веса нейронов случайным образом выбираются из входных данных. Мы делаем это, применяя функцию .random_weights_init() к СОМ. 
• Инициализация PCA: Инициализация с помощью метода главных компонент (PCA) использует главные компоненты входных данных для инициализации весов. Начальные веса нейронов охватывают первые две главные компоненты. Это часто приводит к более быстрой сходимости.

В этом руководстве мы используем инициализацию PCA. Чтобы применить инициализацию PCA к весам SOM, используйте функцию .pca_weights_init() как показано ниже:

som.pca_weights_init(data)

Обучение SOM

Процесс обучения обновляет веса SOM, чтобы минимизировать расстояние между нейронами и точками данных.

Ниже мы объясняем итеративный процесс обучения:

• Инициализация: Векторы весов всех нейронов инициализируются, как правило, случайными значениями. Также возможно инициализировать веса, выбирая из распределения входных данных.
• Выбор входных данных: Входной вектор (случайным образом) выбирается из обучающего набора данных.
• Идентификация BMU: Нейрон с вектором весов, наиболее близким к входному вектору, идентифицируется как BMU.
• Обновление соседей: BMU и его соседние нейроны обновляют свои векторные весы. Скорость обучения и функция соседства определяют, какие нейроны обновляются и на сколько. На шаге итерации t, учитывая входной вектор x, вектор весов нейрона i равен w_i, скорость обучения (t), и функция соседства h_bi (эта функция количественно оценивает степень обновления для нейрона i с учетом нейрона BMU b), формула обновления веса для нейрона i выражается как:
• Скорость уменьшения скорости обучения и радиуса соседства: Как скорость обучения, так и радиус соседства уменьшаются со временем. На более ранних итерациях процесс обучения вносит большие изменения в более широком окружении. Поздние итерации помогают уточнить веса, внося меньшие изменения в веса соседних нейронов. Это позволяет карте стабилизироваться и сходиться.

Чтобы обучить SOM, мы представляем модели входные данные. Мы можем выбрать один из двух подходов для этого:

• Выбирать образцы случайным образом из входных данных. Функция .train_random() реализует эту технику.
• Последовательно обрабатывать векторы во входных данных. Это делается с помощью функции .train_batch() функция.

Эти функции принимают входные данные и количество итераций в качестве параметров. В этом руководстве мы используем функцию .train_random() функция. Объявите количество итераций как константу и передайте его в функцию обучения:

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

После выполнения скрипта и завершения обучения отображается сообщение с ошибкой квантизации:

quantization error: 0.05357240680504421 

Ошибка квантования указывает на количество информации, потерянной при квантовании (уменьшении размерности) данных в SOM. Большая ошибка квантования указывает на большее расстояние между нейронами и точками данных. Это также означает, что кластеризация менее надежна.

Визуализация нейронов SOM

Теперь у нас есть обученная модель SOM. Чтобы визуализировать ее, мы используем карту расстояний (также известную как U-матрица). Карта расстояний отображает нейроны SOM в виде сетки ячеек. Цвет каждой ячейки представляет собой расстояние до соседних нейронов.

Карта расстояний представляет собой сетку с такими же размерами, как и SOM. Каждая ячейка на карте расстояний является нормализованной суммой (евклидовых) расстояний между нейроном и его соседями.

Получите доступ к карте расстояний SOM с помощью функции .distance_map(). Чтобы сгенерировать U-матрицу, следуем этим шагам:

• Используйте pyplot для создания фигуры с теми же размерами, что и SOM. В этом примере размеры составляют 8×8.
• Постройте карту расстояний, используя matplotlib и функцию .pcolor() . В этом примере мы используем gist_yarg в качестве цветовой схемы.
• Отобразите colorbar, индекс, сопоставляющий различные цвета с различными скалярными значениями. В данном случае, поскольку расстояния нормализованы, скалярные значения расстояний варьируются от 0 до 1.

Код ниже реализует эти шаги:

# создайте сетку
plt.figure(figsize=(8, 8))
# постройте карту расстояний
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# покажите цветовую шкалу
plt.colorbar()
plt.show()

В этом примере U-матрица использует монотонную цветовую схему. Это можно понять, следуя этим рекомендациям:

• Светлые оттенки представляют нейроны, расположенные близко друг к другу, а темные оттенки обозначают нейроны, находящиеся дальше от других.
• Группы более светлых оттенков могут быть интерпретированы как кластеры. Темные узлы между кластерами могут быть интерпретированы как границы между кластерами.

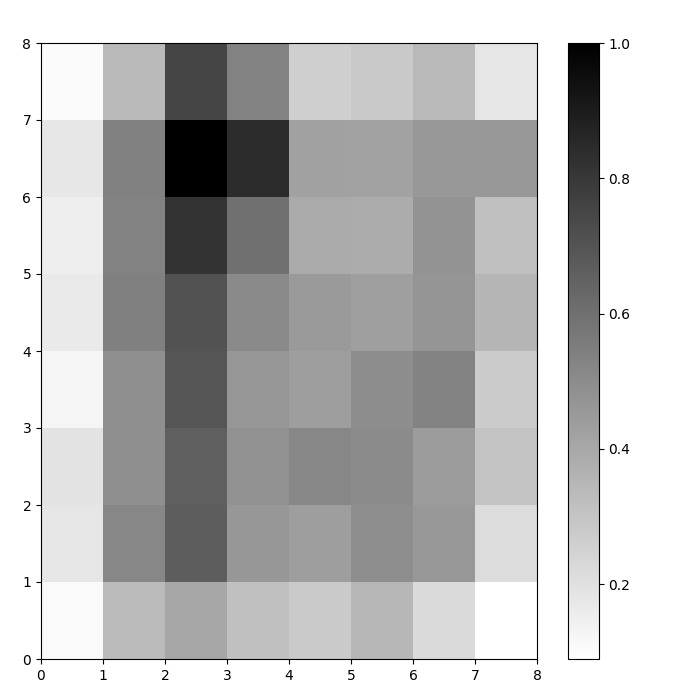
Рисунок 1: U-матрица SOM, обученная на наборе данных Iris (изображение автора)

Оценка результатов кластеризации SOM

Предыдущий рисунок графически иллюстрировал нейроны SOM. В этом разделе мы покажем, как визуализировать, как SOM кластеризовал данные.

Идентификация кластеров

Мы накладываем маркеры на вышеуказанную U-матрицу, чтобы обозначить, какой класс растения Iris представляет каждая ячейка (нейрон). Для этого:

• Как и раньше, создайте фигуру 8×8 с использованием pyplot, постройте карту расстояний и отобразите цветовую шкалу. 
• Укажите массив из трех маркерoв matplotlib, по одному для каждого класса растения Iris. 
• Укажите массив из трех цветовых кодов matplotlib, по одному для каждого класса растения Iris. 
• Итеративно изображайте выигравший нейрон для каждой точки данных:
• Определите (координаты) выигравшего нейрона для каждой точки данных, используя функцию .winner(). 
• Постройте положение каждого выигравшего нейрона в центре каждой ячейки на сетке. w[0] и w[1] дают X и Y координаты нейрона соответственно. К каждой координате добавляется значение 0.5, чтобы отобразить его в центре ячейки. 

Ниже приведён код, который показывает, как это сделать:

# постройте карту расстояний
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# создайте маркеры и цвета для каждого класса
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# постройте выигравший нейрон для каждой точки данных
for count, datapoint in enumerate(data):
    # получите победителя
    w = som.winner(datapoint)  
    # разместите маркер на выигрышной позиции для образца точки данных
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

Полученное изображение показано ниже:

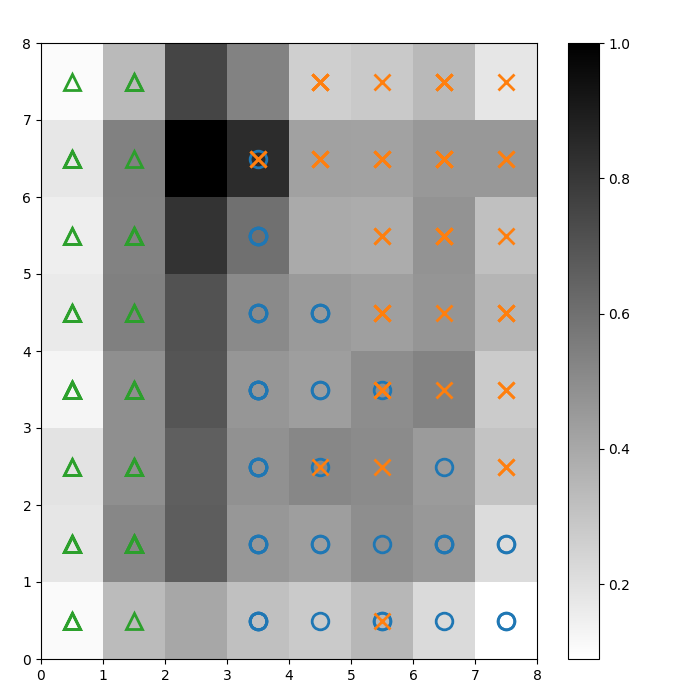
Рисунок 2: U-матрица с наложенными маркерами классов (изображение автора)

Основываясь на документации датасета Iris, “один класс линейно отделим от других 2; последние не являются линейно отделимыми друг от друга”. В U-матрице выше эти три класса представлены тремя маркерами – треугольником, кругом и крестом. 

Обратите внимание, что между синими кругами и оранжевыми крестами нет четкой границы. Кроме того, два класса накладываются на один и тот же нейрон во многих ячейках. Это означает, что нейрон находится на равном расстоянии от обоих классов. 

Визуализация результата кластеризации

СОМ — это модель кластеризации. Похожие данные сопоставляются с одним и тем же нейроном. Данные одной и той же категории сопоставляются с кластером соседних нейронов. Мы отображаем все данные на сетке СОМ, чтобы лучше изучить поведение кластеризации.

Следующие шаги описывают, как создать этот разбросанный график:

• Получите X и Y координаты выигравшего нейрона для каждой точки данных.
• Постройте карту расстояний, как мы сделали для Рисунок 1.
• Используйте plt.scatter(), чтобы построить точечную диаграмму всех выигравших нейронов для каждой точки данных. Добавьте случайное смещение к каждой точке, чтобы избежать перекрытия между точками данных в одной ячейке.

Мы реализуем эти шаги в коде ниже:

# получаем X и Y координаты выигравшего нейрона для каждой точки данныхw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# строим карту расстояний
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# создаем точечную диаграмму всех выигравших нейронов для каждой точки данных
# добавляем случайное смещение к каждой точке, чтобы избежать перекрытий
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

Следующий график показывает результирующую точечную диаграмму:

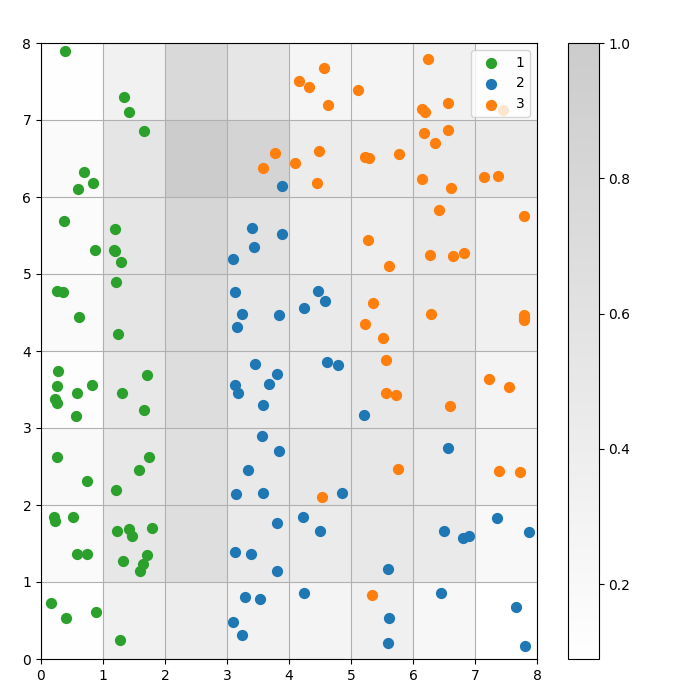Рисунок 3: Диаграмма рассеяния точек данных в ячейках (изображение автора)

На вышеуказанной диаграмме рассеяния обратите внимание на: 

• Некоторые ячейки содержат как синие, так и оранжевые точки. 
• Зеленые точки явно отделены от остальных данных, но синие и оранжевые точки не отделены четко. 
• Вышеуказанные наблюдения соответствуют тому факту, что только один из трех кластеров в наборе данных Iris имеет четкую границу.
• В Рисунке 1, темные узлы между кластерами (которые можно интерпретировать как границы между кластерами) совпадают с пустыми ячейками на диаграмме рассеяния.

Вы можете получить доступ и запустить полный код в этом блокноте DataLab.

Настройка модели SOM

В предыдущих разделах показано, как создать и обучить модель SOM, а также как визуально изучить результаты. В этом разделе мы обсуждаем, как настроить производительность моделей SOM.

Ключевые гиперпараметры для настройки

Как и в случае с любой моделью машинного обучения, гиперпараметры значительно влияют на производительность модели.

Некоторые из гиперпараметров, важных для обучения SOM, включают:

• Размер сетки определяет размер карты. Количество нейронов на карте с размером сетки AxB составляет A*B.
• Скорость обучения определяет, насколько изменяются веса на каждой итерации. Мы устанавливаем начальную скорость обучения, и она уменьшается со временем в соответствии с функцией убывания.
• Функция убывания определяет степень, на которую скорость обучения уменьшается на каждой последующей итерации.
• Функциясоседства — это математическая функция, которая определяет, какие нейроны будут считаться соседями БМУ.
• Стандартноеотклонение определяет разброс функции соседства. Например, гауссовская функция соседства с высоким стандартным отклонением будет иметь большее соседство, чем та же функция с меньшим стандартным отклонением. Мы устанавливаем начальное стандартное отклонение, которое уменьшается со временем в соответствии с функцией затухания сигмы.
• Функция сигма-распад контролирует, насколько стандартное отклонение уменьшается на каждой последующей итерации. 
• Количество итераций обучения определяет, сколько раз обновляются веса. На каждой итерации обучения веса нейронов обновляются один раз. 
• Функция расстояния — это математическая функция, которая вычисляет расстояние между нейронами и данными.
• Топология определяет структуру сетки. Нейроны в сетке могут быть расположены в прямоугольном или шестиугольном паттерне.

В следующем разделе мы обсудим рекомендации по установке значений этих гиперпараметров.

Влияние настройки гиперпараметров

Значения гиперпараметров должны определяться на основе модели и набора данных. В какой-то степени определение этих значений является процессом проб и ошибок. В этом разделе мы даем рекомендации по настройке каждого гиперпараметра. Рядом с каждым гиперпараметром мы указываем (в скобках) соответствующие константы Python, используемые в примере кода.

• Размер сетки (SOM_X_AXIS_NODES и SOM_X_AXIS_NODES): Размер сетки зависит от размера набора данных. Правило заключается в том, что для набора данных размером N, сетка должна содержать примерно 5*sqrt(N) нейронов. Например, если набор данных содержит 150 образцов, сетка должна содержать 5*sqrt(150) = примерно 61 нейрон. В этом учебном пособии набор данных Iris содержит 150 строк, и мы используем сетку 8×8. 
• Начальная скорость обучения (ALPHA): Более высокая скорость ускоряет сходимость, в то время как более низкие скорости используются для более тонкой настройки после ранних итераций. Начальная скорость обучения должна быть достаточно большой, чтобы обеспечить быструю адаптацию, но не настолько большой, чтобы превышать оптимальные значения весов. В этой статье начальная скорость обучения составляет 0.5. 
• Начальное стандартное отклонение (SIGMA0): Оно определяет начальный размер или разброс окрестности. Более крупное значение учитывает более глобальные паттерны. В этом примере мы используем начальное стандартное отклонение 1.5. 
• Для коэффициента распада (DECAY_FUNC) и коэффициента сигма распада (SIGMA_DECAY_FUNC), мы можем выбрать один из трех типов функций распада: 
• Обратное затухание: Эта функция подходит, если данные имеют как глобальные, так и локальные паттерны. В таких случаях нам нужна более длительная фаза широкого обучения, прежде чем сосредоточиться на локальных паттернах.
• Линейное затухание: Это хорошо подходит для наборов данных, где мы хотим стабильный и равномерный размер соседства или снижение скорости обучения. Это полезно, если данным не нужно много тонкой настройки.
• Ассимптотическое затухание: Эта функция полезна, если данные сложные и многомерные. В таких случаях лучше потратить больше времени на глобальное исследование, прежде чем постепенно переходить к более тонким деталям.
• Функция соседства (NEIGHBORHOOD_FUNC): По умолчанию используется функция Гаусса. Также применяются другие функции, как объяснено ниже. 
• Гауссова (по умолчанию): Это кривая в форме колокола. Степень обновления нейрона плавно уменьшается по мере увеличения расстояния от выигравшего нейрона. Она обеспечивает плавный и непрерывный переход и сохраняет топологию данных. Подходит для большинства общих целей благодаря своей стабильной и предсказуемой работе.
• Пузыри: Эта функция создает фиксированное по ширине соседство. Все нейроны внутри этого соседства обновляются одинаково, а нейроны за его пределами не обновляются (для данной точки данных). Это вычислительно дешевле и проще в реализации. Это полезно для маленьких карт, где резкие границы соседства не компрометируют эффективную кластеризацию. 
• Мексиканская шляпа: У нее есть центральная положительная область, окруженная отрицательной областью. Нейроны, близкие к BMU, обновляются, чтобы приблизиться к точке данных, а нейроны, находящиеся дальше, обновляются, чтобы удалиться от точки данных. Эта техника усиливает контраст и уточняет характеристики на карте. Так как она подчеркивает отдельные кластеры, она эффективна в задачах распознавания образов, где требуется четкое разделение кластеров.
• Треугольник: Эта функция определяет размер окрестности как треугольник, при этом BMU имеет наибольшее влияние. Он уменьшается линейно с расстоянием от BMU. Используется для кластеризации данных с постепенными переходами между кластерами или признаками, такими как изображения, речь или временные ряды, где соседние точки данных ожидаются как имеющие схожие характеристики.
• Функция расстояния (DISTANCE_FUNC): Для измерения расстояния между нейронами и точками данных мы можем выбрать из 4 методов:
• Евклидово расстояние (выбор по умолчанию): Полезно, когда данные непрерывные, и мы хотим измерить расстояние по прямой. Оно подходит для большинства общих задач, особенно когда точки данных равномерно распределены и пространственно связаны.
• Косинусное расстояние: Хороший выбор для текста или разреженных данных высокой размерности, где угол между векторами более важен, чем величина. Оно полезно для сравнения направленности в данных.
• Манхэттенское расстояние: Идеально подходит, когда точки данных находятся на сетке или решетке (например, городские кварталы). Оно менее чувствительно к выбросам, чем Евклидово расстояние.
• Расстояние Чебышева: Подходит для ситуаций, когда движение может происходить в любом направлении (например, расстояния на шахматной доске). Полезно для дискретных пространств, где мы хотим приоритизировать максимальное различие по осям.
• Топология (TOPOLOGY): В сетке нейроны могут быть расположены в гексагональной или прямоугольной структуре: 
• Прямоугольный (по умолчанию): каждый нейрон имеет 4 непосредственных соседа. Это правильный выбор, когда данные не имеют четкой пространственной связи. Это также вычислительно проще.
• Шестиугольный: каждый нейрон имеет 6 соседей. Это предпочитаемый вариант, если данные имеют пространственные связи, которые лучше представлены с помощью шестиугольной сетки. Это относится к круговым или угловым распределениям данных.
• Количество итераций обучения (N_ITERATIONS): В принципе, более длительное время обучения приводит к снижению ошибок и лучшему соответствию весов входным данным. Однако производительность модели увеличивается асимптотически с количеством итераций. Таким образом, после определенного количества итераций увеличение производительности от последующих взаимодействий становится лишь незначительным. Определение правильного количества итераций требует некоторого эксперимента. В этом уроке мы обучаем модель в течение 5000 итераций. 

Чтобы определить правильную конфигурацию гиперпараметров, мы рекомендуем экспериментировать с различными вариантами на меньшем подмножестве данных.

Заключение

Самоорганизующиеся карты являются надежным инструментом для обучения без учителя. Они используются для кластеризации, уменьшения размерности, обнаружения аномалий и визуализации данных. Поскольку они сохраняют топологические свойства многомерных данных и представляют их на сетке с меньшей размерностью, SOM облегчают визуализацию и интерпретацию сложных наборов данных.

В этом уроке обсуждаются основные принципы SOM и показывается, как реализовать SOM с использованием библиотеки MiniSom на Python. Также демонстрируется, как визуально проанализировать результаты и объясняются важные гиперпараметры, используемые для обучения SOM и настройки их производительности.