介紹
多元線性回歸是一種基本的統計技術,用於模擬因變量與多個自變量之間的關係。在Python中,像scikit-learn和statsmodels這樣的工具提供了強大的回歸分析實現。本教程將指導您使用Python實珽、解釋和評估多元線性回歸模型。
先決條件
在開始實珽之前,請確保您具備以下條件:
- 基本的Python理解。您可以參考Python入門教程。
- 熟悉scikit-learn用於機器學習任務。您可以參考Python scikit-learn教程。
- 在 Python 中理解数据可视化概念。您可以参考使用 matplotlib 在 Python 3 中绘制数据和在 Python 3 中使用 pandas 和 Jupyter Notebook 进行数据分析和可视化。
- 已安装 Python 3.x,并安装了以下库:
numpy、pandas、matplotlib、seaborn、scikit-learn和statsmodels。
什么是多元线性回归?
多元线性回归(MLR)是一种统计方法,用于建模因变量与两个或更多自变量之间的关系。它是简单线性回归的扩展,简单线性回归是用于建模因变量与单个自变量之间的关系。在 MLR 中,关系使用以下公式建模:
.png)
其中:
.png)
例如:根据房屋的大小、卧室数量和位置来预测房屋的价格。在这种情况下,有三个自变量,即大小、卧室数量和位置,和一个因变量,即价格,需要预测的值。
多重線性回歸的假設
在執行多重線性回歸之前,必須確保滿足以下假設:
-
線性: 因變量和自變量之間的關係是線性的。
-
誤差獨立性: 殘差(誤差)彼此獨立。這通常通過 杜賓-沃森檢定 來驗證。
-
同方差性: 殘差的方差在所有自變量的水平上都是常數。殘差圖可以幫助驗證這一點。
-
無多重共線性:獨立變數之間沒有高度相關。通常使用變異膨脹因子(VIF)來檢測多重共線性。
-
殘差的正態性:殘差應該符合正態分佈。可以使用Q-Q 圖來檢查。
-
異常值影響:異常值或高杠杆點不應該對模型產生不成比例的影響。
這些假設確保迴歸模型是有效的,結果是可靠的。未能滿足這些假設可能導致結果出現偏誤或具有誤導性。
預處理資料
在這個部分,您將學習如何在Python中使用多元線性回歸模型,根據加州房屋數據集的特徵來預測房屋價格。您將學會如何預處理資料、擬合回歸模型,並評估其性能,同時解決常見的問題,如多重共線性、離群值和特徵選擇。
步驟1 – 載入數據集
您將使用加州房屋數據集,這是一個流行的回歸任務數據集。該數據集包含有關波士頓郊區房屋的13個特徵,以及它們對應的房屋中位價格。
首先,讓我們安裝必要的套件:
您應該觀察到數據集的以下輸出:
以下是每個屬性的含義:
| Variable | Description |
|---|---|
| MedInc | 區塊內的收入中位數 |
| HouseAge | 區塊內的房屋年齡中位數 |
| AveRooms | 平均房間數 |
| AveBedrms | 平均臥室數 |
| Population | 區塊人口數 |
| AveOccup | 平均房屋佔用率 |
| Latitude | 房屋區塊緯度 |
| Longitude | 房屋區塊經度 |
步驟 2 – 數據預處理
檢查遺失值
確保數據集中沒有遺失值,這可能會影響分析結果。
輸出:
特徵選擇
首先讓我們創建一個相關矩陣,以了解變量之間的依賴關係。
輸出:
您可以分析上述相關矩陣,以選擇我們回歸模型中的依賴變量和獨立變量。相關矩陣提供了數據集中每對變量之間關係的見解。
在給定的相關矩陣中,MedHouseValue 是依賴變量,因為它是我們試圖預測的變量。獨立變量與 MedHouseValue 之間具有顯著的相關性。
根據相關矩陣,您可以識別以下與 MedHouseValue 具有顯著相關性的獨立變量:
MedInc:此變量與MedHouseValue之間有強正相關(0.688075),表明隨著中位收入的增加,中位房價也傾向於上升。AveRooms:此變量與MedHouseValue之間有中等正相關(0.151948),表明隨著每戶平均房間數的增加,中位房價也傾向於上升。AveOccup:此變數與MedHouseValue之間有弱負相關性(-0.023737),表示隨著每戶的平均佔用率增加,房屋中位數價值傾向於下降,但這種影響相對較小。
通過選擇這些獨立變數,您可以建立一個回歸模型,以捕捉這些變數與MedHouseValue之間的關係,從而根據中位數收入、平均房間數和平均佔用率對中位數房屋價值進行預測。
您也可以使用以下代碼在Python中繪製相關矩陣:
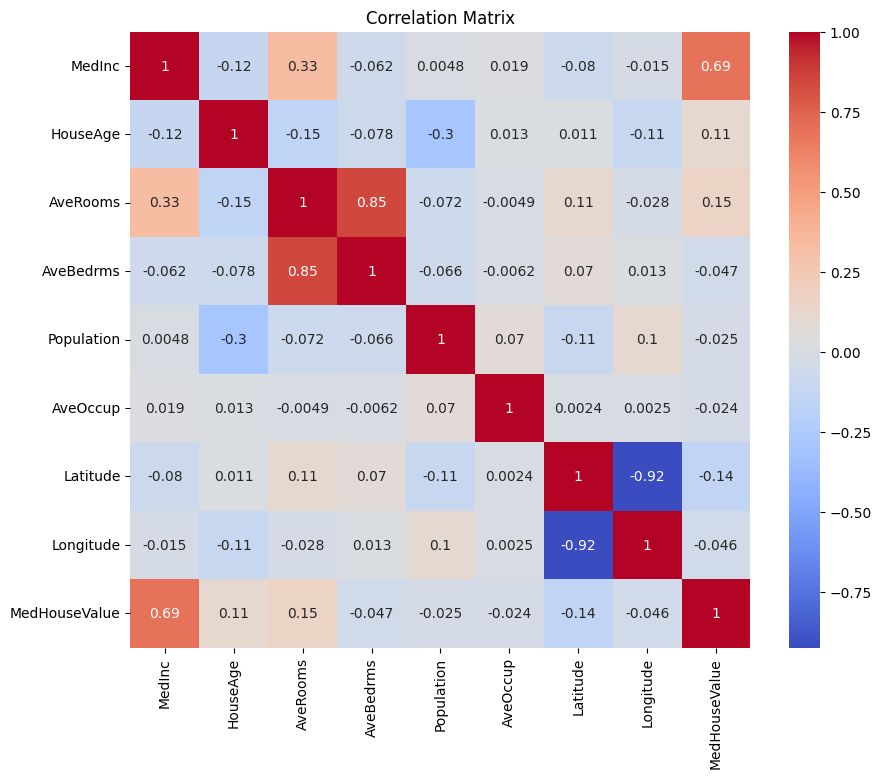
基於上述內容,您將專注於幾個關鍵特徵以簡化分析,例如MedInc(中位數收入)、AveRooms(每戶平均房間數)和AveOccup(每戶平均佔用率)。
上述代碼區塊從housing_df數據框中選擇特定特徵進行分析。所選特徵為MedInc、AveRooms和AveOccup,這些特徵存儲在selected_features列表中。
然後,housing_df的DataFrame被子集化,只包括這些選定的特徵,結果存儲在X列表中。
目標變數MedHouseValue從housing_df中提取並存儲在y列表中。
特徵縮放
您將使用標準化來確保所有特徵處於相同的尺度上,從而提高模型性能和可比較性。
標準化是一種預處理技術,將數值特徵縮放為均值為0,標準差為1。這個過程確保所有特徵處於相同的尺度上,對於機器學習模型對輸入特徵尺度敏感的情況至關重要。通過對特徵進行標準化,可以通過減少具有大範圍的特徵影響模型,從而提高模型性能和可比較性。
輸出:
該輸出表示應用StandardScaler後特徵MedInc、AveRooms和AveOccup的縮放值。這些值現在以0為中心,標準差為1,確保所有特徵處於相同的尺度上。
第一行[ 2.34476576 0.62855945 -0.04959654]表示對於第一個數據點,縮放後的MedInc值為2.34476576,AveRooms為0.62855945,AveOccup為-0.04959654。同樣,第二行[ 2.33223796 0.32704136 -0.09251223]表示第二個數據點的縮放值,依此類推。
縮放值範圍約為 -1.14259331 到 2.34476576,這表示特徵已經被正規化並且具有可比性。這對於對輸入特徵的尺度敏感的機器學習模型至關重要,因為這可以防止具有大範圍的特徵主導模型。
實現多元線性回歸
現在您已經完成了數據預處理,讓我們在 Python 中實現多元線性回歸。
train_test_split 函數用於將數據分為訓練集和測試集。在這裡,80% 的數據用於訓練,20% 用於測試。
該模型使用均方誤差和 R 平方來評估。均方誤差 (MSE) 測量的是誤差或偏差的平方的平均值。
R 平方 (R2) 是一種統計測量,表示在回歸模型中由自變量解釋的因變量方差的比例。
輸出:
上面的輸出提供了兩個關鍵指標來評估多元線性回歸模型的性能:
均方誤差 (MSE): 0.7006855912225249
MSE 測量預測值與目標變數的實際值之間的平均平方差。較低的 MSE 表示模型表現更好,因為這意味著模型的預測更準確。在這個案例中,MSE 為 0.7006855912225249,表明模型不是完美的,但具有合理的準確性。MSE 的值通常應該接近 0,較低的值表示更好的表現。
決定係數 (R2): 0.4652924370503557
決定係數 測量因變數中可以從自變數中預測的變異比例。其範圍從 0 到 1,其中 1 表示完美預測,0 表示沒有線性關係。在這個案例中,R2 值為 0.4652924370503557,表明約 46.53% 的目標變數的變異可以由模型中使用的自變數來解釋。這表明模型能夠捕捉到變數之間的重要關係,但並非所有關係。
讓我們來看看一些重要的圖表:

.png)
使用 statsmodels
在 Python 中的 Statsmodels 函式庫是一個強大的統計分析工具。它提供了多種統計模型和檢驗,包括線性回歸、時間序列分析和非參數方法。
在多重線性回歸的背景下,statsmodels 可用於將線性模型擬合到數據中,然後對該模型進行各種統計檢驗和分析。這對於了解自變量和因變量之間的關係,以及基於模型進行預測特別有用。
輸出:
這是上述表格的摘要:
模型摘要
該模型是一個普通最小二乘回歸模型,屬於線性回歸模型的一種。因變量是MedHouseValue,模型的R平方值為0.485,這表示大約48.5%的MedHouseValue變異可以由自變量解釋。調整後的R平方值為0.484,這是R平方的一個修正版本,對於包含額外自變量的模型進行懲罰。
模型擬合
該模型是使用最小二乘法擬合的,F統計量為5173,這表明模型擬合良好。在假設虛無假設為真的情況下,觀察到至少與觀察到的F統計量同樣極端的F統計量的概率大約為0。這表明該模型在統計上是顯著的。
模型係數
模型係數如下:
- 常數項為2.0679,這表明當所有自變量為0時,預測的
MedHouseValue約為2.0679。 - 自變量
x1(在這種情況下為MedInc)的係數為0.8300,這表示每增加一個單位的MedInc,預測的MedHouseValue約增加0.83個單位,假設所有其他自變量保持不變。 - 在這種情況下,
x2(即AveRooms)的係數為-0.1000,這表示對於x2每增加一個單位,預測的MedHouseValue將減少約0.10個單位,假設所有其他自變量保持不變。 x3(即AveOccup)的係數為-0.0397,這表示對於x3每增加一個單位,預測的MedHouseValue將減少約0.04個單位,假設所有其他自變量保持不變。
模型診斷
模型診斷如下:
- Omnibus檢定統計量為3981.290,這表示殘差不服從正態分佈。
- Durbin-Watson統計量為1.983,這表示殘差中沒有顯著的自相關性。
- Jarque-Bera檢定統計量為11583.284,這表示殘差不服從正態分佈。
- 殘差的偏度為1.260,這表示殘差呈右偏。
- 殘差的峰態為6.239,這表示殘差呈leptokurtic(即比正態分佈有更高的峰值和更重的尾部)。
- 條件數為1.42,這表示模型對數據的微小變化不敏感。
.png)
處理多重共線性
多重共線性是在多元線性迴歸中常見的問題,當兩個或更多獨立變數彼此高度相關時,會導致係數的估計不穩定且不可靠。
為了檢測和處理多重共線性,您可以使用方差膨脹因子。VIF測量如果您的預測變數相關,估計的迴歸係數的方差會增加多少。一個VIF值為1意味著給定的預測變數與其他預測變數之間沒有相關性。超過5或10的VIF值表示存在問題的共線性量。
在下面的代碼塊中,讓我們計算模型中每個獨立變數的VIF。如果任何VIF值超過5,您應考慮從模型中移除該變數。
輸出:
每個特徵的VIF值如下:
MedInc:VIF值為1.120166,表明與其他獨立變數的相關性非常低。這表明MedInc與模型中的其他獨立變數不高度相關。AveRooms:VIF值為1.119797,表明與其他獨立變數的相關性非常低。這表明AveRooms與模型中的其他獨立變數不高度相關。AveOccup:VIF 值為 1.000488,表示與其他自變量之間沒有相關性。這表明AveOccup與模型中的其他自變量無關聯。
一般來說,這些 VIF 值均低於 5,表明模型中的自變量之間沒有顯著的多重共線性。這顯示模型穩定可靠,自變量的係數不會受到多重共線性的顯著影響。
.png)
交叉驗證技術
交叉驗證是一種用於評估機器學習模型性能的技術。這是一種重抽樣程序,用於在數據樣本有限的情況下評估模型。該程序有一個名為 k 的參數,表示將給定數據樣本分為的組數。因此,該程序通常稱為 k 倍交叉驗證。
輸出:
交叉驗證得分顯示模型在未見數據上的表現。得分範圍從 0.31191043 到 0.51269138,表明模型在不同折數中的表現有所變化。得分越高,表現越好。
平均 CV R^2 分數為 0.41864482644003276,這表示模型平均解釋目標變數變異的約 41.86%。這是一個中等程度的解釋,表明模型在預測目標變數方面有一定效果,但可能需要進一步改進或精煉。
這些分數可用於評估模型的泛化能力並找出潛在的改進領域。
.png)
特徵選擇方法
遞歸特徵消除 方法是一種特徵選擇技術,它會遞歸性地消除最不重要的特徵,直到達到指定的特徵數。該方法在處理大量特徵且目標是選擇最具信息量特徵的子集時尤其有用。
在提供的程式碼中,首先從 sklearn.feature_selection 導入 RFE 類。然後創建一個具有指定估計器(在本例中為 LinearRegression)的 RFE 實例,並將 n_features_to_select 設置為 2,表示我們要選擇前 2 個特徵。
接下來,我們將 RFE 物件擬合到我們的標準化特徵 X_scaled 和目標變數 y。RFE 物件的 support_ 屬性返回一個布林掩碼,指示哪些特徵被選中。
為了可視化特徵的排名,您可以創建一個包含特徵名稱及其相應排名的 DataFrame。RFE 物件的 ranking_ 屬性返回每個特徵的排名,較低的值表示更重要的特徵。然後,您可以繪製特徵排名的條形圖,按排名值排序。這個圖有助於我們理解每個特徵在模型中的相對重要性。
輸出:
.png)
根據上述圖表,最合適的兩個特徵是 MedInc 和 AveRooms。這也可以通過上面的模型輸出來驗證,因為因變數 MedHouseValue 主要依賴於 MedInc 和 AveRooms。
常見問題
如何在 Python 中實現多元線性回歸?
要在Python中實現多元線性回歸,您可以使用像statsmodels或scikit-learn之類的庫。這裡是使用scikit-learn的快速概述:
這演示了如何擬合模型、獲取係數並進行預測。
多元線性回歸在Python中的假設是什麼?
多元線性回歸依賴於幾個假設來確保有效結果:
- 線性:預測變數與目標變量之間的關係是線性的。
- 獨立性:觀察結果彼此獨立。
- 同方差性:殘差(誤差)的方差在所有自變量的水平上是恆定的。
- 殘差的正態性:殘差呈正態分佈。
- 無多重共線性:自變量之間不高度相關。
您可以使用殘差圖、方差膨脹因子 (VIF) 或統計檢驗等工具來測試這些假設。
如何在 Python 中解釋多元回歸結果?
回歸結果的關鍵指標包括:
- 係數 (coef_):表示在其他變量保持不變的情況下,目標變量對應預測變量單位變化的變化量。
示例:X1 的係數為 2,意味著當 X1 增加 1 單位時,目標變量增加 2,保持其他變量不變。
2.截距 (intercept_):代表當所有預測變量為零時目標變量的預測值。
3.R 平方:解釋預測變量解釋的目標變量變異的比例。
示例:R^2 為 0.85 表示模型解釋了目標變量 85% 的變異性。
4.P 值(在 statsmodels 中):評估預測變量的統計顯著性。P 值 < 0.05 通常表示預測變量是顯著的。
簡單線性回歸和多重線性回歸在Python中的區別是什麼?
| Feature | Simple Linear Regression | Multiple Linear Regression |
|---|---|---|
| 獨立變量的數量 | 一個 | 多於一個 |
| 模型方程 | y = β0 + β1x + ε | y = β0 + β1×1 + β2×2 + … + βnxn + ε |
| 假設 | 與多重線性回歸相同,但只有一個獨立變量 | 與簡單線性回歸相同,但有額外的假設以適用於多個獨立變量 |
| 係數解釋 | 在保持所有其他變量不變的情況下,目標變量對於獨立變量單位變化的變化(不適用於簡單線性回歸) | 在保持所有其他獨立變量不變的情況下,目標變量對於一個獨立變量單位變化的變化 |
| 模型複雜性 | 較少複雜 | 較複雜 |
| 模型靈活性 | 較不靈活 | 較靈活 |
| 過擬合風險 | 較低 | 較高 |
| 可解釋性 | 更易於解釋 | 更具挑戰性的解釋 |
| 適用性 | 適用於簡單關係 | 適用於多因素的複雜關係 |
| 範例 | 根據臥室數量預測房價 | 根據臥室數量、平方英尺和地點預測房價 |
結論
在這個綜合教程中,您學會了如何使用加州住房數據集實施多元線性回歸。您處理了多重共線性、交叉驗證、特徵選擇和正則化等關鍵方面,為每個概念提供了徹底的理解。您還學會了如何整合視覺化來說明殘差、特徵重要性和整體模型性能。您現在可以輕鬆地在Python中構建穩健的回歸模型,並將這些技能應用於現實世界的問題。
Source:
https://www.digitalocean.com/community/tutorials/multiple-linear-regression-python













