導入
複数の独立変数と1つの従属変数の間の関係をモデル化するために使用される基本的な統計的手法である多重線形回帰。Pythonでは、scikit-learnやstatsmodelsなどのツールが回帰分析の堅牢な実装を提供しています。このチュートリアルでは、Pythonを使用して複数の線形回帰モデルを実装、解釈、評価する方法を説明します。
前提条件
実装に取り組む前に、以下の準備が整っていることを確認してください。
- Pythonの基本的な理解。初心者向けのPythonチュートリアルを参照してください。
- 機械学習タスクのためのscikit-learnの操作方法に精通していること。Python scikit-learnチュートリアルを参照してください。
- Pythonでのデータ可視化の概念の理解。 matplotlibを使用してPython 3でデータをプロットする方法およびPython 3でpandasとJupyter Notebookを使用したデータ分析と可視化を参照してください。
- Python 3.xが以下のライブラリ
numpy、pandas、matplotlib、seaborn、scikit-learn、およびstatsmodelsとともにインストールされています。
多重線形回帰とは?
多重線形回帰(MLR)は、従属変数と2つ以上の独立変数との関係をモデル化する統計的手法です。これは、単回帰分析の拡張であり、単一の独立変数との関係をモデル化します。MLRでは、関係は次の式を使用してモデル化されます:
.png)
ここで:
.png)
例:家の価格をサイズ、寝室数、場所に基づいて予測する。この場合、サイズ、寝室数、場所の3つの独立変数と価格の1つの従属変数(予測する値)があります。
多重線形回帰の仮定
多重線形回帰を実装する前に、以下の仮定が満たされていることを確認することが重要です。
-
線形性: 従属変数と独立変数との関係が線形であること。
-
誤差の独立性: 残差(誤差)が互いに独立していること。これは、Durbin-Watson検定を使用してしばしば確認されます。
-
均一分散性: 残差の分散が独立変数のすべてのレベルで一定であること。残差プロットを使用してこれを確認できます。
-
多重共線性がない:独立変数同士が高度に相関していない。多重共線性を検出するためには、分散膨張係数(VIF)が一般的に使用される。
-
残差の正規性:残差は正規分布に従うべきです。これはQ-Qプロットを使用して確認できます。
-
外れ値の影響:外れ値や高影響点がモデルに過度に影響を与えてはいけません。
これらの仮定は回帰モデルが妥当であり、結果が信頼できることを保証します。これらの仮定を満たさないと、バイアスのあるまたは誤解を招く結果につながる可能性があります。
データの前処理
このセクションでは、Pythonで複数の線形回帰モデルを使用して、California Housing Datasetからの特徴に基づいて家の価格を予測する方法を学びます。データの前処理方法、回帰モデルの適合、および多重共線性、外れ値、特徴選択などの一般的な課題に対処する方法を学びます。
ステップ1 – データセットの読み込み
回帰タスク向けの人気のあるデータセットであるCalifornia Housing Datasetを使用します。このデータセットには、ボストンの郊外の家に関する13の特徴とそれに対応する中央家価格が含まれています。
まず、必要なパッケージをインストールしましょう。
データセットの出力は以下のようになります:
各属性の意味は次の通りです:
| Variable | Description |
|---|---|
| MedInc | ブロック内の収入の中央値 |
| HouseAge | ブロック内の住宅の中央年齢 |
| AveRooms | 平均部屋数 |
| AveBedrms | 平均寝室数 |
| Population | ブロックの人口 |
| AveOccup | 平均住宅占有率 |
| Latitude | 住宅ブロックの緯度 |
| Longitude | 住宅ブロックの経度 |
ステップ2 – データの前処理
欠損値の確認
解析に影響を及ぼす可能性のあるデータセット内の欠損値がないことを確認します。
出力:
特徴選択
まず、相関行列を作成して変数間の依存関係を理解します。
出力:
上記の相関行列を分析して、回帰モデル用の依存変数と独立変数を選択できます。相関行列はデータセット内の各変数の関係に関する洞察を提供します。
与えられた相関行列では、MedHouseValueが予測しようとしている変数であるため、これが依存変数です。独立変数はMedHouseValueと有意な相関があります。
相関行列に基づいて、MedHouseValueと有意な相関がある次の独立変数を特定できます:
MedInc: この変数はMedHouseValueと強い正の相関(0.688075)を示し、収入が増加すると住宅価格も増加する傾向があることを示しています。AveRooms: この変数はMedHouseValueと中程度の正の相関(0.151948)を示し、世帯当たりの平均部屋数が増加すると住宅価格も増加する傾向があることを示しています。AveOccup: この変数は、MedHouseValueと弱い負の相関(-0.023737)を持ちます。これは、世帯当たりの平均占有率が増加すると、家の価値の中央値が低下する傾向があることを示していますが、その影響は比較的小さいです。
これらの独立変数を選択することで、MedHouseValue との間の関係を捉えた回帰モデルを構築することができます。これにより、収入中央値、平均部屋数、平均占有率に基づいて家の価値の中央値について予測を行うことができます。
以下を使用して、Python で相関行列をプロットすることもできます:
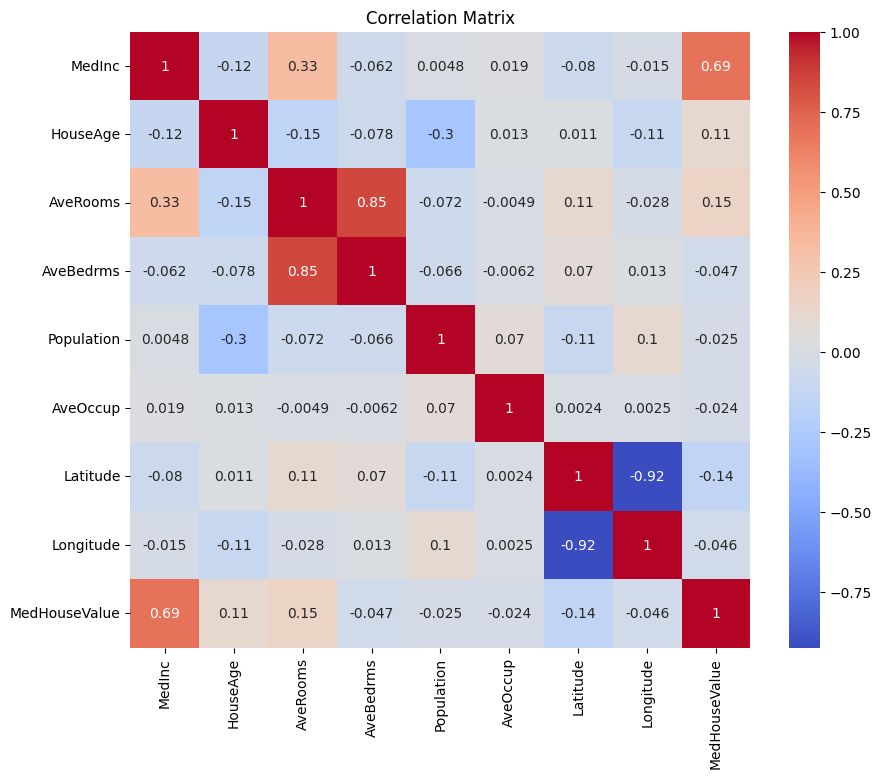
上記の内容に基づいて、MedInc(収入中央値)、AveRooms(世帯当たりの平均部屋数)、AveOccup(世帯当たりの平均占有率)など、いくつかの主要な特徴に焦点を当てることになります。
上記のコードブロックは、分析のために housing_df データフレームから特定の特徴を選択します。選択された特徴は、MedInc、AveRooms、AveOccupであり、これらは selected_features リストに格納されます。
データフレーム housing_df は、これらの選択された特徴のみを含むようにサブセット化され、その結果が X リストに格納されます。
目的変数 MedHouseValue は housing_df から抽出され、y リストに格納されます。
特徴のスケーリング
特徴量がすべて同じ尺度になるように標準化を使用し、モデルのパフォーマンスと比較性を向上させます。
標準化は、数値的な特徴量を平均が0、標準偏差が1になるようにスケーリングする前処理技術です。このプロセスにより、すべての特徴量が同じ尺度に揃い、入力特徴量の尺度に敏感な機械学習モデルにとって重要です。特徴量を標準化することで、大きな範囲を持つ特徴がモデルを支配する効果を軽減し、モデルのパフォーマンスと比較性を向上させることができます。
出力:
出力は、StandardScalerを適用した後の特徴量MedInc、AveRooms、およびAveOccupのスケーリングされた値を表しています。これらの値は、すべての特徴量が同じ尺度に揃い、平均が0、標準偏差が1になっています。
最初の行[ 2.34476576 0.62855945 -0.04959654]は、最初のデータポイントに対して、スケーリングされたMedIncの値が2.34476576、AveRoomsが0.62855945、AveOccupが-0.04959654であることを示しています。同様に、2行目の[ 2.33223796 0.32704136 -0.09251223]は、2番目のデータポイントのスケーリングされた値を表し、以降も同様です。
スケーリングされた値の範囲は、約-1.14259331から2.34476576までであり、これにより特徴量が正規化および比較可能になりました。入力特徴のスケールに敏感な機械学習モデルでは、大きな範囲を持つ特徴がモデルを支配するのを防ぐために、これは重要です。
複数の線形回帰の実装
データ前処理が完了したので、Pythonで複数の線形回帰を実装しましょう。
train_test_split関数を使用してデータをトレーニングセットとテストセットに分割します。ここでは、データの80%がトレーニングに使用され、20%がテストに使用されます。
モデルは、平均二乗誤差とR二乗を使用して評価されます。平均二乗誤差(MSE)は、誤差または偏差の2乗の平均を測定します。
R二乗(R2)は、回帰モデル内の独立変数によって説明される従属変数の分散の割合を表す統計的指標です。
出力:
上記の出力は、複数の線形回帰モデルのパフォーマンスを評価するための2つの主要な指標を提供します。
平均二乗誤差(MSE): 0.7006855912225249
MSEは、予測値と実際の目的変数値との二乗誤差の平均を測定します。MSEが低いほど、モデルのパフォーマンスが良いことを示し、より正確な予測を行っていることを意味します。この場合、MSEは0.7006855912225249であり、モデルは完璧ではないものの、かなりの精度を持っていることを示しています。通常、MSEの値は0に近いほどよく、より低い値ほどパフォーマンスが良いです。
R二乗値(R2): 0.4652924370503557
R二乗値は、従属変数の分散のうち独立変数から予測可能な部分の割合を測定します。0から1の範囲であり、1は完璧な予測を意味し、0は線形関係がないことを示します。この場合、R二乗値は0.4652924370503557であり、モデルに使用された独立変数によって目的変数の分散の約46.53%が説明できることを示しています。これは、モデルが変数間の関係の重要な部分を捉えることができるが、すべてではないことを示しています。
いくつか重要なプロットを見てみましょう:

.png)
statsmodels
PythonのStatsmodelsライブラリは統計解析に強力なツールです。線形回帰、時系列解析、非パラメトリックな手法など、幅広い統計モデルやテストを提供しています。
複数の線形回帰の文脈では、statsmodelsを使用してデータに線形モデルを適合させ、その後モデルにさまざまな統計テストや分析を行うことができます。これは独立変数と従属変数の関係を理解するのに特に役立ち、モデルに基づいた予測を行うのに役立ちます。
出力:
上記テーブルの要約は次のとおりです:
モデルの要約
モデルは通常最小二乗法回帰モデルであり、線形回帰モデルの一種です。従属変数はMedHouseValueで、モデルのR二乗値は0.485であり、これは約48.5%のMedHouseValueの変動が独立変数によって説明できることを示しています。調整R二乗値は0.484で、これは追加の独立変数を含めることに対してモデルをペナルティするR二乗の修正バージョンです。
モデルの適合度
モデルは最小二乗法を使用して適合され、F統計量は5173であり、モデルが良好に適合していることを示しています。帰無仮説が真であると仮定した場合に観測されるF統計量が少なくとも観測されたものと同じくらい極端である確率は約0です。これは、モデルが統計的に有意であることを示唆しています。
モデル係数
モデルの係数は次のとおりです:
- 定数項は2.0679であり、すべての独立変数が0のときに予測される
MedHouseValueは約2.0679であることを示しています。 x1(この場合MedInc)の係数は0.8300であり、これはMedIncが1単位増加するごとに、他のすべての独立変数が一定であると仮定した場合、予測されるMedHouseValueが約0.83単位増加することを示しています。x2(この場合はAveRooms)の係数は-0.1000であり、x2が1単位増加するごとに、他の独立変数を一定とした場合、予測されるMedHouseValueが約0.10単位減少することを示しています。x3(この場合はAveOccup)の係数は-0.0397であり、x3が1単位増加するごとに、他の独立変数を一定とした場合、予測されるMedHouseValueが約0.04単位減少することを示しています。
モデル診断
モデル診断は以下の通りです:
- Omnibus検定統計量は3981.290であり、残差が正規分布していないことを示しています。
- Durbin-Watson 統計量は1.983であり、残差に有意な自己相関がないことを示しています。
- Jarque-Bera 検定統計量は11583.284であり、残差が正規分布していないことを示しています。
- 残差の歪度は1.260であり、残差が右に偏っていることを示しています。
- 残差の尖度は6.239であり、残差が尖った(つまり、正規分布よりも尖ったピークと重いテールを持つ)ことを示しています。
- 条件数は1.42であり、モデルがデータのわずかな変化に対して敏感でないことを示しています。
.png)
多重共線性の対処
多重共線性は、複数の独立変数が互いに高い相関を持つ多重線形回帰の一般的な問題です。これは、係数の推定値が不安定で信頼性に欠けることにつながる可能性があります。
多重共線性を検出し対処するためには、分散膨張係数を使用できます。VIFは、予測子が相関している場合に推定回帰係数の分散がどれだけ増加するかを測定します。VIFが1の場合、特定の予測子と他の予測子との間に相関がないことを意味します。5または10を超えるVIF値は問題のある共線性の量を示します。
以下のコードブロックでは、モデル内の各独立変数のVIFを計算しましょう。VIF値が5を超える場合、その変数をモデルから削除することを検討する必要があります。
出力:
各特徴のVIF値は以下の通りです:
MedInc: VIF値は1.120166で、他の独立変数との相関が非常に低いことを示しています。これは、MedIncがモデル内の他の独立変数と高度に相関していないことを示しています。AveRooms: VIF値は1.119797で、他の独立変数との相関が非常に低いことを示しています。これは、AveRoomsがモデル内の他の独立変数と高度に相関していないことを示しています。AveOccup:VIF値は1.000488であり、他の独立変数との相関がないことを示しています。これは、AveOccupがモデル内の他の独立変数と相関していないことを示しています。
一般的に、これらのVIF値はすべて5未満であり、モデル内の独立変数間に有意な多重共線性がないことを示しています。これは、モデルが安定して信頼性があり、独立変数の係数が多重共線性によって大きく影響を受けていないことを示しています。
.png)
クロスバリデーション技術
クロスバリデーションは、機械学習モデルのパフォーマンスを評価するために使用される技術です。これは、限られたデータサンプルがある場合にモデルを評価するために使用される再サンプリング手法です。この手順には、kという単一のパラメータがあり、これは与えられたデータサンプルを分割するグループの数を指します。そのため、この手順はしばしばk分割交差検証と呼ばれます。
出力:
クロスバリデーションスコアは、モデルが見知らぬデータでどれだけうまく機能するかを示しています。スコアは0.31191043から0.51269138までの範囲であり、モデルのパフォーマンスが異なる分割で変動していることを示しています。より高いスコアは、より良いパフォーマンスを示します。
平均CV R^2スコアは0.41864482644003276であり、これはモデルが目的変数の分散の約41.86%を平均して説明していることを示しています。これは、モデルが目標変数を予測するのにかなり効果的であることを示す適度な説明レベルであり、さらなる改善や洗練が有益である可能性があります。
これらのスコアは、モデルの一般化能力を評価し、改善のための潜在的な領域を特定するのに使用できます。
.png)
特徴選択手法
再帰的特徴除去メソッドは、指定された数の特徴が達成されるまで、最も重要でない特徴を再帰的に除去する特徴選択テクニックです。このメソッドは、多数の特徴を扱う場合や、最も情報のある特徴のサブセットを選択する目的の場合に特に有用です。
提供されたコードでは、まず、sklearn.feature_selectionからRFEクラスをインポートします。次に、指定されたestimator(この場合、LinearRegression)を使用してRFEのインスタンスを作成し、n_features_to_selectを2に設定して、トップ2つの特徴を選択することを示します。
次に、RFEオブジェクトをスケーリングされた特徴量X_scaledとターゲット変数yに適合させます。 RFEオブジェクトのsupport_属性は、選択された特徴量を示すブールマスクを返します。
特徴量のランキングを可視化するために、特徴量名とそれに対応するランキングを持つDataFrameを作成します。 RFEオブジェクトのranking_属性は、各特徴量のランキングを返し、値が低いほど重要な特徴量を示します。 その後、特徴量のランキング値でソートされた特徴のランキングの棒グラフをプロットします。 このプロットは、モデル内の各特徴量の相対的な重要性を理解するのに役立ちます。
出力:
.png)
上記のチャートに基づいて、最も適した2つの特徴量はMedIncとAveRoomsです。 これは、モデルの出力によっても確認できます。従属変数MedHouseValueは、主にMedIncとAveRoomsに依存しています。
FAQs
Pythonで複数の線形回帰を実装する方法は?
Pythonで複数の線形回帰を実装するには、statsmodelsやscikit-learnなどのライブラリを使用できます。以下はscikit-learnを使用した簡単な概要です:
これにより、モデルの適合、係数の取得、および予測の作成方法が示されます。
Pythonにおける複数の線形回帰の仮定は何ですか?
複数の線形回帰は、有効な結果を保証するためにいくつかの仮定に依存しています:
- 直線性: 予測変数とターゲット変数の関係は直線的であること。
- 独立性: 観測値は互いに独立していること。
- 均一分散性: 残差(エラー)の分散が独立変数のすべてのレベルで一定であること。
- 残差の正規性: 残差が正規分布していること。
- 多重共線性がない: 独立変数同士が高い相関を示していない。
残差プロット、分散膨張係数(VIF)、または統計テストなどのツールを使用してこれらの仮定をテストできます。
Pythonでの多重回帰結果の解釈方法は?
回帰結果からの主要な指標には以下が含まれます:
- 係数(coef_): 他の変数を一定とした場合に、対応する予測子が1単位変化したときの目的変数の変化を示します。
例: X1の係数が2の場合、他の変数を一定とした状態でX1が1単位増加すると、目的変数が2増加します。
2.切片(intercept_): すべての予測子がゼロの場合の目的変数の予測値を表します。
3.R二乗: 予測子によって説明される目的変数の分散の割合を説明します。
例: R^2が0.85の場合、目的変数の85%の変動がモデルによって説明されています。
4.P値(statsmodels内): 予測子の統計的有意性を評価します。通常、p値が0.05未満の場合、予測子が有意であることを示します。
Pythonにおける単回帰と重回帰の違いは何ですか?
| Feature | Simple Linear Regression | Multiple Linear Regression |
|---|---|---|
| 独立変数の数 | 1つ | 複数 |
| モデル方程式 | y = β0 + β1x + ε | y = β0 + β1×1 + β2×2 + … + βnxn + ε |
| 仮定 | 単回帰と同じく複数の独立変数と同じですが、単一の独立変数を持ちます | 単回帰と同じく、ただし複数の独立変数に対する追加の仮定があります |
| 係数の解釈 | 他の変数を一定とした場合の独立変数の単位変化に対する目標変数の変化(単回帰には適用されません) | 他の独立変数を一定とした場合の1つの独立変数の単位変化に対する目標変数の変化 |
| モデルの複雑さ | 複雑でない | 複雑 |
| モデルの柔軟性 | 柔軟でない | 柔軟 |
| 過学習のリスク | 低い | 高い |
| 解釈可能性 | 解釈が容易 | 解釈が難しい |
| 適用性 | 単純な関係に適している | 複数の要因を持つ複雑な関係に適している |
| 例 | 寝室の数に基づいて家の価格を予測する | 寝室の数、平方フィート、および場所に基づいて家の価格を予測する |
結論
この包括的なチュートリアルでは、カリフォルニア住宅データセットを使用して複数線形回帰を実装する方法を学びました。多重共線性、交差検証、特徴量選択、および正則化などの重要な側面に取り組み、各概念を理解するための包括的な知識を提供しました。また、残差、特徴量の重要性、および全体的なモデルのパフォーマンスを示すために可視化を取り入れる方法を学びました。これにより、Pythonで堅牢な回帰モデルを簡単に構築し、これらのスキルを実世界の問題に適用できるようになりました。
Source:
https://www.digitalocean.com/community/tutorials/multiple-linear-regression-python













