الانحدار الخطي المتعدد في لغة البرمجة بايثون: دليل شامل

مقدمة

الانحدار الخطي المتعدد هو تقنية إحصائية أساسية تُستخدم لنمذجة العلاقة بين متغير تابع وعدة متغيرات مستقلة. في Python ، توفر أدوات مثل scikit-learn و statsmodels تنفيذات قوية لتحليل الانحدار. ستقوم هذه الدورة التعليمية بإرشادك خلال تنفيذ وتفسير وتقييم نماذج الانحدار الخطي المتعدد باستخدام Python.

المتطلبات المسبقة

قبل الانغماس في التنفيذ ، تأكد من أن لديك ما يلي:

• فهم أساسي للغة Python. يمكنك الرجوع إلى دورة Python للمبتدئين.
• الإلمام بـ scikit-learn لمهام تعلم الآلة. يمكنك الرجوع إلى دورة Python scikit-learn.
• فهم مفاهيم تصوير البيانات في لغة البرمجة بايثون. يمكنك الرجوع إلى كيفية رسم البيانات في بايثون 3 باستخدام matplotlib و تحليل البيانات وتصويرها باستخدام pandas ودفتر ملاحظات Jupyter في بايثون 3.
• يجب تثبيت Python 3.x مع المكتبات التالية numpy, pandas, matplotlib, seaborn, scikit-learn, و statsmodels.

ما هو الانحدار الخطي المتعدد؟

الانحدار الخطي المتعدد (MLR) هو طريقة إحصائية تقوم بنمذجة العلاقة بين متغير تابع واثنين أو أكثر من المتغيرات المستقلة. إنه تمديد للانحدار الخطي البسيط الذي يقوم بنمذجة العلاقة بين متغير تابع واحد منفصل. في MLR، تتم نمذجة العلاقة باستخدام الصيغة:

حيث:

مثال: توقع سعر منزل بناءً على حجمه، عدد غرف النوم، والموقع. في هذه الحالة، هناك ثلاث متغيرات مستقلة، أي الحجم، عدد غرف النوم، والموقع، ومتغير تابع واحد، أي السعر، الذي يتم التنبؤ به.

افتراضات الانحدار الخطي المتعدد

قبل تنفيذ الانحدار الخطي المتعدد، من الضروري التأكد من تحقق الافتراضات التالية:

1. الخطية: العلاقة بين المتغير التابع والمتغيرات المستقلة هي خطية.

2. استقلال الأخطاء: الباقيات (الأخطاء) مستقلة من بعضها. يتم التحقق من ذلك غالبًا باستخدام اختبار دوربين-واتسون.

3. الهمسكيدية: تكون تباين الباقيات ثابتًا عبر جميع مستويات المتغيرات المستقلة. يمكن أن يساعد رسم الباقيات في التحقق من ذلك.

4. عدم وجود تعدد الانسجام: المتغيرات المستقلة غير مرتبطة بشكل كبير. يُستخدم العامل الانتفاخي للتباين (VIF) بشكل شائع لاكتشاف تعدد الانسجام.

5. الانحراف الطبيعي للباقيات: يجب أن تتبع الباقيات توزيعًا طبيعيًا. يمكن التحقق من ذلك باستخدام مخطط Q-Q.

6. تأثير القيم الشاذة: لا ينبغي أن تؤثر القيم الشاذة أو نقاط الرافعة العالية بشكل مفرط على النموذج.

تضمن هذه الافتراضات أن النموذج الخطي صالح وأن النتائج موثوقة. فشل تحقيق هذه الافتراضات قد يؤدي إلى نتائج غير موضوعية أو مضللة.

قبل معالجة البيانات

في هذا القسم، ستتعلم كيفية استخدام نموذج الانحدار الخطي المتعدد في لغة البرمجة Python لتوقع أسعار المنازل استنادًا إلى الميزات من مجموعة بيانات سكن كاليفورنيا. ستتعلم كيفية معالجة البيانات، وتناسب نموذج الانحدار، وتقييم أدائه مع التعامل مع التحديات الشائعة مثل التعددية، والقيم الشاذة، واختيار الميزات.

الخطوة 1 – تحميل المجموعة البيانات

ستستخدم مجموعة البيانات سكن كاليفورنيا، وهي مجموعة بيانات شهيرة لمهام الانحدار. تحتوي هذه المجموعة على 13 ميزة حول المنازل في ضواحي بوسطن وسعرها المتوسط المقابل.

أولا، دعنا نقوم بتثبيت الحزم الضرورية:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  ‏# استيراد وظيفة fetch_california_housing من مجموعة بيانات sklearn.datasets لتحميل مجموعة بيانات الإسكان في كاليفورنيا.
import pandas as pd  ‏# استيراد pandas لتحليل ومعالجة البيانات.
import numpy as np  ‏# استيراد numpy للحوسبة العددية.

‏# تحميل مجموعة بيانات الإسكان في كاليفورنيا باستخدام وظيفة fetch_california_housing.
housing = fetch_california_housing()

‏# تحويل بيانات مجموعة البيانات إلى DataFrame في pandas، باستخدام أسماء السمات كعناوين للأعمدة.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

‏# إضافة المتغير الهدف 'MedHouseValue' إلى الDataFrame، باستخدام قيم الهدف في مجموعة البيانات.
housing_df['MedHouseValue'] = housing.target

‏# عرض الصفوف الأولى من الDataFrame للحصول على نظرة عامة عن مجموعة البيانات.
print(housing_df.head())

يجب ملاحظة الناتج التالي لمجموعة البيانات:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

وهنا ما تعنيه كل سمة:

الخطوة 2 – معالجة البيانات

التحقق من القيم المفقودة

يضمن عدم وجود قيم مفقودة في مجموعة البيانات التي قد تؤثر على التحليل.

print(housing_df.isnull().sum())

الناتج:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

اختيار الميزات

لنقم أولاً بإنشاء مصفوفة ترابط لفهم الارتباطات بين المتغيرات.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

الناتج:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

يمكنك تحليل مصفوفة الترابط أعلاه لتحديد المتغيرات التابعة والمستقلة لنموذج الانحدار لدينا. توفر مصفوفة الترابط رؤى حول العلاقات بين كل زوج من المتغيرات في مجموعة البيانات.

في المصفوفة الترابطية المعطاة، MedHouseValue هو المتغير التابع، لأنه المتغير الذي نحاول التنبؤ به. المتغيرات المستقلة لها ترابط كبير مع MedHouseValue.

بناءً على مصفوفة الترابط، يمكنك تحديد المتغيرات المستقلة التالية التي لها ترابط كبير مع MedHouseValue:

• MedInc: يمتلك هذا المتغير ترابط إيجابي قوي (0.688075) مع MedHouseValue، مما يشير إلى أنه مع زيادة الدخل الوسيط، يميل قيمة البيوت الوسيطة أيضًا إلى الزيادة.
• AveRooms: يمتلك هذا المتغير ترابط إيجابي معتدل (0.151948) مع MedHouseValue، مما يوحي بأنه كلما زاد عدد الغرف في المنزل الواحد، كلما زادت قيمة البيت الوسيطة أيضًا.
• AveOccup: تحمل هذه المتغيرات ترابط سلبي ضعيف (-0.023737) مع MedHouseValue، مما يشير إلى أنه كلما زادت متوسط الاحتلال لكل منزل، يميل قيمة البيت الوسيطة إلى الانخفاض، لكن التأثير صغير نسبيًا.

من خلال اختيار هذه المتغيرات المستقلة، يمكنك بناء نموذج انحدار يلتقط العلاقات بين هذه المتغيرات وMedHouseValue، مما يتيح لنا عمل توقعات حول قيمة البيت الوسيطة استنادًا إلى الدخل الوسيط، وعدد الغرف الوسطي، والاحتلال الوسطي.

يمكنك أيضًا رسم مصفوفة الترابط في Python باستخدام الكود التالي:

import seaborn as sns
import matplotlib.pyplot as plt

# نفترض أن 'housing_df' هو الإطار البيانات الذي يحتوي على البيانات
# رسم مصفوفة الترابط
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

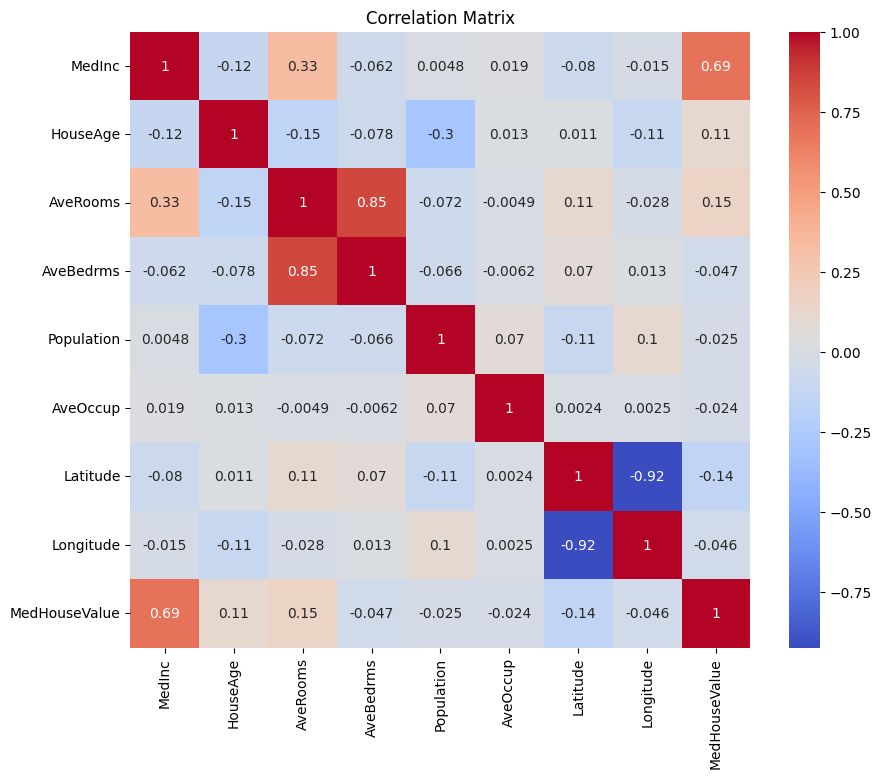
ستركز على بعض الميزات الرئيسية للبساطة استنادًا إلى ما سبق، مثل MedInc (الدخل الوسيط)، AveRooms (متوسط الغرف لكل منزل)، وAveOccup (متوسط الاحتلال لكل منزل).

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

يقوم الكود أعلاه بتحديد ميزات محددة من إطار البيانات housing_df للتحليل. الميزات المحددة هي MedInc، AveRooms، وAveOccup، والتي يتم تخزينها في قائمة selected_features.

يتم ثم تقسيم إطار البيانات housing_df لتشمل فقط هذه الميزات المحددة ويتم تخزين النتيجة في قائمة X.

يتم استخراج المتغير الهدف MedHouseValue من housing_df ويتم تخزينه في القائمة y.

تقييس الميزات

سوف تستخدم عملية التوحيد (Standardization) لضمان أن جميع الميزات على نفس المقياس، مما يعزز أداء النموذج وقابليته للمقارنة.

التوحيد هو تقنية معالجة مسبقة تقوم بتوحيد الميزات الرقمية لتكون لها متوسط قيمة يساوي 0 وانحراف معياري يساوي 1. تضمن هذه العملية أن جميع الميزات على نفس المقياس، وهو أمر ضروري لنماذج التعلم الآلي التي تكون حساسة لمقياس ميزات الإدخال. من خلال توحيد الميزات، يمكنك تحسين أداء النموذج وقابليته للمقارنة عن طريق تقليل تأثير الميزات ذات النطاقات الكبيرة التي تهيمن على النموذج.

from sklearn.preprocessing import StandardScaler

# تهيئة كائن StandardScaler
scaler = StandardScaler()

# تناسب المقياس مع البيانات وتحويله
X_scaled = scaler.fit_transform(X)

# طباعة البيانات المقيَّدة
print(X_scaled)

الناتج:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

الناتج يمثل القيم المقيدة للميزات MedInc، AveRooms، و AveOccup بعد تطبيق StandardScaler. القيم الآن مركزة حول الصفر بانحراف معياري يساوي 1، مما يضمن أن جميع الميزات على نفس المقياس.

الصف الأول [ 2.34476576 0.62855945 -0.04959654] يشير إلى أن قيمة MedInc المقيدة للنقطة البيانات الأولى هي 2.34476576، AveRooms هي 0.62855945، و AveOccup هي -0.04959654. بالمثل، الصف الثاني [ 2.33223796 0.32704136 -0.09251223] يمثل القيم المقيدة للنقطة البيانات الثانية، وهكذا.

القيم المقيّسة تتراوح تقريباً من -1.14259331 إلى 2.34476576، مما يشير إلى أن الميزات تم تطويعها وجعلها قابلة للمقارنة الآن. هذا أمر أساسي لنماذج تعلم الآلة التي تكون حساسة لمقياس ميزات الإدخال، حيث يمنع السماح للميزات ذات النطاقات الكبيرة من السيطرة على النموذج.

نفذ الانحدار الخطي المتعدد

تنفيذ الانحدار الخطي المتعدد

الآن بعد الانتهاء من تجهيز البيانات دعونا نقوم بتنفيذ الانحدار الخطي المتعدد في بايثون.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# يتم تهيئة النموذج 'LinearRegression' وتناسبه مع بيانات التدريب.
model = LinearRegression()
model.fit(X_train, y_train)

# يتم استخدام النموذج لتوقع المتغير الهدف لمجموعة الاختبار.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

يتم استخدام دالة train_test_split لتقسيم البيانات إلى مجموعات تدريب واختبار. هنا، يتم استخدام 80% من البيانات للتدريب و 20% للاختبار.

يتم تقييم النموذج باستخدام خطأ المربعات المتوسطة ومعامل R-squared. يقيس خطأ المربعات المتوسطة (MSE) المتوسط لمربعات الأخطاء أو التحويلات.

معامل R-squared (R2) هو مقياس إحصائي يُمثل النسبة المئوية للتباين لمتغير تابع يُفسره متغير مستقل أو متغيرات في نموذج الانحدار.

الناتج:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

يوفر الناتج أعلاه مقاييس رئيسية اثنتان لتقييم أداء نموذج الانحدار الخطي المتعدد:

معدل الخطأ المربعي (MSE): 0.7006855912225249
MSE يقيس الفرق المربع المتوسط بين القيم المتوقعة والفعلية للمتغير الهدف. يشير MSE الأقل إلى أداء نموذج أفضل، حيث يعني ذلك أن النموذج يقوم بتوقعات أكثر دقة. في هذه الحالة، قيمة MSE هي 0.7006855912225249، مما يشير إلى أن النموذج ليس مثاليًا ولكن لديه مستوى معقول من الدقة. قيم MSE عادة ما تكون أقرب إلى 0، حيث تشير القيم الأقل إلى أداء أفضل.

مربع الارتباط (R-squared): 0.4652924370503557
R-squared يقيس نسبة التباين في المتغير المعتمد القابل للتنبؤ من المتغيرات المستقلة. يتراوح بين 0 و 1، حيث 1 هو التنبؤ المثالي و 0 يشير إلى عدم وجود علاقة خطية. في هذه الحالة، قيمة R-squared هي 0.4652924370503557، مما يشير إلى أن حوالي 46.53٪ من التباين في المتغير الهدف يمكن تفسيره بواسطة المتغيرات المستقلة المستخدمة في النموذج. يقترح ذلك أن النموذج قادر على التقاط جزء كبير من العلاقات بين المتغيرات ولكن ليس كلها.

لنلقي نظرة على بعض الرسوم البيانية الهامة:

# رسم البقايا
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# رسم التوقعات مقابل القيم الفعلية
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

استخدام statsmodels

مكتبة Statsmodels في لغة البرمجة Python هي أداة قوية لتحليل الإحصائيات. توفر مجموعة واسعة من النماذج الإحصائية والاختبارات، بما في ذلك تحليل الانحدار الخطي، وتحليل سلاسل الزمن، والأساليب غير المعلمية.

في سياق تحليل الانحدار الخطي المتعدد، يمكن استخدام statsmodels لتناسب نموذجاً خطياً للبيانات، ثم إجراء مختلف الاختبارات والتحاليل الإحصائية على النموذج. يمكن أن يكون ذلك مفيدًا بشكل خاص لفهم العلاقات بين المتغيرات المستقلة والتابعة، ولعمل توقعات استنادًا إلى النموذج.

import statsmodels.api as sm

# إضافة ثابت إلى النموذج
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# Q-Q Plot للباقي
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

الناتج:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

إليك ملخص الجدول أعلاه:

ملخص النموذج

النموذج هو نموذج تحويلات Ordinary Least Squares، وهو نوع من نماذج التحويلات الخطية. المتغير التابع هو MedHouseValue، والنموذج يحتوي على قيمة R-squared تبلغ 0.485، مما يشير إلى أن حوالي 48.5% من التباين في MedHouseValue يمكن تفسيره بواسطة المتغيرات المستقلة. قيمة R-squared المعدلة هي 0.484، وهي نسخة معدلة من R-squared تعاقب النموذج لاحتوائه على متغيرات مستقلة إضافية.

ملاءمة النموذج

تم تناسب النموذج باستخدام طريقة الأقل مربعات، والإحصاء F هو 5173، مما يشير إلى أن النموذج يتناسب بشكل جيد. احتمال رصد إحصاء F بمقدار على الأقل مثل الذي رصد، بشرط أن فرضية الفراغ صحيحة، يبلغ تقريبًا 0. هذا يقترح أن النموذج ذو دلالة إحصائية.

معاملات النموذج

معاملات النموذج هي كالتالي:

• مصطلح الثابت هو 2.0679، مما يشير إلى أنه عندما تكون جميع المتغيرات المستقلة 0، يكون تنبؤي MedHouseValue تقريبًا 2.0679.
• معامل x1(في هذه الحالة MedInc) هو 0.8300، مما يشير إلى أنه مع كل زيادة في وحدة في MedInc، يزيد تنبؤي MedHouseValue بحوالي 0.83 وحدة، مع افتراض ثبوت جميع المتغيرات المستقلة الأخرى.
• يبلغ معامل x2 (في هذه الحالة AveRooms) -0.1000، مما يشير إلى أنه مع كل زيادة في وحدة في x2، ينخفض MedHouseValue المتوقع بحوالي 0.10 وحدة، بشرط أن تبقى جميع المتغيرات المستقلة الأخرى ثابتة.
• يبلغ معامل x3 (في هذه الحالة AveOccup) -0.0397، مما يشير إلى أنه مع كل زيادة في وحدة في x3، ينخفض MedHouseValue المتوقع بحوالي 0.04 وحدة، بشرط أن تبقى جميع المتغيرات المستقلة الأخرى ثابتة.

تشخيص النموذج

نتائج تشخيص النموذج كما يلي:

• إحصاء اختبار أومنيبوس هو 3981.290، مما يشير إلى أن الباقي غير منتظم بشكل طبيعي.
• إحصاء دربين-واتسون هو 1.983، مما يشير إلى عدم وجود تباين تتبعي significant في الباقي.
• إحصاء اختبار جارك-بيرا هو 11583.284، مما يشير إلى أن الباقي غير منتظم بشكل طبيعي.
• انحراف الباقي هو 1.260، مما يشير إلى أن الباقي مائل لليمين.
• كورتوز الباقي هو 6.239، مما يشير إلى أن الباقي شبه ذو ذروة عالية وذي أذيال أثقل من التوزيع الطبيعي.
• عدد الشرط هو 1.42، مما يشير إلى أن النموذج ليس حساسًا للتغييرات الصغيرة في البيانات.

معالجة تعدد الاندماج

التعدد الخطي هو مشكلة شائعة في الانحدار الخطي المتعدد، حيث تكون هناك علاقة قوية بين اثنين أو أكثر من المتغيرات المستقلة. يمكن أن يؤدي ذلك إلى تقديرات غير مستقرة وغير موثوقة للمعاملات.

لاكتشاف ومعالجة التعدد الخطي، يمكنك استخدام عامل تضخم التباين. يقيس VIF مقدار زيادة التباين في معامل الانحدار المقدر إذا كانت المتغيرات التنبؤية مرتبطة. يعني VIF بقيمة 1 أنه لا توجد علاقة بين متنبئ معين وبقية المتنبئين. تشير قيم VIF التي تتجاوز 5 أو 10 إلى وجود كمية مشكلة من التعدد الخطي.

في الكود أدناه، دعنا نحسب VIF لكل متغير مستقل في نموذجنا. إذا كانت أي قيمة VIF تتجاوز 5، يجب عليك التفكير في إزالة المتغير من النموذج.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# رسم عمودي لقيم VIF
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

الإخراج:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

قيم VIF لكل خاصية هي كما يلي:

• MedInc: قيمة VIF هي 1.120166، مما يشير إلى وجود علاقة منخفضة جداً مع المتغيرات المستقلة الأخرى. وهذا يشير إلى أن MedInc ليست مرتبطة بشكل كبير مع المتغيرات المستقلة الأخرى في النموذج.
• AveRooms: قيمة VIF هي 1.119797، مما يشير إلى وجود علاقة منخفضة جداً مع المتغيرات المستقلة الأخرى. وهذا يشير إلى أن AveRooms ليست مرتبطة بشكل كبير مع المتغيرات المستقلة الأخرى في النموذج.
• AveOccup: قيمة VIF هي 1.000488، مما يشير إلى عدم وجود ترابط مع المتغيرات المستقلة الأخرى. وهذا يوحي بأن AveOccup غير مرتبط بالمتغيرات المستقلة الأخرى في النموذج.

بشكل عام، تكون قيم VIF هذه جميعًا أقل من 5، مما يشير إلى عدم وجود تعددية الانحدار الكبيرة بين المتغيرات المستقلة في النموذج. وهذا يوحي بأن النموذج مستقر وموثوق، وأن معاملات المتغيرات المستقلة لا تتأثر بشكل كبير بالتعددية في الانحدار.

تقنيات التقييم المتقاطع

التقييم المتقاطع هو تقنية تُستخدم لتقييم أداء نموذج تعلم الآلة. إنه إجراء إعادة عينة يُستخدم لتقييم نموذج إذا كان لدينا عينة بيانات محدودة. الإجراء له معلمة واحدة تُسمى k تشير إلى عدد المجموعات التي يجب تقسيم عينة البيانات المعطاة إليها. ولذلك، يُطلق على الإجراء كثنائي التقييم المتقاطع.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# رسم الخط لعلامات التقييم المتقاطع
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

الإخراج:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

تشير علامات التقييم المتقاطع إلى كيفية أداء النموذج على البيانات غير المرئية. تتراوح العلامات بين 0.31191043 و 0.51269138، مما يشير إلى تغير أداء النموذج عبر الطيات المختلفة. تشير العلامة العالية إلى أداء أفضل.

متوسط نقطة CV R^2 هو 0.41864482644003276، مما يشير إلى أن النموذج يفسر بمتوسط حوالي 41.86٪ من التباين في المتغير المستهدف. هذا مستوى معتدل من الشرح، مما يدل على أن النموذج فعال إلى حد ما في توقع المتغير المستهدف ولكن قد يستفيد من تحسين أو تنقيح إضافي.

يمكن استخدام هذه النتائج لتقييم قابلية تعميم النموذج وتحديد المجالات المحتملة للتحسين.

طرق اختيار الميزات

طريقة الإقصاء التلقائي للميزات هي تقنية اختيار الميزات التي تقوم بإزالة الميزات الأقل أهمية بشكل تكراري حتى يتم الوصول إلى عدد محدد من الميزات. تكون هذه الطريقة مفيدة بشكل خاص عند التعامل مع عدد كبير من الميزات والهدف هو اختيار مجموعة من الميزات الأكثر إفادة.

في الشفرة المقدمة، يتم استيراد فئة RFE أولاً من sklearn.feature_selection. ثم يتم إنشاء مثيل من RFE بمقدار محدد للمقدر (في هذه الحالة، LinearRegression) وتعيين n_features_to_select إلى 2، مما يشير إلى رغبتنا في اختيار أفضل 2 ميزة.

بعد ذلك، نقوم بملاءمة كائن RFE مع ميزاتنا المقيَّسة X_scaled والمتغير الهدف y. يُرجع السمة support_ لكائن RFE قناعًا بوليانيًا يشير إلى السمات التي تم اختيارها.

لتصوير تصنيف الميزات، قم بإنشاء إطار بيانات باسماء الميزات وتصنيفاتها المقابلة. تُرجع السمة ranking_ لكائن RFE تصنيف كل ميزة، حيث تشير القيم الأقل إلى الميزات الأكثر أهمية. ثم قم برسم رسم بياني شريطي لتصنيف الميزات، مرتبًا حسب قيم التصنيف الخاصة بها. يساعد هذا الرسم في فهم الأهمية النسبية لكل ميزة في النموذج.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# رسم بياني لتصنيف الميزات
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

الناتج:

Selected Features: [ True  True False]

بناءً على الرسم البياني أعلاه، تعتبر أكثر ميزتين مناسبة هما MedInc و AveRooms. يمكن التحقق من ذلك أيضًا من إخراج النموذج أعلاه حيث يعتمد المتغير التابع MedHouseValue بشكل كبير على MedInc و AveRooms.

الأسئلة الشائعة

كيفية تنفيذ الانحدار الخطي المتعدد في Python؟

لتنفيذ الانحدار الخطي المتعدد في Python ، يمكنك استخدام مكتبات مثل statsmodels أو scikit-learn. إليك نظرة عامة سريعة باستخدام scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# بيانات مثالية
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # المتغيرات العاملة
y = np.array([5, 7, 9, 11])  # المتغير المستهدف

# إنشاء وتدريب النموذج
model = LinearRegression()
model.fit(X, y)

# الحصول على معاملات وتقاطع
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# عمل توقعات
predictions = model.predict(X)
print("Predictions:", predictions)

هذا يوضح كيفية تدريب النموذج والحصول على المعاملات وعمل التوقعات.

ما هي افتراضات الانحدار الخطي المتعدد في Python؟

يعتمد الانحدار الخطي المتعدد على عدة افتراضات لضمان النتائج الصحيحة:

1. الخطية: العلاقة بين المتغيرات العاملة والمتغير المستهدف خطية.
2. الاستقلالية: الرصد غير مترابطة مع بعضها البعض.
3. الهوموسيداستيسية: تكون تباين الباقيات (الأخطاء) ثابتة عبر جميع مستويات المتغيرات المستقلة.
4. الانحدار الطبيعي للباقيات: الباقيات موزعة بشكل طبيعي.
5. لا توجد تعددية في التعلق: المتغيرات المستقلة ليست مرتبطة تمامًا ببعضها البعض.

يمكنك اختبار هذه الافتراضات باستخدام أدوات مثل الرسوم البيانية للباقي، معامل تضخم التباين (VIF)، أو الاختبارات الإحصائية.

كيف يمكنك تفسير نتائج التحويلات المتعددة في Python؟

المقاييس الرئيسية من نتائج التحويلات تشمل:

1. المعاملات (coef_): تشير إلى التغيير في المتغير الهدف لوحدة التغيير في العامل التنبؤي المقابل، مع الحفاظ على المتغيرات الأخرى ثابتة.

مثال: معامل قيمته 2 لـ X1 يعني أن المتغير الهدف يزيد بمقدار 2 لكل زيادة بوحدة واحدة في X1، مع الحفاظ على المتغيرات الأخرى ثابتة.

2.التقاطع (intercept_): يمثل القيمة المتوقعة للمتغير الهدف عندما تكون جميع العوامل تنبؤية على الصفر.

3.R-squared: يشرح نسبة التباين في المتغير الهدف يتم شرحها بواسطة العوامل التنبؤية.

مثال: R^2 بقيمة 0.85 يعني أن 85% من التغير في المتغير الهدف يتم شرحه بواسطة النموذج.

4.قيم P (في statsmodels): تقييم الأهمية الإحصائية للعوامل التنبؤية. قيمة P < 0.05 عادة ما تشير إلى أن العامل التنبؤي ذو أهمية.

ما الفرق بين الانحدار الخطي البسيط والمتعدد في Python؟

الاستنتاج

في هذا البرنامج التعليمي الشامل، تعلمت كيفية تنفيذ الانحدار الخطي المتعدد باستخدام مجموعة بيانات الإسكان في كاليفورنيا. لقد تناولت جوانب حاسمة مثل التعدد الخطي بين المتغيرات، التقييم المتقاطع، اختيار الميزات، والتنظيم، مما قدم لك فهماً شاملاً لكل مفهوم. كما تعلمت كيفية دمج التصورات البصرية لتوضيح الباقيات، أهمية الميزات، وأداء النموذج بشكل عام. يمكنك الآن بناء نماذج انحدارية قوية بسهولة باستخدام Python وتطبيق هذه المهارات على مشاكل العالم الحقيقي.