Множественная линейная регрессия в Python: Подробное руководство

Python

Введение

Множественная линейная регрессия — это фундаментальная статистическая техника, используемая для моделирования зависимости между одной зависимой переменной и несколькими независимыми переменными. В Python такие инструменты, как scikit-learn и statsmodels, предоставляют надежные реализации для анализа регрессии. Этот учебник проведет вас через реализацию, интерпретацию и оценку моделей множественной линейной регрессии с использованием Python.

Предварительные требования

Перед тем как погрузиться в реализацию, убедитесь, что у вас есть следующее:

Базовое понимание Python. Вы можете обратиться к Учебнику по Python для начинающих.
Знакомство с scikit-learn для задач машинного обучения. Вы можете обратиться к Учебнику по scikit-learn на Python.
Понимание концепций визуализации данных в Python. Вы можете обратиться к Как построить графики в Python 3 с использованием matplotlib и Анализ данных и визуализация с помощью pandas и Jupyter Notebook в Python 3.
Установлен Python 3.x с следующими библиотеками numpy, pandas, matplotlib, seaborn, scikit-learn и statsmodels.

Что такое множественная линейная регрессия?

Множественная линейная регрессия (MLR) — это статистический метод, который моделирует взаимосвязь между зависимой переменной и двумя или более независимыми переменными. Это расширение простой линейной регрессии, которая моделирует взаимосвязь между зависимой переменной и одной независимой переменной. В MLR взаимосвязь моделируется с использованием формулы:

Где:

Пример: предсказание цены дома на основе его размера, количества спален и местоположения. В этом случае есть три независимые переменные, т.е. размер, количество спален и местоположение, и одна зависимая переменная, т.е. цена, которая является значением, подлежащим прогнозированию.

Предположения множественной линейной регрессии

Перед применением множественной линейной регрессии важно убедиться, что выполнены следующие предположения:

Линейность: Связь между зависимой переменной и независимыми переменными линейная.
Независимость ошибок: Остатки (ошибки) независимы друг от друга. Это часто проверяется с помощью критерия Дарбина-Уотсона.
Гомоскедастичность: Дисперсия остатков постоянна на всех уровнях независимых переменных. График остатков может помочь в проверке этого.
Нет мультиколлинеарности: Независимые переменные не сильно коррелированы. Фактор инфляции дисперсии (VIF) обычно используется для обнаружения мультиколлинеарности.
Нормальность остатков: Остатки должны следовать нормальному распределению. Это можно проверить с помощью Q-Q графика.
Влияние выбросов: Выбросы или точки с высокой влиянием не должны непропорционально влиять на модель.

Эти предположения обеспечивают корректность регрессионной модели и надежность результатов. Невыполнение этих предположений может привести к искаженным или вводящим в заблуждение результатам.

Предварительная обработка данных

В этом разделе вы узнаете, как использовать модель множественной линейной регрессии в Python для прогнозирования цен на дома на основе характеристик из Набора данных о жилье в Калифорнии. Вы узнаете, как предварительно обрабатывать данные, подгонять регрессионную модель и оценивать ее производительность, учитывая распространенные проблемы, такие как мультиколлинеарность, выбросы и выбор признаков.

Шаг 1 – Загрузка набора данных

Вы будете использовать Набор данных о жилье в Калифорнии, популярный набор данных для задач регрессии. Этот набор данных содержит 13 признаков о домах в пригородах Бостона и соответствующую им медианную цену дома.

Сначала установим необходимые пакеты:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # Импортируйте функцию fetch_california_housing из sklearn.datasets для загрузки набора данных о жилье в Калифорнии.
import pandas as pd  # Импортируйте pandas для манипуляций с данными и анализа.
import numpy as np  # Импортируйте numpy для численных вычислений.

# Загрузите набор данных о жилье в Калифорнии с помощью функции fetch_california_housing.
housing = fetch_california_housing()

# Преобразуйте данные набора данных в DataFrame pandas, используя имена признаков в качестве заголовков столбцов.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# Добавьте целевую переменную 'MedHouseValue' в DataFrame, используя целевые значения набора данных.
housing_df['MedHouseValue'] = housing.target

# Отобразите первые несколько строк DataFrame, чтобы получить общее представление о наборе данных.
print(housing_df.head())

Вы должны увидеть следующий вывод набора данных:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

Вот что означает каждый из атрибутов:

Variable	Description
MedInc	Медианный доход в районе
HouseAge	Медианный возраст домов в районе
AveRooms	Среднее количество комнат
AveBedrms	Среднее количество спален
Population	Население района
AveOccup	Средняя заполняемость домов
Latitude	Широта района домов
Longitude	Долгота района домов

Шаг 2 – Предобработка данных

Проверка на пропущенные значения

Обеспечивает отсутствие пропущенных значений в наборе данных, которые могут повлиять на анализ.

print(housing_df.isnull().sum())

Вывод:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

Выбор признаков

Сначала создадим матрицу корреляции, чтобы понять зависимости между переменными.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

Вывод:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

Вы можете проанализировать вышеуказанную матрицу корреляции, чтобы выбрать зависимые и независимые переменные для нашей регрессионной модели. Матрица корреляции предоставляет представление о взаимосвязях между каждой парой переменных в наборе данных.

В данной матрице корреляции MedHouseValue является зависимой переменной, так как это переменная, которую мы пытаемся предсказать. Независимые переменные имеют значительную корреляцию с MedHouseValue.

На основе матрицы корреляции вы можете выделить следующие независимые переменные, которые имеют значительную корреляцию с MedHouseValue:

MedInc: Эта переменная имеет сильную положительную корреляцию (0.688075) с MedHouseValue, что указывает на то, что с увеличением медианного дохода также стремится увеличиваться медианная стоимость дома.
AveRooms: Эта переменная имеет умеренную положительную корреляцию (0.151948) с MedHouseValue, что предполагает, что с увеличением среднего числа комнат на домохозяйство медианная стоимость дома также стремится увеличиваться.
AveOccup: Эта переменная имеет слабую отрицательную корреляцию (-0.023737) с MedHouseValue, что указывает на то, что с увеличением средней заселенности домохозяйства средняя стоимость дома имеет тенденцию к снижению, но эффект относительно небольшой.

Выбрав эти независимые переменные, вы можете построить регрессионную модель, которая отражает взаимосвязи между этими переменными и MedHouseValue, что позволяет нам делать прогнозы о средней стоимости дома на основе медианного дохода, среднего количества комнат и средней заселенности.

Вы также можете построить матрицу корреляции в Python, используя следующий код:

import seaborn as sns
import matplotlib.pyplot as plt

# Предполагая, что 'housing_df' - это DataFrame, содержащий данные
# Построение матрицы корреляции
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

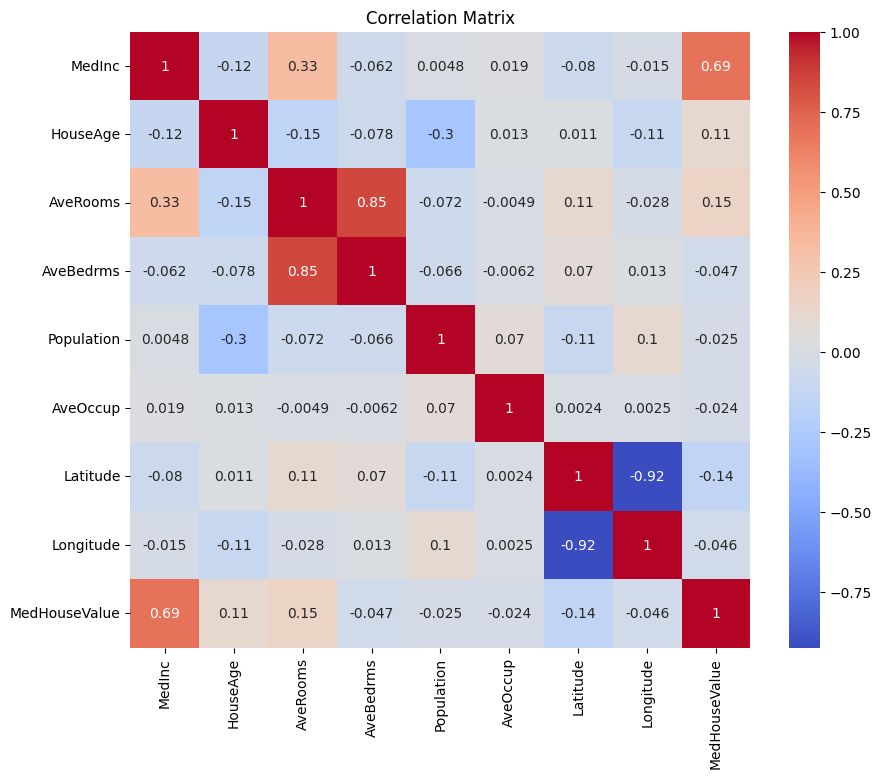
Вы сосредоточитесь на нескольких ключевых функциях для простоты, таких как MedInc (медианный доход), AveRooms (среднее количество комнат на дом) и AveOccup (средняя заселенность домохозяйства) на основе вышеуказанного.

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

Вышеприведенный блок кода выбирает определенные функции из фрейма данных housing_df для анализа. Выбранные функции – MedInc, AveRooms и AveOccup, которые хранятся в списке selected_features.

Затем фрейм данных housing_df сокращается, чтобы включить только эти выбранные функции, и результат сохраняется в списке X.

Целевая переменная MedHouseValue извлекается из housing_df и сохраняется в списке y.

Масштабирование функций

Вы будете использовать стандартизацию, чтобы гарантировать, что все признаки находятся на одной шкале, что улучшит производительность модели и сопоставимость.

Стандартизация — это метод предварительной обработки, который масштабирует числовые признаки так, чтобы их среднее значение было 0, а стандартное отклонение — 1. Этот процесс гарантирует, что все признаки находятся на одной шкале, что необходимо для моделей машинного обучения, чувствительных к шкале входных признаков. Стандартизируя признаки, вы можете улучшить производительность модели и сопоставимость, уменьшая влияние признаков с большими диапазонами, доминирующих в модели.

from sklearn.preprocessing import StandardScaler

# Инициализация объекта StandardScaler
scaler = StandardScaler()

# Подгонка скейлера к данным и преобразование
X_scaled = scaler.fit_transform(X)

# Печать масштабированных данных
print(X_scaled)

Вывод:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

Вывод представляет собой масштабированные значения признаков MedInc, AveRooms и AveOccup после применения StandardScaler. Значения теперь центрированы вокруг 0 со стандартным отклонением 1, что обеспечивает одинаковую шкалу для всех признаков.

Первая строка [ 2.34476576 0.62855945 -0.04959654] указывает на то, что для первой точки данных масштабированное значение MedInc составляет 2.34476576, AveRooms — 0.62855945, а AveOccup — -0.04959654. Аналогично, вторая строка [ 2.33223796 0.32704136 -0.09251223] представляет собой масштабированные значения для второй точки данных и так далее.

Масштабированные значения варьируются примерно от -1.14259331 до 2.34476576, что указывает на то, что признаки теперь нормализованы и сравнимы. Это важно для моделей машинного обучения, которые чувствительны к масштабу входных признаков, поскольку это предотвращает доминирование признаков с большими диапазонами в модели.

Реализация множественной линейной регрессии

Теперь, когда вы завершили предварительную обработку данных, давайте реализуем множественную линейную регрессию на Python.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# Модель 'LinearRegression' инициализируется и подгоняется к обучающим данным.
model = LinearRegression()
model.fit(X_train, y_train)

# Модель используется для предсказания целевой переменной для тестового набора.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

Функция train_test_split используется для разделения данных на обучающую и тестовую выборки. Здесь 80% данных используется для обучения, а 20% для тестирования.

Модель оценивается с использованием среднеквадратичной ошибки и коэффициента детерминации R-квадрат. Среднеквадратичная ошибка (MSE) измеряет среднее значение квадратов ошибок или отклонений.

Коэффициент детерминации R-квадрат (R2) является статистическим показателем, который представляет собой долю дисперсии зависимой переменной, объясняемой независимой переменной или переменными в регрессионной модели.

Вывод:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

Вывод выше предоставляет две ключевые метрики для оценки производительности модели множественной линейной регрессии:

Среднеквадратическая ошибка (MSE): 0.7006855912225249
MSE измеряет среднее квадратное отклонение между предсказанными и фактическими значениями целевой переменной. Более низкое значение MSE указывает на лучшее качество модели, поскольку это означает, что модель делает более точные предсказания. В данном случае MSE составляет 0.7006855912225249, что указывает на то, что модель не идеальна, но имеет разумный уровень точности. Значения MSE обычно должны быть ближе к 0, при этом более низкие значения указывают на лучшее качество.

Коэффициент детерминации (R2): 0.4652924370503557
Коэффициент детерминации измеряет долю дисперсии зависимой переменной, которая может быть предсказана независимыми переменными. Он варьируется от 0 до 1, где 1 означает идеальное предсказание, а 0 указывает на отсутствие линейной зависимости. В данном случае значение R-квадрат составляет 0.4652924370503557, что указывает на то, что примерно 46.53% дисперсии целевой переменной может быть объяснено независимыми переменными, используемыми в модели. Это предполагает, что модель способна захватывать значительную часть взаимосвязей между переменными, но не все из них.

Давайте посмотрим на некоторые важные графики:

# График остатков
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# График предсказанных и фактических значений
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

Использование `statsmodels`

Библиотека Statsmodels в Python является мощным инструментом для статистического анализа. Она предоставляет широкий спектр статистических моделей и тестов, включая линейную регрессию, анализ временных рядов и непараметрические методы.

В контексте множественной линейной регрессии statsmodels можно использовать для подгонки линейной модели к данным, а затем выполнять различные статистические тесты и анализы модели. Это может быть особенно полезно для понимания взаимосвязей между независимыми и зависимыми переменными, а также для делания прогнозов на основе модели.

import statsmodels.api as sm

# Добавление константы к модели
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# Q-Q график для остатков
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

Вывод:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

Здесь представлено резюме вышеуказанной таблицы:

Сводка модели

Модель является обычной линейной регрессией, которая представляет собой тип линейной регрессионной модели. Зависимая переменная – это MedHouseValue, а значение R-квадрат составляет 0.485, что указывает на то, что около 48.5% вариации в MedHouseValue можно объяснить независимыми переменными. Скорректированное значение R-квадрат составляет 0.484, что является модифицированной версией R-квадрат, которая штрафует модель за включение дополнительных независимых переменных.

Подгонка модели

Модель была подогнана с использованием метода наименьших квадратов, а F-статистика составляет 5173, что указывает на то, что модель хорошо подходит. Вероятность наблюдения F-статистики, как минимум такой же экстремальной, как наблюдаемая, при условии, что нулевая гипотеза верна, составляет примерно 0. Это предполагает, что модель статистически значима.

Коэффициенты модели

Коэффициенты модели следующие:

Константный термин равен 2.0679, что указывает на то, что когда все независимые переменные равны 0, предсказанное значение MedHouseValue составляет примерно 2.0679.
Коэффициент для x1 (в данном случае MedInc) составляет 0.8300, что указывает на то, что при увеличении MedInc на одну единицу предсказанное значение MedHouseValue увеличивается примерно на 0.83 единицы, при условии, что все остальные независимые переменные остаются постоянными.
Коэффициент для x2 (в данном случае AveRooms) составляет -0,1000, что указывает на то, что при увеличении x2 на одну единицу прогнозируемое значение MedHouseValue уменьшается примерно на 0,10 единиц, при условии, что все остальные независимые переменные остаются постоянными.
Коэффициент для x3 (в данном случае AveOccup) составляет -0,0397, что указывает на то, что при увеличении x3 на одну единицу прогнозируемое значение MedHouseValue уменьшается примерно на 0,04 единицы, при условии, что все остальные независимые переменные остаются постоянными.

Диагностика модели

Диагностика модели выглядит следующим образом:

Статистика теста Омнибус равна 3981,290, что указывает на то, что остатки не имеют нормального распределения.
Статистика Дарбина-Уотсона равна 1,983, что указывает на отсутствие значительной автокорреляции в остатках.
Статистика теста Жарка-Бера равна 11583,284, что указывает на то, что остатки не имеют нормального распределения.
Асимметрия остатков равна 1,260, указывая на то, что остатки смещены вправо.
Эксцесс остатков равен 6,239, указывая на лептокуртозность остатков (т.е. у них более высокий пик и более тяжелые хвосты, чем у нормального распределения).
Число обусловленности равно 1,42, указывая на то, что модель не чувствительна к небольшим изменениям в данных.

Обработка мультиколлинеарности

Мультиколлинеарность является распространенной проблемой в множественной линейной регрессии, когда две или более независимые переменные сильно коррелируют друг с другом. Это может привести к нестабильным и ненадежным оценкам коэффициентов.

Для обнаружения и устранения мультиколлинеарности вы можете использовать Фактор Инфляции Дисперсии. VIF измеряет, насколько увеличивается дисперсия оцененного коэффициента регрессии, если ваши предикторы коррелируют. Значение VIF равное 1 означает, что нет корреляции между данным предиктором и остальными предикторами. Значения VIF, превышающие 5 или 10, указывают на проблематичное количество коллинеарности.

В блоке кода ниже мы рассчитаем VIF для каждой независимой переменной в нашей модели. Если любое значение VIF превышает 5, вам следует рассмотреть возможность удаления переменной из модели.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# Гистограмма для значений VIF
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

Вывод:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

Значения VIF для каждой характеристики следующие:

MedInc: Значение VIF равно 1.120166, что указывает на очень низкую корреляцию с другими независимыми переменными. Это говорит о том, что MedInc не сильно коррелирует с другими независимыми переменными в модели.
AveRooms: Значение VIF равно 1.119797, что указывает на очень низкую корреляцию с другими независимыми переменными. Это говорит о том, что AveRooms не сильно коррелирует с другими независимыми переменными в модели.
AveOccup: Значение VIF равно 1.000488, что указывает на отсутствие корреляции с другими независимыми переменными. Это говорит о том, что AveOccup не коррелирует с другими независимыми переменными в модели.

В целом, все эти значения VIF ниже 5, что указывает на отсутствие значительной мультиколлинеарности между независимыми переменными в модели. Это свидетельствует о том, что модель стабильна и надежна, и коэффициенты независимых переменных не значительно зависят от мультиколлинеарности.

Техники кросс-валидации

Кросс-валидация – это техника, используемая для оценки производительности модели машинного обучения. Это процедура повторного выбора, используемая для оценки модели, если у нас есть ограниченная выборка данных. Процедура имеет единственный параметр, называемый k, который относится к количеству групп, на которые должна быть разделена данная выборка данных. Поэтому процедуру часто называют кросс-валидацией k-fold.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# Линейный график для оценок кросс-валидации
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

Вывод:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

Оценки кросс-валидации показывают, насколько хорошо модель работает на невидимых данных. Оценки варьируются от 0.31191043 до 0.51269138, что указывает на то, что производительность модели различается для разных фолдов. Более высокая оценка указывает на лучшую производительность.

Среднее значение R^2 для кросс-валидации составляет 0.41864482644003276, что указывает на то, что в среднем модель объясняет около 41.86% дисперсии целевой переменной. Это умеренный уровень объяснения, что свидетельствует о том, что модель довольно эффективно предсказывает целевую переменную, но может получить выгоду от дальнейшего улучшения или доработки.

Эти оценки могут быть использованы для оценки обобщаемости модели и выявления потенциальных областей для улучшения.

Методы выбора признаков

Метод Рекурсивного исключения признаков является техникой выбора признаков, которая рекурсивно исключает наименее важные признаки, пока не будет достигнуто указанное количество признаков. Этот метод особенно полезен при работе с большим количеством признаков, когда цель состоит в том, чтобы выбрать подмножество наиболее информативных признаков.

В предоставленном коде вы сначала импортируете класс RFE из sklearn.feature_selection. Затем создаете экземпляр RFE с указанным оценщиком (в данном случае LinearRegression) и устанавливаете n_features_to_select равным 2, что указывает на то, что мы хотим выбрать 2 лучших признака.

Затем мы подгоняем объект RFE к нашим масштабированным функциям X_scaled и целевой переменной y. Атрибут support_ объекта RFE возвращает булевую маску, указывающую, какие функции были выбраны.

Для визуализации ранжирования функций вы создаете DataFrame с названиями функций и их соответствующими рангами. Атрибут ranking_ объекта RFE возвращает ранжирование каждой функции, при этом более низкие значения указывают на более важные функции. Затем вы строите столбчатую диаграмму ранжирования функций, отсортированных по значениям их рангов. Этот график помогает нам понять относительную важность каждой функции в модели.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# Диаграмма ранжирования функций
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

Output:

Selected Features: [ True  True False]

Исходя из вышеуказанной диаграммы, 2 наиболее подходящие функции – это MedInc и AveRooms. Это также можно подтвердить выводами модели выше, так как зависимая переменная MedHouseValue в основном зависит от MedInc и AveRooms.

ЧаВО

Как реализовать множественную линейную регрессию в Python?

Чтобы реализовать множественную линейную регрессию в Python, вы можете использовать такие библиотеки, как statsmodels или scikit-learn. Вот краткий обзор с использованием scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# Пример данных
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # Предикторные переменные
y = np.array([5, 7, 9, 11])  # Целевая переменная

# Создать и подогнать модель
model = LinearRegression()
model.fit(X, y)

# Получить коэффициенты и интерсепт
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# Сделать прогнозы
predictions = model.predict(X)
print("Predictions:", predictions)

Это демонстрирует, как подогнать модель, получить коэффициенты и сделать прогнозы.

Каковы предположения множественной линейной регрессии в Python?

Множественная линейная регрессия основывается на нескольких предположениях для обеспечения достоверных результатов:

Линейность: Связь между предикторами и целевой переменной линейна.
Независимость: Наблюдения независимы друг от друга.
Гомоскедастичность: Дисперсия остатков (ошибок) постоянна на всех уровнях независимых переменных.
Нормальность остатков: Остатки нормально распределены.
Нет мультиколлинеарности: Независимые переменные не имеют высокой корреляции друг с другом.

Вы можете проверить эти предположения, используя инструменты, такие как остаточные графики, коэффициент инфляции дисперсии (VIF) или статистические тесты.

Как интерпретировать результаты множественной регрессии в Python?

Ключевые метрики из результатов регрессии включают:

Коэффициенты (coef_): Указывают на изменение целевой переменной при изменении соответствующего предиктора на единицу, при прочих равных условиях.

Пример: Коэффициент 2 для X1 означает, что целевая переменная увеличивается на 2 при увеличении X1 на 1, при прочих равных условиях.

2.Пересечение (intercept_): Представляет собой предсказанное значение целевой переменной, когда все предикторы равны нулю.

3.R-квадрат: Объясняет долю дисперсии в целевой переменной, объясняемую предикторами.

Пример: R^2 равно 0.85 означает, что 85% изменчивости в целевой переменной объясняется моделью.

4.P-значения (в statsmodels): Оценивают статистическую значимость предикторов. P-значение < 0.05 обычно указывает на то, что предиктор значим.

В чем разница между простой и множественной линейной регрессией в Python?

Feature	Simple Linear Regression	Multiple Linear Regression
Количество независимых переменных	Одна	Более одной
Уравнение модели	y = β0 + β1x + ε	y = β0 + β1×1 + β2×2 + … + βnxn + ε
Предположения	Те же, что и у множественной линейной регрессии, но с одной независимой переменной	Те же, что и у простой линейной регрессии, но с дополнительными предположениями для нескольких независимых переменных
Интерпретация коэффициентов	Изменение целевой переменной при изменении независимой переменной на единицу, при условии постоянства всех остальных переменных (не применимо в простой линейной регрессии)	Изменение целевой переменной при изменении одной независимой переменной на единицу, при условии постоянства всех остальных независимых переменных
Сложность модели	Меньше сложности	Больше сложности
Гибкость модели	Менее гибкая	Более гибкая
Риск переобучения	Ниже	Выше
Интерпретируемость	Легче интерпретировать	Более сложно интерпретировать
Применимость	Подходит для простых отношений	Подходит для сложных отношений с несколькими факторами
Пример	Прогнозирование цен на дома на основе количества спален	Прогнозирование цен на дома на основе количества спален, площади и местоположения

Вывод

В этом исчерпывающем учебнике вы научились реализовывать множественную линейную регрессию, используя набор данных о жилье в Калифорнии. Вы рассмотрели важные аспекты, такие как мультиколлинеарность, кросс-валидация, выбор признаков и регуляризация, что обеспечило глубокое понимание каждого концепта. Вы также научились включать визуализации для иллюстрации остатков, важности признаков и общей производительности модели. Теперь вы легко можете создавать надежные регрессионные модели на Python и применять эти навыки к задачам реального мира.

Source:
https://www.digitalocean.com/community/tutorials/multiple-linear-regression-python