Python中的多元线性回归：全面指南

教程
Python

介绍

多元线性回归是一种基本的统计技术，用于建模一个因变量与多个自变量之间的关系。在Python中，诸如scikit-learn和statsmodels这样的工具提供了强大的回归分析实现。本教程将指导您如何使用Python实现、解释和评估多元线性回归模型。

先决条件

在开始实现之前，请确保具备以下条件：

什么是多元线性回归？

多元线性回归（MLR）是一种统计方法，用于建模因变量与两个或多个自变量之间的关系。它是简单线性回归的扩展，简单线性回归是用于建模因变量与单个自变量之间的关系。在 MLR 中，关系是使用以下公式建模的：

其中：

示例：根据房屋大小、卧室数量和位置来预测房屋价格。在这种情况下，有三个自变量，即大小、卧室数量和位置，以及一个因变量，即价格，即要预测的值。

多元线性回归的假设

在实施多元线性回归之前，必须确保满足以下假设：

  1. 线性关系：因变量与自变量之间的关系是线性的。

  2. 误差的独立性：残差（误差）彼此独立。通常使用Durbin-Watson检验来验证。

  3. 同方差性：残差的方差在所有自变量的水平上都是恒定的。残差图可帮助验证这一点。

  4. 无多重共线性：自变量之间不高度相关。常用方差膨胀因子（VIF）来检测多重共线性。

  5. 残差的正态性：残差应该服从正态分布。可以通过Q-Q图来检查。

  6. 异常值影响：异常值或高杠杆点不应该对模型产生不成比例的影响。

这些假设确保回归模型是有效的，结果是可靠的。未能满足这些假设可能导致结果存在偏差或误导性。

数据预处理

在这一部分，您将学习如何在Python中使用多元线性回归模型根据加利福尼亚房屋数据集的特征来预测房屋价格。您将学习如何预处理数据、拟合回归模型，并评估其性能，同时解决多重共线性、离群值和特征选择等常见挑战。

步骤1 – 加载数据集

您将使用加利福尼亚房屋数据集，这是一个用于回归任务的流行数据集。该数据集包含了有关波士顿近郊房屋的13个特征以及它们对应的房屋中位价。

首先，让我们安装必要的软件包：

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  从sklearn.datasets中导入fetch_california_housing函数以加载加利福尼亚房屋数据集。
import pandas as pd  导入pandas进行数据操作和分析。
import numpy as np  导入numpy进行数值计算。

使用fetch_california_housing函数加载加利福尼亚房屋数据集。
housing = fetch_california_housing()

将数据集的数据转换为pandas DataFrame，使用特征名称作为列标题。
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

使用数据集的目标值将目标变量“MedHouseValue”添加到DataFrame中。
housing_df['MedHouseValue'] = housing.target

显示DataFrame的前几行，以获取数据集的概览。
print(housing_df.head())

您应该观察到数据集的以下输出：

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

以下是每个属性的含义：

Variable Description
MedInc 区块内的收入中位数
HouseAge 区块内房屋年龄中位数
AveRooms 平均房间数
AveBedrms 平均卧室数
Population 区块人口数
AveOccup 平均住户数
Latitude 房屋区块纬度
Longitude 房屋区块经度

步骤2 – 数据预处理

检查缺失值

确保数据集中没有缺失值，这可能会影响分析结果。

print(housing_df.isnull().sum())

输出：

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

特征选择

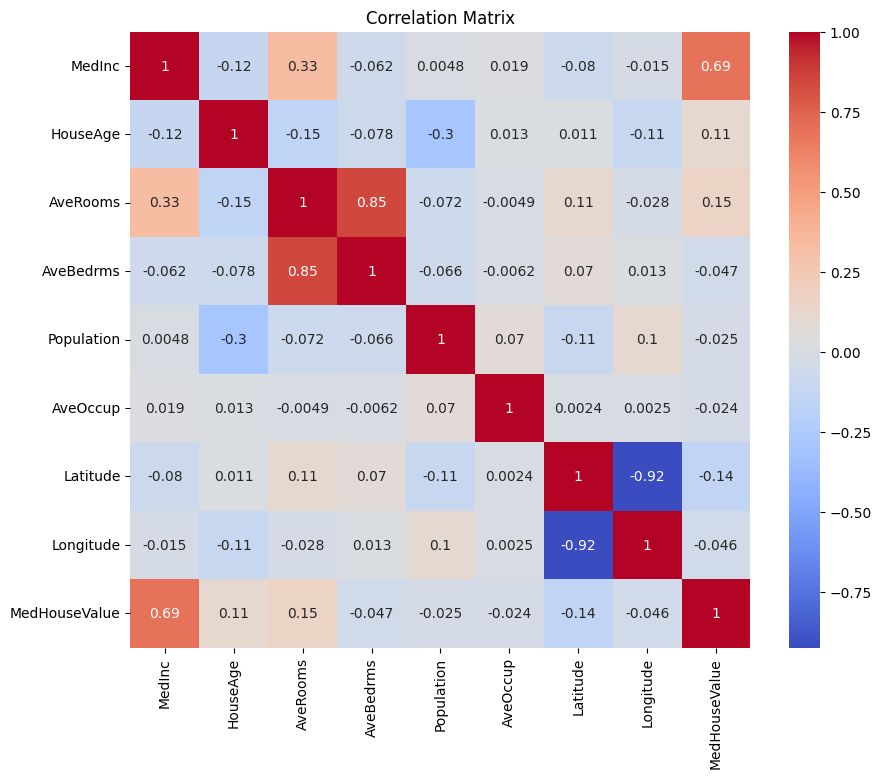
让我们首先创建一个相关矩阵，以了解变量之间的依赖关系。

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

输出：

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

您可以分析上述相关矩阵，为我们的回归模型选择相关和独立变量。相关矩阵提供了数据集中每对变量之间关系的见解。

在给定的相关矩阵中，MedHouseValue是因变量，因为我们正在尝试预测的变量。独立变量与MedHouseValue有显著相关性。

根据相关矩阵，您可以确定以下具有与MedHouseValue显著相关性的独立变量：

  • MedInc：该变量与MedHouseValue有很强的正相关性（0.688075），表明随着收入中位数的增加，房屋中位价值也倾向于增加。
  • AveRooms：该变量与MedHouseValue有适度的正相关性（0.151948），表明每个家庭的平均房间数增加时，房屋中位价值也倾向于增加。
  • AveOccup：此变量与MedHouseValue呈弱负相关(-0.023737)，表明随着每户平均入住率的增加，房屋的中位价值往往会下降，但影响相对较小。

通过选择这些自变量，您可以构建一个回归模型，捕捉这些变量与MedHouseValue之间的关系，从而使我们能够根据收入中位数、房间平均数和入住率的中位数对房屋的中位价值进行预测。

您还可以使用以下代码在Python中绘制相关矩阵：

import seaborn as sns
import matplotlib.pyplot as plt

# 假设'housing_df'是包含数据的DataFrame
# 绘制相关矩阵
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

基于上述内容，您可以简化重点关注一些关键特征，例如MedInc（收入中位数）、AveRooms（每户平均房间数）和AveOccup（每户平均入住率）。

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

上述代码块从housing_df数据框中选择了特定特征进行分析。所选特征为MedInc、AveRooms和AveOccup，它们存储在selected_features列表中。

然后，将数据框housing_df子集化，仅包括这些选定特征，并将结果存储在X列表中。

目标变量MedHouseValue从housing_df中提取，并存储在y列表中。

特征缩放

您将使用标准化来确保所有特征在相同的尺度上，提高模型性能和可比性。

标准化是一种预处理技术，将数值特征按照均值为0、标准差为1进行缩放。这个过程确保所有特征在相同的尺度上，对于对输入特征尺度敏感的机器学习模型至关重要。通过对特征进行标准化，可以通过减少具有较大范围的特征对模型的影响来提高模型性能和可比性。

from sklearn.preprocessing import StandardScaler

# 初始化StandardScaler对象
scaler = StandardScaler()

# 将缩放器与数据拟合并进行转换
X_scaled = scaler.fit_transform(X)

# 打印缩放后的数据
print(X_scaled)

输出：

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

输出代表在应用StandardScaler后特征MedInc、AveRooms和AveOccup的缩放值。这些值现在围绕0为中心，标准差为1，确保所有特征在相同的尺度上。

第一行[ 2.34476576 0.62855945 -0.04959654]表示对于第一个数据点，缩放后的MedInc值为2.34476576，AveRooms为0.62855945，AveOccup为-0.04959654。类似地，第二行[ 2.33223796 0.32704136 -0.09251223]表示第二个数据点的缩放值，依此类推。

经过缩放，数值范围大约从-1.14259331到2.34476576，表明特征现在已经被归一化并且可比。这对于对输入特征的规模敏感的机器学习模型至关重要，因为它可以防止具有大范围的特征主导模型。

实现多元线性回归

现在你已经完成了数据预处理，让我们在Python中实现多元线性回归。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# 初始化'LinearRegression'模型并拟合训练数据。
model = LinearRegression()
model.fit(X_train, y_train)

# 使用模型预测测试集的目标变量。
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

使用train_test_split函数将数据分割为训练集和测试集。这里，80%的数据用于训练，20%用于测试。

使用均方误差和R平方对模型进行评估。均方误差（MSE）衡量误差或偏差的平方的平均值。

R平方（R2）是一个统计量，表示回归模型中一个或多个自变量解释的因变量方差的比例。

输出：

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

上面的输出提供了评估多元线性回归模型性能的两个关键指标：

均方误差（MSE）： 0.7006855912225249
MSE 衡量目标变量的预测值与实际值之间的平均平方差异。较低的MSE表示模型性能更好，因为这意味着模型做出了更准确的预测。在这种情况下，MSE为 0.7006855912225249，表明模型并非完美，但具有合理水平的准确性。通常MSE值应该接近于0，数值越低表示性能越好。

决定系数（R2）： 0.4652924370503557
R2 衡量因变量中可预测的方差比例来自自变量。取值范围在0到1之间，1表示完美预测，0表示无线性关系。在这种情况下，R2值为 0.4652924370503557，表明目标变量中大约46.53%的方差可以通过模型中使用的自变量进行解释。这表明模型能够捕捉变量之间的重要关系部分，但并非全部。

让我们来看一些重要的图表：

# 残差图
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# 预测 vs 实际图
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

使用statsmodels

Python中的Statsmodels库是进行统计分析的强大工具。它提供了广泛的统计模型和测试，包括线性回归、时间序列分析和非参数方法。

在多元线性回归的背景下，statsmodels可以用于对数据拟合线性模型，然后对模型进行各种统计测试和分析。这对于理解自变量和因变量之间的关系以及基于模型进行预测特别有用。

import statsmodels.api as sm

# 将常数项添加到模型
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# 残差的Q-Q图
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

输出：

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

这是上表的总结：

模型总结

该模型是一个普通最小二乘回归模型，属于线性回归模型的一种。因变量是MedHouseValue，该模型的R-squared值为0.485，表示约48.5%的MedHouseValue变异可以由自变量解释。调整后的R-squared值为0.484，是R-squared的一种修改版本，惩罚模型包含额外自变量的情况。

模型拟合度

该模型采用最小二乘法进行拟合，F统计量为5173，表明该模型拟合良好。在假定零假设成立的情况下，观察到至少与观察到的F统计量一样极端的概率约为0。这表明该模型在统计上具有显著性。

模型系数

模型系数如下：

  • 常数项为2.0679，表示当所有自变量为0时，预测的MedHouseValue约为2.0679。
  • x1的系数（在本例中为MedInc）为0.8300，表示MedInc每增加一个单位，预测的MedHouseValue大约增加0.83个单位，假设其他所有自变量保持不变。
  • x2（在本例中为AveRooms）的系数为-0.1000，这意味着每增加一个单位的x2，预测的MedHouseValue将减少约0.10个单位，假设所有其他自变量保持不变。
  • x3（在本例中为AveOccup）的系数为-0.0397，这意味着每增加一个单位的x3，预测的MedHouseValue将减少约0.04个单位，假设所有其他自变量保持不变。

模型诊断

模型诊断如下：

  • Omnibus检验统计量为3981.290，表明残差不服从正态分布。
  • Durbin-Watson统计量为1.983，表明残差中没有显著的自相关性。
  • Jarque-Bera检验统计量为11583.284，表明残差不服从正态分布。
  • 残差的偏度为1.260，表明残差向右偏斜。
  • 残差的峰度为6.239，表明残差是尖峰的（即比正态分布有更高的峰值和更重的尾巴）。
  • 条件数为1.42，表明模型对数据的微小变化不敏感。

处理多重共线性

多重共线性是多元线性回归中常见的问题，指两个或更多自变量之间高度相关。这可能导致回归系数的估计不稳定和不可靠。

要检测和处理多重共线性，可以使用方差膨胀因子。VIF衡量了如果您的预测变量相关，估计回归系数的方差会增加多少。VIF为1意味着给定预测变量与其他预测变量之间没有相关性。超过5或10的VIF值表示存在问题的共线性程度。

在下面的代码块中，让我们计算模型中每个自变量的VIF。如果任何VIF值超过5，应考虑从模型中删除该变量。

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# VIF值的条形图
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

输出：

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

每个特征的VIF值如下：

  • MedInc：VIF值为1.120166，表明与其他自变量几乎没有相关性。这表明MedInc与模型中的其他自变量之间没有高度相关性。
  • AveRooms：VIF值为1.119797，表明与其他自变量几乎没有相关性。这表明AveRooms与模型中的其他自变量之间没有高度相关性。
  • AveOccup：VIF 值为 1.000488，表明与其他自变量没有相关性。这表明AveOccup与模型中的其他自变量没有相关性。

总的来说，这些 VIF 值都低于 5，表明模型中的自变量之间没有显著的多重共线性。这表明模型是稳定可靠的，自变量的系数不会受到多重共线性的显著影响。

交叉验证技术

交叉验证是用于评估机器学习模型性能的技术。它是一种重采样过程，用于评估模型在数据样本有限的情况下的表现。该过程有一个称为k的参数，指的是将给定数据样本分成的组数。因此，该过程通常被称为 k 折交叉验证。

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# 交叉验证分数的线图
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

输出：

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

交叉验证分数显示模型在未见数据上的表现。这些分数的范围从 0.31191043 到 0.51269138，表明模型的性能在不同的折叠中有所变化。更高的分数表示更好的性能。

平均 CV R^2 分数为 0.41864482644003276，这意味着，平均而言，模型解释了目标变量方差的约 41.86%。这是一个中等水平的解释，表明模型在预测目标变量方面有一定效果，但可能还需要进一步改进或完善。

这些分数可用于评估模型的泛化能力，并确定改进的潜在领域。

特征选择方法

递归特征消除方法是一种特征选择技术，它会递归性地消除最不重要的特征，直到达到指定数量的特征为止。当处理大量特征且目标是选择最具信息量特征子集时，此方法特别有用。

在提供的代码中，首先从 sklearn.feature_selection 导入 RFE 类。然后创建一个指定估算器（在本例中为 LinearRegression）的 RFE 实例，并将 n_features_to_select 设置为 2，表示我们要选择前 2 个特征。

接下来，我们将RFE对象适配到我们的标准化特征X_scaled和目标变量y上。RFE对象的support_属性返回一个布尔掩码，指示选择了哪些特征。

为了可视化特征的排名，您可以创建一个包含特征名称及其对应排名的DataFrame。RFE对象的ranking_属性返回每个特征的排名，较低的值表示更重要的特征。然后，您可以绘制一个按排名值排序的特征排名条形图。这个图表有助于我们了解模型中每个特征的相对重要性。

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# 特征排名条形图
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

输出：

Selected Features: [ True  True False]

根据上图，最适合的两个特征是MedInc和AveRooms。这也可以通过上面模型输出的信息进行验证，因为因变量MedHouseValue主要依赖于MedInc和AveRooms。

常见问题解答

如何在Python中实现多元线性回归？

要在Python中实现多元线性回归，您可以使用像statsmodels或scikit-learn这样的库。以下是使用scikit-learn的快速概述：

from sklearn.linear_model import LinearRegression
import numpy as np

# 示例数据
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # 预测变量
y = np.array([5, 7, 9, 11])  # 目标变量

# 创建并拟合模型
model = LinearRegression()
model.fit(X, y)

# 获取系数和截距
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# 进行预测
predictions = model.predict(X)
print("Predictions:", predictions)

这演示了如何拟合模型、获取系数和进行预测。

多元线性回归在Python中的假设是什么？

多元线性回归依赖于几个假设以确保结果有效：

  1. 线性性：预测变量与目标变量之间的关系是线性的。
  2. 独立性：观测值彼此独立。
  3. 同方差性：残差（误差）的方差在所有独立变量的各个水平上都是恒定的。
  4. 残差的正态性：残差呈正态分布。
  5. 无多重共线性: 自变量之间不高度相关。

您可以使用残差图、方差膨胀因子（VIF）或统计检验来测试这些假设。

如何在Python中解释多元回归结果？

回归结果中的关键指标包括：

  1. 系数（coef_）: 表示对应预测变量在其他变量保持不变的情况下，目标变量随其变化的量。

例如：X1的系数为2意味着目标变量在X1每增加1个单位时增加2个单位，其他变量保持不变。

2.截距（intercept_）: 表示当所有预测变量为零时目标变量的预测值。

3.R平方: 解释目标变量方差中被预测变量解释的比例。

例如：R^2为0.85表示模型解释了目标变量变异性的85%。

4.P值（在statsmodels中）: 评估预测变量的统计显著性。通常p值＜0.05表示预测变量具有显著性。

简单线性回归和多元线性回归在Python中有什么区别？

Feature Simple Linear Regression Multiple Linear Regression
自变量个数 一个 多个
模型方程 y = β0 + β1x + ε y = β0 + β1×1 + β2×2 + … + βnxn + ε
假设 与多元线性回归相同，但只有一个自变量 与简单线性回归相同，但对多个自变量有额外的假设
系数解释 目标变量在独立变量单位变化时的变化，同时保持所有其他变量不变（简单线性回归不适用） 目标变量在一个独立变量单位变化时的变化，同时保持所有其他独立变量不变
模型复杂度 较低 较高
模型灵活性 较低 较高
过拟合风险 较低 较高
可解释性 更容易解释 更具挑战性的解释
适用性 适用于简单关系 适用于具有多个因素的复杂关系
示例 基于卧室数量预测房屋价格 基于卧室数量、建筑面积和位置预测房屋价格

结论

在这个全面的教程中，您学会了如何使用加利福尼亚房屋数据集实现多元线性回归。您解决了诸如多重共线性、交叉验证、特征选择和正则化等关键方面，深入理解了每个概念。您还学会了如何使用可视化来说明残差、特征重要性和整体模型性能。您现在可以轻松在Python中构建强大的回归模型，并将这些技能应用于实际问题。

Source:
https://www.digitalocean.com/community/tutorials/multiple-linear-regression-python