Multiple Lineare Regression in Python: Ein umfassender Leitfaden

Einführung

Die multiple lineare Regression ist eine grundlegende statistische Technik, die verwendet wird, um die Beziehung zwischen einer abhängigen Variablen und mehreren unabhängigen Variablen zu modellieren. In Python bieten Tools wie scikit-learn und statsmodels robuste Implementierungen für Regressionsanalysen. Dieses Tutorial führt Sie durch die Implementierung, Interpretation und Auswertung von multiplen linearen Regressionsmodellen mit Python.

Voraussetzungen

Vor dem Einstieg in die Implementierung stellen Sie sicher, dass Sie Folgendes haben:

• Grundlegendes Verständnis von Python. Sie können sich an das Python Tutorial für Anfänger wenden.
• Vertrautheit mit scikit-learn für Aufgaben im Bereich maschinelles Lernen. Sie können sich an das Python scikit-learn Tutorial wenden.
• Verständnis der Datenvisualisierungskonzepte in Python. Sie können sich auf Wie man Daten in Python 3 mit matplotlib darstellt und Datenanalyse und Visualisierung mit pandas und Jupyter Notebook in Python 3 beziehen.
• Python 3.x installiert mit den folgenden Bibliotheken numpy, pandas, matplotlib, seaborn, scikit-learn und statsmodels installiert.

Was ist Multiple Lineare Regression?

Die Multiple Lineare Regression (MLR) ist eine statistische Methode, die die Beziehung zwischen einer abhängigen Variable und zwei oder mehr unabhängigen Variablen modelliert. Sie ist eine Erweiterung der einfachen linearen Regression, die die Beziehung zwischen einer abhängigen Variable und einer einzigen unabhängigen Variable modelliert. Bei MLR wird die Beziehung mit der Formel modelliert:

Wo:

Beispiel: Vorhersage des Preises eines Hauses basierend auf seiner Größe, Anzahl der Schlafzimmer und Lage. In diesem Fall gibt es drei unabhängige Variablen, d.h. Größe, Anzahl der Schlafzimmer und Lage, und eine abhängige Variable, d.h. Preis, die der zu prognostizierende Wert ist.

Annahmen der Multiplen Linearen Regression

Vor der Implementierung der multiplen linearen Regression ist es wichtig sicherzustellen, dass die folgenden Annahmen erfüllt sind:

1. Linearität: Die Beziehung zwischen der abhängigen Variablen und den unabhängigen Variablen ist linear.

2. Unabhängigkeit der Fehler: Residuen (Fehler) sind voneinander unabhängig. Dies wird oft mit dem Durbin-Watson-Test überprüft.

3. Homoskedastizität: Die Varianz der Residuen ist über alle Ebenen der unabhängigen Variablen konstant. Ein Residualplot kann dabei helfen, dies zu überprüfen.

4. Keine Multikollinearität: Unabhängige Variablen sind nicht stark korreliert. Der Varianzinflationsfaktor (VIF) wird häufig verwendet, um Multikollinearität zu erkennen.

5. Normalität der Residuen: Die Residuen sollten einer normalen Verteilung folgen. Dies kann mithilfe eines Q-Q-Plots überprüft werden.

6. Ausreißereinfluss: Ausreißer oder hoch leveragierte Punkte sollten das Modell nicht überproportional beeinflussen.

Diese Annahmen stellen sicher, dass das Regressionsmodell gültig ist und die Ergebnisse zuverlässig sind. Das Nichterfüllen dieser Annahmen kann zu verfälschten oder irreführenden Ergebnissen führen.

Daten vorverarbeiten

In diesem Abschnitt lernen Sie, wie Sie das Multiple-Linear-Regressionsmodell in Python verwenden, um Hauspreise basierend auf Merkmalen aus dem California Housing Dataset vorherzusagen. Sie werden lernen, wie man Daten vorverarbeitet, ein Regressionsmodell anpasst und seine Leistung bewertet, während man auf häufige Herausforderungen wie Multikollinearität, Ausreißer und Merkmalsauswahl eingeht.

Schritt 1 – Laden Sie das Dataset

Sie werden das California Housing Dataset verwenden, ein beliebtes Dataset für Regressionsaufgaben. Dieses Dataset enthält 13 Merkmale über Häuser in den Vororten von Boston und deren entsprechenden Medianhauspreis.

Zuerst installieren wir die notwendigen Pakete:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # Importieren Sie die fetch_california_housing Funktion aus sklearn.datasets, um den Datensatz zum kalifornischen Wohnungsbestand zu laden.
import pandas as pd  # Importieren Sie pandas für die Datenmanipulation und -analyse.
import numpy as np  # Importieren Sie numpy für numerische Berechnungen.

# Laden Sie den Datensatz zum kalifornischen Wohnungsbestand mithilfe der fetch_california_housing Funktion.
housing = fetch_california_housing()

# Konvertieren Sie die Daten des Datensatzes in ein pandas DataFrame, wobei die Merkmalsnamen als Spaltenüberschriften verwendet werden.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# Fügen Sie das Zielvariable 'MedHouseValue' zum DataFrame hinzu, unter Verwendung der Zielwerte des Datensatzes.
housing_df['MedHouseValue'] = housing.target

# Zeigen Sie die ersten Zeilen des DataFrames an, um einen Überblick über den Datensatz zu erhalten.
print(housing_df.head())

Sie sollten die folgende Ausgabe des Datensatzes beobachten:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

Hier ist, was jeder der Attribute bedeutet:

Schritt 2 – Daten vorverarbeiten

Überprüfen auf fehlende Werte

Stellt sicher, dass im Datensatz keine fehlenden Werte vorhanden sind, die die Analyse beeinträchtigen könnten.

print(housing_df.isnull().sum())

Ausgabe:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

Feature-Auswahl

Lassen Sie uns zunächst eine Korrelationsmatrix erstellen, um die Abhängigkeiten zwischen den Variablen zu verstehen.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

Ausgabe:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

Sie können die obige Korrelationsmatrix analysieren, um die abhängigen und unabhängigen Variablen für unser Regressionsmodell auszuwählen. Die Korrelationsmatrix liefert Einblicke in die Beziehungen zwischen jedem Variablenpaar im Datensatz.

In der gegebenen Korrelationsmatrix ist MedHouseValue die abhängige Variable, da es die Variable ist, die wir zu prognostizieren versuchen. Die unabhängigen Variablen korrelieren signifikant mit MedHouseValue.

Basierend auf der Korrelationsmatrix können Sie die folgenden unabhängigen Variablen identifizieren, die eine signifikante Korrelation mit MedHouseValue aufweisen:

• MedInc: Diese Variable hat eine starke positive Korrelation (0,688075) mit MedHouseValue, was darauf hindeutet, dass mit steigendem Median-Einkommen auch der Median-Hauswert tendenziell steigt.
• AveRooms: Diese Variable hat eine mäßige positive Korrelation (0,151948) mit MedHouseValue, was darauf hindeutet, dass mit zunehmender durchschnittlicher Anzahl von Zimmern pro Haushalt auch der Median-Hauswert tendenziell steigt.
• AveOccup: Diese Variable hat eine schwache negative Korrelation (-0.023737) mit MedHouseValue, was darauf hindeutet, dass mit zunehmender durchschnittlicher Belegung pro Haushalt der mittlere Hauswert tendenziell abnimmt, der Effekt jedoch relativ gering ist.

Indem Sie diese unabhängigen Variablen auswählen, können Sie ein Regressionsmodell erstellen, das die Beziehungen zwischen diesen Variablen und MedHouseValue erfasst, um Vorhersagen über den mittleren Hauswert basierend auf dem mittleren Einkommen, der durchschnittlichen Anzahl von Zimmern und der durchschnittlichen Belegung zu treffen.

Sie können die Korrelationsmatrix auch in Python mit dem folgenden Code plotten:

import seaborn as sns
import matplotlib.pyplot as plt

# Angenommen 'housing_df' ist der DataFrame, der die Daten enthält
# Plotten der Korrelationsmatrix
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

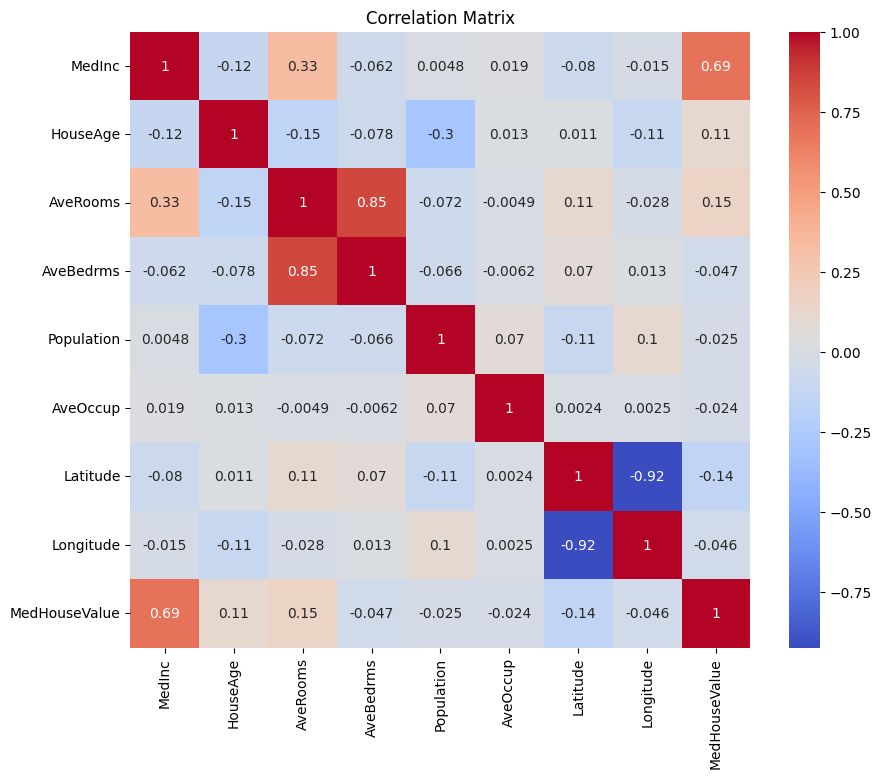
Sie werden sich zur Vereinfachung auf einige wichtige Merkmale konzentrieren, wie z.B. MedInc (mittleres Einkommen), AveRooms (durchschnittliche Zimmer pro Haushalt) und AveOccup (durchschnittliche Belegung pro Haushalt), basierend auf dem oben Genannten.

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

Der obige Codeblock wählt spezifische Merkmale aus dem housing_df-Datenrahmen für die Analyse aus. Die ausgewählten Merkmale sind MedInc, AveRooms und AveOccup, die in der Liste selected_features gespeichert sind.

Der Datenrahmen housing_df wird dann so unterteilt, dass nur diese ausgewählten Merkmale enthalten sind, und das Ergebnis wird in der Liste X gespeichert.

Die Zielvariable MedHouseValue wird aus housing_df extrahiert und in der Liste y gespeichert.

Skalierung der Merkmale

Sie werden die Standardisierung verwenden, um sicherzustellen, dass alle Merkmale auf der gleichen Skala liegen, was die Leistung und Vergleichbarkeit des Modells verbessert.

Die Standardisierung ist eine Vorverarbeitungstechnik, die numerische Merkmale so skaliert, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 haben. Dieser Prozess stellt sicher, dass alle Merkmale auf derselben Skala liegen, was für Machine-Learning-Modelle, die empfindlich auf die Skala der Eingabemerkmale reagieren, unerlässlich ist. Durch die Standardisierung der Merkmale können Sie die Leistung und Vergleichbarkeit des Modells verbessern, indem Sie den Einfluss von Merkmalen mit großen Bereichen reduzieren, die das Modell dominieren.

from sklearn.preprocessing import StandardScaler

# Initialisieren des StandardScaler-Objekts
scaler = StandardScaler()

# Passen Sie den Scaler an die Daten an und transformieren Sie sie
X_scaled = scaler.fit_transform(X)

# Skalierte Daten ausgeben
print(X_scaled)

Ergebnis:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

Die Ausgabe repräsentiert die skalierten Werte der Merkmale MedInc, AveRooms und AveOccup nach Anwendung des StandardScaler. Die Werte sind nun um 0 zentriert und haben eine Standardabweichung von 1, was sicherstellt, dass alle Merkmale auf derselben Skala liegen.

Die erste Zeile [ 2.34476576 0.62855945 -0.04959654] zeigt, dass für den ersten Datenpunkt der skalierte Wert von MedInc 2,34476576 beträgt, AveRooms 0,62855945 und AveOccup -0,04959654 ist. Ebenso repräsentiert die zweite Zeile [ 2.33223796 0.32704136 -0.09251223] die skalierten Werte für den zweiten Datenpunkt und so weiter.

Die skalierten Werte reichen von ungefähr -1,14259331 bis 2,34476576, was darauf hindeutet, dass die Merkmale nun normalisiert und vergleichbar sind. Dies ist für Machine-Learning-Modelle, die empfindlich auf den Maßstab der Eingabemerkmale reagieren, unerlässlich, da verhindert wird, dass Merkmale mit großen Spannen das Modell dominieren.

Implementieren Sie Multiple Lineare Regression

Nachdem Sie mit der Datenverarbeitung fertig sind, implementieren wir jetzt multiple lineare Regression in Python.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# Das Modell 'LinearRegression' wird initialisiert und an die Trainingsdaten angepasst.
model = LinearRegression()
model.fit(X_train, y_train)

# Das Modell wird verwendet, um die Zielvariable für den Testdatensatz vorherzusagen.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

Die Funktion train_test_split wird verwendet, um die Daten in Trainings- und Testsets aufzuteilen. Hier werden 80 % der Daten für das Training und 20 % für Tests verwendet.

Das Modell wird anhand des Mean Squared Error und des R-Quadrats evaluiert. Der Mean Squared Error (MSE) misst den Durchschnitt der Quadrate der Fehler oder Abweichungen.

Das R-Quadrat (R2) ist ein statistisches Maß, das den Anteil der Varianz für eine abhängige Variable darstellt, der durch eine unabhängige Variable oder Variablen in einem Regressionsmodell erklärt wird.

Ausgabe:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

Die obige Ausgabe liefert zwei wichtige Metriken zur Bewertung der Leistung des Modells der multiplen linearen Regression:

Mittlerer quadratischer Fehler (MSE): 0.7006855912225249
Der MSE misst die durchschnittliche quadrierte Differenz zwischen den vorhergesagten und tatsächlichen Werten der Zielvariablen. Ein niedriger MSE deutet auf eine bessere Modellleistung hin, da dies bedeutet, dass das Modell genauere Vorhersagen trifft. In diesem Fall beträgt der MSE 0.7006855912225249, was darauf hindeutet, dass das Modell nicht perfekt ist, aber ein vernünftiges Maß an Genauigkeit aufweist. Die MSE-Werte sollten in der Regel näher an 0 liegen, wobei niedrigere Werte eine bessere Leistung anzeigen.

Bestimmtheitsmaß (R2): 0.4652924370503557
R2 misst den Anteil der Varianz in der abhängigen Variablen, der aus den unabhängigen Variablen vorhergesagt werden kann. Es reicht von 0 bis 1, wobei 1 eine perfekte Vorhersage und 0 keine lineare Beziehung angibt. In diesem Fall beträgt der R2-Wert 0.4652924370503557, was darauf hindeutet, dass etwa 46,53% der Varianz in der Zielvariablen durch die im Modell verwendeten unabhängigen Variablen erklärt werden können. Dies legt nahe, dass das Modell einen signifikanten Teil der Beziehungen zwischen den Variablen erfassen kann, aber nicht alle.

Werfen wir einen Blick auf einige wichtige Diagramme:

# Residuenplot
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# Vorhergesagtes vs. Tatsächliches Diagramm
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

Verwendung von statsmodels

Die Statsmodels-Bibliothek in Python ist ein leistungsstolles Werkzeug für statistische Analysen. Sie bietet eine Vielzahl von statistischen Modellen und Tests, einschließlich linearer Regression, Zeitreihenanalyse und nichtparametrischer Methoden.

Im Kontext der multiplen linearen Regression kann statsmodels verwendet werden, um ein lineares Modell an die Daten anzupassen und dann verschiedene statistische Tests und Analysen am Modell durchzuführen. Dies kann besonders nützlich sein, um die Beziehungen zwischen den unabhängigen und abhängigen Variablen zu verstehen und Vorhersagen auf Basis des Modells zu treffen.

import statsmodels.api as sm

# Füge dem Modell eine Konstante hinzu
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# Q-Q Plot für Residuen
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

Ausgabe:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

Hier ist die Zusammenfassung der obigen Tabelle:

Modellzusammenfassung

Das Modell ist ein Ordinary Least Squares Regressionsmodell, das eine Art von linearem Regressionsmodell darstellt. Die abhängige Variable ist MedHouseValue und das Modell hat einen R-Quadrat-Wert von 0,485, was darauf hindeutet, dass etwa 48,5 % der Variation in MedHouseValue durch die unabhängigen Variablen erklärt werden können. Der angepasste R-Quadrat-Wert beträgt 0,484, was eine modifizierte Version des R-Quadrats ist, die das Modell bestraft, wenn zusätzliche unabhängige Variablen aufgenommen werden.

Modellanpassung

Das Modell wurde mit der Methode der kleinsten Quadrate angepasst, und die F-Statistik beträgt 5173, was darauf hinweist, dass das Modell gut passt. Die Wahrscheinlichkeit, eine F-Statistik zu beobachten, die mindestens so extrem ist wie die beobachtete, unter der Annahme, dass die Nullhypothese wahr ist, beträgt ungefähr 0. Dies deutet darauf hin, dass das Modell statistisch signifikant ist.

Modellkoeffizienten

Die Modellkoeffizienten sind wie folgt:

• Der konstante Term beträgt 2,0679, was bedeutet, dass der vorhergesagte MedHouseValue ungefähr 2,0679 beträgt, wenn alle unabhängigen Variablen 0 sind.
• Der Koeffizient für x1 (in diesem Fall MedInc) beträgt 0,8300, was bedeutet, dass bei jedem Anstieg von einer Einheit in MedInc der vorhergesagte MedHouseValue um ungefähr 0,83 Einheiten steigt, vorausgesetzt, alle anderen unabhängigen Variablen bleiben konstant.
• Der Koeffizient für x2 (in diesem Fall AveRooms) beträgt -0.1000, was darauf hinweist, dass bei jeder Einheitserhöhung von x2 der vorhergesagte Wert von MedHouseValue um etwa 0,10 Einheiten sinkt, unter der Annahme, dass alle anderen unabhängigen Variablen konstant gehalten werden.
• Der Koeffizient für x3 (in diesem Fall AveOccup) beträgt -0.0397, was darauf hinweist, dass bei jeder Einheitserhöhung von x3 der vorhergesagte Wert von MedHouseValue um etwa 0,04 Einheiten sinkt, unter der Annahme, dass alle anderen unabhängigen Variablen konstant gehalten werden.

Modell-Diagnostik

Die Modell-Diagnostik erfolgt wie folgt:

• Der Omnibus-Teststatistik beträgt 3981.290, was darauf hinweist, dass die Residuen nicht normal verteilt sind.
• Die Durbin-Watson-Statistik beträgt 1.983, was darauf hinweist, dass keine signifikante Autokorrelation in den Residuen vorhanden ist.
• Der Jarque-Bera-Teststatistik beträgt 11583.284, was darauf hinweist, dass die Residuen nicht normal verteilt sind.
• Die Schiefe der Residuen beträgt 1.260, was darauf hinweist, dass die Residuen nach rechts geneigt sind.
• Die Kurtosis der Residuen beträgt 6.239, was darauf hinweist, dass die Residuen leptokurtisch sind (d.h. sie haben einen höheren Peak und schwerere Schwänze als eine Normalverteilung).
• Die Konditionszahl beträgt 1,42, was darauf hinweist, dass das Modell nicht empfindlich auf kleine Änderungen in den Daten reagiert.

Umgang mit Multikollinearität

Multikollinearität ist ein häufiges Problem bei der multiplen linearen Regression, bei dem zwei oder mehr unabhängige Variablen stark miteinander korreliert sind. Dies kann zu instabilen und unzuverlässigen Schätzungen der Koeffizienten führen.

Um Multikollinearität zu erkennen und zu behandeln, können Sie den Varianzinflationsfaktor verwenden. Der VIF misst, wie sehr die Varianz eines geschätzten Regressionskoeffizienten ansteigt, wenn Ihre Prädiktoren korreliert sind. Ein VIF von 1 bedeutet, dass es keine Korrelation zwischen einem bestimmten Prädiktor und den anderen Prädiktoren gibt. VIF-Werte über 5 oder 10 deuten auf eine problematische Menge an Kollinearität hin.

Im folgenden Code-Block berechnen wir den VIF für jede unabhängige Variable in unserem Modell. Wenn ein VIF-Wert über 5 liegt, sollten Sie erwägen, die Variable aus dem Modell zu entfernen.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# Balkendiagramm für VIF-Werte
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

Ausgabe:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

Die VIF-Werte für jedes Merkmal sind wie folgt:

• MedInc: Der VIF-Wert beträgt 1,120166, was auf eine sehr geringe Korrelation mit anderen unabhängigen Variablen hinweist. Dies legt nahe, dass MedInc nicht stark mit anderen unabhängigen Variablen im Modell korreliert ist.
• AveRooms: Der VIF-Wert beträgt 1,119797, was auf eine sehr geringe Korrelation mit anderen unabhängigen Variablen hinweist. Dies legt nahe, dass AveRooms nicht stark mit anderen unabhängigen Variablen im Modell korreliert ist.
• AveOccup: Der VIF-Wert beträgt 1,000488, was darauf hinweist, dass keine Korrelation mit anderen unabhängigen Variablen besteht. Dies legt nahe, dass AveOccup nicht mit anderen unabhängigen Variablen im Modell korreliert ist.

Im Allgemeinen liegen diese VIF-Werte alle unter 5, was darauf hindeutet, dass keine signifikante Multikollinearität zwischen den unabhängigen Variablen im Modell besteht. Dies legt nahe, dass das Modell stabil und zuverlässig ist und dass die Koeffizienten der unabhängigen Variablen nicht signifikant von der Multikollinearität beeinflusst werden.

Kreuzvalidierungstechniken

Kreuzvalidierung ist eine Technik, die zur Bewertung der Leistung eines maschinellen Lernmodells verwendet wird. Es handelt sich um ein Resampling-Verfahren, um ein Modell zu bewerten, wenn wir eine begrenzte Datenprobe haben. Das Verfahren hat einen einzelnen Parameter namens k, der sich auf die Anzahl der Gruppen bezieht, in die eine bestimmte Datenprobe aufgeteilt werden soll. Als solches wird das Verfahren oft als k-fache Kreuzvalidierung bezeichnet.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# Liniendiagramm für Kreuzvalidierungswerte
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

Ausgabe:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

Die Kreuzvalidierungswerte geben an, wie gut das Modell auf nicht gesehenen Daten funktioniert. Die Werte reichen von 0,31191043 bis 0,51269138, was darauf hinweist, dass die Leistung des Modells je nach verschiedenen Falten variiert. Ein höherer Wert deutet auf eine bessere Leistung hin.

Der durchschnittliche CV R^2-Score beträgt 0,41864482644003276, was darauf hindeutet, dass das Modell im Durchschnitt etwa 41,86% der Varianz der Zielvariable erklärt. Dies ist ein moderates Erklärungsniveau, das darauf hinweist, dass das Modell in gewissem Maße effektiv ist, um die Zielvariable vorherzusagen, aber von weiteren Verbesserungen oder Verfeinerungen profitieren könnte.

Diese Werte können verwendet werden, um die Generalisierbarkeit des Modells zu bewerten und potenzielle Verbesserungsbereiche zu identifizieren.

Feature-Auswahlmethoden

Die Methode der rekursiven Merkmalseliminierung ist eine Feature-Auswahltechnik, die rekursiv die am wenigsten wichtigen Merkmale eliminiert, bis eine bestimmte Anzahl von Merkmalen erreicht ist. Diese Methode ist besonders nützlich, wenn es um eine große Anzahl von Merkmalen geht und das Ziel darin besteht, eine Teilmenge der informativsten Merkmale auszuwählen.

Im bereitgestellten Code importieren Sie zunächst die Klasse RFE aus sklearn.feature_selection. Erstellen Sie dann eine Instanz von RFE mit einem spezifizierten Schätzer (in diesem Fall LinearRegression) und setzen Sie n_features_to_select auf 2, was darauf hindeutet, dass wir die besten 2 Merkmale auswählen möchten.

Als nächstes passen wir das RFE-Objekt an unsere skalierten Features X_skaliert und die Zielvariable y an. Das Attribut support_ des RFE-Objekts gibt eine boolesche Maske zurück, die anzeigt, welche Features ausgewählt wurden.

Um das Ranking der Features zu visualisieren, erstellen Sie ein DataFrame mit den Feature-Namen und ihren entsprechenden Rankings. Das Attribut ranking_ des RFE-Objekts gibt das Ranking jedes Features zurück, wobei niedrigere Werte auf wichtigere Features hinweisen. Anschließend erstellen Sie ein Balkendiagramm der Feature-Rankings, sortiert nach ihren Ranking-Werten. Dieses Diagramm hilft uns zu verstehen, wie wichtig jedes Feature im Modell ist.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# Balkendiagramm der Feature-Rankings
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

Ausgabe:

Selected Features: [ True  True False]

Basierend auf dem obigen Diagramm sind die 2 am besten geeigneten Features MedInc und AveRooms. Dies kann auch durch die Ausgabe des Modells oben bestätigt werden, da die abhängige Variable MedHouseValue hauptsächlich von MedInc und AveRooms abhängt.

FAQs

Wie implementiert man die multiple lineare Regression in Python?

Um eine multiple lineare Regression in Python zu implementieren, können Sie Bibliotheken wie statsmodels oder scikit-learn verwenden. Hier ist eine kurze Übersicht zur Verwendung von scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# Beispiel Daten
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # Prädiktorvariablen
y = np.array([5, 7, 9, 11])  # Zielvariable

# Modell erstellen und anpassen
model = LinearRegression()
model.fit(X, y)

# Koeffizienten und Intercept abrufen
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# Vorhersagen treffen
predictions = model.predict(X)
print("Predictions:", predictions)

Dies zeigt, wie man das Modell anpasst, die Koeffizienten erhält und Vorhersagen trifft.

Was sind die Annahmen der multiplen linearen Regression in Python?

Die multiple lineare Regression stützt sich auf mehrere Annahmen, um gültige Ergebnisse sicherzustellen:

1. Linearität: Die Beziehung zwischen Prädiktoren und der Zielvariablen ist linear.
2. Unabhängigkeit: Beobachtungen sind voneinander unabhängig.
3. Homoskedastizität: Die Varianz der Residuen (Fehler) ist konstant über alle Ebenen der unabhängigen Variablen.
4. Normalverteilung der Residuen: Die Residuen sind normalverteilt.
5. Keine Multikollinearität: Unabhängige Variablen korrelieren nicht stark miteinander.

Sie können diese Annahmen mithilfe von Tools wie Restplots, Variance Inflation Factor (VIF) oder statistischen Tests überprüfen.

Wie interpretiert man Mehrfachregressions-Ergebnisse in Python?

Wichtige Kennzahlen aus den Regressions-Ergebnissen sind:

1. Koeffizienten (coef_): Zeigen die Veränderung der Zielvariablen für eine Einheit Veränderung im entsprechenden Prädiktor, unter Beibehaltung der anderen Variablen konstant.

Beispiel: Ein Koeffizient von 2 für X1 bedeutet, dass die Zielvariable um 2 für jede 1-Einheitserhöhung in X1 ansteigt, unter Beibehaltung der anderen Variablen konstant.

2.Abschnitt (intercept_): Stellt den vorhergesagten Wert der Zielvariablen dar, wenn alle Prädiktoren null sind.

3.R-Quadrat: Erklärt den Anteil der Varianz in der Zielvariablen, der durch die Prädiktoren erklärt wird.

Beispiel: Ein R^2 von 0,85 bedeutet, dass 85% der Variabilität in der Zielvariablen durch das Modell erklärt wird.

4.P-Werte (in statsmodels): Beurteilen die statistische Signifikanz der Prädiktoren. Ein p-Wert < 0,05 deutet in der Regel darauf hin, dass ein Prädiktor signifikant ist.

Was ist der Unterschied zwischen einfacher und multipler linearer Regression in Python?

Schlussfolgerung

In diesem umfassenden Tutorial haben Sie gelernt, Multiple Lineare Regression mithilfe des California Housing Dataset umzusetzen. Sie haben wichtige Aspekte wie Multikollinearität, Kreuzvalidierung, Merkmalsauswahl und Regularisierung behandelt und ein gründliches Verständnis jedes Konzepts vermittelt. Sie haben auch gelernt, Visualisierungen einzubeziehen, um Residuen, Merkmalswichtigkeit und die Gesamtmodellleistung zu veranschaulichen. Sie können nun problemlos robuste Regressionsmodelle in Python erstellen und diese Fähigkeiten auf reale Probleme anwenden.