Regresión Lineal Múltiple en Python: Una Guía Completa

Introducción

La Regresión Lineal Múltiple es una técnica estadística fundamental utilizada para modelar la relación entre una variable dependiente y múltiples variables independientes. En Python, herramientas como scikit-learn y statsmodels proporcionan implementaciones robustas para el análisis de regresión. Este tutorial te guiará a través de la implementación, interpretación y evaluación de modelos de regresión lineal múltiple utilizando Python.

Prerrequisitos

Antes de adentrarte en la implementación, asegúrate de tener lo siguiente:

• Comprensión básica de Python. Puedes consultar el Tutorial de Python para Principiantes.
• Familiaridad con scikit-learn para tareas de aprendizaje automático. Puedes consultar el Tutorial de scikit-learn en Python.
• Comprensión de los conceptos de visualización de datos en Python. Puede hacer referencia a Cómo trazar datos en Python 3 utilizando matplotlib y Análisis y visualización de datos con pandas y Jupyter Notebook en Python 3.
• Python 3.x instalado con las siguientes librerías numpy, pandas, matplotlib, seaborn, scikit-learn y statsmodels instaladas.

¿Qué es la Regresión Lineal Múltiple?

La Regresión Lineal Múltiple (MLR) es un método estadístico que modela la relación entre una variable dependiente y dos o más variables independientes. Es una extensión de la regresión lineal simple, que modela la relación entre una variable dependiente y una sola variable independiente. En MLR, la relación se modela utilizando la fórmula:

Dónde:

Ejemplo: Predicción del precio de una casa basada en su tamaño, número de habitaciones y ubicación. En este caso, hay tres variables independientes, es decir, tamaño, número de habitaciones y ubicación, y una variable dependiente, es decir, precio, que es el valor a predecir.

Supuestos de la Regresión Lineal Múltiple

Antes de implementar la regresión lineal múltiple, es esencial asegurarse de que se cumplan los siguientes supuestos:

1. Linealidad: La relación entre la variable dependiente y las variables independientes es lineal.

2. Independencia de Errores: Los residuos (errores) son independientes entre sí. Esto se suele verificar utilizando la prueba de Durbin-Watson.

3. Homocedasticidad: La varianza de los residuos es constante en todos los niveles de las variables independientes. Un gráfico de residuos puede ayudar a verificar esto.

4. Sin multicolinealidad: Las variables independientes no están altamente correlacionadas. El Factor de Inflación de la Varianza (VIF) se utiliza comúnmente para detectar la multicolinealidad.

5. Normalidad de los residuos: Los residuos deben seguir una distribución normal. Esto se puede verificar utilizando un gráfico Q-Q.

6. Influencia de valores atípicos: Los valores atípicos o puntos de alto apalancamiento no deben influir desproporcionadamente en el modelo.

Estas suposiciones garantizan que el modelo de regresión sea válido y que los resultados sean fiables. No cumplir con estas suposiciones puede llevar a resultados sesgados o engañosos.

Preprocesar los Datos

En esta sección, aprenderás a utilizar el modelo de Regresión Lineal Múltiple en Python para predecir los precios de las casas basándote en características del Conjunto de Datos de Viviendas de California. Aprenderás cómo preprocesar los datos, ajustar un modelo de regresión y evaluar su rendimiento, abordando desafíos comunes como la multicolinealidad, los valores atípicos y la selección de características.

Paso 1 – Cargar el Conjunto de Datos

Utilizarás el Conjunto de Datos de Viviendas de California, un conjunto de datos popular para tareas de regresión. Este conjunto de datos contiene 13 características sobre casas en los suburbios de Boston y su precio mediano correspondiente.

Primero, vamos a instalar los paquetes necesarios:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # Importa la función fetch_california_housing de sklearn.datasets para cargar el conjunto de datos de viviendas de California.
import pandas as pd  # Importa pandas para la manipulación y análisis de datos.
import numpy as np  # Importa numpy para computación numérica.

# Carga el conjunto de datos de viviendas de California usando la función fetch_california_housing.
housing = fetch_california_housing()

# Convierte los datos del conjunto de datos en un DataFrame de pandas, utilizando los nombres de las características como encabezados de columna.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# Agrega la variable objetivo 'MedHouseValue' al DataFrame, utilizando los valores objetivo del conjunto de datos.
housing_df['MedHouseValue'] = housing.target

# Muestra las primeras filas del DataFrame para tener una visión general del conjunto de datos.
print(housing_df.head())

Deberías observar la siguiente salida del conjunto de datos:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

Esto es lo que significa cada uno de los atributos:

Paso 2 – Preprocesar los Datos

Verificar Valores Faltantes

Asegura que no haya valores faltantes en el conjunto de datos que puedan afectar el análisis.

print(housing_df.isnull().sum())

Salida:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

Selección de Características

Primero creemos una matriz de correlación para entender las dependencias entre las variables.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

Salida:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

Puedes analizar la matriz de correlación anterior para seleccionar las variables dependientes e independientes para nuestro modelo de regresión. La matriz de correlación proporciona información sobre las relaciones entre cada par de variables en el conjunto de datos.

En la matriz de correlación dada, MedHouseValue es la variable dependiente, ya que es la variable que intentamos predecir. Las variables independientes tienen una correlación significativa con MedHouseValue.

Basándonos en la matriz de correlación, puedes identificar las siguientes variables independientes que tienen una correlación significativa con MedHouseValue:

• MedInc: Esta variable tiene una correlación positiva fuerte (0.688075) con MedHouseValue, lo que indica que a medida que aumenta el ingreso medio, el valor medio de la casa también tiende a aumentar.
• AveRooms: Esta variable tiene una correlación positiva moderada (0.151948) con MedHouseValue, lo que sugiere que a medida que aumenta el número promedio de habitaciones por hogar, el valor medio de la casa también tiende a aumentar.
• AveOccup: Esta variable tiene una correlación negativa débil (-0.023737) con MedHouseValue, lo que indica que a medida que aumenta la ocupación promedio por hogar, el valor medio de la casa tiende a disminuir, pero el efecto es relativamente pequeño.

Al seleccionar estas variables independientes, puedes construir un modelo de regresión que capture las relaciones entre estas variables y MedHouseValue, lo que nos permite hacer predicciones sobre el valor medio de la casa basadas en el ingreso medio, el número promedio de habitaciones y la ocupación promedio.

También puedes trazar la matriz de correlación en Python utilizando lo siguiente:

import seaborn as sns
import matplotlib.pyplot as plt

# Suponiendo que 'housing_df' es el DataFrame que contiene los datos
# Trazando la matriz de correlación
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

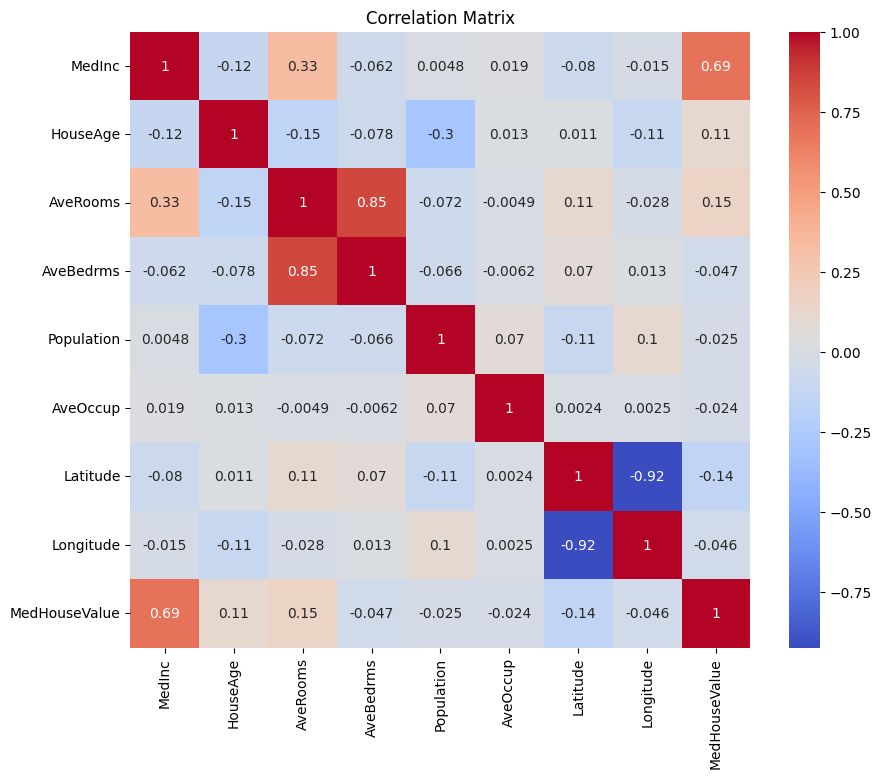
Te enfocarás en algunas características clave para simplificar según lo anterior, como MedInc (ingreso medio), AveRooms (promedio de habitaciones por hogar) y AveOccup (ocupación promedio por hogar).

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

El bloque de código anterior selecciona características específicas del marco de datos housing_df para el análisis. Las características seleccionadas son MedInc, AveRooms y AveOccup, que se almacenan en la lista selected_features.

El DataFrame housing_df luego se subconjunta para incluir solo estas características seleccionadas y el resultado se almacena en la lista X.

La variable objetivo MedHouseValue se extrae de housing_df y se almacena en la lista y.

Escalando características

Utilizarás la Estandarización para asegurar que todas las características estén en la misma escala, mejorando el rendimiento y la comparabilidad del modelo.

La estandarización es una técnica de preprocesamiento que escala las características numéricas para tener una media de 0 y una desviación estándar de 1. Este proceso asegura que todas las características estén en la misma escala, lo cual es esencial para los modelos de aprendizaje automático sensibles a la escala de las características de entrada. Al estandarizar las características, puedes mejorar el rendimiento y la comparabilidad del modelo al reducir el efecto de características con rangos grandes que dominan el modelo.

from sklearn.preprocessing import StandardScaler

# Inicializar el objeto StandardScaler
scaler = StandardScaler()

# Ajustar el scaler a los datos y transformarlos
X_scaled = scaler.fit_transform(X)

# Imprimir los datos escalados
print(X_scaled)

Salida:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

La salida representa los valores escalados de las características MedInc, AveRooms y AveOccup después de aplicar el StandardScaler. Los valores ahora están centrados alrededor de 0 con una desviación estándar de 1, asegurando que todas las características estén en la misma escala.

La primera fila [ 2.34476576 0.62855945 -0.04959654] indica que para el primer punto de datos, el valor escalado de MedInc es 2.34476576, AveRooms es 0.62855945 y AveOccup es -0.04959654. De manera similar, la segunda fila [ 2.33223796 0.32704136 -0.09251223] representa los valores escalados para el segundo punto de datos, y así sucesivamente.

Los valores escalados van aproximadamente desde -1.14259331 hasta 2.34476576, lo que indica que las características ahora están normalizadas y comparables. Esto es esencial para los modelos de aprendizaje automático que son sensibles a la escala de las características de entrada, ya que evita que las características con rangos grandes dominen el modelo.

Implementar Regresión Lineal Múltiple

Ahora que has terminado con el preprocesamiento de datos, implementemos la regresión lineal múltiple en Python.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# Se inicializa el modelo 'LinearRegression' y se ajusta a los datos de entrenamiento.
model = LinearRegression()
model.fit(X_train, y_train)

# Se utiliza el modelo para predecir la variable objetivo para el conjunto de pruebas.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

La función train_test_split se utiliza para dividir los datos en conjuntos de entrenamiento y prueba. Aquí, se usa el 80% de los datos para el entrenamiento y el 20% para las pruebas.

El modelo se evalúa utilizando el Error Cuadrático Medio y R-cuadrado. El Error Cuadrático Medio (MSE) mide el promedio de los cuadrados de los errores o desviaciones.

R-cuadrado (R2) es una medida estadística que representa la proporción de la varianza de una variable dependiente explicada por una variable o variables independientes en un modelo de regresión.

Salida:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

La salida anterior proporciona dos métricas clave para evaluar el rendimiento del modelo de regresión lineal múltiple:

Error cuadrático medio (MSE): 0.7006855912225249
El MSE mide la diferencia cuadrada promedio entre los valores predichos y reales de la variable objetivo. Un MSE más bajo indica un mejor rendimiento del modelo, ya que significa que el modelo está haciendo predicciones más precisas. En este caso, el MSE es 0.7006855912225249, lo que indica que el modelo no es perfecto pero tiene un nivel razonable de precisión. Los valores de MSE suelen estar más cerca de 0, con valores más bajos indicando un mejor rendimiento.

R-cuadrado (R2): 0.4652924370503557
R-cuadrado mide la proporción de la varianza en la variable dependiente que es predecible a partir de las variables independientes. Varía de 0 a 1, donde 1 es una predicción perfecta y 0 indica que no hay relación lineal. En este caso, el valor de R-cuadrado es 0.4652924370503557, lo que indica que aproximadamente el 46.53% de la varianza en la variable objetivo se puede explicar por las variables independientes utilizadas en el modelo. Esto sugiere que el modelo es capaz de capturar una parte significativa de las relaciones entre las variables pero no todas.

¡Veamos algunos gráficos importantes!

# Gráfico de residuos
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# Gráfico de predicción vs real
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

Usando statsmodels

La biblioteca Statsmodels en Python es una herramienta poderosa para análisis estadístico. Proporciona una amplia gama de modelos y pruebas estadísticas, incluyendo regresión lineal, análisis de series temporales y métodos no paramétricos.

En el contexto de la regresión lineal múltiple, statsmodels se puede utilizar para ajustar un modelo lineal a los datos, y luego realizar diversas pruebas y análisis estadísticos en el modelo. Esto puede ser particularmente útil para comprender las relaciones entre las variables independientes y dependientes, y para hacer predicciones basadas en el modelo.

import statsmodels.api as sm

# Agregar una constante al modelo
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# Gráfico Q-Q para residuos
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

Salida:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

Aquí está el resumen de la tabla anterior:

Resumen del Modelo

El modelo es un modelo de regresión de Mínimos Cuadrados Ordinarios, que es un tipo de modelo de regresión lineal. La variable dependiente es MedHouseValue, y el modelo tiene un valor de R-cuadrado de 0.485, lo que indica que aproximadamente el 48.5% de la variación en MedHouseValue puede ser explicada por las variables independientes. El valor ajustado de R-cuadrado es 0.484, que es una versión modificada de R-cuadrado que penaliza al modelo por incluir variables independientes adicionales.

Ajuste del Modelo

El modelo fue ajustado utilizando el método de Mínimos Cuadrados, y la estadística F es 5173, lo que indica que el modelo es un buen ajuste. La probabilidad de observar una estadística F al menos tan extrema como la observada, asumiendo que la hipótesis nula es verdadera, es aproximadamente 0. Esto sugiere que el modelo es estadísticamente significativo.

Coeficientes del Modelo

Los coeficientes del modelo son los siguientes:

• El término constante es 2.0679, lo que indica que cuando todas las variables independientes son 0, el valor predicho de MedHouseValue es aproximadamente 2.0679.
• El coeficiente para x1 (En este caso MedInc) es 0.8300, lo que indica que por cada aumento de una unidad en MedInc, el valor predicho de MedHouseValue aumenta aproximadamente en 0.83 unidades, asumiendo que todas las demás variables independientes se mantienen constantes.
• El coeficiente para x2 (En este caso AveRooms) es -0.1000, lo que indica que por cada aumento de una unidad en x2, el valor predicho de MedHouseValue disminuye aproximadamente en 0.10 unidades, asumiendo que todas las demás variables independientes se mantienen constantes.
• El coeficiente para x3 (En este caso AveOccup) es -0.0397, lo que indica que por cada aumento de una unidad en x3, el valor predicho de MedHouseValue disminuye aproximadamente en 0.04 unidades, asumiendo que todas las demás variables independientes se mantienen constantes.

Diagnóstico del Modelo

Los diagnósticos del modelo son los siguientes:

• La estadística de prueba Omnibus es 3981.290, lo que indica que los residuos no se distribuyen normalmente.
• La estadística de Durbin-Watson es 1.983, lo que indica que no hay autocorrelación significativa en los residuos.
• La estadística de prueba Jarque-Bera es 11583.284, lo que indica que los residuos no se distribuyen normalmente.
• La asimetría de los residuos es 1.260, lo que indica que los residuos están sesgados hacia la derecha.
• La curtosis de los residuos es 6.239, lo que indica que los residuos son leptocúrticos (es decir, tienen un pico más alto y colas más pesadas que una distribución normal).
• El número de condición es 1.42, lo que indica que el modelo no es sensible a pequeños cambios en los datos.

Manejo de la Multicolinealidad

La multicolinealidad es un problema común en la regresión lineal múltiple, donde dos o más variables independientes están altamente correlacionadas entre sí. Esto puede llevar a estimaciones inestables e poco confiables de los coeficientes.

Para detectar y manejar la multicolinealidad, puedes utilizar el Factor de Inflación de la Varianza. El VIF mide cuánto aumenta la varianza de un coeficiente de regresión estimado si tus predictores están correlacionados. Un VIF de 1 significa que no hay correlación entre un predictor dado y los otros predictores. Los valores de VIF que exceden 5 o 10 indican una cantidad problemática de colinealidad.

En el bloque de código a continuación, vamos a calcular el VIF para cada variable independiente en nuestro modelo. Si algún valor de VIF está por encima de 5, deberías considerar eliminar la variable del modelo.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# Gráfico de Barras para los Valores de VIF
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

Resultado:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

Los valores de VIF para cada característica son los siguientes:

• MedInc: El valor de VIF es 1.120166, lo que indica una correlación muy baja con otras variables independientes. Esto sugiere que MedInc no está altamente correlacionado con otras variables independientes en el modelo.
• AveRooms: El valor de VIF es 1.119797, lo que indica una correlación muy baja con otras variables independientes. Esto sugiere que AveRooms no está altamente correlacionado con otras variables independientes en el modelo.
• AveOccup: El valor de VIF es 1.000488, lo que indica que no hay correlación con otras variables independientes. Esto sugiere que AveOccup no está correlacionado con otras variables independientes en el modelo.

En general, estos valores de VIF están por debajo de 5, lo que indica que no hay multicolinealidad significativa entre las variables independientes en el modelo. Esto sugiere que el modelo es estable y confiable, y que los coeficientes de las variables independientes no se ven significativamente afectados por la multicolinealidad.

Técnicas de Validación Cruzada

La validación cruzada es una técnica utilizada para evaluar el rendimiento de un modelo de aprendizaje automático. Es un procedimiento de remuestreo utilizado para evaluar un modelo si tenemos una muestra de datos limitada. El procedimiento tiene un único parámetro llamado k que se refiere al número de grupos en los que se dividirá una muestra de datos dada. Por lo tanto, el procedimiento se llama a menudo validación cruzada k-fold.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# Gráfico de Línea para Puntuaciones de Validación Cruzada
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

Salida:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

Las puntuaciones de validación cruzada indican qué tan bien se desempeña el modelo en datos no vistos. Las puntuaciones van desde 0.31191043 hasta 0.51269138, lo que indica que el rendimiento del modelo varía en diferentes pliegues. Una puntuación más alta indica un mejor rendimiento.

La puntuación media del R^2 CV es 0.41864482644003276, lo que sugiere que, en promedio, el modelo explica alrededor del 41.86% de la varianza en la variable objetivo. Esto es un nivel moderado de explicación, lo que indica que el modelo es algo efectivo para predecir la variable objetivo pero podría beneficiarse de una mejora o refinamiento adicional.

Estas puntuaciones se pueden utilizar para evaluar la generalización del modelo e identificar áreas potenciales de mejora.

Métodos de selección de características

El método de Eliminación Recursiva de Características es una técnica de selección de características que elimina recursivamente las características menos importantes hasta alcanzar un número especificado de características. Este método es particularmente útil cuando se trata de un gran número de características y el objetivo es seleccionar un subconjunto de las características más informativas.

En el código proporcionado, primero se importa la clase RFE de sklearn.feature_selection. Luego se crea una instancia de RFE con un estimador especificado (en este caso, LinearRegression) y se establece n_features_to_select en 2, lo que indica que queremos seleccionar las 2 mejores características.

A continuación, ajustamos el objeto RFE a nuestras características escaladas X_scaled y a la variable objetivo y. El atributo support_ del objeto RFE devuelve una máscara booleana que indica qué características fueron seleccionadas.

Para visualizar la clasificación de características, creamos un DataFrame con los nombres de las características y sus clasificaciones correspondientes. El atributo ranking_ del objeto RFE devuelve la clasificación de cada característica, con valores más bajos indicando características más importantes. Luego, trazamos un gráfico de barras de las clasificaciones de las características, ordenadas por sus valores de clasificación. Este gráfico nos ayuda a entender la importancia relativa de cada característica en el modelo.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# Gráfico de barras de las clasificaciones de características
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

Salida:

Selected Features: [ True  True False]

Según el gráfico anterior, las 2 características más adecuadas son MedInc y AveRooms. Esto también se puede verificar por la salida del modelo anterior, ya que la variable dependiente MedHouseValue depende principalmente de MedInc y AveRooms.

Preguntas frecuentes

¿Cómo se implementa la regresión lineal múltiple en Python?

Para implementar la regresión lineal múltiple en Python, puedes usar bibliotecas como statsmodels o scikit-learn. Aquí tienes una visión general rápida utilizando scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# Datos de ejemplo
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # Variables predictoras
y = np.array([5, 7, 9, 11])  # Variable objetivo

# Crear y ajustar el modelo
model = LinearRegression()
model.fit(X, y)

# Obtener coeficientes e intercepción
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# Realizar predicciones
predictions = model.predict(X)
print("Predictions:", predictions)

Esto demuestra cómo ajustar el modelo, obtener los coeficientes y realizar predicciones.

¿Cuáles son los supuestos de la regresión lineal múltiple en Python?

La regresión lineal múltiple se basa en varios supuestos para garantizar resultados válidos:

1. Linealidad: La relación entre las variables predictoras y la variable objetivo es lineal.
2. Independencia: Las observaciones son independientes entre sí.
3. Homocedasticidad: La varianza de los residuos es constante en todos los niveles de las variables independientes.
4. Normalidad de los Residuos: Los residuos siguen una distribución normal.
5. Sin multicolinealidad: Las variables independientes no están altamente correlacionadas entre sí.

Puedes probar estas suposiciones utilizando herramientas como gráficos residuales, Factor de Inflación de la Varianza (VIF) o pruebas estadísticas.

¿Cómo se interpretan los resultados de regresión múltiple en Python?

Las métricas clave de los resultados de regresión incluyen:

1. Coeficientes (coef_): Indican el cambio en la variable objetivo por un cambio de unidad en el predictor correspondiente, manteniendo constantes las demás variables.

Ejemplo: Un coeficiente de 2 para X1 significa que la variable objetivo aumenta en 2 por cada aumento de 1 unidad en X1, manteniendo constantes las demás variables.

2.Intercepción (intercept_): Representa el valor predicho de la variable objetivo cuando todos los predictores son cero.

3.R-cuadrado: Explica la proporción de la varianza en la variable objetivo explicada por los predictores.

Ejemplo: Un R^2 de 0.85 significa que el 85% de la variabilidad en la variable objetivo es explicada por el modelo.

4.Valores p (en statsmodels): Evalúan la significancia estadística de los predictores. Un valor p < 0.05 indica típicamente que un predictor es significativo.

¿Cuál es la diferencia entre la regresión lineal simple y múltiple en Python?

Conclusión

En este tutorial completo, aprendiste a implementar Regresión Lineal Múltiple utilizando el Conjunto de Datos de Viviendas de California. Abordaste aspectos cruciales como la multicolinealidad, la validación cruzada, la selección de características y la regularización, lo que proporciona una comprensión profunda de cada concepto. También aprendiste a incorporar visualizaciones para ilustrar residuos, importancia de características y rendimiento general del modelo. Ahora puedes construir fácilmente modelos de regresión robustos en Python y aplicar estas habilidades a problemas del mundo real.