Régression Linéaire Multiple en Python : Un Guide Complet

Introduction

La régression linéaire multiple est une technique statistique fondamentale utilisée pour modéliser la relation entre une variable dépendante et plusieurs variables indépendantes. En Python, des outils comme scikit-learn et statsmodels offrent des implémentations robustes pour l’analyse de régression. Ce tutoriel vous guidera à travers l’implémentation, l’interprétation et l’évaluation des modèles de régression linéaire multiple en utilisant Python.

Prérequis

Avant de plonger dans l’implémentation, assurez-vous de disposer des éléments suivants :

• Une compréhension de base de Python. Vous pouvez vous référer au Tutoriel Python pour débutants.
• Familiarité avec scikit-learn pour les tâches d’apprentissage automatique. Vous pouvez vous référer au Tutoriel Python scikit-learn.
• Compréhension des concepts de visualisation des données en Python. Vous pouvez consulter Comment tracer des données en Python 3 en utilisant matplotlib et Analyses et visualisations de données avec pandas et Jupyter Notebook en Python 3.
• Python 3.x est installé avec les bibliothèques suivantes numpy, pandas, matplotlib, seaborn, scikit-learn, et statsmodels installées.

Qu’est-ce que la régression linéaire multiple?

La régression linéaire multiple (MLR) est une méthode statistique qui modélise la relation entre une variable dépendante et deux ou plusieurs variables indépendantes. C’est une extension de la régression linéaire simple, qui modélise la relation entre une variable dépendante et une seule variable indépendante. En MLR, la relation est modélisée à l’aide de la formule:

Où:

Exemple : Prédire le prix d’une maison en fonction de sa taille, du nombre de chambres et de l’emplacement. Dans ce cas, il y a trois variables indépendantes, c’est-à-dire la taille, le nombre de chambres et l’emplacement, et une variable dépendante, c’est-à-dire le prix, qui est la valeur à prédire.

Hypothèses de la régression linéaire multiple

Avant de mettre en œuvre la régression linéaire multiple, il est essentiel de s’assurer que les hypothèses suivantes sont respectées :

1. Linéarité: La relation entre la variable dépendante et les variables indépendantes est linéaire.

2. Indépendance des erreurs: Les résidus (erreurs) sont indépendants les uns des autres. Cela est souvent vérifié à l’aide du test de Durbin-Watson.

3. Homoscédasticité: La variance des résidus est constante à tous les niveaux des variables indépendantes. Un graphique des résidus peut aider à vérifier cela.

4. Aucune Multicolinéarité: Les variables indépendantes ne sont pas fortement corrélées. Facteur d’Inflation de Variance (VIF) est couramment utilisé pour détecter la multicolinéarité.

5. Normalité des Résidus: Les résidus doivent suivre une distribution normale. Cela peut être vérifié à l’aide d’un diagramme Q-Q.

6. Influence des Valeurs Abérantes: Les valeurs aberrantes ou les points à forte influence ne doivent pas influencer de manière disproportionnée le modèle.

Ces hypothèses garantissent que le modèle de régression est valide et que les résultats sont fiables. Le non-respect de ces hypothèses peut conduire à des résultats biaisés ou trompeurs.

Prétraiter les données

Dans cette section, vous apprendrez à utiliser le modèle de régression linéaire multiple en Python pour prédire les prix des maisons en fonction des caractéristiques du Jeu de données sur le logement en Californie. Vous apprendrez comment prétraiter les données, ajuster un modèle de régression et évaluer sa performance en traitant des défis courants tels que la multicolinéarité, les valeurs aberrantes et la sélection des caractéristiques.

Étape 1 – Charger le jeu de données

Vous utiliserez le Jeu de données sur le logement en Californie, un ensemble de données populaire pour les tâches de régression. Cet ensemble de données contient 13 caractéristiques sur des maisons dans les banlieues de Boston et leur prix médian correspondant.

Tout d’abord, installons les packages nécessaires :

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # Importez la fonction fetch_california_housing de sklearn.datasets pour charger le jeu de données sur le logement en Californie.
import pandas as pd  # Importez pandas pour la manipulation et l'analyse des données.
import numpy as np  # Importez numpy pour le calcul numérique.

# Chargez le jeu de données sur le logement en Californie en utilisant la fonction fetch_california_housing.
housing = fetch_california_housing()

# Convertissez les données du jeu de données en un DataFrame pandas, en utilisant les noms des caractéristiques comme en-têtes de colonnes.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# Ajoutez la variable cible 'MedHouseValue' au DataFrame, en utilisant les valeurs cibles du jeu de données.
housing_df['MedHouseValue'] = housing.target

# Affichez les premières lignes du DataFrame pour avoir un aperçu du jeu de données.
print(housing_df.head())

Vous devriez observer la sortie suivante du jeu de données :

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

Voici la signification de chacun des attributs :

Étape 2 – Prétraiter les Données

Vérifiez les Valeurs Manquantes

Assurez-vous qu’il n’y a pas de valeurs manquantes dans le jeu de données qui pourraient affecter l’analyse.

print(housing_df.isnull().sum())

Sortie :

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

Sélection des Caractéristiques

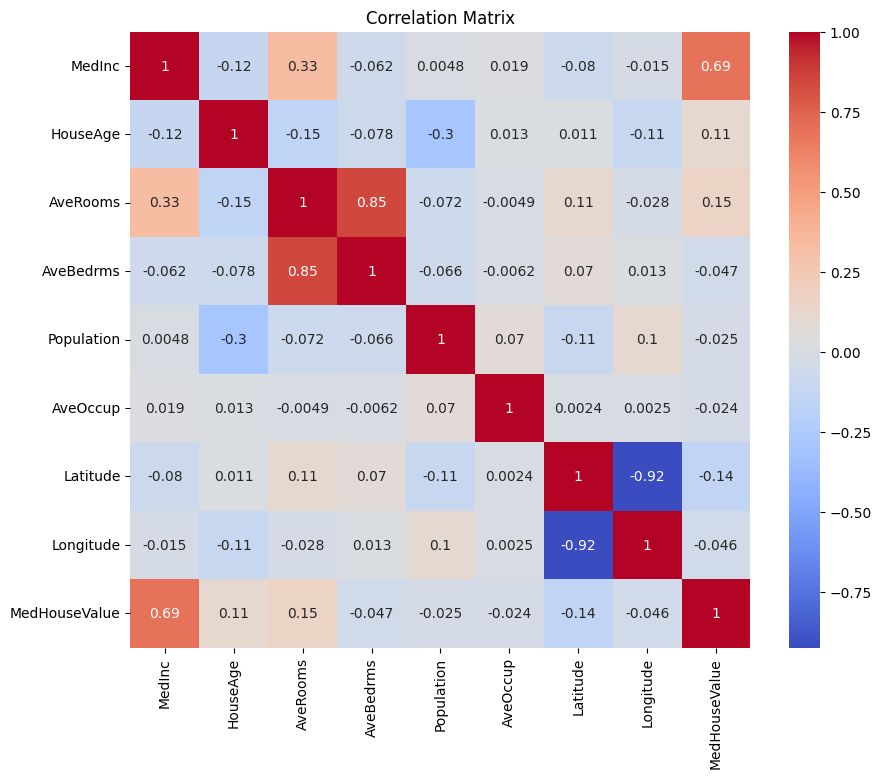
Commençons par créer une matrice de corrélation pour comprendre les dépendances entre les variables.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

Sortie :

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

Vous pouvez analyser la matrice de corrélation ci-dessus pour sélectionner les variables dépendantes et indépendantes pour notre modèle de régression. La matrice de corrélation fournit des informations sur les relations entre chaque paire de variables dans le jeu de données.

Dans la matrice de corrélation donnée, MedHouseValue est la variable dépendante, car c’est la variable que nous essayons de prédire. Les variables indépendantes ont une corrélation significative avec MedHouseValue.

Sur la base de la matrice de corrélation, vous pouvez identifier les variables indépendantes suivantes qui ont une corrélation significative avec MedHouseValue :

• MedInc : Cette variable a une forte corrélation positive (0.688075) avec MedHouseValue, indiquant qu’à mesure que le revenu médian augmente, la valeur médiane des maisons a également tendance à augmenter.
• AveRooms : Cette variable a une corrélation positive modérée (0.151948) avec MedHouseValue, suggérant qu’à mesure que le nombre moyen de chambres par ménage augmente, la valeur médiane des maisons a également tendance à augmenter.
• AveOccup : Cette variable a une faible corrélation négative (-0,023737) avec MedHouseValue, ce qui indique qu’à mesure que l’occupation moyenne par ménage augmente, la valeur médiane des maisons tend à diminuer, mais l’effet est relativement faible.

En sélectionnant ces variables indépendantes, vous pouvez construire un modèle de régression qui capture les relations entre ces variables et MedHouseValue, nous permettant de faire des prédictions sur la valeur médiane des maisons en fonction du revenu médian, du nombre moyen de pièces et de l’occupation moyenne.

Vous pouvez également tracer la matrice de corrélation en Python en utilisant le code ci-dessous :

import seaborn as sns
import matplotlib.pyplot as plt

# En supposant que 'housing_df' est le DataFrame contenant les données
# Traçant la matrice de corrélation
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

Vous vous concentrerez sur quelques caractéristiques clés pour la simplicité, basées sur ce qui précède, telles que MedInc (revenu médian), AveRooms (nombre moyen de pièces par ménage) et AveOccup (occupation moyenne par ménage).

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

Le bloc de code ci-dessus sélectionne des caractéristiques spécifiques du DataFrame housing_df pour analyse. Les caractéristiques sélectionnées sont MedInc, AveRooms et AveOccup, qui sont stockées dans la liste selected_features.

Le DataFrame housing_df est ensuite sous-ensemble pour inclure uniquement ces caractéristiques sélectionnées et le résultat est stocké dans la liste X.

La variable cible MedHouseValue est extraite de housing_df et stockée dans la liste y.

Normalisation des caractéristiques

Vous utiliserez la standardisation pour garantir que toutes les caractéristiques sont sur la même échelle, améliorant ainsi la performance et la comparabilité du modèle.

La standardisation est une technique de prétraitement qui met à l’échelle les caractéristiques numériques pour avoir une moyenne de 0 et un écart type de 1. Ce processus garantit que toutes les caractéristiques sont sur la même échelle, ce qui est essentiel pour les modèles d’apprentissage automatique sensibles à l’échelle des caractéristiques d’entrée. En standardisant les caractéristiques, vous pouvez améliorer la performance et la comparabilité du modèle en réduisant l’effet des caractéristiques ayant de grandes plages qui dominent le modèle.

from sklearn.preprocessing import StandardScaler

# Initialiser l'objet StandardScaler
scaler = StandardScaler()

# Ajuster le scaler aux données et les transformer
X_scaled = scaler.fit_transform(X)

# Imprimer les données mises à l'échelle
print(X_scaled)

Sortie:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

La sortie représente les valeurs mises à l’échelle des caractéristiques MedInc, AveRooms et AveOccup après l’application du StandardScaler. Les valeurs sont désormais centrées autour de 0 avec un écart type de 1, garantissant que toutes les caractéristiques sont sur la même échelle.

La première ligne [ 2.34476576 0.62855945 -0.04959654] indique que pour le premier point de données, la valeur mise à l’échelle de MedInc est 2.34476576, AveRooms est 0.62855945, et AveOccup est -0.04959654. De même, la deuxième ligne [ 2.33223796 0.32704136 -0.09251223] représente les valeurs mises à l’échelle pour le deuxième point de données, et ainsi de suite.

Les valeurs mises à l’échelle varient d’environ -1,14259331 à 2,34476576, ce qui indique que les caractéristiques sont désormais normalisées et comparables. Cela est essentiel pour les modèles d’apprentissage automatique qui sont sensibles à l’échelle des caractéristiques d’entrée, car cela empêche les caractéristiques avec de grandes plages de dominer le modèle.

Implémenter la régression linéaire multiple

Maintenant que vous avez terminé le prétraitement des données, implémentons la régression linéaire multiple en Python.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# Le modèle 'LinearRegression' est initialisé et ajusté aux données d'entraînement.
model = LinearRegression()
model.fit(X_train, y_train)

# Le modèle est utilisé pour prédire la variable cible pour l'ensemble de test.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

La fonction train_test_split est utilisée pour diviser les données en ensembles d’entraînement et de test. Ici, 80 % des données sont utilisées pour l’entraînement et 20 % pour le test.

Le modèle est évalué à l’aide de l’erreur quadratique moyenne et du R-carré. L’erreur quadratique moyenne (MSE) mesure la moyenne des carrés des erreurs ou des écarts.

Le R-carré (R2) est une mesure statistique qui représente la proportion de la variance d’une variable dépendante qui est expliquée par une variable indépendante ou des variables dans un modèle de régression.

Sortie :

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

La sortie ci-dessus fournit deux indicateurs clés pour évaluer la performance du modèle de régression linéaire multiple :

Erreur quadratique moyenne (EQM) : 0.7006855912225249
L’EQM mesure la différence moyenne au carré entre les valeurs prédites et les valeurs réelles de la variable cible. Un EQM plus bas indique de meilleures performances du modèle, car cela signifie que le modèle fait des prédictions plus précises. Dans ce cas, l’EQM est 0.7006855912225249, ce qui indique que le modèle n’est pas parfait mais possède un niveau de précision raisonnable. Les valeurs de l’EQM devraient généralement se rapprocher de 0, des valeurs plus basses indiquant de meilleures performances.

R-carré (R2) : 0.4652924370503557
R-carré mesure la proportion de la variance dans la variable dépendante qui peut être prédite à partir des variables indépendantes. Il varie de 0 à 1, où 1 représente une prédiction parfaite et 0 indique qu’il n’y a aucune relation linéaire. Dans ce cas, la valeur de R-carré est 0.4652924370503557, ce qui indique qu’environ 46,53 % de la variance de la variable cible peut être expliquée par les variables indépendantes utilisées dans le modèle. Cela suggère que le modèle est capable de capturer une partie significative des relations entre les variables mais pas toutes.

Examinons quelques graphiques importants :

# Graphique des résidus
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# Graphique Prédit vs Réel
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

Utilisation de statsmodels

La bibliothèque Statsmodels en Python est un outil puissant pour l’analyse statistique. Elle offre un large éventail de modèles et de tests statistiques, y compris la régression linéaire, l’analyse des séries chronologiques et des méthodes non paramétriques.

Dans le cadre de la régression linéaire multiple, statsmodels peut être utilisé pour ajuster un modèle linéaire aux données, puis pour effectuer divers tests et analyses statistiques sur le modèle. Cela peut être particulièrement utile pour comprendre les relations entre les variables indépendantes et dépendantes, et pour faire des prédictions basées sur le modèle.

import statsmodels.api as sm

# Ajouter une constante au modèle
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# Diagramme Q-Q pour les résidus
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

Sortie:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

Voici le résumé du tableau ci-dessus :

Résumé du modèle

Le modèle est un modèle de régression des moindres carrés ordinaires, qui est un type de modèle de régression linéaire. La variable dépendante est MedHouseValue, et le modèle a une valeur de R² de 0,485, ce qui indique qu’environ 48,5 % de la variation de MedHouseValue peut être expliquée par les variables indépendantes. La valeur ajustée de R² est de 0,484, qui est une version modifiée de R² qui pénalise le modèle pour l’inclusion de variables indépendantes supplémentaires.

Ajustement du modèle

Le modèle a été ajusté en utilisant la méthode des moindres carrés, et la statistique F est de 5173, ce qui indique que le modèle est bien ajusté. La probabilité d’observer une statistique F au moins aussi extrême que celle observée, en supposant que l’hypothèse nulle est vraie, est d’environ 0. Cela suggère que le modèle est statistiquement significatif.

Coefficients du modèle

Les coefficients du modèle sont les suivants :

• Le terme constant est de 2,0679, ce qui indique que lorsque toutes les variables indépendantes sont à 0, la MedHouseValue prédite est d’environ 2,0679.
• Le coefficient pour x1 (dans ce cas, MedInc) est de 0,8300, ce qui indique que pour chaque augmentation d’une unité de MedInc, la MedHouseValue prédite augmente d’environ 0,83 unités, en supposant que toutes les autres variables indépendantes sont maintenues constantes.
• Le coefficient pour x2 (dans ce cas AveRooms) est de -0,1000, ce qui indique que pour chaque augmentation d’une unité de x2, la valeur prédite de MedHouseValue diminue d’environ 0,10 unité, en supposant que toutes les autres variables indépendantes sont maintenues constantes.
• Le coefficient pour x3 (dans ce cas AveOccup) est de -0,0397, ce qui indique que pour chaque augmentation d’une unité de x3, la valeur prédite de MedHouseValue diminue d’environ 0,04 unité, en supposant que toutes les autres variables indépendantes sont maintenues constantes.

Diagnostic du modèle

Les diagnostics du modèle sont les suivants :

• La statistique du test Omnibus est de 3981,290, ce qui indique que les résidus ne suivent pas une distribution normale.
• La statistique de Durbin-Watson est de 1,983, ce qui indique qu’il n’y a pas d’autocorrélation significative dans les résidus.
• La statistique du test de Jarque-Bera est de 11583,284, ce qui indique que les résidus ne suivent pas une distribution normale.
• La skewness des résidus est de 1,260, ce qui indique qu’ils sont asymétriques vers la droite.
• La kurtosis des résidus est de 6,239, ce qui indique qu’ils sont leptokurtiques (c’est-à-dire qu’ils ont un pic plus élevé et des queues plus lourdes qu’une distribution normale).
• Le nombre de condition est de 1,42, ce qui indique que le modèle n’est pas sensible aux petites variations des données.

Gestion de la multicolinéarité

La multicolinéarité est un problème courant dans la régression linéaire multiple, où deux ou plusieurs variables indépendantes sont fortement corrélées entre elles. Cela peut conduire à des estimations instables et peu fiables des coefficients.

Pour détecter et gérer la multicolinéarité, vous pouvez utiliser le Facteur d’Inflation de Variance. Le VIF mesure combien la variance d’un coefficient de régression estimé augmente si vos prédicteurs sont corrélés. Un VIF de 1 signifie qu’il n’y a pas de corrélation entre un prédicteur donné et les autres prédicteurs. Des valeurs VIF dépassant 5 ou 10 indiquent une quantité problématique de collinéarité.

Dans le bloc de code ci-dessous, calculons le VIF pour chaque variable indépendante de notre modèle. Si une valeur VIF est supérieure à 5, vous devriez envisager de supprimer la variable du modèle.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# Graphique à barres pour les valeurs VIF
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

Sortie:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

Les valeurs VIF pour chaque caractéristique sont les suivantes :

• MedInc : La valeur VIF est 1.120166, indiquant une très faible corrélation avec les autres variables indépendantes. Cela suggère que MedInc n’est pas fortement corrélé avec les autres variables indépendantes dans le modèle.
• AveRooms : La valeur VIF est 1.119797, indiquant une très faible corrélation avec les autres variables indépendantes. Cela suggère que AveRooms n’est pas fortement corrélé avec les autres variables indépendantes dans le modèle.
• AveOccup: La valeur VIF est de 1,000488, ce qui indique qu’il n’y a pas de corrélation avec les autres variables indépendantes. Cela suggère que AveOccup n’est pas corrélé avec les autres variables indépendantes du modèle.

En général, ces valeurs VIF sont toutes inférieures à 5, ce qui indique qu’il n’y a pas de multicollinéarité significative entre les variables indépendantes du modèle. Cela suggère que le modèle est stable et fiable, et que les coefficients des variables indépendantes ne sont pas significativement affectés par la multicollinéarité.

Techniques de validation croisée

La validation croisée est une technique utilisée pour évaluer les performances d’un modèle d’apprentissage automatique. Il s’agit d’une procédure de rééchantillonnage utilisée pour évaluer un modèle lorsque nous disposons d’un échantillon de données limité. La procédure a un seul paramètre appelé k qui fait référence au nombre de groupes dans lesquels un échantillon de données donné doit être divisé. En tant que telle, la procédure est souvent appelée validation croisée k-fold.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# Graphique en ligne pour les scores de validation croisée
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

Sortie :

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

Les scores de validation croisée indiquent la performance du modèle sur des données invisibles. Les scores varient de 0,31191043 à 0,51269138, ce qui indique que les performances du modèle varient d’un pli à l’autre. Un score plus élevé indique de meilleures performances.

Le score moyen CV R^2 est de 0.41864482644003276, ce qui suggère qu’en moyenne, le modèle explique environ 41,86 % de la variance de la variable cible. C’est un niveau d’explication modéré, indiquant que le modèle est quelque peu efficace pour prédire la variable cible mais pourrait bénéficier d’une amélioration ou d’un perfectionnement supplémentaire.

Ces scores peuvent être utilisés pour évaluer la généralisabilité du modèle et identifier les domaines potentiels d’amélioration.

Méthodes de sélection de caractéristiques

La méthode Élimination Récursive de Caractéristiques est une technique de sélection de caractéristiques qui élimine de manière récursive les caractéristiques les moins importantes jusqu’à ce qu’un nombre spécifié de caractéristiques soit atteint. Cette méthode est particulièrement utile lorsqu’il s’agit d’un grand nombre de caractéristiques et que l’objectif est de sélectionner un sous-ensemble des caractéristiques les plus informatives.

Dans le code fourni, vous importez d’abord la classe RFE de sklearn.feature_selection. Ensuite, créez une instance de RFE avec un estimateur spécifié (dans ce cas, LinearRegression) et définissez n_features_to_select à 2, indiquant que nous voulons sélectionner les 2 meilleures caractéristiques.

Ensuite, nous adaptons l’objet RFE à nos fonctionnalités mises à l’échelle X_scaled et à la variable cible y. L’attribut support_ de l’objet RFE renvoie un masque booléen indiquant quelles fonctionnalités ont été sélectionnées.

Pour visualiser le classement des fonctionnalités, vous créez un DataFrame avec les noms des fonctionnalités et leurs classements correspondants. L’attribut ranking_ de l’objet RFE renvoie le classement de chaque fonctionnalité, les valeurs plus basses indiquant des fonctionnalités plus importantes. Vous tracez ensuite un graphique à barres des classements des fonctionnalités, triées par leurs valeurs de classement. Ce graphique nous aide à comprendre l’importance relative de chaque fonctionnalité dans le modèle.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# Graphique à barres des classements des fonctionnalités
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

Sortie:

Selected Features: [ True  True False]

Basé sur le graphique ci-dessus, les 2 fonctionnalités les plus adaptées sont MedInc et AveRooms. Cela peut également être vérifié par la sortie du modèle ci-dessus car la variable dépendante MedHouseValue dépend principalement de MedInc et AveRooms.

FAQs

Comment implémenter une régression linéaire multiple en Python?

Pour implémenter une régression linéaire multiple en Python, vous pouvez utiliser des bibliothèques telles que statsmodels ou scikit-learn. Voici un aperçu rapide en utilisant scikit-learn:

from sklearn.linear_model import LinearRegression
import numpy as np

# Données d'exemple
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # Variables prédictives
y = np.array([5, 7, 9, 11])  # Variable cible

# Créer et ajuster le modèle
model = LinearRegression()
model.fit(X, y)

# Obtenir les coefficients et l'intercept
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# Faire des prédictions
predictions = model.predict(X)
print("Predictions:", predictions)

Ceci démontre comment ajuster le modèle, obtenir les coefficients et faire des prédictions.

Quelles sont les hypothèses de la régression linéaire multiple en Python ?

La régression linéaire multiple repose sur plusieurs hypothèses pour garantir des résultats valides :

1. Linéarité : La relation entre les variables prédictives et la variable cible est linéaire.
2. Indépendance : Les observations sont indépendantes les unes des autres.
3. Homoscédasticité : La variance des résidus (erreurs) est constante à tous les niveaux des variables indépendantes.
4. Normalité des résidus : Les résidus suivent une distribution normale.
5. Pas de Multicolinéarité: Les variables indépendantes ne sont pas fortement corrélées entre elles.

Vous pouvez tester ces hypothèses en utilisant des outils tels que des graphiques résiduels, le Facteur d’Inflation de la Variance (VIF), ou des tests statistiques.

Comment interpréter les résultats de la régression multiple en Python?

Les principales métriques des résultats de la régression comprennent:

1. Coefficients (coef_): Indiquent le changement de la variable cible pour un changement unitaire du prédicteur correspondant, en maintenant les autres variables constantes.

Exemple: Un coefficient de 2 pour X1 signifie que la variable cible augmente de 2 pour chaque augmentation de 1 unité de X1, en maintenant les autres variables constantes.

2.Intercept (intercept_): Représente la valeur prédite de la variable cible lorsque tous les prédicteurs sont nuls.

3.R-carré: Explique la proportion de la variance de la variable cible expliquée par les prédicteurs.

Exemple: Un R^2 de 0,85 signifie que 85% de la variabilité de la variable cible est expliquée par le modèle.

4.Valeurs P (dans statsmodels): Évaluent la signification statistique des prédicteurs. Une valeur p< 0,05 indique généralement qu’un prédicteur est significatif.

Quelle est la différence entre la régression linéaire simple et multiple en Python?

Conclusion

Dans ce tutoriel complet, vous avez appris à mettre en œuvre la régression linéaire multiple en utilisant le jeu de données sur le logement en Californie. Vous avez abordé des aspects cruciaux tels que la multicolinéarité, la validation croisée, la sélection des caractéristiques et la régularisation, offrant une compréhension approfondie de chaque concept. Vous avez également appris à incorporer des visualisations pour illustrer les résidus, l’importance des caractéristiques et les performances globales du modèle. Vous pouvez désormais facilement construire des modèles de régression robustes en Python et appliquer ces compétences à des problèmes concrets.