파이썬에서 다중 선형 회귀: 포괄적 가이드

소개

다중 선형 회귀는 종속 변수와 여러 독립 변수 간의 관계를 모델링하는 데 사용되는 기본적인 통계 기법입니다. Python에서는 scikit-learn 및 statsmodels와 같은 도구들이 회귀 분석을 위한 견고한 구현을 제공합니다. 본 자습서에서는 Python을 사용하여 다중 선형 회귀 모델을 구현, 해석 및 평가하는 방법을 안내하겠습니다.

필수 요구 사항

구현에 들어가기 전에 다음 사항을 준비해야 합니다:

• Python의 기본적인 이해. 초보자를 위한 Python 자습서를 참조할 수 있습니다.
• 기계 학습 작업을 위한 scikit-learn에 대한 이해. Python scikit-learn 자습서를 참조할 수 있습니다.
• 파이썬에서 데이터 시각화 개념 이해하기. 파이썬 3에서 matplotlib을 사용하여 데이터 플롯하는 방법와 파이썬 3에서 pandas 및 Jupyter Notebook을 사용한 데이터 분석 및 시각화를 참조할 수 있습니다.
• 다음 라이브러리 numpy, pandas, matplotlib, seaborn, scikit-learn, statsmodels가 설치된 파이썬 3.x.

다중 선형 회귀란?

다중 선형 회귀(MLR)는 종속 변수와 두 개 이상의 독립 변수 간의 관계를 모델링하는 통계적 방법입니다. 이는 종속 변수와 단일 독립 변수 간의 관계를 모델링하는 단순 선형 회귀의 확장입니다. MLR에서는 다음 공식을 사용하여 관계를 모델링합니다:

여기서:

예: 집의 크기, 침실 수 및 위치에 따라 집값 예측. 이 경우, 크기, 침실 수 및 위치라는 세 개의 독립 변수와 예측해야 할 값인 가격이라는 하나의 종속 변수가 있습니다.

다중 선형 회귀의 가정

다중 선형 회귀를 시행하기 전에는 다음 가정이 충족되었는지 확인하는 것이 중요합니다:

1. 선형성: 종속 변수와 독립 변수 간의 관계가 선형적이다.

2. 오차의 독립성: 잔차(오차)들은 서로 독립적이다. 이는 종종 Durbin-Watson 검정을 사용하여 확인된다.

3. 등분산성: 잔차의 분산이 독립 변수의 모든 수준에서 일정하다. 잔차 플롯을 통해 이를 확인할 수 있다.

4. 다중공선성이 없음: 독립 변수들 간에 높은 상관 관계가 없습니다. 분산 팽창 요인(VIF)은 다중공선성을 탐지하는 데 일반적으로 사용됩니다.

5. 잔차의 정규성: 잔차는 정규 분포를 따라야 합니다. 이는 Q-Q plot을 사용하여 확인할 수 있습니다.

6. 이상치 영향: 이상치나 높은 영향력을 가진 점은 모델에 지나치게 영향을 미치지 않아야 합니다.

이러한 가정들은 회귀 모델이 유효하며 결과가 신뢰할 수 있도록 합니다. 이러한 가정을 충족하지 못하면 편향된 또는 오도하는 결과로 이어질 수 있습니다.

데이터 전처리

이번 섹션에서는 캘리포니아 주택 데이터셋의 특징을 기반으로 주택 가격을 예측하기 위해 Python에서 다중 선형 회귀 모델을 사용하는 방법을 배웁니다. 데이터 전처리, 회귀 모델 적합, 성능 평가 방법을 배우고 다중 공선성, 이상치, 특징 선택과 같은 일반적인 문제를 다룹니다.

1단계 – 데이터셋 로드

회귀 작업에 널리 사용되는 캘리포니아 주택 데이터셋을 사용할 것입니다. 이 데이터셋은 보스턴 교외의 주택에 대한 13개의 특징과 해당 주택의 중간 가격 정보를 포함하고 있습니다.

먼저, 필요한 패키지를 설치해 보겠습니다:

pip install numpy pandas matplotlib seaborn scikit-learn statsmodels

from sklearn.datasets import fetch_california_housing  # sklearn.datasets에서 fetch_california_housing 함수를 임포트하여 캘리포니아 주택 데이터셋을 로드합니다.
import pandas as pd  # 데이터 조작 및 분석을 위해 pandas를 임포트합니다.
import numpy as np  # 수치 계산을 위해 numpy를 임포트합니다.

# fetch_california_housing 함수를 사용하여 캘리포니아 주택 데이터셋을 로드합니다.
housing = fetch_california_housing()

# 데이터셋의 데이터를 pandas DataFrame으로 변환하며, 특성 이름을 열 헤더로 사용합니다.
housing_df = pd.DataFrame(housing.data, columns=housing.feature_names)

# 데이터셋의 타겟 값을 사용하여 DataFrame에 타겟 변수 'MedHouseValue'를 추가합니다.
housing_df['MedHouseValue'] = housing.target

# 데이터셋의 개요를 파악하기 위해 DataFrame의 처음 몇 행을 표시합니다.
print(housing_df.head())

데이터셋의 다음 출력을 관찰해야 합니다:

 MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  Longitude  MedHouseValue
0  8.3252      41.0  6.984127   1.023810       322.0  2.555556     37.88    -122.23          4.526
1  8.3014      21.0  6.238137   0.971880      2401.0  2.109842     37.86    -122.22          3.585
2  7.2574      52.0  8.288136   1.073446       496.0  2.802260     37.85    -122.24          3.521
3  5.6431      52.0  5.817352   1.073059       558.0  2.547945     37.85    -122.25          3.413
4  3.8462      52.0  6.281853   1.081081       565.0  2.181467     37.85    -122.25          3.422

각 속성이 의미하는 바는 다음과 같습니다:

단계 2 – 데이터 전처리

결측값 확인

분석에 영향을 줄 수 있는 데이터셋 내 결측값이 있는지 확인합니다.

print(housing_df.isnull().sum())

결과:

MedInc           0
HouseAge         0
AveRooms         0
AveBedrms        0
Population       0
AveOccup         0
Latitude         0
Longitude        0
MedHouseValue    0
dtype: int64

특성 선택

먼저 상관 행렬을 작성하여 변수 간 종속성을 이해합니다.

correlation_matrix = housing_df.corr()
print(correlation_matrix['MedHouseValue'])

결과:

MedInc           0.688075
HouseAge         0.105623
AveRooms         0.151948
AveBedrms       -0.046701
Population      -0.024650
AveOccup        -0.023737
Latitude        -0.144160
Longitude       -0.045967
MedHouseValue    1.000000

상기 상관 행렬을 분석하여 회귀 모델의 종속 및 독립 변수를 선택할 수 있습니다. 상관 행렬은 데이터셋 내 각 변수 쌍 간의 관계에 대한 통찰을 제공합니다.

상기 상관 행렬에서 MedHouseValue는 예측하려는 변수이므로 종속 변수입니다. 독립 변수는 MedHouseValue와 유의한 상관 관계를 가지고 있습니다.

상관 행렬을 기반으로 MedHouseValue와 유의한 상관 관계를 가지는 다음 독립 변수를 식별할 수 있습니다:

• MedInc: 이 변수는 MedHouseValue와 강한 양의 상관 관계(0.688075)를 가지며, 중위 소득이 증가할수록 중위 주택 가치도 증가하는 경향을 나타냅니다.
• AveRooms: 이 변수는 MedHouseValue와 적당한 양의 상관 관계(0.151948)를 가지며, 가구 당 평균 방 수가 증가할수록 중위 주택 가치도 증가하는 경향을 나타냅니다.
• AveOccup: 이 변수는 MedHouseValue와 약한 음의 상관관계(-0.023737)를 가지고 있으며, 이는 가구당 평균 점유율이 증가함에 따라 중간 주택 가치가 감소하는 경향이 있음을 나타내지만, 그 영향은 상대적으로 작습니다.

이러한 독립 변수를 선택함으로써, 이 변수들과 MedHouseValue 간의 관계를 포착하는 회귀 모델을 구축할 수 있으며, 이를 통해 중간 소득, 평균 방 수 및 평균 점유율에 따라 중간 주택 가치를 예측할 수 있습니다.

아래의 코드를 사용하여 Python에서 상관 행렬을 플로팅할 수도 있습니다:

import seaborn as sns
import matplotlib.pyplot as plt

# 'housing_df'가 데이터를 포함하는 DataFrame이라고 가정합니다
# 상관 행렬 플로팅
plt.figure(figsize=(10, 8))
sns.heatmap(housing_df.corr(), annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

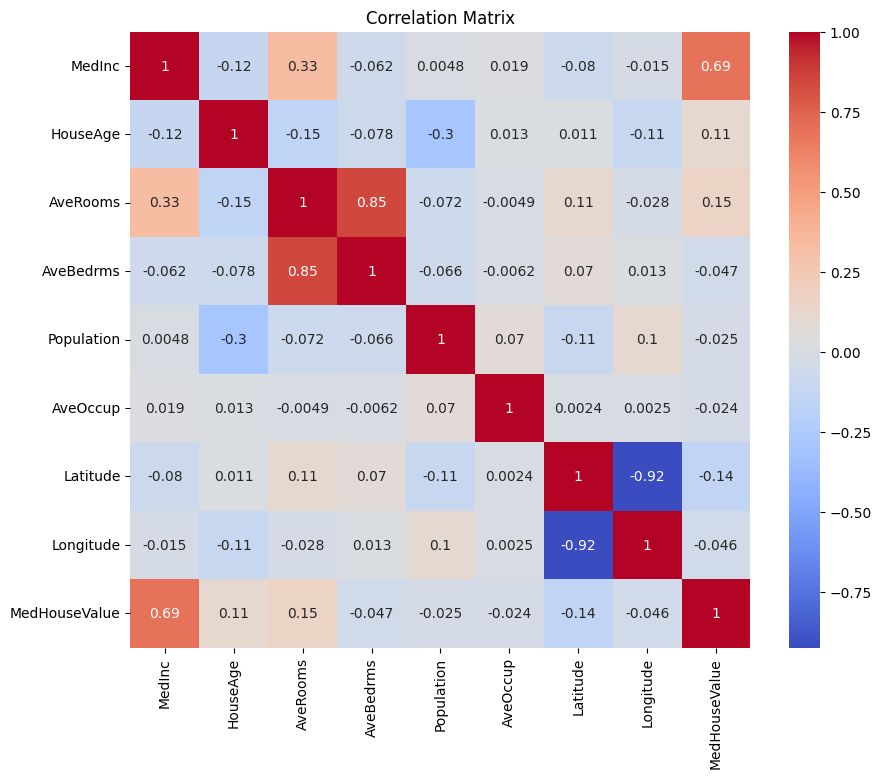
위의 내용을 바탕으로 MedInc (중간 소득), AveRooms (가구당 평균 방 수) 및 AveOccup (가구당 평균 점유율)과 같은 몇 가지 주요 특징에 집중할 것입니다.

selected_features = ['MedInc', 'AveRooms', 'AveOccup']
X = housing_df[selected_features]
y = housing_df['MedHouseValue']

위의 코드 블록은 분석을 위해 housing_df 데이터 프레임에서 특정 특징들을 선택합니다. 선택된 특징은 MedInc, AveRooms, AveOccup이며, 이들은 selected_features 리스트에 저장됩니다.

그런 다음 DataFrame housing_df는 이 선택된 특징만 포함하도록 서브셋되어 결과가 X 리스트에 저장됩니다.

타겟 변수 MedHouseValue는 housing_df에서 추출되어 y 리스트에 저장됩니다.

특징 스케일링

표준화를 사용하여 모든 특성이 동일한 범위에 있도록 하여 모델 성능과 비교 가능성을 향상시킵니다.

표준화는 숫자 특성을 평균 0, 표준 편차 1로 스케일링하는 전처리 기술입니다. 이 과정은 모든 특성이 동일한 범위에 있도록 보장하며, 이는 입력 특성의 범위에 민감한 머신러닝 모델에 필수적입니다. 특성을 표준화함으로써 범위가 큰 특성이 모델을 지배하는 영향을 줄여 모델 성능과 비교 가능성을 높일 수 있습니다.

from sklearn.preprocessing import StandardScaler

# StandardScaler 객체 초기화
scaler = StandardScaler()

# 데이터에 스케일러를 적합시키고 변환하기
X_scaled = scaler.fit_transform(X)

# 스케일된 데이터 출력하기
print(X_scaled)

출력:

[[ 2.34476576  0.62855945 -0.04959654]
[ 2.33223796  0.32704136 -0.09251223]
[ 1.7826994   1.15562047 -0.02584253]
...
[-1.14259331 -0.09031802 -0.0717345 ]
[-1.05458292 -0.04021111 -0.09122515]
[-0.78012947 -0.07044252 -0.04368215]]

출력은 StandardScaler를 적용한 후 특성 MedInc, AveRooms, AveOccup의 스케일된 값을 나타냅니다. 값들은 이제 0을 중심으로 표준 편차가 1이 되어 모든 특성이 동일한 범위에 있도록 보장합니다.

첫 번째 행 [ 2.34476576 0.62855945 -0.04959654]는 첫 번째 데이터 포인트에 대해 스케일된 MedInc 값이 2.34476576, AveRooms가 0.62855945, AveOccup가 -0.04959654임을 나타냅니다. 마찬가지로 두 번째 행 [ 2.33223796 0.32704136 -0.09251223]는 두 번째 데이터 포인트의 스케일된 값을 나타냅니다.

스케일 조정된 값은 대략 -1.14259331에서 2.34476576까지의 범위를 가지며, 특징들이 정규화되어 비교 가능해졌음을 나타냅니다. 이것은 입력 특징의 스케일에 민감한 기계 학습 모델에서 중요합니다. 이것은 큰 범위의 특징이 모델을 지배하는 것을 방지합니다.

다중 선형 회귀 구현

데이터 전처리를 완료했으므로 이제 파이썬에서 다중 선형 회귀를 구현해봅시다.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# 'LinearRegression' 모델이 초기화되고 훈련 데이터에 맞춰집니다.
model = LinearRegression()
model.fit(X_train, y_train)

# 모델은 테스트 세트에 대한 대상 변수를 예측하는 데 사용됩니다.
y_pred = model.predict(X_test)


print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("R-squared:", r2_score(y_test, y_pred))

train_test_split 함수를 사용하여 데이터를 훈련 및 테스트 세트로 분할합니다. 여기서 데이터의 80%는 훈련에 사용되고 20%는 테스트에 사용됩니다.

모델은 평균 제곱 오차(Mean Squared Error)와 R-제곱을 사용하여 평가됩니다. 평균 제곱 오차(MSE)는 오차 또는 편차의 제곱의 평균을 측정합니다.

R-제곱(R2)은 회귀 모델에서 종속 변수의 분산 중 독립 변수 또는 변수가 설명하는 비율을 나타내는 통계적 측정입니다.

출력:

Mean Squared Error: 0.7006855912225249
R-squared: 0.4652924370503557

위의 출력은 다중 선형 회귀 모델의 성능을 평가하는 데 사용되는 두 가지 주요 지표를 제공합니다:

평균 제곱 오차 (MSE): 0.7006855912225249
MSE는 타겟 변수의 예측값과 실제값 간의 평균 제곱 차이를 측정합니다. 낮은 MSE는 모델 성능이 더 좋다는 것을 나타내며, 이는 모델이 더 정확한 예측을 한다는 것을 의미합니다. 이 경우 MSE는 0.7006855912225249이며, 모델이 완벽하지는 않지만 합리적인 수준의 정확도를 갖고 있다는 것을 나타냅니다. 일반적으로 MSE 값은 0에 가까워야 하며, 낮은 값일수록 더 나은 성능을 보입니다.

R-제곱 (R2): 0.4652924370503557
R-제곱은 종속 변수의 분산 중 독립 변수로부터 예측 가능한 비율을 측정합니다. 1은 완벽한 예측을 나타내며, 0은 선형 관계가 없음을 나타냅니다. 이 경우 R-제곱 값은 0.4652924370503557으로, 모델에 사용된 독립 변수로 타겟 변수의 약 46.53%의 분산을 설명할 수 있다는 것을 나타냅니다. 이는 모델이 변수 간의 상관 관계의 중요한 부분을 포착할 수 있지만 전부는 아니라는 것을 시사합니다.

중요한 그래프 몇 가지를 살펴보겠습니다:

# 잔차 그래프
residuals = y_test - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.axhline(y=0, color='red', linestyle='--')
plt.show()

# 예측 대 실제 그래프
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Predicted vs Actual Values')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=4)
plt.show()

사용하기 statsmodels

파이썬의 Statsmodels 라이브러리는 통계 분석을 위한 강력한 도구입니다. 선형 회귀, 시계열 분석, 비모수 방법 등 다양한 통계 모델과 테스트를 제공합니다.

다중 선형 회귀의 맥락에서 statsmodels는 데이터에 선형 모델을 적합시키고, 모델에 대한 다양한 통계 테스트와 분석을 수행하는 데 사용할 수 있습니다. 이는 독립 변수와 종속 변수 간의 관계를 이해하고 모델을 기반으로 예측을 수행하는 데 특히 유용할 수 있습니다.

import statsmodels.api as sm

# 모델에 상수를 추가하기
X_train_sm = sm.add_constant(X_train)
model_sm = sm.OLS(y_train, X_train_sm).fit()
print(model_sm.summary())

# 잔차에 대한 Q-Q 플롯
sm.qqplot(model_sm.resid, line='s')
plt.title('Q-Q Plot of Residuals')
plt.show()

출력:

==============================================================================
Dep. Variable:          MedHouseValue   R-squared:                       0.485
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     5173.
Date:                Fri, 17 Jan 2025   Prob (F-statistic):               0.00
Time:                        09:40:54   Log-Likelihood:                -20354.
No. Observations:               16512   AIC:                         4.072e+04
Df Residuals:                   16508   BIC:                         4.075e+04
Df Model:                           3                                        
Covariance Type:            nonrobust                                        
==============================================================================
                coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0679      0.006    320.074      0.000       2.055       2.081
x1             0.8300      0.007    121.245      0.000       0.817       0.843
x2            -0.1000      0.007    -14.070      0.000      -0.114      -0.086
x3            -0.0397      0.006     -6.855      0.000      -0.051      -0.028
==============================================================================
Omnibus:                     3981.290   Durbin-Watson:                   1.983
Prob(Omnibus):                  0.000   Jarque-Bera (JB):            11583.284
Skew:                           1.260   Prob(JB):                         0.00
Kurtosis:                       6.239   Cond. No.                         1.42
==============================================================================

위 표의 요약은 다음과 같습니다:

모델 요약

이 모델은 일반 최소제곱법 회귀 모델로, 선형 회귀 모델의 일종입니다. 종속 변수는 MedHouseValue이며, 모델의 R-제곱 값은 0.485로, MedHouseValue의 변동 중 약 48.5%를 독립 변수들이 설명할 수 있음을 나타냅니다. 조정된 R-제곱 값은 0.484로, R-제곱의 수정 버전으로, 추가 독립 변수를 포함할 때 모델에 패널티를 부과합니다.

모델 적합도

이 모델은 최소제곱법을 사용하여 적합시켰으며, F-통계량은 5173으로, 모델이 적합하다는 것을 의미합니다. 관측된 F-통계량만큼 극단적인 값이 나올 확률은 대략 0으로, 이는 모델이 통계적으로 유의함을 시사합니다.

모델 계수

모델 계수는 다음과 같습니다:

• 상수항은 2.0679로, 모든 독립 변수가 0일 때 예상되는 MedHouseValue는 대략 2.0679입니다.
• x1(이 경우 MedInc)의 계수는 0.8300으로, MedInc가 한 단위 증가할 때, 다른 모든 독립 변수들이 일정하다고 가정하면 예상되는 MedHouseValue는 대략 0.83만큼 증가합니다.
• x2의 계수(이 경우 AveRooms)는 -0.1000으로, x2가 1단위 증가할 때 예측된 MedHouseValue가 약 0.10 단위 감소함을 나타내며, 모든 다른 독립 변수가 일정하게 유지된다고 가정합니다.
• x3의 계수(이 경우 AveOccup)는 -0.0397로, x3가 1단위 증가할 때 예측된 MedHouseValue가 약 0.04 단위 감소함을 나타내며, 모든 다른 독립 변수가 일정하게 유지된다고 가정합니다.

모델 진단

모델 진단 결과는 다음과 같습니다:

• 옴니버스 테스트 통계량은 3981.290으로, 잔차가 정규 분포를 따르지 않음을 나타냅니다.
• 더빈-왓슨 통계량은 1.983으로, 잔차에 유의미한 자기 상관이 없음을 나타냅니다.
• 자크-베라 테스트 통계량은 11583.284로, 잔차가 정규 분포를 따르지 않음을 나타냅니다.
• 잔차의 비대칭도는 1.260으로, 잔차가 오른쪽으로 치우쳐 있음을 나타냅니다.
• 잔차의 첨도는 6.239로, 잔차가 레프토쿠르틱임을 나타내며(즉, 정규 분포보다 더 높은 피크와 더 두꺼운 꼬리를 가집니다).
• 조건 수는 1.42로, 모델이 데이터의 작은 변화에 민감하지 않음을 나타냅니다.

다중 공선성 처리

다중공선성은 다중 선형 회귀에서 흔히 발생하는 문제로, 두 개 이상의 독립 변수가 서로 높은 상관관계를 가지는 경우를 말합니다. 이는 계수의 불안정하고 신뢰할 수 없는 추정을 초래할 수 있습니다.

다중공선성을 탐지하고 처리하기 위해 분산 팽창 계수(Variance Inflation Factor, VIF)를 사용할 수 있습니다. VIF는 예측 변수가 상관관계가 있을 때 추정된 회귀 계수의 분산이 얼마나 증가하는지를 측정합니다. VIF가 1이면 특정 예측 변수와 다른 예측 변수 간에 상관관계가 없음을 의미합니다. VIF 값이 5 또는 10을 초과하면 문제적인 수준의 공선성을 나타냅니다.

아래 코드 블록에서는 모델의 각 독립 변수에 대한 VIF를 계산해 보겠습니다. VIF 값이 5를 초과하는 경우, 해당 변수를 모델에서 제거하는 것을 고려해야 합니다.

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif_data = pd.DataFrame()
vif_data['Feature'] = selected_features
vif_data['VIF'] = [variance_inflation_factor(X_scaled, i) for i in range(X_scaled.shape[1])]
print(vif_data)

# VIF 값에 대한 막대 그래프
vif_data.plot(kind='bar', x='Feature', y='VIF', legend=False)
plt.title('Variance Inflation Factor (VIF) by Feature')
plt.ylabel('VIF Value')
plt.show()

출력:

   Feature       VIF
0    MedInc  1.120166
1  AveRooms  1.119797
2  AveOccup  1.000488

각 특징의 VIF 값은 다음과 같습니다:

• MedInc: VIF 값은 1.120166으로, 다른 독립 변수와의 상관관계가 매우 낮음을 나타냅니다. 이는 MedInc가 모델의 다른 독립 변수와 높은 상관관계를 가지지 않음을 시사합니다.
• AveRooms: VIF 값은 1.119797로, 다른 독립 변수와의 상관관계가 매우 낮음을 나타냅니다. 이는 AveRooms가 모델의 다른 독립 변수와 높은 상관관계를 가지지 않음을 시사합니다.
• AveOccup: VIF 값이 1.000488으로, 다른 독립 변수들과 상관 관계가 없음을 나타냅니다. 이는 AveOccup이 모델의 다른 독립 변수들과 상관 관계가 없다는 것을 시사합니다.

일반적으로, 이러한 VIF 값은 모두 5 미만으로, 모델의 독립 변수들 간에 유의한 다중공선성이 없다는 것을 나타냅니다. 이는 모델이 안정적이고 신뢰할 수 있으며, 독립 변수의 계수가 다중공선성에 의해 유의미하게 영향을 받지 않음을 시사합니다.

교차 검증 기법

교차 검증은 머신 러닝 모델의 성능을 평가하는 기술입니다. 한정된 데이터 샘플이 있는 경우 모델을 평가하는 데 사용되는 재표본 추출 절차입니다. 이 절차에는 주어진 데이터 샘플을 나눌 그룹의 수를 나타내는 k라는 단일 매개 변수가 있습니다. 따라서 이 절차는 종종 k-겹 교차 검증이라고 불립니다.

from sklearn.model_selection import cross_val_score
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='r2')
print("Cross-Validation Scores:", scores)
print("Mean CV R^2:", scores.mean())

# 교차 검증 점수에 대한 라인 플롯
plt.plot(range(1, 6), scores, marker='o', linestyle='--')
plt.xlabel('Fold')
plt.ylabel('R-squared')
plt.title('Cross-Validation R-squared Scores')
plt.show()

출력:

Cross-Validation Scores: [0.42854821 0.37096545 0.46910866 0.31191043 0.51269138]
Mean CV R^2: 0.41864482644003276

교차 검증 점수는 모델이 보이지 않는 데이터에서 얼마나 잘 수행하는지를 나타냅니다. 점수는 0.31191043에서 0.51269138까지 변동하며, 모델의 성능이 서로 다른 폴드 간에 다양하게 나타납니다. 높은 점수는 더 나은 성능을 나타냅니다.

평균 CV R^2 점수는 0.41864482644003276이며, 이는 평균적으로 모델이 대상 변수의 분산 중 약 41.86%를 설명한다는 것을 나타냅니다. 이는 중간 수준의 설명력으로, 모델이 대상 변수를 예측하는 데 어느 정도 효과적이지만 추가적인 개선이나 정제가 필요할 수 있음을 나타냅니다.

이 점수들은 모델의 일반화 가능성을 평가하고 개선할 수 있는 잠재적인 영역을 식별하는 데 사용될 수 있습니다.

특성 선택 방법

재귀적 특성 제거 방법은 특성 선택 기술로, 지정된 특성 수에 도달할 때까지 가장 중요하지 않은 특성을 재귀적으로 제거합니다. 이 방법은 많은 수의 특성을 처리하고 가장 유용한 특성들의 하위 집합을 선택하는 경우에 특히 유용합니다.

제공된 코드에서는 먼저 sklearn.feature_selection에서 RFE 클래스를 가져옵니다. 그런 다음 특정 추정기(이 경우 LinearRegression)로 RFE의 인스턴스를 생성하고 n_features_to_select를 2로 설정하여 상위 2개의 특성을 선택하고자 합니다.

다음으로, 우리는 스케일 조정된 특성 X_scaled와 대상 변수 y에 RFE 객체를 맞춥니다. RFE 객체의 support_ 속성은 선택된 특성을 나타내는 부울 마스크를 반환합니다.

특성 순위를 시각화하기 위해 특성 이름과 해당 순위를 포함하는 DataFrame을 생성합니다. RFE 객체의 ranking_ 속성은 각 특성의 순위를 반환하며, 낮은 값일수록 중요한 특성을 나타냅니다. 그런 다음 특성 순위 값에 따라 정렬된 특성 순위 막대 차트를 플롯합니다. 이 플롯을 통해 모델에서 각 특성의 상대적 중요성을 이해할 수 있습니다.

from sklearn.feature_selection import RFE
rfe = RFE(estimator=LinearRegression(), n_features_to_select=3)
rfe.fit(X_scaled, y)
print("Selected Features:", rfe.support_)

# 특성 순위 막대 차트
feature_ranking = pd.DataFrame({
   'Feature': selected_features,
   'Ranking': rfe.ranking_
})
feature_ranking.sort_values(by='Ranking').plot(kind='bar', x='Feature', y='Ranking', legend=False)
plt.title('Feature Ranking (Lower is Better)')
plt.ylabel('Ranking')
plt.show()

출력:

Selected Features: [ True  True False]

위의 차트를 기반으로, 가장 적합한 2개의 특성은 MedInc와 AveRooms입니다. 이는 모델의 출력에서도 확인할 수 있으며, 종속 변수 MedHouseValue가 주로 MedInc와 AveRooms에 의존함을 나타냅니다.

자주 묻는 질문

파이썬에서 다중 선형 회귀를 어떻게 구현하나요?

파이썬에서 다중 선형 회귀를 구현하려면 statsmodels 또는 scikit-learn과 같은 라이브러리를 사용할 수 있습니다. 다음은 scikit-learn을 사용한 간단한 개요입니다:

from sklearn.linear_model import LinearRegression
import numpy as np

# 예제 데이터
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # 예측 변수
y = np.array([5, 7, 9, 11])  # 목표 변수

# 모델 생성 및 적합
model = LinearRegression()
model.fit(X, y)

# 계수 및 절편 가져오기
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# 예측 생성
predictions = model.predict(X)
print("Predictions:", predictions)

이를 통해 모델을 적합하고 계수를 얻고 예측을 수행하는 방법을 보여줍니다.

파이썬에서 다중 선형 회귀의 가정은 무엇인가요?

다중 선형 회귀는 유효한 결과를 보장하기 위해 여러 가정에 의존합니다:

1. 선형성: 예측 변수와 목표 변수 간의 관계가 선형이어야 합니다.
2. 독립성: 관측치는 서로 독립적이어야 합니다.
3. 등분산성: 잔차(오차)의 분산이 독립 변수의 모든 수준에서 일정해야 합니다.
4. 잔차의 정규성: 잔차는 정규 분포되어 있어야 합니다.
5. 다중공선성이 없음: 독립 변수들은 서로 높은 상관 관계가 없습니다.

잔차 플롯, 분산팽창요인(VIF), 또는 통계 검정과 같은 도구를 사용하여 이러한 가정을 테스트할 수 있습니다.

파이썬에서 다중 회귀 결과를 해석하는 방법은 무엇입니까?

회귀 결과에서 중요한 지표는 다음과 같습니다:

1. 계수 (coef_): 다른 변수를 고정시킨 채 해당 예측변수의 단위 변화에 따른 목표 변수의 변화를 나타냅니다.

예: X1에 대한 계수가 2이면 다른 변수를 고정시킨 채 X1이 1단위 증가할 때 목표 변수가 2씩 증가한다는 것을 의미합니다.

2.절편 (intercept_): 모든 예측변수가 0일 때 목표 변수의 예측값을 나타냅니다.

3.R-제곱: 예측변수들에 의해 설명되는 목표 변수의 분산 비율을 설명합니다.

예: R^2 값이 0.85인 경우 목표 변수의 변동성 중 85%가 모델에 의해 설명됩니다.

4.P-값 (statsmodels에서): 예측변수의 통계적 유의성을 평가합니다. 일반적으로 p-값이 0.05보다 작으면 예측변수가 유의미하다는 것을 나타냅니다.

파이썬에서 간단한 선형 회귀와 다중 선형 회귀의 차이는 무엇인가요?

결론

이 포괄적인 튜토리얼에서는 캘리포니아 주택 데이터셋을 사용하여 다중 선형 회귀를 구현하는 방법을 배웠습니다. 다중공선성, 교차 검증, 특성 선택 및 정규화와 같이 중요한 측면을 다루면서 각 개념을 철저히 이해했습니다. 잔차, 특성 중요도 및 전체 모델 성능을 보여주기 위해 시각화를 활용하는 방법도 배웠습니다. 이제 파이썬에서 견고한 회귀 모델을 쉽게 구축하고 이러한 기술을 실제 문제에 적용할 수 있습니다.