מפות מאורגנות עצמית: מדריך אינטואיטיבי עם דוגמאות בפייתון

הגדרת הסביבה עבור SOM

לפני בניית ה-SOM, אנו צריכים להכין את הסביבה עם החבילות הנדרשות. 

התקנת ספריות Python 

אנו זקוקים לחבילות הללו: 

• MiniSom היא כלי Python מבוסס NumPy שמייצר ומאמן SOMs. 
• NumPy משמשת לגישה לפונקציות מתמטיות כמו חלוקת מערכים, קבלת ערכים ייחודיים וכו'. 
• matplotlib משמשת לציור גרפים ומדדים שונים כדי להמחיש את הנתונים. 
• חבילת datasets מsklearn משמשת לייבוא נתונים עליהם נשתמש ב-SOM. 
• חבילת MinMaxScaler מsklearn מנרמלת את הנתונים. 

קטע הקוד הבא מייבא את החבילות הללו: 

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler

הכנת הנתונים

במדריך זה, אנו משתמשים ב-MiniSom כדי לבנות SOM ולאחר מכן לאמן אותו על ה נתוני IRIS. נתונים אלו מורכבים מ-3 קטגוריות של צמחים מסוג איריס. לכל קטגוריה יש 50 דוגמאות. כדי להכין את הנתונים, אנו עוקבים אחרי הצעדים הבאים: 

• מייבאים את נתוני האיריס מ-sklearn, 
• מוציאים את וקטורי הנתונים ואת הסקלרים המיועדים. 
• נרמל את וקטורי הנתונים. במדריך זה, אנו משתמשים ב MinMaxScaler מ-scikit-learn. 
• להכריז על קבוצת תוויות לכל אחת משלוש הקטגוריות של צמחי איריס. 

הקוד הבא מממש את הצעדים הללו: 

dataset_iris = datasets.load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target
data_iris_normalized = MinMaxScaler().fit_transform(data_iris)
labels_iris = {1:'1', 2:'2', 3:'3'}
data = data_iris_normalized
target = target_iris

מימוש מפות מאורגנות עצמית (SOM) בפייתון

כדי לממש SOM בפייתון, אנו מגדירים ומאתחלים את הרשת לפני האימון שלה על מערך הנתונים. לאחר מכן נוכל לדמיין את הנוירונים המאומנים ואת מערך הנתונים הקבוצתי. 

הגדרת רשת ה-SOM

כפי שהוסבר קודם, SOM הוא רשת של נוירונים. באמצעות MiniSom, אנו יכולים ליצור רשתות בגובה של 2. ממדי ה-X וה-Y של הרשת הם מספר הנוירונים לאורך כל ציר. כדי להגדיר את רשת ה-SOM, אנו צריכים גם להגדיר:

• את ממדי ה-X וה-Y של הרשת
• מספר משתני הקלט – זהו מספר שורות הנתונים.

הכריז על פרמטרים אלה constants בפייתון:

SOM_X_AXIS_NODES  = 8
SOM_Y_AXIS_NODES  = 8
SOM_N_VARIABLES  = data.shape[1]

הקוד לדוגמה למטה מדגים כיצד להכריז על הרשת באמצעות MiniSom:

som = MiniSom(SOM_X_AXIS_NODES, SOM_Y_AXIS_NODES, SOM_N_VARIABLES)

שני הפרמטרים הראשונים הם מספר הנוירונים לאורך צירי ה-X וה-Y, והפרמטר השלישי הוא מספר המשתנים.

אנו מצהירים על פרמטרים אחרים והיפרפרמטרים בעת יצירת רשת SOM. נבהיר את אלה מאוחר יותר במדריך. לעכשיו, הצהירו על הפרמטרים הללו כפי שמוצג למטה:

ALPHA = 0.5
DECAY_FUNC = 'linear_decay_to_zero'
SIGMA0 = 1.5
SIGMA_DECAY_FUNC = 'linear_decay_to_one'
NEIGHBORHOOD_FUNC = 'triangle'
DISTANCE_FUNC = 'euclidean'
TOPOLOGY = 'rectangular'
RANDOM_SEED = 123

צור SOM באמצעות הפרמטרים הללו:

som = MiniSom(
        SOM_X_AXIS_NODES,
        SOM_Y_AXIS_NODES,
        SOM_N_VARIABLES,
        sigma=SIGMA0,
        learning_rate=ALPHA,
        neighborhood_function=NEIGHBORHOOD_FUNC,
        activation_distance=DISTANCE_FUNC,
        topology=TOPOLOGY,
        sigma_decay_function = SIGMA_DECAY_FUNC,
        decay_function = DECAY_FUNC,
        random_seed=RANDOM_SEED,
        )

אתחול הנוירונים

הפקודה למעלה יוצרת SOM עם משקלים אקראיים עבור כל הנוירונים. אתחול הנוירונים עם משקלים שנלקחו מהנתונים (במקום מספרים אקראיים) יכול להפוך את תהליך ההדרכה ליעיל יותר.

כשמשתמשים ב-MiniSom כדי ליצור מפה עצמית-מאורגנת (SOM), יש שתי דרכים לאתחל את משקלי הנוירונים בהתבסס על הנתונים:

• אתחול אקראי: משקלי הנוירונים הראשוניים נמשכים באופן אקראי מהנתוני הקלט. אנו עושים זאת על ידי יישום הפונקציה .random_weights_init() על ה-SOM. 
• אתחול PCA: אתחול ניתוח רכיבים עיקריים (PCA) משתמש ברכיבים העיקריים של נתוני הקלט כדי לאתחל את המשקלים. משקלי הנוירונים הראשוניים מכסים את שני הרכיבים העיקריים הראשונים. זה לרוב מוביל להתכנסות מהירה יותר.

במדריך הזה, אנו משתמשים בהתחלת PCA. כדי להפעיל את התחלת PCA על משקולות ה-SOM, השתמש בפונקציה .pca_weights_init() כפי שמוצג למטה:

som.pca_weights_init(data)

אימון ה-SOM

תהליך האימון מעדכן את משקולות ה-SOM כדי למזער את המרחק בין הנוירונים לנקודות הנתונים.

למטה, אנו מסבירים את תהליך האימון החזרתי:

• התחלה: וקטורי המשקל של כל הנוירונים מתחילים, בדרך כלל עם ערכים אקראיים. כמו כן, ניתן להתחיל את המשקולות על ידי דגימה מהתפלגות הנתונים הקלטיים.
• בחירת קלט: וקטור קלט נבחר (באופן אקראי) מתוך קבוצת הנתונים לאימון.
• זיהוי BMU: הנוירון עם וקטור המשקל הקרוב ביותר לוקטור הקלט מזוהה כ-BMU.
• עדכון שכונה: ה-BMU והנוירונים השכנים שלו מעדכנים את וקטורי המשקל שלהם. שיעור הלמידה ופונקציית השכונה קובעים אילו נוירונים מעודכנים ובאיזה מידה. בשלב האיטרציה t, בהתחשב בוקטור הקלט x, וקטור המשקל של נוירון i הוא w_i, שיעור הלמידה (t), ופונקציית השכונה h_bi (פונקציה זו מכמתת את מידת העדכון עבור הנוירון i בהתחשב בנוירון ה-BMU b), נוסחת עדכון המשקל עבור נוירון i מתבטאת כך:
• שיעור דעיכת קצב הלמידה ורדיוס השכונה: הן קצב הלמידה והן רדיוס השכונה פוחתים עם הזמן. באיטרציות המוקדמות, תהליך האימון מבצע התאמות גדולות יותר על פני שכונה רחבה יותר. איטרציות מאוחרות יותר מסייעות לכוונן את המשקלים על ידי ביצוע שינויים קטנים יותר במשקלי הנוירונים הסמוכים. זה מאפשר למפה להתייצב ולהתכנס. 

כדי לאמן את ה-SOM, אנו מציגים למודל את נתוני הקלט. אנו יכולים לבחור אחת משתי גישות כדי לעשות זאת: 

• בחר דגימות באופן אקראי מנתוני הקלט. הפונקציה .train_random() מיישמת טכניקה זו. 
• הרץ באופן רציף דרך הווקטורים בנתוני הקלט. זה מתבצע באמצעות פונקציית .train_batch()  

הפונקציות הללו מקבלות את נתוני הקלט ואת מספר האיטרציות כפרמטרים. במדריך זה, אנו משתמשים בפונקציית .train_random() הכרז על מספר האיטרציות כקבוע והעבר אותו לפונקציית האימון: 

N_ITERATIONS = 5000
som.train_random(data, N_ITERATIONS, verbose=True)  

לאחר הרצת הסקריפט וסיום האימון, תופיע הודעה עם שגיאת הקואנטיזציה:

quantization error: 0.05357240680504421 

שגיאת הקוונטיזציה מצביעה על כמות המידע שאבדה כאשר ה-SOM קוונטיזציה (מפחיתה את ממדי) הנתונים. שגיאת קוונטיזציה גדולה מציינת מרחק גדול יותר בין הנוירונים לנקודות הנתונים. זה גם אומר שהקיבוץ פחות מהימן.

הדמיית נוירוני SOM

עכשיו יש לנו מודל SOM מאומן. כדי להמחיש אותו, אנו משתמשים במפת מרחקים (המכונה גם מטריצת U). מפת המרחקים מציגה את הנוירונים של ה-SOM כרשת של תאים. הצבע של כל תא מייצג את המרחק שלו מהנוירונים השכנים.

מפת המרחקים היא רשת באותן ממדים כמו ה-SOM. כל תא במפת המרחקים הוא הסכום הנורמלי של (מרחקים אוקלידיים) בין נוירון לשכנים שלו.

גש אל SOM distance map באמצעות הפונקציה .distance_map(). כדי לייצר את המטריצה U, אנו עוקבים אחרי הצעדים הבאים:

• השתמש בpyplot כדי ליצור דמות עם אותן מידות כמו ה-SOM. בדוגמה זו, המידות הן 8×8.
• צייר את מפת המרחקים באמצעות matplotlib באמצעות הפונקציה .pcolor() בדוגמה זו, אנו משתמשים בgist_yarg כמערכת צבעים.
• הצג את הcolorbar, אינדקס הממפה צבעים שונים לערכים סקלריים שונים. במקרה זה, מכיוון שהמרחקים מנורמלים, ערכי המרחק הסקלריים נעים בין 0 ל-1. 

הקוד למטה מיישם את הצעדים הללו: 

# צור את הרשת
plt.figure(figsize=(8, 8))
#צייר את מפה המרחקים
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
# הצג את סרגל הצבעים
plt.colorbar()
plt.show()

בדוגמה זו, מטריצת ה-U משתמשת בסכמה צבעונית מונוטונית. ניתן להבין זאת באמצעות ההנחיות הללו:

• גוון בהיר מייצג נוירונים הצמודים זה לזה, וגוון כהה מייצג נוירונים המרוחקים אחד מהשני. 
• קבוצות של גוונים בהירים יכולות להתפרש כקלאסטרים. קשרים כהים בין הקלאסטרים יכולים להתפרש כגבולות בין הקלאסטרים.

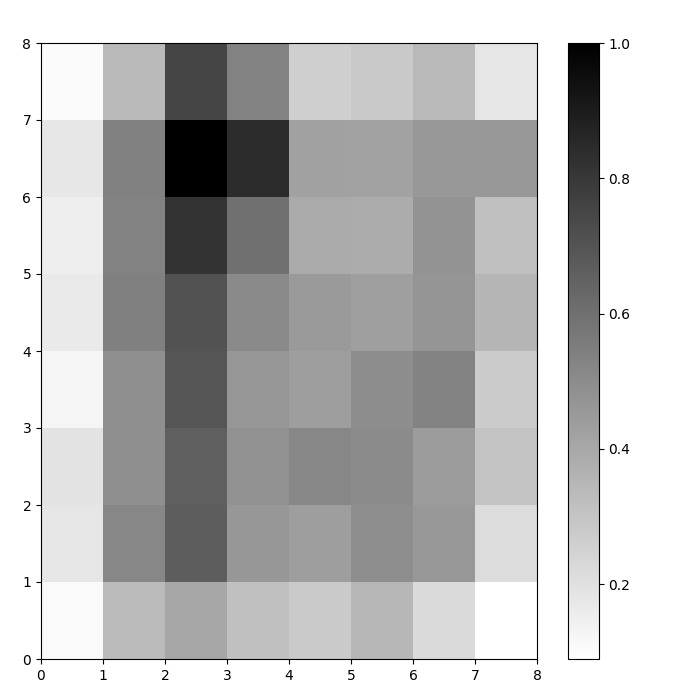
איור 1: מטריצת U של SOM מאומן על מערך הנתונים של איריס (תמונה מאת המחבר)

הערכת תוצאות הקלאסטרינג של SOM

האיור הקודם המחיש בצורה גרפית את הנוירונים של ה-SOM. בחלק זה, אנו מראים כיצד לדמיין כיצד ה-SOM קלאסטר את הנתונים.

זיהוי קלאסטרים

אנו מניחים סמנים על פני מטריצת U למעלה כדי לציין לאיזו כיתה של צמח איריס מייצג כל תא (נוירון). כדי לעשות זאת:

• כפי שעשיתם קודם, צרו דמות של 8×8 בעזרת pyplot, ציירו את מפה המרחקים, והציגו את סרגל הצבעים. 
• ציינו מערך של שלושה סימני matplotlib, אחד עבור כל סוג של צמח איריס. 
• ציינו מערך של שלושה קודי צבע matplotlib, אחד עבור כל סוג של צמח איריס. 
• ציירו באופן איטרטיבי את הנוירון המנצח עבור כל נקודת נתונים:
• קבע את (קואורדינטות ה)נוירון המנצח עבור כל נקודת נתונים באמצעות הפונקציה .winner() .
• שרטט את מיקום כל נוירון מנצח במרכז כל תא על הרשת. w[0] ו w[1] נותנים את קואורדינטות ה-X וה-Y של הנוירון, בהתאמה. ערך של 0.5 מתווסף לכל קואורדינטה כדי לשרטט אותו במרכז התא.

הקוד להלן מראה כיצד לעשות זאת:

# שרטט את מפת המרחק
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg') 
plt.colorbar()
# צור את הסימנים והצבעים לכל קבוצה
markers = ['o', 'x', '^']
colors = ['C0', 'C1', 'C2']
# שרטט את הנוירון המנצח עבור כל נקודת נתונים
for count, datapoint in enumerate(data):
    # קבל את המנצח
    w = som.winner(datapoint)  
    # הנח סימן על המיקום המנצח עבור נקודת נתונים לדוגמה
    plt.plot(w[0]+.5, w[1]+.5, markers[target[count]-1], markerfacecolor='None',
             markeredgecolor=colors[target[count]-1], markersize=12, markeredgewidth=2)
plt.show()

התמונה الناتחת מוצגת למטה:

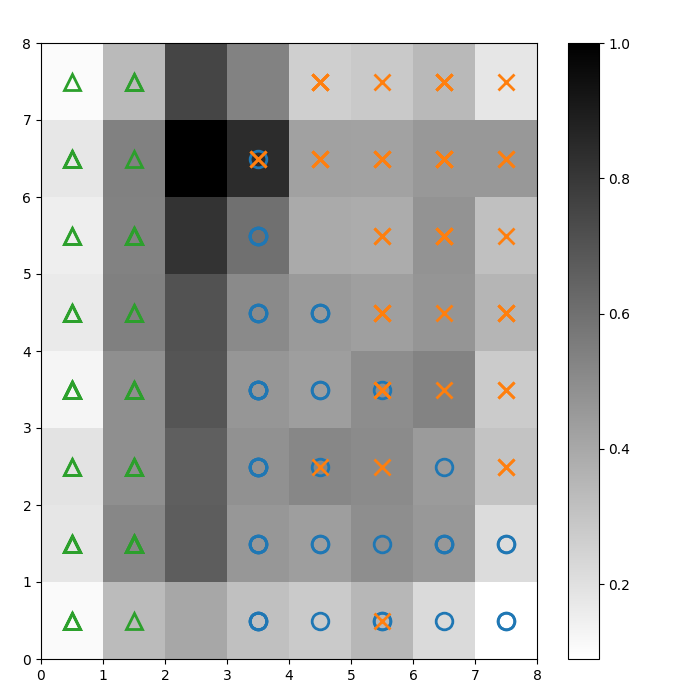
איור 2: מטריצת U עם סימני כיתה (תמונה מאת המחבר)

בהתבסס על מסמכי מערכת הנתונים של איריס, “כיתה אחת ניתנת להפרדה ליניארית משתי האחרות; האחרונות אינן ניתנות להפרדה ליניארית אחת מהשנייה”. במטריצת U למעלה, שלוש הכיתות הללו מיוצגות על ידי שלושה סימנים – משולש, עיגול, ו-X.

שימו לב שאין גבול ברור בין העיגולים הכחולים ל-Xים הכתומים. יתר על כן, שתי כיתות משולבות על אותו נוירון בהרבה תאים. זה אומר שהנוירון במרחק שווה משתי הכיתות.

ויזואליזציה של תוצאת הקלסטרינג

מודל SOM הוא מודל של אשכולות. נקודות נתונים דומות מתמפות לאותו נוירון. נקודות נתונים מאותה קטגוריה מתמפות לאשכול של נוירונים סמוכים. אנו מציגים את כל נקודות הנתונים על רשת ה-SOM כדי ללמוד טוב יותר את התנהגות האשכולות.

השלבים הבאים מתארים כיצד ליצור את גרף הפיזור הזה:

• קבל את הקואורדינטות X ו-Y של הנוירון המנצח עבור כל נקודת נתונים.
• הצג את מפת המרחקים, כפי שעשינו עבור איור 1.
• השתמש ב-plt.scatter() כדי ליצור גרף פיזור של כל הנוירונים המנצחים עבור כל נקודת נתונים. הוסף סטייה אקראית לכל נקודה כדי להימנע מהצטברויות בין נקודות נתונים באותו תא.

אנו מיישמים את הצעדים האלה בקוד למטה: 

# קבל את הקואורדינטות X ו-Y של הנוירון המנצח עבור כל נקודת נתוניםw_x, w_y = zip(*[som.winner(d) for d in data])
w_x = np.array(w_x)
w_y = np.array(w_y)
# צייר את מפה המרחקים
plt.figure(figsize=(8, 8))
plt.pcolor(som.distance_map().T, cmap='gist_yarg', alpha=.2)
plt.colorbar()
# צור גרף פיזור של כל הנוירונים המנצחים עבור כל נקודת נתונים
# הוסף סטייה אקראית לכל נקודה כדי להימנע מהצטברויות
for c in np.unique(target):
    idx_target = target==c
    plt.scatter(w_x[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                w_y[idx_target]+.5+(np.random.rand(np.sum(idx_target))-.5)*.8,
                s=50, 
                c=colors[c-1], 
                label=labels_iris[c+1]
                )
plt.legend(loc='upper right')
plt.grid()
plt.show()

הגרף הבא מציג את גרף הפיזור הפלט:

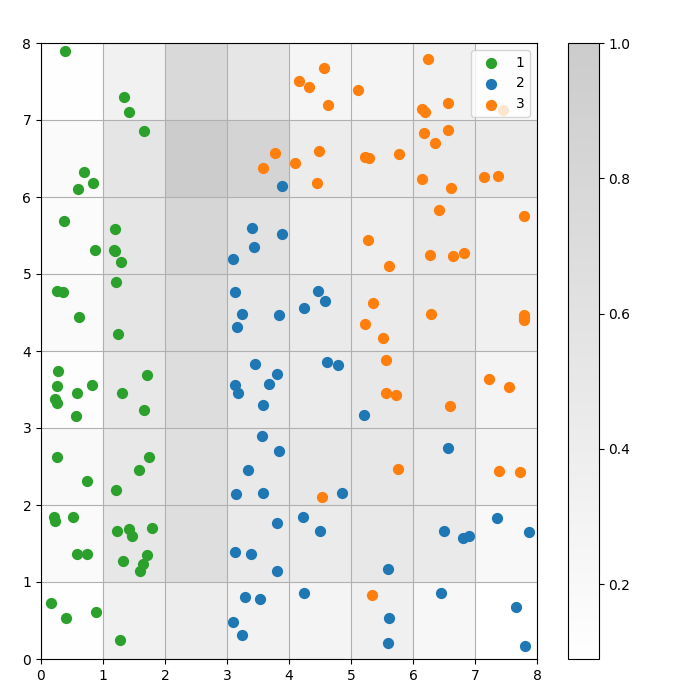איור 3: גרף פיזור של נקודות נתונים בתוך תאים (תמונה מאת המחבר)

בגרף הפיזור למעלה, שימו לב ש: 

• חלק מהתאים מכילים גם נקודות כחולות וגם נקודות כתומות. 
• הנקודות הירוקות מופרדות בבירור משאר הנתונים, אך הנקודות הכחולות והנקודות הכתומות אינן מופרדות בצורה נקייה. 
• התצפיות לעיל תואמות לעובדה שרק אחד מתוך שלושת הקלאסטרים במערך הנתונים Iris יש לו גבול ברור.
• באיור 1, צמתים כהים בין הקלאסטרים (שניתן לפרש אותם כגבולות בין קלאסטרים) תואמים לתאים ריקים בגרף הפיזור.

אתה יכול לגשת ולהריץ את הקוד המלא במחברת DataLab זו.

כיוונון מודל SOM

החלקים הקודמים הראו כיצד ליצור ולאמן מודל SOM וכיצד ללמוד את התוצאות בצורה ויזואלית. בחלק זה, נדון כיצד לכוון את הביצועים של מודלי SOM.

מפתחות היפר-פרמטרים לכיוון

כמו בכל מודל למידת מכונה, ההיפרפרמטרים משפיעים באופן משמעותי על ביצועי המודל.

כמה מההיפרפרמטרים החשובים באימון SOMs הם:

• גודל הרשת קובע את גודל המפה. מספר הנוירונים במפה עם גודל רשת של AxB הוא A*B.
• הקצב הלמידה קובע כמה משקלים משתנים בכל חזרה. אנו קובעים את קצב הלמידה ההתחלתי, והוא פוחת עם הזמן בהתאם לפונקציית ההתמוטטות.
• הפונקציית ההתמוטטות קובעת את המידה שבה קצב הלמידה פוחת בכל חזרה שלאחר מכן.
• הפונקציית השכונה היא פונקציה מתמטית המפרטת אילו נוירונים יש להתחשב כ"שכנים" של ה-BMU.
• ה סטיית התקן מפרטת את התפשטות פונקציית השכונה. לדוגמה, פונקציית שכונה גאוסיאנית עם סטיית תקן גבוהה תהיה לה שכונה רחבה יותר מאשר אותה פונקציה עם סטיית תקן נמוכה יותר. אנו קובעים את סטיית התקן ההתחלתית, אשר פוחתת עם הזמן בהתאם לפונקציית דעיכת הסיגמה.
• הפונקציית סיגמה דה-קיי שולטת בכמה הסטיית התקן מצטמצמת בכל חזרה עוקבת. 
• מספר החזרות האימון קובע כמה פעמים המשקלים מעודכנים. בכל חזרת אימון, משקלי הנוירון מעודכנים פעם אחת. 
• הפונקציית מרחק היא פונקציה מתמטית שמחשבת את המרחק בין נוירונים לנקודות נתונים. 
• הטופולוגיה קובעת את פריסת המבנה של הרשת. הנוירונים ברשת יכולים להיות מסודרים בתבנית מלבנית או היקסגונלית. 

בפרק הבא, נדון בהנחיות לקביעת הערכים של ההיפרפרמטרים הללו. 

השפעת כיוונון ההיפרפרמטרים

ערכי ההיפרפרמטרים צריכים להתקבל על סמך המודל והסט הנתונים. במידה מסוימת, קביעת ערכים אלה היא תהליך של ניסוי וטעייה. בחלק זה, אנו נותנים הנחיות לכיול כל היפרפרמטר. ליד כל היפרפרמטר, אנו מציינים (בסוגריים) את הקבועים המתאימים בפייתון שמשתמשים בהם בקוד לדוגמה.

• גודל הרשת (SOM_X_AXIS_NODES ו-SOM_X_AXIS_NODES): גודל הרשת תלוי בגודל של מערך הנתונים. הכלל הוא שכאשר יש מערך נתונים בגודל N, הרשת צריכה להכיל בערך 5*sqrt(N) נוירונים. לדוגמה, אם מערך הנתונים מכיל 150 דגימות, הרשת צריכה להכיל 5*sqrt(150) = בערך 61 נוירונים. במדריך הזה, מערך הנתונים של איריס מכיל 150 שורות ואנחנו משתמשים ברשת בגודל 8×8. 
• קצב הלמידה ההתחלתי (ALPHA): קצב גבוה יותר מאיץ את ההתכנסות, בעוד שקצבים נמוכים יותר משמשים להתאמות עדינות לאחר איטרציות מוקדמות. קצב הלמידה ההתחלתי צריך להיות גדול מספיק כדי לאפשר הסתגלות מהירה, אך לא כל כך גדול עד שיחרוג מערכי המשקל האופטימליים. במאמר זה, קצב הלמידה ההתחלתי הוא 0.5. 
• סטיית תקן התחלתית (SIGMA0): היא קובעת את הגודל או התפשטות ההתחלתית של השכונה. ערך גדול יותר לוקח בחשבון דפוסים גלובליים יותר. בדוגמה זו, אנו משתמשים בסטיית תקן התחלתית של 1.5. 
• עבור השיעור ההתפוררות (DECAY_FUNC) והשיעור של התפוררות סיגמה (SIGMA_DECAY_FUNC), אנו יכולים לבחור מתוך אחד משלושה סוגים של פונקציות התפוררות: 
• דעיכת הפוכה : פונקציה זו מתאימה אם לנתונים יש דפוסים גלובליים ומקומיים. במקרים כאלה, אנו זקוקים לשלב ארוך יותר של למידה רחבה לפני שנמוקד בדפוסים המקומיים.
• דעיכה ליניארית : זה טוב עבור מערכי נתונים שבהם אנו רוצים גודל שכונה עקבי ואחיד או הפחתת קצב הלמידה. זה שימושי אם הנתונים לא זקוקים להרבה כיוונון מדויק.
• דעיכה אסימפטוטית : פונקציה זו שימושית אם הנתונים מורכבים ובעלי ממדים גבוהים. במקרים כאלה, עדיף להקדיש יותר זמן לחקירה גלובלית לפני שעוברים בהדרגה לפרטים מדויקים יותר.
• פונקציית שכונה (NEIGHBORHOOD_FUNC): הבחירה המוגדרת של פונקציית השכונה היא הפונקציה הגאוסית. פונקציות אחרות, כפי שמוסבר למטה, גם משמשות. 
• גאוסית (ברירת מחדל): זו עקומה בצורת פעמון. המידה שבה נוירון מתעדכן פוחתת באופן חלקי ככל שהמרחק שלו מהנוירון המנצח גדל. היא מספקת מעבר חלק ורציף ושומרת על טופולוגיית הנתונים. היא מתאימה לרוב המטרות הכלליות בשל ההתנהגות היציבה והניבאת שלה.
• בועה: פונקציה זו יוצרת שכונה קבועה ברוחב. כל הנוירונים בתוך שכונה זו מתעדכנים באופן שווה, והנוירונים מחוץ לשכונה זו אינם מתעדכנים (לנקודת נתונים נתונה). זה זול יותר מבחינה חישובית ונוח יותר ליישום. זה שימושי למפות קטנות שבהן גבולות השכונה החדים אינם פוגעים בקיבוץ אפקטיבי. 
• כובע מקסיקני: יש לו אזור מרכזי חיובי מוקף באזור שלילי. הנוירונים הקרובים ל-BMU מתעדכנים כדי להתקרב לנקודת הנתונים, והנוירונים הרחוקים יותר מתעדכנים כדי להתרחק מנקודת הנתונים. טכניקה זו משפרת את הניגוד ומחדדת את התכונות במפה. מכיוון שהיא מדגישה קבוצות ברורות, היא אפקטיבית במשימות זיהוי תבניות שבהן נדרשת הפרדה ברורה של קבוצות.
• משולש: פונקציה זו מגדירה את גודל השכנות כמשולש, כאשר ה-BMU יש לו את ההשפעה הגדולה ביותר. זה פוחת באופן ליניארי עם המרחק מה-BMU. זה משמש לקיבוץ נתונים עם מעברים הדרגתיים בין קבוצות או תכונות, כמו נתוני תמונה, דיבור או סדרות זמן, כאשר נקודות נתונים שכנות צפויות לשתף תכונות דומות. 
• פונקציית מרחק (DISTANCE_FUNC): כדי למדוד את המרחק בין נוירונים ונקודות נתונים, אנו יכולים לבחור מתוך 4 שיטות:
• מרחק אוקלידי (בחירה ברירת מחדל): שימושי כאשר הנתונים רציפים, ורוצים למדוד מרחק בקו ישר. הוא מתאים לרוב המשימות הכלליות, במיוחד כאשר נקודות הנתונים מפוזרות באופן שווה ומקושרות מרחבית.
• מרחק קוסיני: בחירה טובה עבור טקסט או נתונים דלילים בממדים גבוהים שבהם הזווית בין הווקטורים חשובה יותר מהמגוון. זה שימושי להשוואת כיווניות בנתונים.
• מרחק מנהטן: אידיאלי כאשר נקודות הנתונים נמצאות על רשת או לattice (למשל, בלוקים עירוניים). זה פחות רגיש לערכים קיצוניים מאשר מרחק אוקלידי.
• מרחק צ'בישב: מתאים למצבים בהם תנועה יכולה להתקיים בכל כיוון (למשל, מרחקים בלוח שחמט). זה שימושי עבור מרחבים דיסקרטיים בהם אנו רוצים להעדיף את ההפרש המקסימלי בצירים.
• טופולוגיה (TOPOLOGY): ברשת, ניתן לסדר נוירונים במבנה משושה או מלבני: 
• מלבן (ברירת מחדל): לכל נוירון יש 4 שכנים מידיים. זו הבחירה הנכונה כאשר לנתונים אין קשר מרחבי ברור. זה גם פשוט יותר מבחינה חישובית.
• משושה: לכל נוירון יש 6 שכנים. זו האפשרות המועדפת אם לנתונים יש קשרים מרחביים שמיוצגים טוב יותר עם רשת משושה. זה המקרה עבור הפצות נתונים מעגליות או זוויתיות.
• מספר חזרות האימון (N_ITERATIONS): בעיקרון, זמני אימון ארוכים יותר מובילים לשגיאות נמוכות יותר וליישור טוב יותר של המשקלים עם נתוני הקלט. עם זאת, ביצועי המודל עולים באופן אסימפטוטי עם מספר החזרות. לכן, לאחר מספר מסוים של חזרות, העלייה בביצועים מהאינטראקציות הבאות היא רק שולית. קביעת מספר החזרות הנכון דורשת מעט ניסוי. במדריך זה, אנו מאמנים את המודל במשך 5000 חזרות. 

כדי לקבוע את התצורה הנכונה של היפרפרמטרים, אנו ממליצים לנסות אפשרויות שונות על תת-קבוצה קטנה יותר של הנתונים.

מסקנה

מפות מאורגנות עצמית הן כלי חזק עבור למידה לא מפוקחת. הן משמשות לקיבוץ, הפחתת ממדי, זיהוי אנומליות, ודימות נתונים. מכיוון שהן שומרות על המאפיינים הטופולוגיים של נתונים גבוהי ממד ומייצגות אותם על רשת נמוכה ממד, מפות מאורגנות עצמית מקלות על דימות והבנה של מערכות נתונים מורכבות.

מדריך זה דן בעקרונות הבסיסיים של מפות מאורגנות עצמית והראה כיצד לממש מפה כזו באמצעות ספריית מיניסום של פייתון. הוא גם הדגים כיצד לנתח את התוצאות באופן ויזואלי והסביר את ההיפרפרמטרים החשובים שמשתמשים בהם לאימון מפות מאורגנות עצמית ולשיפור ביצועיהן.